-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaA Flexible Approach for the Analysis of Rare Variants Allowing for a Mixture of Effects on Binary or Quantitative Traits
Multiple rare variants either within or across genes have been hypothesised to collectively influence complex human traits. The increasing availability of high throughput sequencing technologies offers the opportunity to study the effect of rare variants on these traits. However, appropriate and computationally efficient analytical methods are required to account for collections of rare variants that display a combination of protective, deleterious and null effects on the trait. We have developed a novel method for the analysis of rare genetic variation in a gene, region or pathway that, by simply aggregating summary statistics at each variant, can: (i) test for the presence of a mixture of effects on a trait; (ii) be applied to both binary and quantitative traits in population-based and family-based data; (iii) adjust for covariates to allow for non-genetic risk factors and; (iv) incorporate imputed genetic variation. In addition, for preliminary identification of promising genes, the method can be applied to association summary statistics, available from meta-analysis of published data, for example, without the need for individual level genotype data. Through simulation, we show that our method is immune to the presence of bi-directional effects, with no apparent loss in power across a range of different mixtures, and can achieve greater power than existing approaches as long as summary statistics at each variant are robust. We apply our method to investigate association of type-1 diabetes with imputed rare variants within genes in the major histocompatibility complex using genotype data from the Wellcome Trust Case Control Consortium.
Published in the journal: . PLoS Genet 9(8): e32767. doi:10.1371/journal.pgen.1003694
Category: Research Article
doi: https://doi.org/10.1371/journal.pgen.1003694Summary
Multiple rare variants either within or across genes have been hypothesised to collectively influence complex human traits. The increasing availability of high throughput sequencing technologies offers the opportunity to study the effect of rare variants on these traits. However, appropriate and computationally efficient analytical methods are required to account for collections of rare variants that display a combination of protective, deleterious and null effects on the trait. We have developed a novel method for the analysis of rare genetic variation in a gene, region or pathway that, by simply aggregating summary statistics at each variant, can: (i) test for the presence of a mixture of effects on a trait; (ii) be applied to both binary and quantitative traits in population-based and family-based data; (iii) adjust for covariates to allow for non-genetic risk factors and; (iv) incorporate imputed genetic variation. In addition, for preliminary identification of promising genes, the method can be applied to association summary statistics, available from meta-analysis of published data, for example, without the need for individual level genotype data. Through simulation, we show that our method is immune to the presence of bi-directional effects, with no apparent loss in power across a range of different mixtures, and can achieve greater power than existing approaches as long as summary statistics at each variant are robust. We apply our method to investigate association of type-1 diabetes with imputed rare variants within genes in the major histocompatibility complex using genotype data from the Wellcome Trust Case Control Consortium.
Introduction
Despite the recent successes of genome-wide association studies (GWAS), which can be well powered under the common disease, common variant hypothesis, the majority of the genetic component of many complex traits remains unexplained. For example, hundreds of common genetic variants, in at least 180 loci, have been associated with height in studies of up to more than 180,000 individuals. However, the individual effects of these variants are modest and their cumulative effect explains just over 10% of the phenotypic variation in height [1], [2], [3], [4]. Rare variants may play an important role in explaining the “missing heritability” of complex traits. Due to recent advances in high-throughput re-sequencing technology, it is becoming financially feasible to assay rare genetic variation in thousands of individuals on the scale of the whole-exome, or even the whole genome. Furthermore, with the availability of whole-genome re-sequencing reference panels, such as those made available through the 1000 Genomes Project [5], imputation allows the possibility to predict genotypes at rare variants not present on, or captured by, GWAS genotyping arrays. Therefore, we now have an exciting opportunity to explore a range of models that may help to explain the missing heritability of complex traits using rare genetic variation. One such model is that where a gene or region affects a complex trait as a consequence of the combined effects of its constituent rare variants. The effects at each rare variant can be either modest or highly penetrant, and can act to either increase or decrease the trait or disease risk.
Recently published methods for the analysis of multiple rare variants illustrate that power can be greatly increased by combining information in a joint analysis in comparison to studying individual variants one at a time [6], [7], [8], [9], [10], [11]. These so called “burden tests” are optimal when all variants have the same direction of effect. However, these variants may act individually to either increase or decrease trait values, or they may be neutral (i.e. no effect on the trait). Ideally, we wish to test for the presence of a mixture of increaser, decreaser and neutral effects at multiple rare variants on a complex binary or quantitative trait. Zelterman and Chen [12] describe tests of homogeneity against such central mixture alternatives for general sampling distributions that are based on the score function. These so called “C-alpha” tests are powerful for detecting the presence of central mixtures [13]. Neale et al. [14] proposed a C-alpha test for the analysis of sequence level data for association with binary (disease) traits based on binomially distributed measures of effect at each site. Their approach has the advantage of allowing for a mixture of risk, protective and neutral effects, but cannot explicitly be applied to quantitative traits, account for non-genetic risk factors as covariates, or allow for imputed variation. More recently, score-based variance component tests SKAT (sequence kernel association test) [15] and an optimized version (SKAT-O) [16] have been proposed for the detection of a mixture of effects which can be applied to both binary and quantitative traits and which can adjust for covariates. These tests have been shown to outperform burden tests and the Binomial C-alpha test in a wide range of scenarios.
Here, we introduce a C-alpha test for the analysis of rare genetic variation for association with both binary and quantitative traits based on normally distributed measures of effect at each site. Measures of effect at each site can be calculated from re-sequencing, array genotyping or imputed data or taken directly from summary measures of effect available, for example, from meta-analysis or published data. Our test assesses the evidence for a mixture of increaser, decreaser and neutral effects in a gene, region or pathway and can be applied to both population and family-based association studies and can adjust for covariates to allow for non-genetic risk factors, such as indicators of population stratification. We refer to our test as the Generalised C-alpha test. We report the results of simulations to investigate the power of our test to detect rare variant association with a quantitative trait, and compare performance with existing approaches.
The HLA class II genes in the major histocompatibility locus (MHC) play a major role in susceptibility to type-1 diabetes (T1D) [17], but common variants mapping to other genes in this region have also been implicated in the disease. Imputation into existing GWAS genotype data up to publicly available reference panels of sequence data can be used to identify novel and refined signals of association with common SNPs (MAF>1%) [18] and is feasible for the evaluation of rare variants [19]. We have used our Generalised C-alpha test to evaluate the evidence for rare variant association with T1D within genes in the MHC using GWAS genotype data from the Wellcome Trust Control Consortium (WTCCC) [20] imputed up to reference panels made available through the 1000 Genomes Project [5].
Materials and Methods
Generalised C-alpha Test
Consider a gene, region or pathway containing K variants, each with a minor allele frequency (MAF) less than a pre-defined threshold and assayed in a sample of individuals measured for a binary or a quantitative trait. Suppose that at each variant a normally distributed estimate of the effect of the minor allele on the trait of interest can be obtained. For example, in a case-control association study such an estimate may be the log allelic odds ratio obtained as a coefficient in a logistic regression; or in a quantitative trait association study, the estimate may be the per-allele increase in phenotypic value obtained as a coefficient in a linear regression. For each variant alone, there is unlikely to be enough information to make inference about association, unless the sample size is unfeasibly large. However, if the gene is not associated with the trait, then the distribution of estimates across all variants will be Gaussian with mean zero. Conversely, if variants in the gene are associated with the trait, there will be a mixture of Gaussian distributions with different means, manifested as “overdispersion”, which can be detected by a C-alpha test.
More formally, let denote the effect estimate, and it's corresponding estimate of standard deviation, at variant k, k = 1,…,K. We assume that are independent Gaussian distributed random variables with mean and standard deviation . As described, such estimates will typically have been obtained from a logistic (binary trait) or linear (quantitative trait) regression of trait value on genotype. The C-alpha test of homogeneity can be derived for a given sampling model. Here the effects are treated as sampling units from a Gaussian sampling model. Under the null hypothesis of no association with the trait, we assume that all are equal to some fixed, unknown value, denoted . Under the alternative hypothesis, we assume that the take on a mixture of values, centred at . The C-alpha test statistic for a test of homogeneity of against a central mixture of alternative Gaussian hypotheses is
where is an estimate of under the null hypothesis. In practice, we estimate by the observed standard deviation . Notice that S is simply the sum of the differences between the variance of the observed measures of association and the expected variance under the null hypothesis. To standardise S, we require the estimated normalizing variance The standardised C-alpha test statistic is then which is asymptotically standard Gaussian distributed. The null hypothesis of no association is rejected for values of ZNORM significantly larger than that expected using a one-tailed test of size α. The quantities S and c are easily derived using methods detailed in Zelterman and Chen [12] for sampling units from a distribution belonging to the exponential family: in this case, the Gaussian distribution, where is treated as a nuisance parameter. Note that a natural adjustment for the effect of non-genetic risk factors can be achieved by including covariates in the regression model used to estimate . Furthermore, we can consider imputed variation by replacing direct genotypes with dosages under an additive model, or by maximisation of the missing data likelihood of the distribution of genotypes.For genetic association studies, the expected effect of a minor allele is zero, so that , and the C-alpha statistic reduces to:
The assumption that the distribution of ZNORM is Gaussian depends on: (i) the degree of sparseness in the data, as summarised by the relationship between sample size and MAF at each variant; (ii) the number of variants that are considered and (iii) the independence of variants. When the data are too sparse, because the sample size is too small and/or the MAF too low, the maximum likelihood estimates of effect size computed at each site are typically unstable. Furthermore, the discrepancy between the empirical variance of the estimates, and their variance under the reference asymptotic distribution can be large, resulting in inaccurate type I error [21]. It is reasonable to assume that large numbers of individuals will be genotyped because in a practical study design, tests require large numbers of individuals for adequate power, however the minimum MAF must be constrained to ensure stability of estimates in the presence of, for example, private mutations. The second and third requirements ensure convergence of the null distribution of the ZNORM to Gaussian by the central limit theorem. To estimate significance accurately for low MAF, where small numbers of variants are considered or where variants are correlated, standard permutation testing is required. See Text S1 for details of the standard permutation approach utilised here.Simulation Study
We conduct simulations to investigate the performance of the Generalised C-alpha test for the identification of rare variants associated with a binary or quantitative trait. We compare the performance of the Generalised C-alpha test to three existing approaches: (i) the optimized score-based variance component test (SKAT-O, by Lee et al. [15] (ii) the Binomial C-alpha rare variant test by Neale et al. [14], and (iii) GRANVIL, a burden test of association of binary or quantitative traits with accumulations of minor alleles at rare variants in a generalised linear modelling framework by Morris and Zeggini [10]. A short summary of these tests is given here.
-
SKAT-O performs a test of association between genetic variants in a region and binary or continuous traits using kernel machine methods. SKAT-O aggregates individual score test statistics obtained at each variant to compute an overall p-value for the region. SKAT-O can be applied to imputed data and can allow adjustment for covariates.
-
The Binomial C-alpha test is a rare variant test developed for binary (disease) traits. The test models the number of minor alleles, yk, at variant k out of a total of nk observations by a binomial (nk, pk) distribution, where k = 1,…,K. Under the null hypothesis, pk = p0, the proportion of cases present in the sample. Under the alternative hypothesis, pk can take on a mixture of values across the K variants, with some variants deleterious (i.e. with greater frequency in the cases than controls, pk>p0), some protective (i.e. with greater frequency in the controls than the cases pk<p0), and some neutral (i.e. with equal frequency in cases and controls pk = p0). It can then be shown that the Binomial C-alpha test statistic is simply:
ZBIN has a standard Gaussian distribution under the null hypothesis of no association, which is rejected for values of ZBIN significantly larger than that expected for a one-tailed test of size α. The Binomial C-alpha test cannot adjust for covariates and cannot be directly applied to imputed data. -
GRANVIL models the trait value of an individual as a function of the proportion of rare variants at which they carry at least one minor allele in a generalised linear regression framework. GRANVIL can thus be applied to binary and quantitative traits, can incorporate imputed genotypes, and can allow adjustment for covariates. However, GRANVIL is a burden test, and thus assumes the direction of effect of all rare variants is the same, within the same gene or pathway.
Our simulations make use of a simple model of population genetics to generate high-density haplotype data in 30–200 kb genomic regions, designed to represent a gene. Haplotypes are then randomly paired together to form individuals for analysis, and quantitative trait values are generated according to their genotypes at rare causal variants, selected at random according to the underlying trait association model. In the trait association model that we consider here, we assume that the expected phenotypic value of an individual is determined by the net effect of a combination of increaser causal variants, which serve to elevate the mean trait value in the population, and decreaser causal variants, which serve to reduce it. The trait association model is parameterised in terms of: (i) the maximum MAF of each individual causal variant; (ii) the total MAF of all causal variants in the gene; (iii) the relative proportion of increaser and decreaser causal variants; and (iv) the joint contribution of the causal variants in the gene to the trait variance. Full details of the simulation process are described in Text S1.
The Generalised C-alpha test, SKAT-O and GRANVIL are applied directly to the simulated quantitative trait. However, to apply tests designed for binary traits, we dichotomise the quantitative distribution by assigning individuals as “cases” if they belong to the upper 50% of the trait distribution, or “controls” otherwise. The Generalised C-alpha test, as well as the Binomial C-alpha test, is then applied to the dichotomised trait. The significance of the Generalised C-alpha and Binomial C-alpha test statistics are evaluated empirically by standard permutation testing (see Text S1 for details), whilst GRANVIL relies on the asymptotic properties of a linear regression model and SKAT-O uses Davies method [22] for approximating the distribution of the test statistic. For each simulation, we permute 1,000 or 100,000 times to ensure accurate assessment at 0.05 and 1×10−5 significance levels, respectively. Simulations are repeated 10,000 times for each set of parameter values.
Rare Variant Analysis of Imputed Data with T1D
We evaluated the evidence for rare variant (MAF<1%) signals of association with T1D in genes on chromosome 6 using the Generalised C-alpha test applied to rare variants using genotype data from the WTCCC [18]. All WTCCC samples are ascertained from the UK. We applied the same quality control (QC) filters employed and described by the WTCCC to exclude samples and SNPs from the analysis. These high-quality samples were imputed up to the Phase 1 1000 Genomes Project reference panel (June 2011 interim release) [5] comprising 1,094 phased individuals from multiple ancestry groups. Adjustment for fine-scale population structure is critical in rare variant analysis because recent founder effects can exert greater impact on association analyses with rare variants than with common variants [23]. To control for population structure we constructed principal components to represent axes of genetic variation within the UK and included these as covariates in association analyses to obtain estimates of effect at each SNP that are adjusted for ancestry. These procedures for imputation and control of fine-scale population structure are the same as those utilised by Magi et al. [24], full details of which are presented in their paper.
For each gene, the Generalised C-alpha test was applied to SNPs in two MAF ranges: 0.1%<MAF<0.5% (very rare) and 0.5%<MAF<1% (rare). Measures of effect at each SNP used in the Generalised C-alpha test were the log odds ratios estimated from single SNP additive tests of association using simple logistic regression. The Generalised C-alpha test was applied to the original data and then, in order to determine a permuted p-value, to repeated permutations of the case/control status and covariate data (see Text S1 for details of the standard permutation approach). We performed two separate analyses with and without adjustment for the lead MHC SNP for T1D, rs9268645. Assuming there are approximately 30,000 genes in the human genome [25], a p-value of less than 0.05/30,000 = 1.7×10−6 is required to ensure genome-wide significance. Hence for each analysis, we performed 600,000 permutations and declared genome-wide significance for a given gene if less than 1 of 600,000 (<1.7×10−6) permutations resulted in a C-alpha test statistic larger than the original.
Results
Simulation Study
The assumption that the C-alpha statistic is normally distributed under the null hypothesis depends on the quantity and independence of the variants considered as well as the accuracy of the individual estimates at each variant, which in turn depends on the sample size and the MAF. By considering regions of a fixed size and varying the minimum MAF of alleles considered and the sample size, we were able to effectively vary the number of variants and the allele frequency distribution in order to explore type I error and power.
Type I error
We began by considering evaluation of the type 1 error rate of the Generalised C-alpha test by performing simulations of 2,000 samples in a 50 kb region under a null model where there are no causal variants. Table 1 presents estimated type I errors of the Generalised C-alpha test applied to a quantitative trait and a binary trait (where the binary trait is a dichotomised version of the quantitative trait). Over all simulations, the mean number of rare variants with at least 4 copies of the minor allele (0.2%<MAF<1%) was 34; and with at least 10 copies (0.5%<MAF<1%) was 15. Results indicate that the type I error of the Generalised C-alpha tests applied to both the quantitative and the binary trait is well calibrated.
Tab. 1. Null simulations. 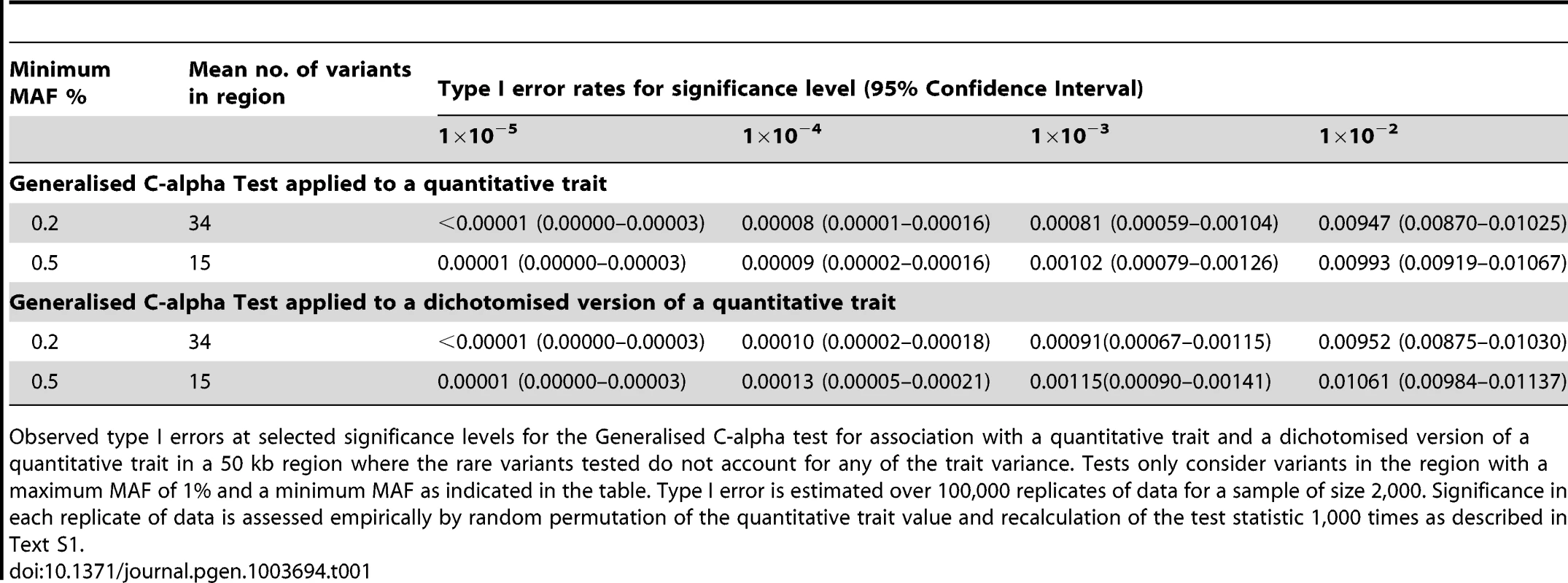
Observed type I errors at selected significance levels for the Generalised C-alpha test for association with a quantitative trait and a dichotomised version of a quantitative trait in a 50 kb region where the rare variants tested do not account for any of the trait variance. Tests only consider variants in the region with a maximum MAF of 1% and a minimum MAF as indicated in the table. Type I error is estimated over 100,000 replicates of data for a sample of size 2,000. Significance in each replicate of data is assessed empirically by random permutation of the quantitative trait value and recalculation of the test statistic 1,000 times as described in Text S1. Power comparison
Next, we considered evaluation of the power of the Generalised C-alpha test by performing simulations of 5,000 and 10,000 samples in a 100 kb region under a range of trait association models. In all simulations, we assume that the maximum MAF of any causal variant is 1%, and the total MAF of causal variants within the gene is 5%, which together account for 0.6% of the trait variance. Simulation results evaluating power are shown in Figure 1 for 10,000 samples and in Figure S1 for 5,000 samples. The Generalised C-Alpha tests, the Binomial C-alpha and SKAT-O are robust to the presence of a mixture of risk and protective variants.
Fig. 1. Power Comparisons. 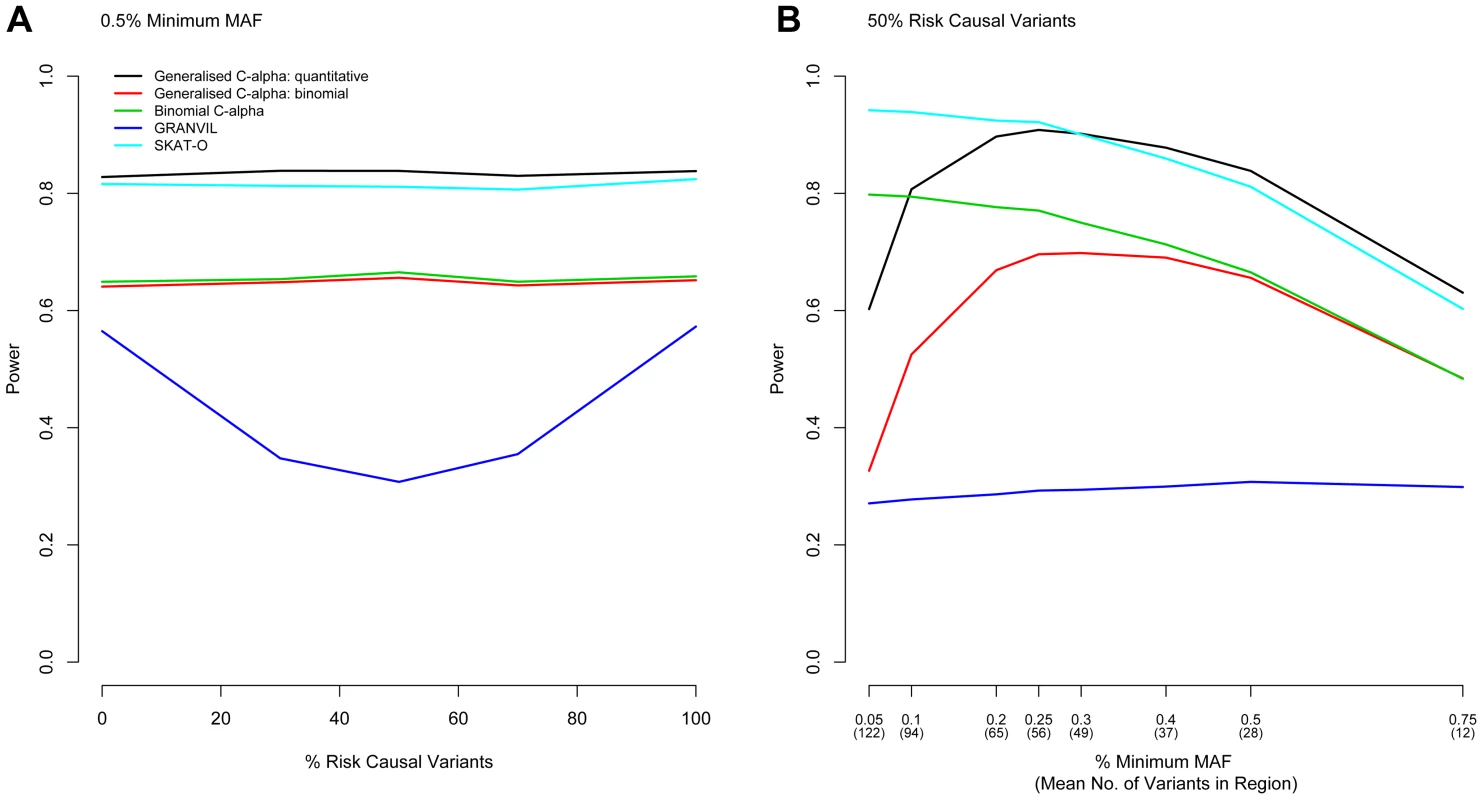
Power to detect association in a region is shown for the Generalised C-alpha test, SKAT-O and the GRANVIL test applied directly to the quantitative trait and for the Generalised C-alpha and the Binomial C-alpha tests applied to the dichotomised quantitative trait. (A) Power is shown as a function of the percentage of causal variants in a region of size 100 kb that are risk as opposed to protective when the minimum MAF of variants considered is fixed at 0.5% for a sample size of 10,000. Results show that as the proportion of risk causal variants approaches 50%, the C-alpha and SKAT-O tests maintain power and that the Generalised C-alpha applied directly to the quantitative trait has optimal power. (B) Power is also shown as a function of the minimum MAF of variants considered when the percentage of risk causal variants in a region of size 100 kb is fixed at 50% for a sample 10,000 individuals. Results show that the power of the Generalised C-alpha test is optimal for variants with MAF>∼0.3% but SKAT-O is optimal for lower MAF. For quantitative traits, the power of the Generalised C-alpha test remains better than the Binomial C-alpha applied to a dichotomized version of the trait as long as variants have MAF>∼0.1%. For binary traits, the Binomial C-alpha test has greater or equivalent power than the Generalised C-alpha test. For quantitative traits and sufficiently large minimum MAF (see asymptotic properties), the Generalised C-alpha performed better than all the other tests compared. In the examples we selected, it performed equally as well or better than SKAT-O for variants with more than ∼15–25 copies of the minor allele (MAF>∼0.3% for 5,000 samples or MAF>∼0.25% for 10,000 samples) for any combination of risk or protective variants (only shown for 50% risk causal variants). However, the SKAT-O was optimal for variants with fewer copies of the minor allele. In our qualitative analyses of a binary trait, the Binomial C-alpha test and the Generalised C-alpha test were comparable for variants with MAF>∼0.5% but the power of the Generalised C-alpha test declined for variants with fewer than ∼15–20 copies of the minor allele (MAF<∼0.3% for 5,000 samples and MAF<∼0.2% for 10,000 samples).
Asymptotic properties
The power of the Generalised C-alpha test applied to the quantitative and the dichotomised traits decreases rapidly as the number of copies of the minor allele for included rare variants falls below ∼10 in the models we have considered (MAF<∼0.2% for 5,000 samples or MAF<∼0.1% for 10,000 samples). Rapid decreases in power with decreasing MAF are likely to be a consequence of increasing sparseness leading to violation of the assumptions of asymptotic normality in the Generalised C-alpha test. Of course, in a given region, the total number of variants considered increases as the minimum MAF decreases – in simulations for 10,000 individuals, the number of variants in our simulated 100 kb region when minimum MAF is 0.5% is 28 increasing to 94 for a minimum MAF of 0.1% - and losses in power are also a consequence of an increased number of non-causal variants being included in this total, but this factor affects the power of all the tests similarly (Figure S2).
Computation time
Computation time for the Generalised C-alpha depends on the sample size, the number of markers and the method used to estimate the normally distributed measures of effect at each variant. To analyse all ∼160 markers sequenced on 5,000 or 10,000 individuals in a 100 kb region and obtain permuted p-values with 1,000 permutations in a Generalised C-alpha test of association required ∼5.0 s and ∼10 s, respectively, for a quantitative trait (using estimates of effect derived from linear regression) and ∼20% longer for a binary trait (using estimates of effect derived from logistic regression). Increasing the number of permutations to 100,000 increased the run times ∼20-fold. Halving the number of markers analysed only marginally reduced run times. These estimates were based on simple code programmed in R and run on a Unix operating system. Coding in a language that allows faster numerical computation times is expected to reduce run times.
Rare Variant Analysis of Imputed Data with T1D
After QC and imputation, the WTCCC data comprised 2,938 T1D cases and 1,963 controls with directly or imputed genotypes available at 490,888 SNPs with 0<MAF<1%, located in 1,611 distinct genes on chromosome 6; gene boundaries were identified from the UCSC human genome database (build 37). Table 2 shows the genes demonstrating genome-wide significant evidence of rare variant association with type-1 diabetes on chromosome 6. Genome-wide significant (Bonferroni correction for 30,000 genes at a 5% significance level: p<1.7×10−6) evidence of association with T1D were observed with rare variants in 17 genes throughout the 7.5 Mb extended Major Histocompatibility Complex (MHC) region (ranging from the GNL1 gene to the COL11A2 gene). The strongest signal of association was observed at C6orf10 (ZNORM = 89.1, p<1.7×10−6), which contains rare variants previously implicated in susceptibility to T1D [26].
Tab. 2. Genes demonstrating genome-wide significant evidence of rare variant association with type-1 diabetes on chromosome 6. 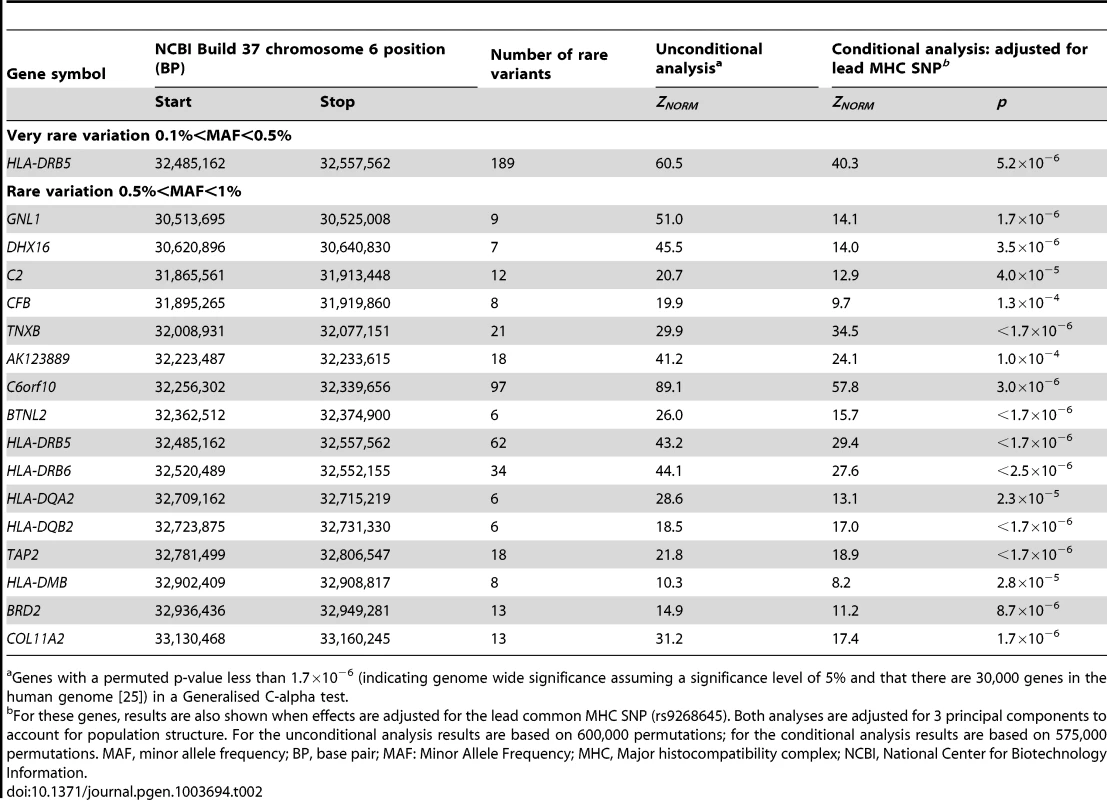
Genes with a permuted p-value less than 1.7×10−6 (indicating genome wide significance assuming a significance level of 5% and that there are 30,000 genes in the human genome [25]) in a Generalised C-alpha test. Common SNPs in the MHC have been previously associated with T1D [17], [20]. Exactly which and how many loci in the MHC determine susceptibility remains unclear as a consequence of the high gene density and the strong association between alleles in the region. To take account of established associations in the MHC, we repeated our analyses on the genes with rare variants showing genome-wide significance evidence of association with T1D with adjustment for the lead MHC SNP (rs9268645) [17]. The common SNP explained the rare variant association in 11 of the MHC genes; 6 MHC genes achieved genome-wide significant evidence of rare variant association with T1D after adjustment for the lead MHC SNP.
Discussion
We have developed the Generalised C-alpha test for the analysis of multiple rare variants that display a mixture of increaser and decreaser effects on a binary or quantitative trait. The Generalised C-alpha test is a score test combining routinely calculated Gaussian distributed measures of effect at multiple variants in order to increase the power to detect an effect at the gene, region or pathway level. The Binomial C-alpha test for binary traits, [14] and, more recently, SKAT-O [15], have been shown to have several advantages over previously proposed tests by Li and Leal [8], Madsen and Browning [9] and Price et al. [11]: most notably increased power in the presence of a mixture of increaser and decreaser effects. Our results confirm that the Generalised C-alpha test is also robust to the presence of bi-directional effects, with no apparent loss in power across a range of different mixtures.
The Generalised C-alpha test performs better than SKAT-O when the data is not too sparse: in our examples we showed the Generalised C-alpha was optimal as long as there were at least 15–25 copies of a minor allele at each rare variant. When data is sparse, so that either the sample size is too small and/or the MAF is too low, estimates of allelic effects at each SNP are not robust, and the asymptotic assumptions on which the Generalised C-alpha test are based are inappropriate. Similarly, for testing rare variant association with a binary trait, we have shown that the Generalised C-alpha test has lower power that the Binomial C-alpha test in the presence of variants with very low minor allele counts: a minimum MAF>∼0.5% is recommended in order to achieve comparable power in these tests.
In any application, the Generalised C-alpha test works on the assumptions that there are (i) a sufficiently large set of variants; (ii) that estimates of effect based on these variants are robust and independent and; (iii) normally distributed. These assumptions are often unrealistic: they are violated for example, in the presence of linkage disequilibrium, small sample size, low MAF or few variants. Hence, it is imperative that permutation testing is employed for accurate estimation of significance. For analysis of the whole genome, 1,000 permutations, for which a simply coded version of the test can be run in a matter of seconds, is recommended as a first approach; regions where the test is significant with a p-value<0.001 can then be rerun with 100,000 or more permutations for an accurate estimate of genome-wide significance.
Unlike the Binomial C-alpha test, the Generalised C-alpha test can naturally adjust for additional covariates and can easily incorporate imputed variation. Unlike SKAT-O, the Generalised C-alpha test can be applied to summary statistics, without requirement of the individual level genotype data. For example, the Generalised C-alpha test can be quickly and easily applied to published data. However, this is recommended only for discovery as permutation testing cannot be implemented in this case and test statistics are likely to be inflated leading to increased type I errors: In this case, any regions identified would require further investigation for any confirmation of association.
Evaluation of rare variants extracted from existing GWAS data via imputation up to re-sequencing reference panels, such as those made available by the 1000 Genomes Project, has been demonstrated to be feasible [18]. We applied the Generalised C-alpha test to rare variants imputed into the WTCCC T1D GWAS across the MHC where genes have been shown to play the single most important role in susceptibility to T1D in both common variant and haplotype analyses. Genome-wide significant association with T1D, independent of the lead common variant GWAS signal in the region, was observed at multiple genes. These included HLA class II genes, DR and DQ, where coding polymorphisms have been shown to account for most of the association with T1D observed at the HLA locus [27], [28], [29]. The identification of rare disease-associated variants within genes in this region highlights the complex genetic architecture of T1D in the MHC, and requires further investigation to disentangle the effects of common and rare variation on immune disease susceptibility.
In summary, the Generalised C-alpha test is a novel, flexible and powerful method for the analysis of rare genetic variation. There is no single alternative test, amongst those we have considered, that is uniformly most powerful over all models and genetic architectures. Our test, however, has the unique advantage that it can be applied to summary statistics from published literature, without the need for individual level genetic data. The fact that the Generalised C-alpha test simply aggregates data from summary statistics allows for great flexibility in general allowing direct application to both binary and quantitative traits, to population (using summary statistics from generalized linear models, as illustrated here) and family based data (using summary statistics from the transmission disequilibrium test, for example), and to imputed genotype data whilst simultaneously allowing for the adjustment of additional covariates. We are already using the method in our analyses and it is currently implemented using the R-PLINK/SEQ library available from: http://atgu.mgh.harvard.edu/plinkseq/. R package is available from http://www.well.ox.ac.uk/~rivas/calphanorm.tar.gz.
Supporting Information
Zdroje
1. GudbjartssonDF, WaltersGB, ThorleifssonG, StefanssonH, HalldorssonBV, et al. (2008) Many sequence variants affecting diversity of adult human height. Nat Genet 40 : 609–615.
2. LettreG, JacksonAU, GiegerC, SchumacherFR, BerndtSI, et al. (2008) Identification of ten loci associated with height highlights new biological pathways in human growth. Nat Genet 40 : 584–591.
3. WeedonMN, LangoH, LindgrenCM, WallaceC, EvansDM, et al. (2008) Genome-wide association analysis identifies 20 loci that influence adult height. Nature genetics 40 : 575–583.
4. Lango AllenH, EstradaK, LettreG, BerndtSI, WeedonMN, et al. (2010) Hundreds of variants clustered in genomic loci and biological pathways affect human height. Nature 467 : 832–838.
5. A map of human genome variation from population-scale sequencing. Nature 467 : 1061–1073.
6. CohenJC, KissRS, PertsemlidisA, MarcelYL, McPhersonR, et al. (2004) Multiple rare alleles contribute to low plasma levels of HDL cholesterol. Science 305 : 869–872.
7. MorgenthalerS, ThillyWG (2007) A strategy to discover genes that carry multi-allelic or mono-allelic risk for common diseases: a cohort allelic sums test (CAST). Mutation research 615 : 28–56.
8. LiB, LealSM (2008) Methods for detecting associations with rare variants for common diseases: application to analysis of sequence data. American journal of human genetics 83 : 311–321.
9. MadsenBE, BrowningSR (2009) A groupwise association test for rare mutations using a weighted sum statistic. PLoS genetics 5: e1000384.
10. MorrisAP, ZegginiE (2010) An evaluation of statistical approaches to rare variant analysis in genetic association studies. Genet Epidemiol 34 : 188–193.
11. PriceAL, KryukovGV, de BakkerPI, PurcellSM, StaplesJ, et al. (2010) Pooled association tests for rare variants in exon-resequencing studies. American journal of human genetics 86 : 832–838.
12. ZeltermanD, ChenCF (1988) Homogeneity Tests against Central-Mixture Alternatives. Journal of the American Statistical Association 83 : 179–182.
13. NeymanJ, ScottE (1966) On the use of c(α) optimal tests of composite hypotheses. Bulletin of the International Statistical Institute 41 : 477–497.
14. NealeBM, RivasMA (2011) Testing for an unusual distribution of rare variants. PLoS Genet 7.
15. WuMC, LeeS, CaiT, LiY, BoehnkeM, et al. (2011) Rare-variant association testing for sequencing data with the sequence kernel association test. American journal of human genetics 89 : 82–93.
16. LeeS, WuMC, LinX (2012) Optimal tests for rare variant effects in sequencing association studies. Biostatistics 13 : 762–775.
17. BarrettJC, ClaytonDG, ConcannonP, AkolkarB, CooperJD, et al. (2009) Genome-wide association study and meta-analysis find that over 40 loci affect risk of type 1 diabetes. Nature genetics 41 : 703–707.
18. HuangJ, EllinghausD, FrankeA, HowieB, LiY (2012) 1000 Genomes-based imputation identifies novel and refined associations for the Wellcome Trust Case Control Consortium phase 1 Data. European Journal of Human Genetics 2012;20 : 801–805 doi: 10.1038/ejhg.2012.3
19. LiY, ByrnesAE, LiM (2010) To identify associations with rare variants, just WHaIT: Weighted haplotype and imputation-based tests. American journal of human genetics 87 : 728–735.
20. Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature 447 : 661–678.
21. CochranWG (1952) The Chi-2 Test of Goodness of Fit. Annals of Mathematical Statistics 23 : 315–345.
22. DaviesR (1980) The distribution of a linear combination of chi-square random variables. J R Stat Soc Ser C Appl Stat 29 : 323–333.
23. BodmerW, BonillaC (2008) Common and rare variants in multifactorial susceptibility to common diseases. Nature genetics 40 : 695–701.
24. MagiR, AsimitJL, Day-WilliamsAG, ZegginiE, MorrisAP (2012) Genome-Wide Association Analysis of Imputed Rare Variants: Application to Seven Common Complex Diseases. Genet Epidemiol 2012 Sep 5. doi: 10.1002/gepi.21675
25. Finishing the euchromatic sequence of the human genome. Nature 431 : 931–945.
26. FengT, ZhuX (2010) Genome-wide searching of rare genetic variants in WTCCC data. Human genetics 128 : 269–280.
27. NobleJA, ValdesAM, CookM, KlitzW, ThomsonG, et al. (1996) The role of HLA class II genes in insulin-dependent diabetes mellitus: molecular analysis of 180 Caucasian, multiplex families. American journal of human genetics 59 : 1134–1148.
28. SheJX (1996) Susceptibility to type I diabetes: HLA-DQ and DR revisited. Immunology today 17 : 323–329.
29. ToddJA (1995) Genetic analysis of type 1 diabetes using whole genome approaches. Proceedings of the National Academy of Sciences of the United States of America 92 : 8560–8565.
Štítky
Genetika Reprodukční medicína
Článek Re-Ranking Sequencing Variants in the Post-GWAS Era for Accurate Causal Variant IdentificationČlánek Bypass of 8-oxodGČlánek Integrated Model of and Inherited Genetic Variants Yields Greater Power to Identify Risk GenesČlánek Comparative Genomic and Functional Analysis of 100 Strains and Their Comparison with Strain GGČlánek A Nuclear Calcium-Sensing Pathway Is Critical for Gene Regulation and Salt Stress Tolerance inČlánek Computational Identification of Diverse Mechanisms Underlying Transcription Factor-DNA OccupancyČlánek Reversible and Rapid Transfer-RNA Deactivation as a Mechanism of Translational Repression in StressČlánek Genome-Wide Association of Body Fat Distribution in African Ancestry Populations Suggests New Loci
Článek vyšel v časopisePLOS Genetics
Nejčtenější tento týden
2013 Číslo 8- Srdeční frekvence embrya může být faktorem užitečným v předpovídání výsledku IVF
- Transthyretinová amyloidóza z pohledu neurologa a kardiologa aneb jak se vyhnout „misdiagnostice“?
- Akutní intermitentní porfyrie
- Pánevní endometrióza spojená s volnou tekutinou v peritoneální dutině snižuje úspěšnost otěhotnění po intrauterinní inseminaci
- Jak zlepšit účinnost psychofarmakoterapie a adherenci k ní pomocí farmakogenetiky? – kazuistiky z české praxe
-
Všechny články tohoto čísla
- Genome-Wide DNA Methylation Analysis of Systemic Lupus Erythematosus Reveals Persistent Hypomethylation of Interferon Genes and Compositional Changes to CD4+ T-cell Populations
- Re-Ranking Sequencing Variants in the Post-GWAS Era for Accurate Causal Variant Identification
- Histone Variant HTZ1 Shows Extensive Epistasis with, but Does Not Increase Robustness to, New Mutations
- Past Visits Present: TCF/LEFs Partner with ATFs for β-Catenin–Independent Activity
- Functional Characterisation of Alpha-Galactosidase A Mutations as a Basis for a New Classification System in Fabry Disease
- A Flexible Approach for the Analysis of Rare Variants Allowing for a Mixture of Effects on Binary or Quantitative Traits
- Masculinization of Gene Expression Is Associated with Exaggeration of Male Sexual Dimorphism
- Genic Intolerance to Functional Variation and the Interpretation of Personal Genomes
- Endogenous Stress Caused by Faulty Oxidation Reactions Fosters Evolution of 2,4-Dinitrotoluene-Degrading Bacteria
- Transposon Domestication versus Mutualism in Ciliate Genome Rearrangements
- Comparative Anatomy of Chromosomal Domains with Imprinted and Non-Imprinted Allele-Specific DNA Methylation
- An Essential Function for the ATR-Activation-Domain (AAD) of TopBP1 in Mouse Development and Cellular Senescence
- Depletion of Retinoic Acid Receptors Initiates a Novel Positive Feedback Mechanism that Promotes Teratogenic Increases in Retinoic Acid
- Bypass of 8-oxodG
- Calpain-6 Deficiency Promotes Skeletal Muscle Development and Regeneration
- ATM Release at Resected Double-Strand Breaks Provides Heterochromatin Reconstitution to Facilitate Homologous Recombination
- Generation of Tandem Direct Duplications by Reversed-Ends Transposition of Maize Elements
- Loss of a Conserved tRNA Anticodon Modification Perturbs Cellular Signaling
- Integrated Model of and Inherited Genetic Variants Yields Greater Power to Identify Risk Genes
- High-Throughput Genetic and Gene Expression Analysis of the RNAPII-CTD Reveals Unexpected Connections to SRB10/CDK8
- Dynamic Rewiring of the Retinal Determination Network Switches Its Function from Selector to Differentiation
- β-Catenin-Independent Activation of TCF1/LEF1 in Human Hematopoietic Tumor Cells through Interaction with ATF2 Transcription Factors
- Genetic Mapping of Specific Interactions between Mosquitoes and Dengue Viruses
- A Highly Redundant Gene Network Controls Assembly of the Outer Spore Wall in
- Origin and Functional Diversification of an Amphibian Defense Peptide Arsenal
- Myc-Driven Overgrowth Requires Unfolded Protein Response-Mediated Induction of Autophagy and Antioxidant Responses in
- Integrative Modeling of eQTLs and Cis-Regulatory Elements Suggests Mechanisms Underlying Cell Type Specificity of eQTLs
- Species and Population Level Molecular Profiling Reveals Cryptic Recombination and Emergent Asymmetry in the Dimorphic Mating Locus of
- Ras-Induced Changes in H3K27me3 Occur after Those in Transcriptional Activity
- Characterization of the p53 Cistrome – DNA Binding Cooperativity Dissects p53's Tumor Suppressor Functions
- Global Analysis of Fission Yeast Mating Genes Reveals New Autophagy Factors
- Deficiency Suppresses Intestinal Tumorigenesis
- Introns Regulate Gene Expression in in a Pab2p Dependent Pathway
- Meiotic Recombination Initiation in and around Retrotransposable Elements in
- Comparative Oncogenomic Analysis of Copy Number Alterations in Human and Zebrafish Tumors Enables Cancer Driver Discovery
- Comparative Genomic and Functional Analysis of 100 Strains and Their Comparison with Strain GG
- A Model-Based Analysis of GC-Biased Gene Conversion in the Human and Chimpanzee Genomes
- Masculinization of the X Chromosome in the Pea Aphid
- The Architecture of a Prototypical Bacterial Signaling Circuit Enables a Single Point Mutation to Confer Novel Network Properties
- Distinct SUMO Ligases Cooperate with Esc2 and Slx5 to Suppress Duplication-Mediated Genome Rearrangements
- The Yeast Environmental Stress Response Regulates Mutagenesis Induced by Proteotoxic Stress
- Mediator Directs Co-transcriptional Heterochromatin Assembly by RNA Interference-Dependent and -Independent Pathways
- The Genome of and the Basis of Host-Microsporidian Interactions
- Regulation of Sister Chromosome Cohesion by the Replication Fork Tracking Protein SeqA
- Neuronal Reprograming of Protein Homeostasis by Calcium-Dependent Regulation of the Heat Shock Response
- A Nuclear Calcium-Sensing Pathway Is Critical for Gene Regulation and Salt Stress Tolerance in
- Cross-Species Array Comparative Genomic Hybridization Identifies Novel Oncogenic Events in Zebrafish and Human Embryonal Rhabdomyosarcoma
- : A Mouse Strain with an Ift140 Mutation That Results in a Skeletal Ciliopathy Modelling Jeune Syndrome
- The Relative Contribution of Proximal 5′ Flanking Sequence and Microsatellite Variation on Brain Vasopressin 1a Receptor () Gene Expression and Behavior
- Combining Quantitative Genetic Footprinting and Trait Enrichment Analysis to Identify Fitness Determinants of a Bacterial Pathogen
- The Innocence Project at Twenty: An Interview with Barry Scheck
- Computational Identification of Diverse Mechanisms Underlying Transcription Factor-DNA Occupancy
- GUESS-ing Polygenic Associations with Multiple Phenotypes Using a GPU-Based Evolutionary Stochastic Search Algorithm
- H2A.Z Acidic Patch Couples Chromatin Dynamics to Regulation of Gene Expression Programs during ESC Differentiation
- Identification of DSB-1, a Protein Required for Initiation of Meiotic Recombination in , Illuminates a Crossover Assurance Checkpoint
- Binding of TFIIIC to SINE Elements Controls the Relocation of Activity-Dependent Neuronal Genes to Transcription Factories
- Global Analysis of the Sporulation Pathway of
- Genetic Circuits that Govern Bisexual and Unisexual Reproduction in
- Deletion of microRNA-80 Activates Dietary Restriction to Extend Healthspan and Lifespan
- Fifty Years On: GWAS Confirms the Role of a Rare Variant in Lung Disease
- The Enhancer Landscape during Early Neocortical Development Reveals Patterns of Dense Regulation and Co-option
- Gene Expression Regulation by Upstream Open Reading Frames and Human Disease
- Sociogenomics of Cooperation and Conflict during Colony Founding in the Fire Ant
- The Intronic Long Noncoding RNA Recruits PRC2 to the Promoter, Reducing the Expression of and Increasing Cell Proliferation
- The , p.E318G Variant Increases the Risk of Alzheimer's Disease in -ε4 Carriers
- The Wilms Tumor Gene, , Is Critical for Mouse Spermatogenesis via Regulation of Sertoli Cell Polarity and Is Associated with Non-Obstructive Azoospermia in Humans
- Reversible and Rapid Transfer-RNA Deactivation as a Mechanism of Translational Repression in Stress
- QTL Analysis of High Thermotolerance with Superior and Downgraded Parental Yeast Strains Reveals New Minor QTLs and Converges on Novel Causative Alleles Involved in RNA Processing
- Genome Wide Association Identifies Novel Loci Involved in Fungal Communication
- Chromatin Sampling—An Emerging Perspective on Targeting Polycomb Repressor Proteins
- A Recessive Founder Mutation in Regulator of Telomere Elongation Helicase 1, , Underlies Severe Immunodeficiency and Features of Hoyeraal Hreidarsson Syndrome
- Genome-Wide Association of Body Fat Distribution in African Ancestry Populations Suggests New Loci
- Causal and Synthetic Associations of Variants in the Gene Cluster with Alpha1-antitrypsin Serum Levels
- Hard Selective Sweep and Ectopic Gene Conversion in a Gene Cluster Affording Environmental Adaptation
- Brittle Culm1, a COBRA-Like Protein, Functions in Cellulose Assembly through Binding Cellulose Microfibrils
- Chromosomal Copy Number Variation, Selection and Uneven Rates of Recombination Reveal Cryptic Genome Diversity Linked to Pathogenicity
- The Ribosomal Protein Rpl22 Controls Ribosome Composition by Directly Repressing Expression of Its Own Paralog, Rpl22l1
- Ras1 Acts through Duplicated Cdc42 and Rac Proteins to Regulate Morphogenesis and Pathogenesis in the Human Fungal Pathogen
- The DSB-2 Protein Reveals a Regulatory Network that Controls Competence for Meiotic DSB Formation and Promotes Crossover Assurance
- Recurrent Modification of a Conserved -Regulatory Element Underlies Fruit Fly Pigmentation Diversity
- Associations of Mitochondrial Haplogroups B4 and E with Biliary Atresia and Differential Susceptibility to Hydrophobic Bile Acid
- The Conditional Nature of Genetic Interactions: The Consequences of Wild-Type Backgrounds on Mutational Interactions in a Genome-Wide Modifier Screen
- A Critical Function of Mad2l2 in Primordial Germ Cell Development of Mice
- A Role for CF1A 3′ End Processing Complex in Promoter-Associated Transcription
- Vitellogenin Underwent Subfunctionalization to Acquire Caste and Behavioral Specific Expression in the Harvester Ant
- PLOS Genetics
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Chromosomal Copy Number Variation, Selection and Uneven Rates of Recombination Reveal Cryptic Genome Diversity Linked to Pathogenicity
- Genome-Wide DNA Methylation Analysis of Systemic Lupus Erythematosus Reveals Persistent Hypomethylation of Interferon Genes and Compositional Changes to CD4+ T-cell Populations
- Associations of Mitochondrial Haplogroups B4 and E with Biliary Atresia and Differential Susceptibility to Hydrophobic Bile Acid
- A Role for CF1A 3′ End Processing Complex in Promoter-Associated Transcription
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání







