-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaUbiquitous Polygenicity of Human Complex Traits: Genome-Wide Analysis of 49 Traits in Koreans
Recent studies in population of European ancestry have shown that 30%∼50% of heritability for human complex traits such as height and body mass index, and common diseases such as schizophrenia and rheumatoid arthritis, can be captured by common SNPs and that genetic variation attributed to chromosomes are in proportion to their length. Using genome-wide estimation and partitioning approaches, we analysed 49 human quantitative traits, many of which are relevant to human diseases, in 7,170 unrelated Korean individuals genotyped on 326,262 SNPs. For 43 of the 49 traits, we estimated a nominally significant (P<0.05) proportion of variance explained by all SNPs on the Affymetrix 5.0 genotyping array (). On average across 47 of the 49 traits for which the estimate of is non-zero, common SNPs explain approximately one-third (range of 7.8% to 76.8%) of narrow sense heritability.
The estimate of is highly correlated with the proportion of SNPs with association P<0.031 (r2 = 0.92). Longer genomic segments tend to explain more phenotypic variation, with a correlation of 0.78 between the estimate of variance explained by individual chromosomes and their physical length, and 1% of the genome explains approximately 1% of the genetic variance. Despite the fact that there are a few SNPs with large effects for some traits, these results suggest that polygenicity is ubiquitous for most human complex traits and that a substantial proportion of the “missing heritability” is captured by common SNPs.
Published in the journal: . PLoS Genet 9(3): e32767. doi:10.1371/journal.pgen.1003355
Category: Research Article
doi: https://doi.org/10.1371/journal.pgen.1003355Summary
Recent studies in population of European ancestry have shown that 30%∼50% of heritability for human complex traits such as height and body mass index, and common diseases such as schizophrenia and rheumatoid arthritis, can be captured by common SNPs and that genetic variation attributed to chromosomes are in proportion to their length. Using genome-wide estimation and partitioning approaches, we analysed 49 human quantitative traits, many of which are relevant to human diseases, in 7,170 unrelated Korean individuals genotyped on 326,262 SNPs. For 43 of the 49 traits, we estimated a nominally significant (P<0.05) proportion of variance explained by all SNPs on the Affymetrix 5.0 genotyping array (). On average across 47 of the 49 traits for which the estimate of is non-zero, common SNPs explain approximately one-third (range of 7.8% to 76.8%) of narrow sense heritability.
The estimate of is highly correlated with the proportion of SNPs with association P<0.031 (r2 = 0.92). Longer genomic segments tend to explain more phenotypic variation, with a correlation of 0.78 between the estimate of variance explained by individual chromosomes and their physical length, and 1% of the genome explains approximately 1% of the genetic variance. Despite the fact that there are a few SNPs with large effects for some traits, these results suggest that polygenicity is ubiquitous for most human complex traits and that a substantial proportion of the “missing heritability” is captured by common SNPs.Introduction
The five years wave of genome-wide association studies (GWAS) has uncovered thousands of single nucleotide polymorphisms (SNPs) to be associated with hundreds of human complex traits including common diseases [1], [2]. Yet, for most complex traits, the gap between the proportion of phenotypic variance accounted for by the top SNPs that reached genome-wide significance level in GWAS and the heritability estimated from pedigree analyses remains unexplained [3]. This was called the “missing heritability” problem [4], explanations to which have been debated in the field [3]. Taking height and BMI for example, well-powered studies with a discovery sample of over 100,000 individuals have identified 180 and 32 loci to be associated with height [5] and BMI [6], which explain ∼10% and ∼1.5% of variance for height and BMI, respectively, while the heritability was estimated to be ∼80% for height [7] and 40∼60% for BMI [8], [9]. On the other hand, however, recent studies using whole-genome estimation approaches have demonstrated that a large proportion of heritability for height [10], [11], body mass index (BMI) [11], schizophrenia [12] and rheumatoid arthritis (RA) [13] can be captured by all the common SNPs on the current genotyping arrays, which implies that there are a large number of variants each with an effect too small to pass the stringent genome-wide significance level. It could be argued that the evidence from these whole-genome estimation analyses are for the traits that are known to be highly polygenic and therefore are not representative for most human complex traits. Therefore, it remains unclear whether polygenic inheritance is a general phenomenon for most human complex traits or a unique feature for a particular group of traits such as height and BMI. There has been evidence from a review of a number of GWAS that more variants have been identified with increased sample size [2], consistent with a pattern of polygenic inheritance for most common diseases and complex traits. In this study, using the whole-genome estimation and partitioning approaches [10], [11], [14], we directly estimated the proportion of phenotypic variance explained by the common SNPs all together on a genotyping array for a range of quantitative traits in a large homogenous sample of Koreans. We demonstrated by a number of different analyses that polygenic inheritance is likely to be ubiquitous for most human complex traits.
Results
We used the data from the Korea Association Resource (KARE) project [15]. The KARE cohort consists of 10,038 individuals recruited from two different sites in South Korea, genotyped at 500,568 SNPs on Affymetrix Human SNP array 5.0. There were 7,170 unrelated individuals and 326,262 autosomal SNPs after quality controls (Materials & Methods). We show by principal component analysis that all the individuals are of eastern Asian ancestry (Figure S1). All the individuals were measured for 49 quantitative traits, which are related to obesity, blood pressure, hyperglycemia, diabetes, liver functions, lung functions, and kidney functions (Table S1). The phenotypic correlations between pairwise traits are visualized in Figure S2, with traits within the same classification groups being more correlated than between groups.
We then estimated the proportion of variance explained by fitting all the SNPs in a mixed linear model for each of the 49 traits (Materials & Methods). In general, there was a substantial amount of variance explained by all SNPs on the Affymetrix 5.0 genotyping array () for most traits with a mean of 12.8% (a range from 0 to 31.6%) across all the 49 traits (Table 1). For 47 of the 49 traits, the estimate of was non-zero, 43 of which reached the nominal significance level (likelihood ratio test P<0.05) and 26 of which reached experimental-wise significance level after Bonferroni correction for multiple traits (likelihood ratio test P<0.001) [14]. We compared the estimates of with the narrow-sense heritability (h2) estimated from pedigree analyses in the literature (Table S2), and observed a significant trend (P = 0.017) that traits with a higher estimate of h2 were more likely to have a larger estimate of (Figure S3) and that all the common SNPs explain approximately 33.3% (a range from 7.8% to 76.8%) of the narrow-sense heritability, despite that the estimates of h2 were from various different studies, usually with large standard errors and mostly in samples of European ancestry. In contrast, when we performed a genome-wide association (GWA) analysis in the same sample, we identified genome-wide significant (P<5×10−8) SNPs for 25 of the 49 traits. On average across the 25 traits, the top associated SNPs from GWA analyses explained only 1.5% (range of 0.5% to 3.8%) of phenotypic variance (Table S2), nearly 10-fold smaller than the estimate of , suggesting there are many SNPs remaining undetected because of the lack of statistical power. In addition, we estimated the variance explained by all the SNPs imputed to HapMap2 CHB and JPT panels (Materials & Methods and Table S2). The estimate of averaged across all the traits using imputed data (13.8%) was slightly higher than that using genotyped data (12.8%).
Tab. 1. Estimates of variance explained by all SNPs for the 49 traits. 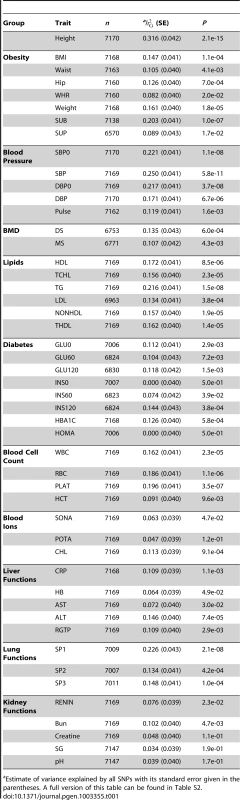
Estimate of variance explained by all SNPs with its standard error given in the parentheses. A full version of this table can be found in Table S2. We calculated the proportion of SNPs with p-values that passed a threshold p-value in a GWA analysis (θP) for each trait. We calculated θP for a range of threshold p-values and plotted them against the expected values under the null hypothesis of no association (i.e. the threshold p-values) (Figure S4). This plot is an analogue to the QQ plot. The averaged θP over all the traits started deviating from the expected value when the threshold p-value became small (Figure S4A) and such deviation varied across traits (Figure S4B). The question is whether a trait that shows a larger value of θP will also tend to have a larger estimate of . We then correlated θP with the estimates of across all the traits for a threshold p-value and calculated such correlations for a range of threshold p-values, from 0.001 to 0.201 by 0.05. We found a maximum of squared correlation of 0.923 at the threshold p-value of 0.031 (Figure 1), meaning that traits that have more proportion of SNPs passed a significance level in GWAS also have more proportion of phenotypic variance explained by all SNPs. It should be noted that the threshold p-value at which the maximum correlation between the estimate of and θP was found depends on sample size. This analysis is an alternative way to demonstrate the equivalence between GWAS and the whole-genome estimation analysis as implemented in GCTA. Although the whole-genome estimation approach estimates the variance explained by all SNPs regardless of individual SNP-trait associations, the estimate of is actually mainly attributed to SNPs that show stronger evidence for association with the trait, e.g. ∼92% of the estimate of could be determined by SNPs with association p-values<0.031 given the sample size of ∼7,000 in this study. These results also suggest that there are many common variants associated with the traits at nominally significant level (P<0.05) but their effect sizes are too small to be genome-wide significant (P<5×10−8).
Fig. 1. 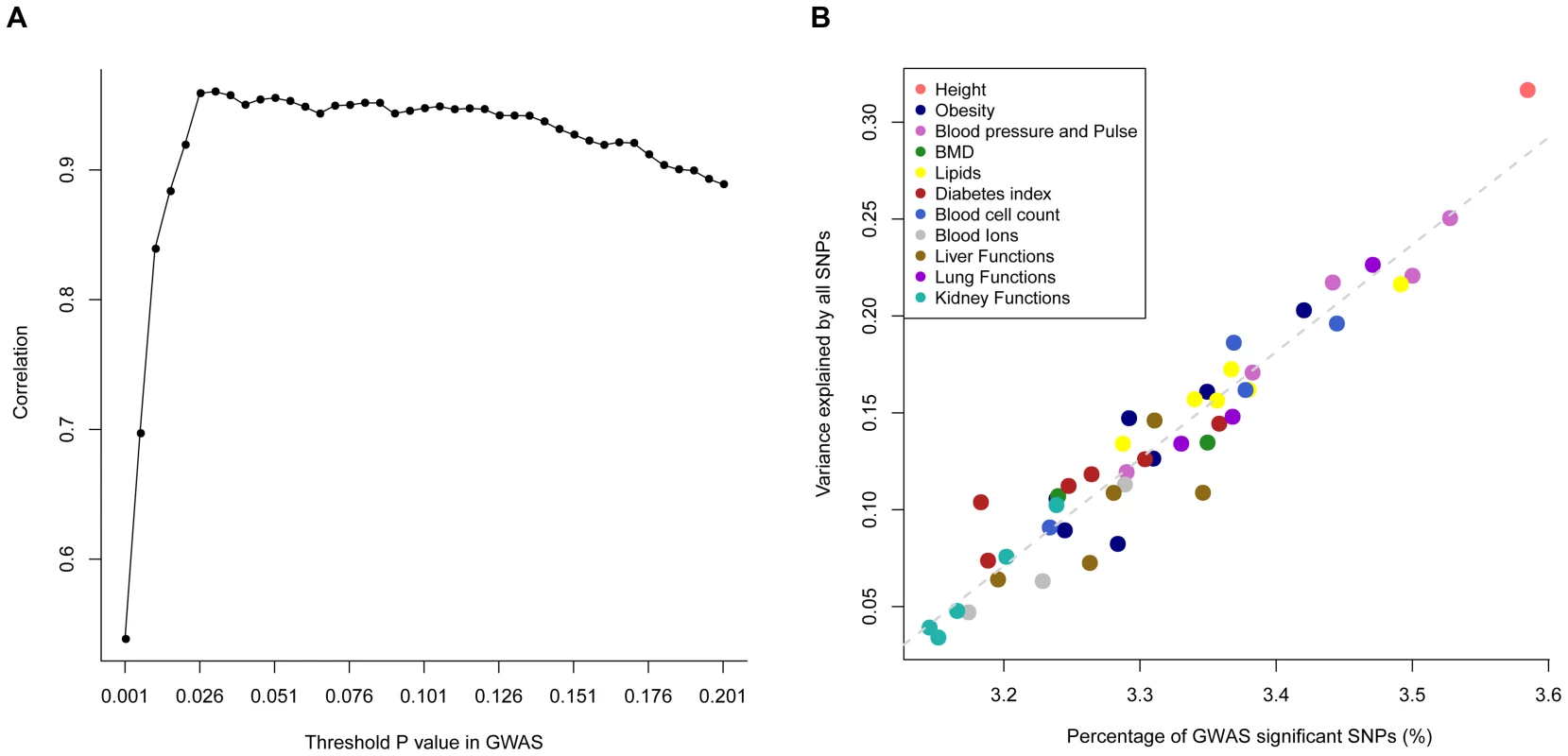
The proportion of GWAS significant SNPs (<i>θ</i><sub>P</sub>) is defined as the proportion of SNPs that passed a threshold <i>P</i> value (e.g. 0.01) in GWAS. Panel <b>A</b>): correlations (<i>r</i>) between <i>θ</i><sub>P</sub> and across 47 traits (all traits except INS0 and HOMA) for a range of threshold p-values. The maximum <i>r</i> value (<i>r</i><sub>max</sub> = 0.960) is at a threshold p-value of 0.031. Panel <b>B</b>): estimates of against <i>θ</i><sub>P</sub> at p-value of 0.031 for the 47 traits. Using the same method as above but allowing to fit multiple genetic components simultaneously in the model (Materials & Methods), we then partitioned into the contributions of individual chromosomes for all the 49 traits (Table S3) except HOMA and INS0 for which the estimates of were zero (Table 1), and plotted the estimate of variance explained by each chromosome () against chromosome length (LC) for each trait. We did not observe a linear correlation between and LC for any particular traits (Figure S5) as strong as that shown in the previous studies for height [11] and schizophrenia [12]. The squared correlation between and LC was from 0.00 to 0.48 with a mean of 0.15 and a standard deviation of 0.12. This result is not unexpected because the sample size of this study is smaller than that of the previous analysis so that in our analysis were estimated with larger sampling errors. We then averaged the estimates of over all the traits to reduce the sampling error variance and found that the averaged estimate of was strongly correlated with LC with a correlation of 0.78 (Figure 2A). We show by hierarchical cluster analysis that the correlation between averaged and LC was not driven by a few traits (Figure 3) and by randomly sampling the same number of SNPs from each chromosome that it was also not due to longer chromosomes having more SNPs (Figure S6). We also demonstrate that the estimates of on longer chromosomes were more variable than those on shorter chromosomes (Figure S7). We further took the weighted average of the estimates of across traits by , which is defined as the proportion of genetic variance attributed to each chromosome, and plotted it against the proportion of the genome represented by each chromosome (LC/L, with L being the total length of the genome) (Figure 2B). The regression slope of the proportion of the genetic variance attributed to each chromosome on the proportion of the genome represented by each chromosome was 0.875 with a standard error (SE) of 0.150 which was not significantly different from 1 (P = 0.413), and the intercept was 0.008 (SE = 0.007) which was not significantly different from zero (P = 0.289), suggesting that on average 1% of the genome approximately explains 1% of the genetic variance. Despite that there are SNPs with large effects for some traits (Figure S8), all these results are consistent with that many genetic variants each with a small effect widely spread across the whole genome.
Fig. 2. Proportion of variance attributed to each chromosome averaged across 47 traits against chromosome length. 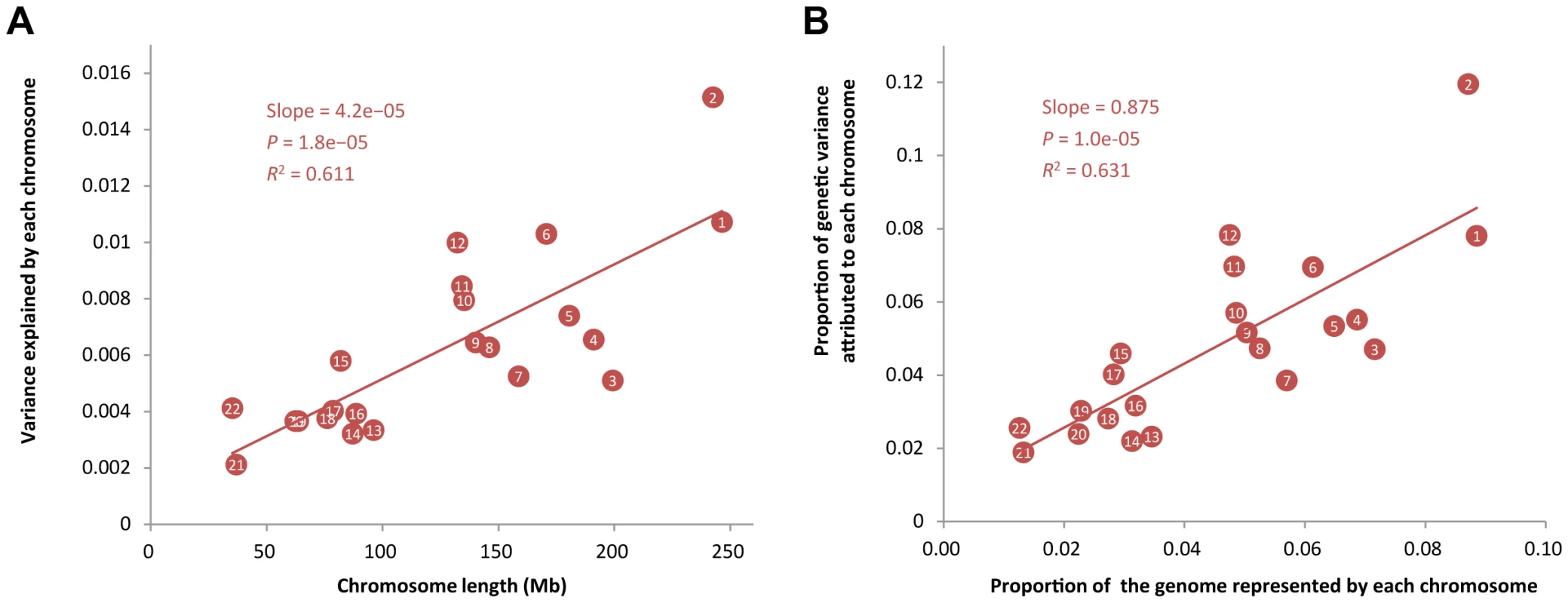
In panel A), shown on the y-axis is the averaged estimate of variance explained by each chromosome () across all the traits, except INS0 and HOMA, for which the estimates of variance explained by all SNPs () are zero. In panel B), the estimate of is weighted by for each trait, i.e. , and the length of each chromosome is divided by the total length of the genome, where the intercept (0.008, SE = 0.007) is not significantly different from zero (P = 0.289) and the slope (0.875, SE = 0.150) is not significantly different from 1, which is not significantly different from 1 (P = 0.413). Fig. 3. Heatmap of the proportions of variance explained attributed to individual chromosomes for 47 traits. 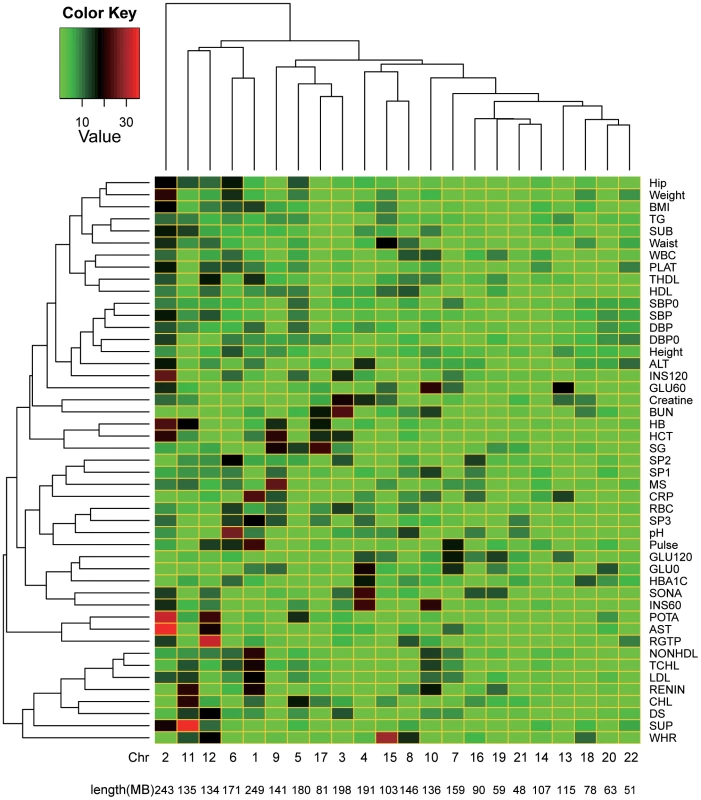
On the y-axis is the variance explained by each chromosome () weighted by the total variance explained by all SNPs () and averaged across all traits, except INS0 and HOMA, for which the estimates of are zero. The estimates of and the traits were clustered by the hierarchical clustering approach and the heatmap plot was generated by the gplots package in R. In addition, we partitioned into the contributions of genic () and intergenic () regions of the whole genome (Materials & Methods) and averaged the estimates of and across all the traits. The result shows that SNPs in genic regions explain disproportionally more variation than those in intergenic regions (Table S4). We further estimated the variance explained by the genic () and intergenic () regions of each chromosome and again averaged the estimates of and across all traits. The numbers of genic and intergenic SNPs on each chromosome are presented in Table S5. We show that the variance explained by the genic (intergenic) regions on each chromosome is also proportional to the total length of the genic (intergenic) regions (Figure 4).
Fig. 4. Estimates of the variance explained by all SNPs in genic (intergenic) regions averaged across 47 traits (all traits except INS0 and HOMA) against length of genic (intergenic) DNA. 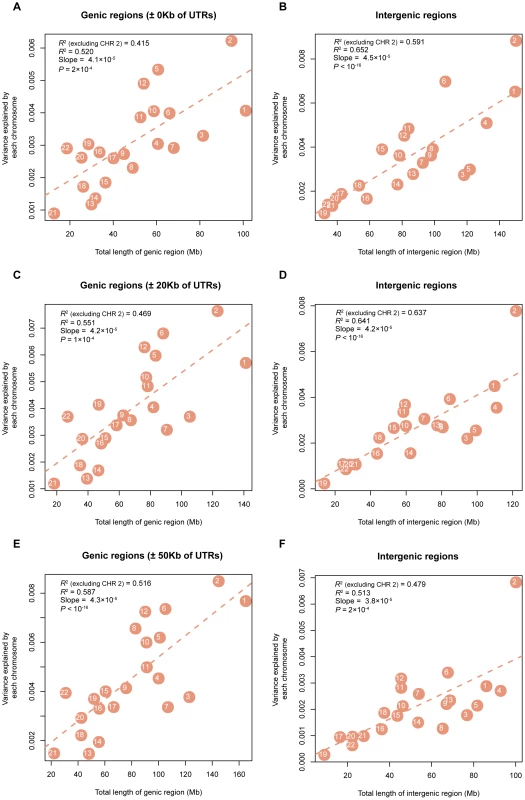
Shown on panels A), C) and E) are the results for the genic SNPs, and shown on panels B), D) and F) are the results for intergenic SNPs, under the three definitions of genic regions, ±0 Kb, ±20 Kb and ±50 Kb of UTRs, respectively. Discussion
Previous studies using the whole-genome estimation approach [10], [14] have shown that common SNPs explain a large proportion of heritability for traits and diseases such as height [10], [11], BMI [11], cognition ability [16], [17], rheumatoid arthritis [13] and schizophrenia [12]. The reason why GWAS have not yet identified all the common SNPs that explain this amount of variation is mainly because there are many of them each with an effect too small to pass the stringent genome-wide significance level. However, each of these studies focused only on one or a few diseases or traits. We estimated and partitioned the genetic variance that tagged by all common SNPs for 49 traits in an eastern Asian population and showed by a number of analyses that polygenic inheritance is ubiquitous for most human complex traits.
The estimates of for 6 traits, however, were not different from zero at the nominal significance level (0.05) and the estimates for two insulin related traits INS0 (fasting blood insulin level) and HOMA (homoeostasis model assessment for insulin resistance) were constrained at zero in the analysis because the estimates were converged at small negative values during the estimation process. It does not necessarily mean that common SNPs do not explain any genetic variance for INS0 and HOMA. It could mean that for the two traits are small and their estimates approached zero just because of random sampling. For example, if the true parameter of for a trait is 0.05, given a SE of 0.04 (similar magnitude as those presented in Table 1), the probability of getting a zero estimate of is approximately 0.11, meaning that it is not surprising to observe a few zero estimates from an analysis of 49 estimates if the true parameters of for these traits have a spectrum from moderate to small values.
The estimate of for height was 31.6% (SE = 4.6%), which was smaller than the estimate from a study in Australians ( = 44.9%, SE = 8.3%) [10] but not statistically significant (P = 0.161), and was significantly (P = 0.015) smaller than the estimate from another study in European Americans ( = 44.8%, SE = 2.9%) [11]. There could be two possible reasons: 1) there is a difference in heritability for height between Koreans and Europeans and 2) the tagging of Affymetrix 5.0 array is not as good as the later version Affymetrix 6.0 and the Illumina HumanCNV370 arrays used in the previous studies in Europeans. The estimate for BMI ( = 14.7%, SE = 4.1%) was also slightly smaller than that in European Americans ( = 16.5%, SE = 2.9%) [11] but the difference was not significant (P = 0.741). We estimated the narrow-sense heritability for 11 traits by from a family study in Koreans (Text S1 and Table S6). The estimate of heritability either for height (h2 = 0.744, SE = 0.048) or for BMI (h2 = 0.478, SE = 0.057) in Koreans was comparable to that estimated in Europeans. We then estimated the variance explained by all SNPs on Affymetrix 5.0 array in the sample of 11,586 unrelated European Americans as used in [11] (Text S1). The estimate of variance explained by all SNPs on Affymetrix 5.0 array in European Americans was 0.394 (SE = 0.027) for height, which was not significantly different from that estimated in this study (P = 0.118). Therefore, the difference between the estimate of in this study and in previous studies is partly due to the use of different types of SNP genotyping arrays and partly due to sampling error.
It is demonstrated by the genome partitioning analysis that there was a strong linear relationship between the estimates of variance explained by individual chromosomes and chromosome length (Figure 2). The correlation between variance explained and DNA length was stronger in the intergenic regions than that in the genic regions if we define the genic region as ±0 Kb or ±20 Kb of UTRs, while it was stronger in the genic regions than that in the intergenic regions if we define the genic region as ±50 Kb of UTRs (Figure 4). We show by a number of analyses that the result was driven neither by the difference between the number of SNPs in genic regions and in intergenic regions nor by the difference in MAF distribution between genic and intergeinc SNPs (Text S2). If trait-associated genetic variants are enriched in functional elements such as introns and UTRs and diluted in exons, the relationship between the variance explain and DNA length will be attenuated in the genic region. However, this could also be just due to sampling. The sampling variance of a regression R2 is approximately 4ρ2(1−ρ2)/N where E(R2) = ρ2 and N is number of observations (number of chromosomes in this case). Given ρ2 = 0.5 and N = 22, the SE of the regression R2 is ∼0.2. Therefore, the difference between the correlation (between the variance explained and DNA length) in genic regions and that in intergenic regions is unlikely to be significant. In addition, in the partitioning analysis of intergenic regions, chromosome 2 seems to be an outlier (Figure 4). For example, for the definition of genic region of ±50 Kb, the variance explained by the intergenic regions on chromosome 2 averaged across 47 traits was 0.68% (SE = ∼0.16%), which was 0.25% larger than the expected value from the fitted line. Given the SE of ∼0.16%, the difference was, however, not greater than what we would expect by chance (P = 0.118).
Moreover, we attempted to investigate the enrichment of genetic variants in genes involved in biological pathways. For any particular trait, there are a number of biological pathways that are important to the trait development. We chose the well-known insulin signal transduction pathway as an example to demonstrate the use of GCTA to partition the genetic variance based on functional annotations. We took SNPs that are ±20 kb away from 103 genes that are involved in insulin signaling pathway. There were 955 SNPs which covered ∼0.45% of the genome. We then performed the genome partitioning analysis to decompose into two components, i.e. the contribution of the genes involved in insulin pathway and that of the rest of the genome for 11 lipids and diabetes related traits. As shown in Table S7, we did not find any evidence that genes involved in insulin pathway explained disproportionally more proportion of variance. This is not surprising because these gene regions cover ∼0.45% of the genome and the SE of the estimate was ∼0.3% so that even if there is an enrichment of genetic variants in these gene regions, it is unable to be detected due to the lack of power. Larger sample size is required for such kind of analysis in the future.
In conclusion, we showed by whole genome estimation and partitioning analyses that, most human complex traits, if not all, appear to be highly polygenic, i.e. there are a large number of genetic variants segregating in the population with a small effect widely distributed across the whole genome. All the common SNPs on the Affymetrix 5.0 array explain approximately a third of heritability on average over all the 49 traits analysed in this study. The remaining unexplained two thirds of heritability could be due to causal variants including the common and rare ones that are not well tagged by SNPs on the array or possibly due to the heritability was over-estimated in the family/twin studies. The conclusion drawn from previous studies that heritability is not missing but due to many variants with small effects is not specific for human height in European populations but likely to be in common for most human complex traits and populations. Taken all together, it implies that although whole genome sequencing data will provide much denser genomic coverage than the current genotyping array and will therefore identify more associated variants and explain more genetic variance, large sample size is still essential.
Materials and Methods
The KARE cohort
This study used the data from the Korea Association Resource (KARE) project, which has been described elsewhere [15]. In brief, there were 10,038 individuals recruited from two community-based cohorts, 5,018 from Ansung and 5,020 from Ansan, in Gyeonggi Province, South Korea. The individuals were aged from 40 to 69 years old and born in 1931 to 1963. All the individuals were measured for a range of quantitative traits through epidemiological surveys, physical examinations and laboratory tests, including traits related to obesity, blood condition, pulse, bone mineral density, lipids, diabetes index, liver functions, lung functions and kidney functions. A description of the 49 traits used in this study is summarized in Table S1. We adjusted the phenotypes of each trait for age by simple regression and then standardized the residuals to z-scores, in each of the two cohorts (Ansung and Ansan) and in each gender group separately.
Genotyped and imputed data
The genomic DNAs were isolated from peripheral blood drawn from the participants and were genotyped with 500,568 SNPs on the Affymetrix 5.0 genotyping array [15]. We excluded the SNPs with missingness rate >5%, minor allele frequency (MAF)<0.01, and Hardy-Weinberg equilibrium (HWE) test P value<10−6 using PLINK [18], and retained 326,262 autosomal SNPs for further analysis. The KARE GWAS data had been imputed to HapMap2 CHB and JPT panels [19]. After removing SNPs with MAF<0.01 and SNP missing rate >0.05, there were 2,153,258 genotyped/imputed SNPs [15].
Estimating and partitioning genetic variance using SNP data
We estimated the genetic relationship matrix (GRM) between all pairs of individuals from all the genotyped SNPs and excluded one of each pair of individuals with estimated relationship >0.025 retaining 7,170 unrelated individuals. For each trait, we then estimated the variance that can be captured by all SNPs using the restricted maximum likelihood (REML) approach in mixed linear model , where y is a vector of phenotypes, b is a vector of fixed effects with its incidence matrix X, is a vector of aggregate effects of all SNPs, and with AG being the SNP-derived GRM and being the additive genetic variance. The proportion of variance explained by all SNPs is defined as with being the phenotypic variance. Details of the model and parameter estimation have been described elsewhere [10], [14]. In addition, using the same method as above but allowing to fit multiple genetic components simultaneously in the model, we partitioned into the contributions of genic () and intergenic () regions of the whole genome [11] and averaged the estimates of and across all the traits. The genic regions were defined as ±0 kb, ±20 kb and ±50 kb of the 3′ and 5′ UTRs. A total of 135,491, 175,637 and 205,901 SNPs were located within the boundaries of 12,310, 15,140 and 15,274 protein-coding genes for the three definitions (±0 kb, ±20 kb and ±50 kb), respectively, which covered 36.1%, 49.2% and 58.9% of the genome.
Supporting Information
Zdroje
1. HindorffLA, SethupathyP, JunkinsHA, RamosEM, MehtaJP, et al. (2009) Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc Natl Acad Sci USA 106 : 9362–9367.
2. VisscherPM, BrownMA, McCarthyMI, YangJ (2012) Five years of GWAS discovery. Am J Hum Genet 90 : 7–24.
3. ManolioTA, CollinsFS, CoxNJ, GoldsteinDB, HindorffLA, et al. (2009) Finding the missing heritability of complex diseases. Nature 461 : 747–753.
4. MaherB (2008) Personal genomes: The case of the missing heritability. Nature 456 : 18–21.
5. Lango AllenH, EstradaK, LettreG, BerndtSI, WeedonMN, et al. (2010) Hundreds of variants clustered in genomic loci and biological pathways affect human height. Nature 467 : 832–838.
6. SpeliotesEK, WillerCJ, BerndtSI, MondaKL, ThorleifssonG, et al. (2010) Association analyses of 249,796 individuals reveal 18 new loci associated with body mass index. Nat Genet 42 : 937–948.
7. VisscherPM, HillWG, WrayNR (2008) Heritability in the genomics era–concepts and misconceptions. Nat Rev Genet 9 : 255–266.
8. MagnussonPK, RasmussenF (2002) Familial resemblance of body mass index and familial risk of high and low body mass index. A study of young men in Sweden. Int J Obes Relat Metab Disord 26 : 1225–1231.
9. SchousboeK, WillemsenG, KyvikKO, MortensenJ, BoomsmaDI, et al. (2003) Sex differences in heritability of BMI: a comparative study of results from twin studies in eight countries. Twin Res 6 : 409–421.
10. YangJ, BenyaminB, McEvoyBP, GordonS, HendersAK, et al. (2010) Common SNPs explain a large proportion of the heritability for human height. Nat Genet 42 : 565–569.
11. YangJ, ManolioTA, PasqualeLR, BoerwinkleE, CaporasoN, et al. (2011) Genome partitioning of genetic variation for complex traits using common SNPs. Nat Genet 43 : 519–525.
12. LeeSH, DecandiaTR, RipkeS, YangJ, SullivanPF, et al. (2012) Estimating the proportion of variation in susceptibility to schizophrenia captured by common SNPs. Nat Genet 44 : 247–250.
13. StahlEA, WegmannD, TrynkaG, Gutierrez-AchuryJ, DoR, et al. (2012) Bayesian inference analyses of the polygenic architecture of rheumatoid arthritis. Nat Genet 44 : 483–489.
14. YangJ, LeeSH, GoddardME, VisscherPM (2011) GCTA: a tool for genome-wide complex trait analysis. Am J Hum Genet 88 : 76–82.
15. ChoYS, GoMJ, KimYJ, HeoJY, OhJH, et al. (2009) A large-scale genome-wide association study of Asian populations uncovers genetic factors influencing eight quantitative traits. Nat Genet 41 : 527–534.
16. DaviesG, TenesaA, PaytonA, YangJ, HarrisSE, et al. (2011) Genome-wide association studies establish that human intelligence is highly heritable and polygenic. Mol Psychiatry 16 : 996–1005.
17. DearyIJ, YangJ, DaviesG, HarrisSE, TenesaA, et al. (2012) Genetic contributions to stability and change in intelligence from childhood to old age. Nature 482 : 212–215.
18. PurcellS, NealeB, Todd-BrownK, ThomasL, FerreiraMA, et al. (2007) PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet 81 : 559–575.
19. The International HapMap Consortium (2007) A second generation human haplotype map of over 3.1 million SNPs. Nature 449 : 851–861.
20. AltshulerDM, GibbsRA, PeltonenL, AltshulerDM, GibbsRA, et al. (2010) Integrating common and rare genetic variation in diverse human populations. Nature 467 : 52–58.
Štítky
Genetika Reprodukční medicína
Článek Alternative Splicing and Subfunctionalization Generates Functional Diversity in Fungal ProteomesČlánek RFX Transcription Factor DAF-19 Regulates 5-HT and Innate Immune Responses to Pathogenic Bacteria inČlánek Surveillance-Activated Defenses Block the ROS–Induced Mitochondrial Unfolded Protein ResponseČlánek Deficiency Reduces Adipose OXPHOS Capacity and Triggers Inflammation and Insulin Resistance in Mice
Článek vyšel v časopisePLOS Genetics
Nejčtenější tento týden
2013 Číslo 3- IVF a rakovina prsu – zvyšují hormony riziko vzniku rakoviny?
- Akutní intermitentní porfyrie
- Souvislost haplotypu M2 genu pro annexin A5 s opakovanými reprodukčními ztrátami
- Transthyretinová amyloidóza z pohledu neurologa a kardiologa aneb jak se vyhnout „misdiagnostice“?
- Hypogonadotropní hypogonadismus u žen a vliv na výsledky reprodukce po IVF
-
Všechny články tohoto čísla
- Power and Predictive Accuracy of Polygenic Risk Scores
- Rare Copy Number Variants Are a Common Cause of Short Stature
- Coordination of Flower Maturation by a Regulatory Circuit of Three MicroRNAs
- Ubiquitous Polygenicity of Human Complex Traits: Genome-Wide Analysis of 49 Traits in Koreans
- Genomic Evidence for Island Population Conversion Resolves Conflicting Theories of Polar Bear Evolution
- Mechanistic Insight into the Pathology of Polyalanine Expansion Disorders Revealed by a Mouse Model for X Linked Hypopituitarism
- Genome-Wide Association Study and Gene Expression Analysis Identifies as a Predictor of Response to Etanercept Therapy in Rheumatoid Arthritis
- Problem Solved: An Interview with Sir Edwin Southern
- Long Interspersed Element–1 (LINE-1): Passenger or Driver in Human Neoplasms?
- Mouse HFM1/Mer3 Is Required for Crossover Formation and Complete Synapsis of Homologous Chromosomes during Meiosis
- Alternative Splicing and Subfunctionalization Generates Functional Diversity in Fungal Proteomes
- A WRKY Transcription Factor Recruits the SYG1-Like Protein SHB1 to Activate Gene Expression and Seed Cavity Enlargement
- Microhomology-Mediated Mechanisms Underlie Non-Recurrent Disease-Causing Microdeletions of the Gene or Its Regulatory Domain
- Ancient Evolutionary Trade-Offs between Yeast Ploidy States
- Differential Evolutionary Fate of an Ancestral Primate Endogenous Retrovirus Envelope Gene, the EnvV , Captured for a Function in Placentation
- A Feed-Forward Loop Coupling Extracellular BMP Transport and Morphogenesis in Wing
- The Tomato Yellow Leaf Curl Virus Resistance Genes and Are Allelic and Code for DFDGD-Class RNA–Dependent RNA Polymerases
- The U-Box E3 Ubiquitin Ligase TUD1 Functions with a Heterotrimeric G α Subunit to Regulate Brassinosteroid-Mediated Growth in Rice
- Role of the DSC1 Channel in Regulating Neuronal Excitability in : Extending Nervous System Stability under Stress
- –Independent Phenotypic Switching in and a Dual Role for Wor1 in Regulating Switching and Filamentation
- Pax6 Regulates Gene Expression in the Vertebrate Lens through miR-204
- Blood-Informative Transcripts Define Nine Common Axes of Peripheral Blood Gene Expression
- Genetic Architecture of Skin and Eye Color in an African-European Admixed Population
- Fine Characterisation of a Recombination Hotspot at the Locus and Resolution of the Paradoxical Excess of Duplications over Deletions in the General Population
- Estrogen Mediated-Activation of miR-191/425 Cluster Modulates Tumorigenicity of Breast Cancer Cells Depending on Estrogen Receptor Status
- Complex Patterns of Genomic Admixture within Southern Africa
- Yap- and Cdc42-Dependent Nephrogenesis and Morphogenesis during Mouse Kidney Development
- Molecular Networks of Human Muscle Adaptation to Exercise and Age
- Alp/Enigma Family Proteins Cooperate in Z-Disc Formation and Myofibril Assembly
- Polycomb Group Gene Regulates Rice () Seed Development and Grain Filling via a Mechanism Distinct from
- RFX Transcription Factor DAF-19 Regulates 5-HT and Innate Immune Responses to Pathogenic Bacteria in
- Distinct Molecular Strategies for Hox-Mediated Limb Suppression in : From Cooperativity to Dispensability/Antagonism in TALE Partnership
- A Natural Polymorphism in rDNA Replication Origins Links Origin Activation with Calorie Restriction and Lifespan
- TDP2–Dependent Non-Homologous End-Joining Protects against Topoisomerase II–Induced DNA Breaks and Genome Instability in Cells and
- Recurrent Rearrangement during Adaptive Evolution in an Interspecific Yeast Hybrid Suggests a Model for Rapid Introgression
- Genome-Wide Association Study in Mutation Carriers Identifies Novel Loci Associated with Breast and Ovarian Cancer Risk
- Coincident Resection at Both Ends of Random, γ–Induced Double-Strand Breaks Requires MRX (MRN), Sae2 (Ctp1), and Mre11-Nuclease
- Identification of a -Specific Modifier Locus at 6p24 Related to Breast Cancer Risk
- A Novel Function for the Hox Gene in the Male Accessory Gland Regulates the Long-Term Female Post-Mating Response in
- Tdp2: A Means to Fixing the Ends
- A Novel Role for the RNA–Binding Protein FXR1P in Myoblasts Cell-Cycle Progression by Modulating mRNA Stability
- Association Mapping and the Genomic Consequences of Selection in Sunflower
- Histone Deacetylase 2 (HDAC2) Regulates Chromosome Segregation and Kinetochore Function via H4K16 Deacetylation during Oocyte Maturation in Mouse
- A Novel Mutation in the Upstream Open Reading Frame of the Gene Causes a MEN4 Phenotype
- Ataxin1L Is a Regulator of HSC Function Highlighting the Utility of Cross-Tissue Comparisons for Gene Discovery
- Human Spermatogenic Failure Purges Deleterious Mutation Load from the Autosomes and Both Sex Chromosomes, including the Gene
- A Conserved Upstream Motif Orchestrates Autonomous, Germline-Enriched Expression of piRNAs
- Statistical Analysis Reveals Co-Expression Patterns of Many Pairs of Genes in Yeast Are Jointly Regulated by Interacting Loci
- Matefin/SUN-1 Phosphorylation Is Part of a Surveillance Mechanism to Coordinate Chromosome Synapsis and Recombination with Meiotic Progression and Chromosome Movement
- A Role for the Malignant Brain Tumour (MBT) Domain Protein LIN-61 in DNA Double-Strand Break Repair by Homologous Recombination
- The Population and Evolutionary Dynamics of Phage and Bacteria with CRISPR–Mediated Immunity
- Long Noncoding RNA MALAT1 Controls Cell Cycle Progression by Regulating the Expression of Oncogenic Transcription Factor B-MYB
- Surveillance-Activated Defenses Block the ROS–Induced Mitochondrial Unfolded Protein Response
- DNA Topoisomerase III Localizes to Centromeres and Affects Centromeric CENP-A Levels in Fission Yeast
- Genome-Wide Control of RNA Polymerase II Activity by Cohesin
- Divergent Selection Drives Genetic Differentiation in an R2R3-MYB Transcription Factor That Contributes to Incipient Speciation in
- NODULE INCEPTION Directly Targets Subunit Genes to Regulate Essential Processes of Root Nodule Development in
- Spreading of a Prion Domain from Cell-to-Cell by Vesicular Transport in
- Deficiency in Origin Licensing Proteins Impairs Cilia Formation: Implications for the Aetiology of Meier-Gorlin Syndrome
- Deficiency Reduces Adipose OXPHOS Capacity and Triggers Inflammation and Insulin Resistance in Mice
- The Conserved SKN-1/Nrf2 Stress Response Pathway Regulates Synaptic Function in
- Functional Genomic Analysis of the Regulatory Network in
- Astakine 2—the Dark Knight Linking Melatonin to Circadian Regulation in Crustaceans
- CRL2 E3-Ligase Regulates Proliferation and Progression through Meiosis in the Germline
- Both the Caspase CSP-1 and a Caspase-Independent Pathway Promote Programmed Cell Death in Parallel to the Canonical Pathway for Apoptosis in
- PRMT4 Is a Novel Coactivator of c-Myb-Dependent Transcription in Haematopoietic Cell Lines
- A Copy Number Variant at the Locus Likely Confers Risk for Canine Squamous Cell Carcinoma of the Digit
- Evidence of Gene–Environment Interactions between Common Breast Cancer Susceptibility Loci and Established Environmental Risk Factors
- HIV Infection Disrupts the Sympatric Host–Pathogen Relationship in Human Tuberculosis
- Trans-Ethnic Fine-Mapping of Lipid Loci Identifies Population-Specific Signals and Allelic Heterogeneity That Increases the Trait Variance Explained
- A Gene Transfer Agent and a Dynamic Repertoire of Secretion Systems Hold the Keys to the Explosive Radiation of the Emerging Pathogen
- The Role of ATM in the Deficiency in Nonhomologous End-Joining near Telomeres in a Human Cancer Cell Line
- Dynamic Circadian Protein–Protein Interaction Networks Predict Temporal Organization of Cellular Functions
- Nuclear Myosin 1c Facilitates the Chromatin Modifications Required to Activate rRNA Gene Transcription and Cell Cycle Progression
- Robust Prediction of Expression Differences among Human Individuals Using Only Genotype Information
- A Single Cohesin Complex Performs Mitotic and Meiotic Functions in the Protist
- The Role of the Arabidopsis Exosome in siRNA–Independent Silencing of Heterochromatic Loci
- Elevated Expression of the Integrin-Associated Protein PINCH Suppresses the Defects of Muscle Hypercontraction Mutants
- Twist1 Controls a Cell-Specification Switch Governing Cell Fate Decisions within the Cardiac Neural Crest
- Genome-Wide Testing of Putative Functional Exonic Variants in Relationship with Breast and Prostate Cancer Risk in a Multiethnic Population
- Heteroduplex DNA Position Defines the Roles of the Sgs1, Srs2, and Mph1 Helicases in Promoting Distinct Recombination Outcomes
- PLOS Genetics
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Fine Characterisation of a Recombination Hotspot at the Locus and Resolution of the Paradoxical Excess of Duplications over Deletions in the General Population
- Molecular Networks of Human Muscle Adaptation to Exercise and Age
- Recurrent Rearrangement during Adaptive Evolution in an Interspecific Yeast Hybrid Suggests a Model for Rapid Introgression
- Genome-Wide Association Study and Gene Expression Analysis Identifies as a Predictor of Response to Etanercept Therapy in Rheumatoid Arthritis
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání



