-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaSelection of Resistant Bacteria at Very Low Antibiotic Concentrations
The widespread use of antibiotics is selecting for a variety of resistance mechanisms that seriously challenge our ability to treat bacterial infections. Resistant bacteria can be selected at the high concentrations of antibiotics used therapeutically, but what role the much lower antibiotic concentrations present in many environments plays in selection remains largely unclear. Here we show using highly sensitive competition experiments that selection of resistant bacteria occurs at extremely low antibiotic concentrations. Thus, for three clinically important antibiotics, drug concentrations up to several hundred-fold below the minimal inhibitory concentration of susceptible bacteria could enrich for resistant bacteria, even when present at a very low initial fraction. We also show that de novo mutants can be selected at sub-MIC concentrations of antibiotics, and we provide a mathematical model predicting how rapidly such mutants would take over in a susceptible population. These results add another dimension to the evolution of resistance and suggest that the low antibiotic concentrations found in many natural environments are important for enrichment and maintenance of resistance in bacterial populations.
Published in the journal: . PLoS Pathog 7(7): e32767. doi:10.1371/journal.ppat.1002158
Category: Research Article
doi: https://doi.org/10.1371/journal.ppat.1002158Summary
The widespread use of antibiotics is selecting for a variety of resistance mechanisms that seriously challenge our ability to treat bacterial infections. Resistant bacteria can be selected at the high concentrations of antibiotics used therapeutically, but what role the much lower antibiotic concentrations present in many environments plays in selection remains largely unclear. Here we show using highly sensitive competition experiments that selection of resistant bacteria occurs at extremely low antibiotic concentrations. Thus, for three clinically important antibiotics, drug concentrations up to several hundred-fold below the minimal inhibitory concentration of susceptible bacteria could enrich for resistant bacteria, even when present at a very low initial fraction. We also show that de novo mutants can be selected at sub-MIC concentrations of antibiotics, and we provide a mathematical model predicting how rapidly such mutants would take over in a susceptible population. These results add another dimension to the evolution of resistance and suggest that the low antibiotic concentrations found in many natural environments are important for enrichment and maintenance of resistance in bacterial populations.
Introduction
Antibiotics represent one of mankind's most important medical inventions but during the last decades the continuing rapid development of antibiotic resistance has emerged as one of the most serious health care problems, both in community and hospital settings [1], [2], [3]. Whereas some resistance-conferring genes were most likely originally selected to serve metabolic functions and/or for signal trafficking or protection against competing antibiotic-producing bacteria [4], the recent worldwide enrichment and spread of highly resistant pathogenic bacteria in the micro-biosphere has largely been driven by human activities, including the extensive use and misuse of antibiotics in human and veterinary medicine and in agriculture [2], [3], [5], [6], [7]. While it is evident that the high concentrations of antibiotics used therapeutically can select for resistant mutants, it still remains unclear how important the low antibiotic concentrations that due to anthropogenic input pollute natural (e.g. aquatic or soil) environments [8], [9], [10], that are produced naturally by antibiotic-producing micro-organisms or that are present in certain human/animal body compartments during therapeutic or growth promotion use, are for the selection and enrichment of resistant mutants. In pharmacodynamic models it is generally assumed that selection of resistant bacteria only occurs at concentrations between the minimal inhibitory concentration (MIC) of the susceptible wild type population (MICsusc) and that of the resistant bacteria (MICres) [11], [12] (mutant selective window hypothesis, see Fig. 1A) and that concentrations below the MICsusc will not inhibit growth of the susceptible bacteria and therefore not be selective. Earlier studies on selection with small differences in bacterial susceptibility to antibiotics show that selection can efficiently act on minute differences to select for resistance [13], [14], [15]. Furthermore, using an elegant color-based assay a recent study has shown qualitatively that levels of antibiotics below the MIC can enrich for resistant bacteria [16]. Here, we further explore the mutant selective window assumption and as outlined schematically in Fig. 1A, we examine for two bacterial species and three antibiotics how far below the MICsusc pre-existing and de novo generated resistant mutants can be selectively enriched because of minute reductions in the growth rate of their susceptible counterparts.
Fig. 1. Growth rates as a function of antibiotic concentration. 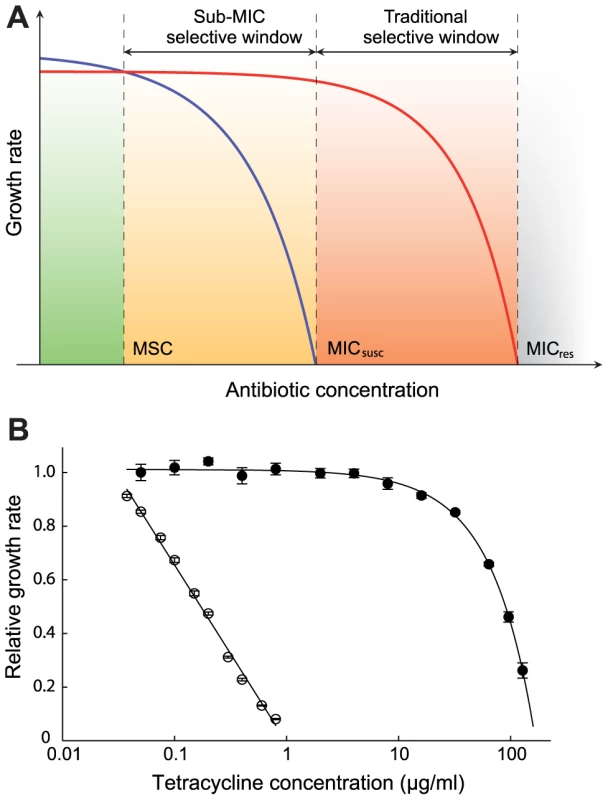
(A) Schematic representation of growth rates as a function of antibiotic concentration. Green indicates a concentration interval where the susceptible strain (blue line) will outcompete the resistant strain (red line). Orange (sub-MIC selective window) and red (traditional mutant selective window) indicate concentration intervals where the resistant strain will outcompete the susceptible strain. MICsusc = minimal inhibitory concentration of the susceptible strain, MICres = minimal inhibitory concentration of the resistant strain and MSC = minimal selective concentration. (B). Relative exponential growth rates of susceptible (open circles) and resistant (closed circles) strains of S. typhimurium as a function of tetracycline concentration. Standard errors of the mean are indicated. A relative growth rate of 1.0 corresponds to approximately 1.8 hr−1. Cells were grown in Mueller Hinton medium at 37°C. To determine if exposure to very low antibiotic concentrations (<<MICsusc) can result in enrichment for resistant mutants, we used several well-defined mutants of Escherichia coli and Salmonella enterica (Var. Typhimurium LT2) (Table S1 in Text S1) and three different classes of antibiotics with high importance to human and veterinary medicine (tetracyclines, fluoroquinolones and aminoglycosides). The resistance markers used were Tn10dTet (confers tetracycline resistance), gyrA (S83L and D87N), ΔmarR, and ΔacrR mutations (confer ciprofloxacin resistance) and rpsL (K42R) (confers streptomycin resistance), all of which are found in clinical isolates of several different bacterial species. Using highly sensitive competition experiments between isogenic pairs of susceptible and resistant strains, we show that selection of resistant bacteria can occur at antibiotic concentrations far below the minimal inhibitory concentration. Finally, we present a mathematical model, showing how resistant mutants are expected to arise de novo and spread in bacterial populations at these sub-MIC levels of antibiotics.
Results
An initial examination of the effect of low antibiotic concentrations was performed in single cultures where a susceptible wild-type and a resistant mutant carrying a Tn10dTet were grown separately in the presence of different concentrations of tetracycline. As shown in Fig. 1B and Table S2 in Text S1, concentrations far below MICsusc reduced the exponential growth rate of the susceptible strain without any apparent effect on the resistant strain. For example, at a concentration 1/30 of the MICsusc, the susceptible strain grew about 15% slower than without antibiotic whereas the resistant mutant seemed unaffected, suggesting that resistant strains are strongly selected at these low concentrations. To increase the sensitivity of these assays and allow detection of extremely small differences in growth rates, we performed competition experiments between pairs of susceptible and resistant strains. The MICs for the susceptible and resistant mutants were: S. typhimurium wild type (streptomycin = 4 ug/ml, tetracycline = 1.5 ug/ml), rpsL K42R >1024 ug/ml and Tn10dTet strain = 128 ug/ml; E. coli wild type (ciprofloxacin = 0.023 ug/ml), gyrA S83L (ciprofloxacin = 0.38 ug/ml), gyrA D87N (ciprofloxacin = 0.25 ug/ml), ΔacrR (ciprofloxacin = 0.047 ug/ml) and ΔmarR (ciprofloxacin = 0.047 ug/ml). The strains were genetically tagged with variants of the green fluorescent protein gene (yfp and cfp, encoding yellow - and cyan-fluorescent proteins, respectively) to allow counting of large populations of competing cells by fluorescence activated cell sorting (FACS), thereby significantly reducing any experimental errors associated with counting of small populations. The competing strains were isogenic except for the resistance determinant and the yfp and cfp genes producing the respective fluorescent proteins. Control experiments showed that the difference in fitness cost between the cfp and yfp markers had a negligible impact on growth rates (Fig. S1). The strains were competed for up to 80 generations by serial passage in batch cultures in the presence of different concentrations of either one of the antibiotics tetracycline, ciprofloxacin (a fluoroquinolone) and streptomycin (an aminoglycoside) as well as in the absence of drug (Fig. 2A–D, Fig. 3A–H, Fig. 4A–E). As shown by our previous studies [17], this experimental set-up allows detection of growth rate differences at least as small as 0.3%, which approaches the limit of sensitivity set by the interference of periodic selection events. Whereas the growth rate measurement shown in Fig. 1B only measured the exponential phase of growth, the competition experiments represent a composite of growth and survival in lag phase, exponential phase and stationary phase that allows examination of the whole growth cycle.
Fig. 2. Competition experiments between susceptible and resistant strains, streptomycin and tetracycline. 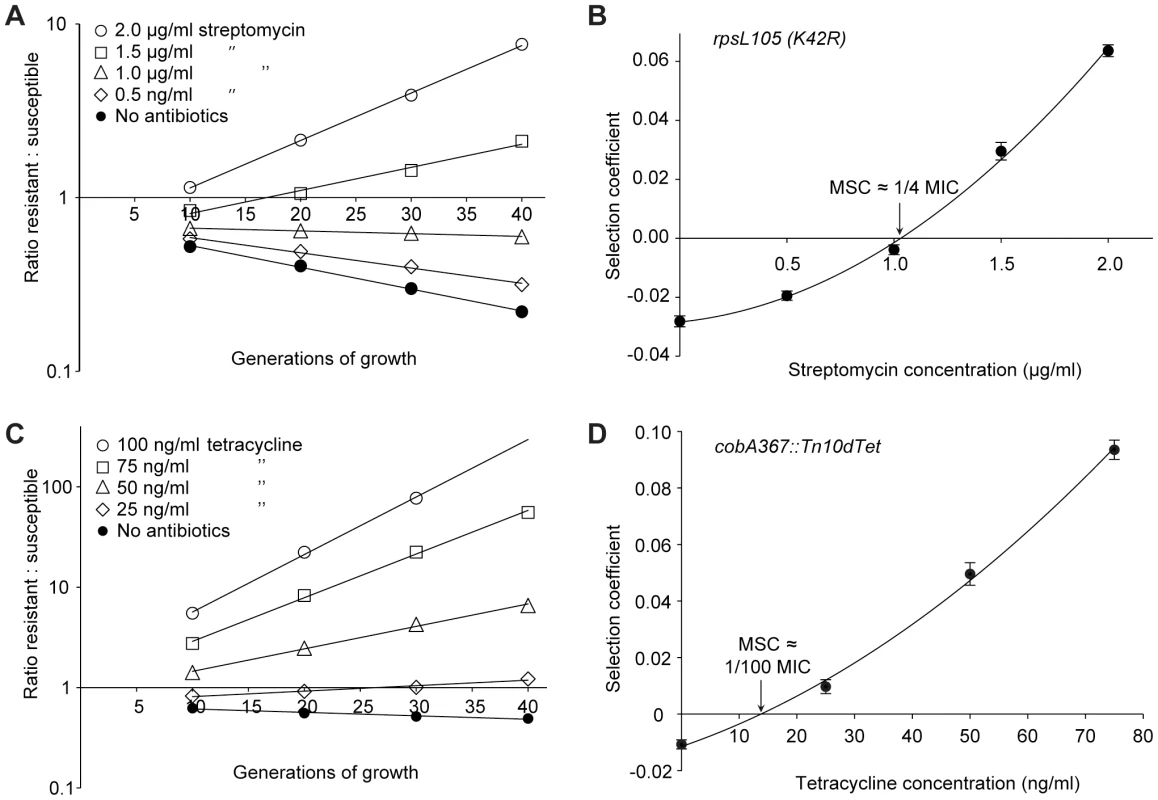
Competition experiments at different concentrations of antibiotics (A (rpsL105 (K42R)) and C (Tn10dtet), and calculated selection coefficients as a function of antibiotic concentrations (B and D). Fig. A and C are each based on one single competition experiment (averages of four competitions), while Fig. B and D are calculated from the selection coefficients of up to 20 competitions (Table S3 in Text S1). Standard errors of the mean are indicated. Fig. 3. Competition experiments between susceptible and resistant strains, ciprofloxacin. 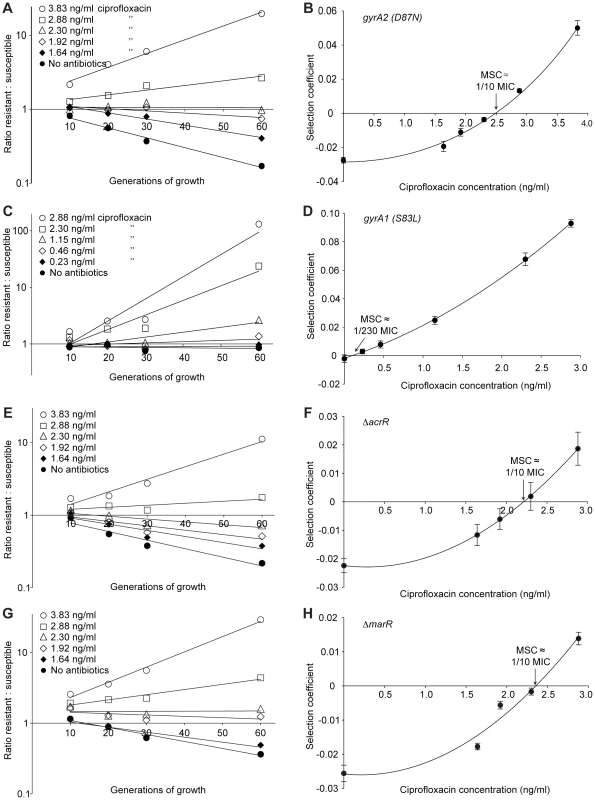
Competition experiments at different concentrations of ciprofloxacin (A (gyrA2 (D87N)), C (gyrA1 (S83L)), E (ΔacrR) and G (ΔmarR)) and calculated selection coefficients as a function of antibiotic concentrations (B, D, F and H). Fig. A, C, E and G are each based on one single competition experiment (averages of three competitions), while fig. B, D, F and H are calculated from the selection coefficients of 6 competitions (Table S3 in Text S1). Standard errors of the mean are indicated. Fig. 4. Competition experiments with low initial frequencies of resistant mutants. 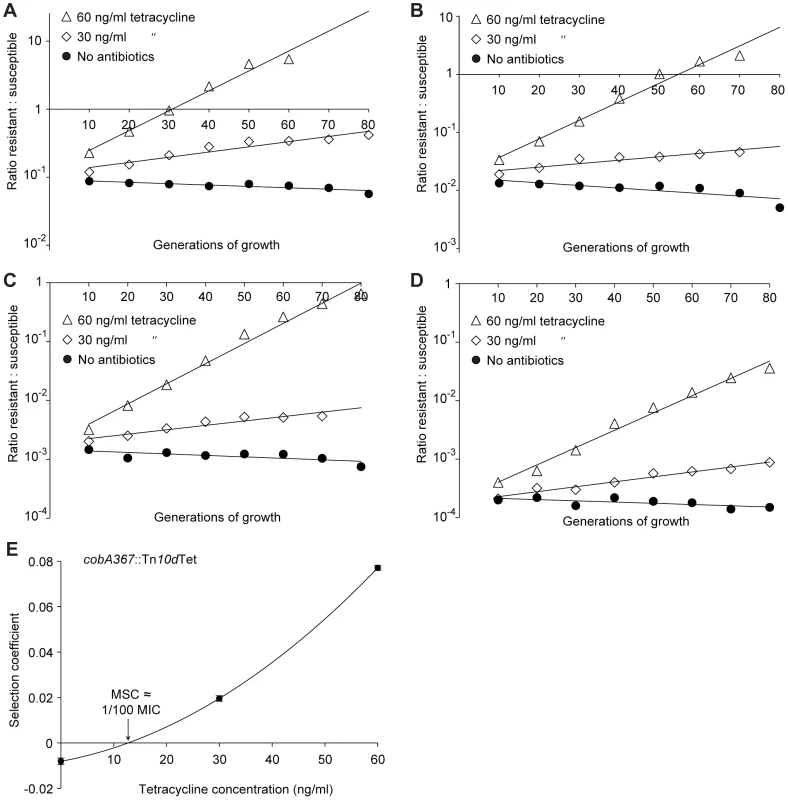
Competition experiments at different concentrations of antibiotics and different starting fractions of resistant mutants. (A) Initial ratio of susceptible to resistant mutants 10∶1. (B) Initial ratio of susceptible to resistant mutants 102∶1. (C) Initial ratio of susceptible to resistant mutants 103∶1. (D) Initial ratio of susceptible to resistant mutants 104∶1. (E) Calculated selection coefficients as a function of antibiotic concentrations. Fig. A to D are each based on one single competition experiment while E is calculated from the selection coefficients of 24 independent competitions with four different starting fractions of resistant mutants (Table S3 in Text S1). Standard errors of the mean are indicated. The data presented in Fig. 2A, C, Fig. 3A, C, E, G and Fig. 4A–D shows how the ratio of resistant:susceptible strains changes as a function of the number of generations of growth at different concentrations of antibiotic. Each line represents one competition experiment and the slope is a measure of the selection coefficient (s-value). Thus, the negative slope obtained in the absence of antibiotic is a measure of the fitness cost of the antibiotic resistance mechanism and a positive slope indicates that the resistant mutant is enriched. When the s-values obtained from these experiments are plotted as a function of antibiotic concentration the intercept, s = 0, represents what we specify as the minimal selective concentration (MSC) where the fitness cost of the resistance is balanced by the antibiotic-conferred selection for the resistant mutant (Fig. 2B, D, Fig. 3B, D, F, H and Fig. 4E). Depending on the antibiotic and the type of resistance mutation examined the MSC varied between 1/4 and 1/230 of the MICsusc. For streptomycin the MSC value was 1/4 of the MIC value of the susceptible strain (Fig. 2B), for tetracycline 1/100 (Fig. 2D) and for ciprofloxacin it varied between 1/10 (Fig. 3B) and 1/230 (Fig. 3D) of the MICsusc depending on the particular resistance mutation. These values correspond to absolute antibiotic concentrations of 1 µg/ml (streptomycin), 15 ng/ml (tetracycline), and 2.5 ng/ml to 100 pg/ml (ciprofloxacin). The competitions performed with a small initial fraction of resistant mutants also showed that the selection coefficients are independent of the initial frequency of resistant mutants. Even at initial frequencies as low as 10−4, the same enrichment (i.e. same selection coefficient) of the resistant mutants could be observed as at a 1∶1 ratio (compare Figures 2D and 4E).
Since the resistant mutants could be enriched from very low initial fractions (10−4) we also tested whether resistant mutants could be selected de novo from a susceptible population. To this end we grew 20 independent lineages of a susceptible wild type Salmonella typhimurium LT2 strain for 700 generations at 1/4 of the MIC of streptomycin and continuously screened for resistant cells by plating on different concentrations of streptomycin. At this low level of antibiotic we could observe rapid enrichment of de novo resistant mutants (Fig. 5). Thus, within 200 to 400 generations, a considerable enrichment of mutants with resistances between 2 and 16 times the MIC of the starting strain (8–64 µg/ml) could be seen, and after 500 to 600 generations also high-level resistant mutants (24–32 times MIC of the wild type = 96–128 µg/ml) appeared. After 400 generations, all 20 lineages contained subpopulations with a MIC higher than 32 µg/ml (8 times MIC), and after 600 generations 14 of the lineages had subpopulations with a MIC higher than 64 µg/ml (16 times MIC). Using the method described above, 20 lineages of wild type E. coli were grown for 600 generations in sub-MIC levels of ciprofloxacin. After 500 generations of growth at 1/10 of the MIC, five of the lineages had subpopulations (>1% of the population) with low level resistance (2-fold higher MIC than the susceptible parental strain) to ciprofloxacin, and after 600 generations, one out of twenty lineages had a subpopulation of cells with an MIC 8-fold higher than the susceptible parental strain (see Fig. S2).
Fig. 5. Selection of de novo resistant mutants at sub-inhibitory concentrations of antibiotics. 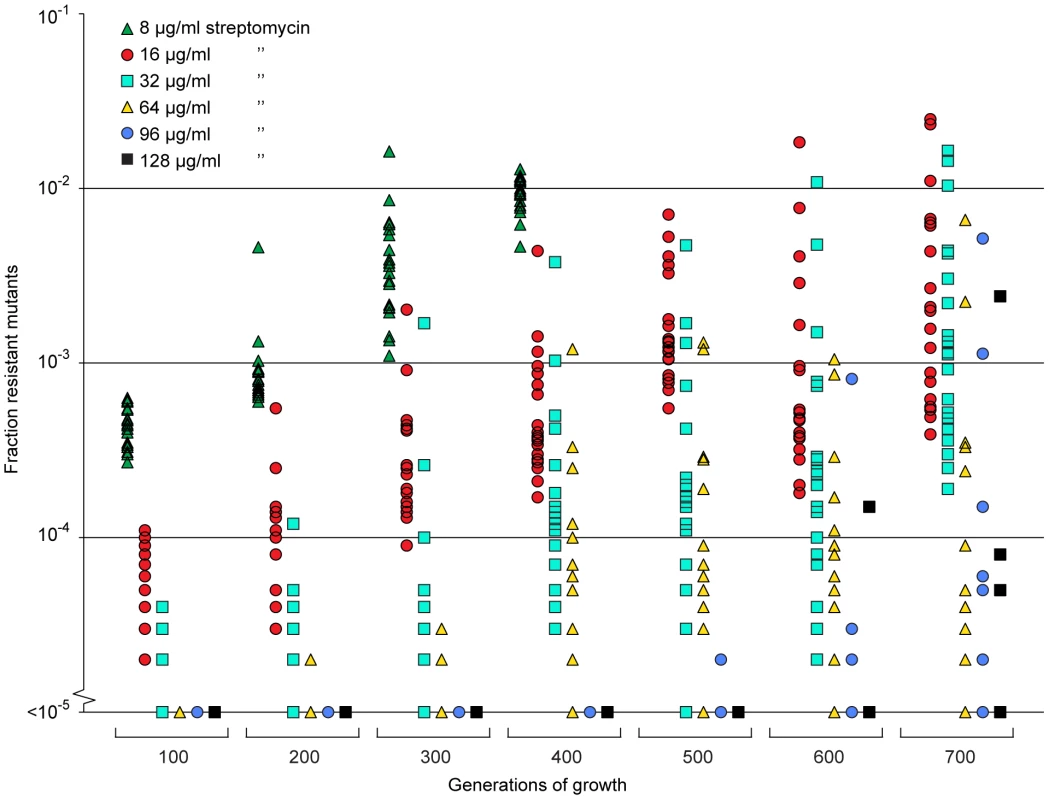
A total of 20 independent lineages of S. typhimurium were serially passaged in Mueller-Hinton medium containing 1 µg/ml streptomycin. Every 100 generations approximately 105 cells were plated onto LB agar containing different concentrations of streptomycin and the fractions of resistant mutants were calculated. The data points are grouped by number of generations of growth and resistance level, and in each of these data sets one data point represents the fraction of cells present in one lineage capable of growth at the specified antibiotic concentrations. Please note that data points at the baseline will overlap. We also calculated (Appendix in Text S1) how rapidly de novo generated resistant mutants would take over in a susceptible population at low antibiotic concentration, as determined by mutation rates (u), population sizes (N), and the fitness advantage (s) in the presence of antibiotics. s depends on the antibiotic concentration above the MSC as shown in Fig. 2 and 3. When no resistance mutants are present initially, the time to fixation can be expressed as
The first term is the stochastic waiting time for the first surviving mutant to appear and the second term is from the subsequent growth to 50% presence. For small values of uN <0.1, the first term dominates and fixation may be slow. For large values, uN >1, the second term dominates and fixation can be fast, ca. 100–1000 generations for s between 0.1–0.01 (Fig. 6). In this limit, resistance mutants appear so frequently that it makes little difference to the fixation time if they are present initially or not. In this context it is worth noting that sub-MIC levels of several antibiotics, most pronounced for fluoroquinolones, have been shown to increase bacterial mutation rates which potentially could reduce the waiting time and thereby increase the rate of mutant take-over [18].
Fig. 6. Fixation time for adaptive mutations. 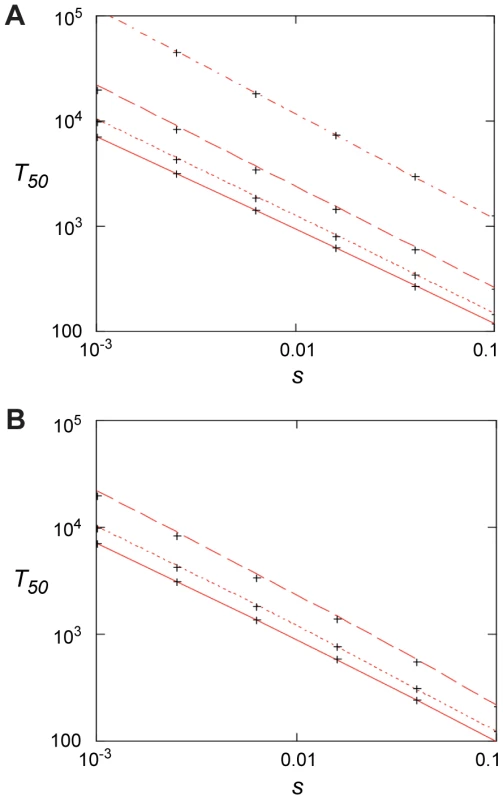
(A) 50% penetration time as function of selection coefficient when no mutants are present initially for N = 107 and, from top to bottom, u = 10−9, 10−8, 10−7, and 10−6. Red lines are from Eq. (4) and the crosses from the stochastic model, Eqs. (7) – (10), with m0 = 0. (B). 50% penetration time as function of the selection coefficient when the initial presence of mutants is determined by mutation-selection balance, m0 = Nf0 = uN/|s0|. Results are for s0 = −0.02, N = 107 and, from top to bottom, u = 10−6, 10−7, 10−8. The red lines are from Eq. (6), and the crosses are from the stochastic model, Eqs. (7) – (10). Discussion
Antibiotic concentrations in natural environments can vary extensively depending on the particular environment. For example, in connection with polluting pharmaceutical industries or at sewage outlets from hospitals the concentrations can reach very high levels (mg/ml), with fluoroquinolones frequently reaching the highest levels [19], [20], [21] whereas in aquatic environments or in soil levels are typically much lower [8]. The presented data suggests that even in those environments with very low antibiotic concentrations, maintenance and selection of resistant bacteria can occur. For example, the MSC for ciprofloxacin and tetracycline obtained from our experiments correspond to 100 pg/ml and 15 ng/ml, respectively, similar to concentrations that can be found in some aquatic and soil environments [8]. Thus, the surprisingly high frequencies of antibiotic-resistant bacteria found in animals from relatively pristine environments [22], [23], [24] could conceivably be partly explained by enrichment due to sub-MIC selective effects.
These findings are also highly relevant with regard to the question of reversibility of resistance. Since most antibiotic resistance mechanisms are associated with a fitness cost it has been proposed that the fitness costs of resistance will allow susceptible bacteria to out-compete resistant bacteria if the antibiotic selective pressure is reduced. However, most available data suggests that the rate of reversibility will be slow or absent at the community level [25]. Several factors could contribute to this irreversibility, including the absence of a fitness cost, reduction of the fitness cost through compensating mutations and genetic co-selection between the resistance-conferring gene and another gene under selection. In addition, the sub-MIC selection observed here could be a significant contributor to this long-term persistence of resistance where very low antibiotic concentrations in the environment are sufficient to maintain the existing resistant bacteria in the population by further balancing the fitness cost of the resistance. This can be particularly important for bacterial pathogens whose normal life cycle involves growth in soil environments (e.g. P. aeruginosa) or periodic growth in aquatic environments (e.g. E. coli).
From the slope of the graphs in Fig. 2B, D and Fig. 3B, D, F and H we can infer that the fitness cost of the resistance mutation has a major influence on the value of the MSC. This cost must first be overcome by a negative effect of antibiotics on the susceptible bacteria before resistant bacteria will be selected, shifting the MSC towards higher concentrations. Reducing this cost will shift the curve upwards and lower the MSC. It is also evident that the increased resistance of the mutants (difference between MICsusc. and MICres.) or the mode of resistance (point mutation or efflux pumps) has little effect on MSC relative to the fitness cost. Since our data was obtained in defined genetic backgrounds with single point mutations or deletions commonly found for the antibiotics tested, the fitness cost represents the cost of a de novo resistance mutation. However, in most resistant strains found clinically the fitness cost of resistance is frequently compensated for by secondary mutations without a loss of resistance [25]. Such fitness compensation has been described for resistance to many different antibiotics including fluoroquinolones and streptomycin [26], [27], [28]. This implies that the antibiotic concentrations at which such compensated resistant strains will be selected can be even lower than what we have measured here.
Another significant implication from our and the findings of others is that the widely used concept of the mutant selective window needs modification. Thus, in pharmacodynamics it is generally assumed that antibiotic concentrations below the MIC do not confer selection and that the mutant selective window—the concentration range in which the resistant mutant is enriched—extends between the MIC of the susceptible wild type and the MIC of the resistant mutants [11], [12]. However, our results imply that the biologically relevant sub-MIC selective window is much wider and needs to include antibiotic concentrations several hundred-fold below MICsusc (Fig. 1A). Furthermore, the methodology described here could be used to probe the biologically active antibiotic concentrations in different environments, including for example animal models. Thus, by performing competitions between genetically tagged susceptible and resistant strains in animals treated with different antibiotic concentrations one can from the enrichment rate of resistant bacteria infer the biologically active concentration of antibiotic at the site of bacterial growth.
At selection above the MIC of a strain, the main driving force of the selection is antibiotic resistance, while the fitness cost of the mutation is less critical. Even mutations with a very high cost will be selected, since competitors in the form of susceptible bacteria will be eliminated. At sub-MIC levels, however, the situation is different since the susceptible bacteria will not die, they will only grow slower. Because of this, resistance mutations conferring high fitness costs will not be enriched; only mutations where the fitness cost is lower than the growth reduction caused by the antibiotic in the susceptible bacteria will be competitive. This suggests that a new spectrum of low-cost or no-cost resistance mutations might be enriched during such conditions. The data in Fig. 5, show that these sub-MIC levels of antibiotics do not only enrich for pre-existing resistant mutants, but they can also select for resistant mutants de novo from a susceptible population. It is interesting to note that despite the low antibiotic concentrations used, mutants with high resistance levels were enriched. Since the streptomycin concentration chosen for the de novo mutant selection experiment is the same as the MSC determined in the competitions between wild type and an rpsL K42R mutant, the enriched resistant bacteria are likely to carry resistance mutations with a fitness cost that is significantly lower than the previously studied rpsL mutation.
In the presented experiments pre-existing mutants were rapidly enriched in competitions with susceptible strains. From the mathematical model we can infer a similar situation for de novo resistant mutants, especially in large populations where uN >1 and at antibiotic concentrations where 0.01< s <1.0. In those situations resistant mutants rapidly appear and within 100–1000 generations of growth they will take over the population. The model is supported by the experiments shown in Fig. 5 and Fig. S2, where de novo mutants continuously increased in frequency during 600–700 generations of growth in the presence of sub-MIC levels of antibiotics.
In conclusion, the presented data suggests that the very low antibiotic levels which are present in many natural environments or generated in certain body compartments during treatment are relevant for the enrichment and maintenance of pre-existing resistant mutants as well as for the de novo selection of new mutants. These results emphasize the importance of introducing measures that reduce antibiotic levels in the environment and use of treatment dosing regimens that preclude prolonged time periods of sub-MIC levels of antibiotics.
Materials and Methods
Bacterial strains, genetic methods, and growth conditions
Strains used in this study were derived from Escherichia coli MG1655 and Salmonella enterica serovar Typhimurium LT2 (designated S. typhimurium in the text) and are listed in Table S1 in Text S1. The resistant strains were constructed by P22 transduction (S typhimurium) or P1 transduction (E coli) of the resistance genes into the parental strains. The liquid and solid media used for bacterial growth were Mueller–Hinton broth (Becton Dickinson, MD, USA), Mueller–Hinton agar (Mueller–Hinton broth supplemented with 1.5% agar) and Luria–Bertani (LB) agar (Sigma-Aldrich, MO, USA). Strains were grown at 37°C, and liquid cultures were aerated by shaking.
Growth rate measurements
Growth rates were measured at 37°C in Mueller-Hinton broth, with or without tetracycline present, using a Bioscreen C Analyzer (Oy Growth Curves Ab Ltd, Helsinki, Finland). Each well was inoculated with a 1000-fold dilution of an overnight culture and measurements at each antibiotic concentration were made in quadruplicate. The cultures were grown for 24 hours with continuous shaking, and OD600 measurements were taken every 4 min. The calculations were based on OD600 values between 0.02 and 0.1, where growth was observed to be exponential. The sensitive strain (DA6192) and the resistant strain (DA17822) were grown in separate experiments, and the relative growth rates were calculated as the derived growth rates divided by the growth rate of the same strain grown without antibiotics.
MIC measurements
MIC assays of tetracycline and ciprofloxacin were performed by broth macrodilution in 10 mL tubes. Tubes containing Mueller-Hinton broth (1 mL) supplemented with different concentrations of antibiotics were inoculated with 1 µL of an overnight bacterial culture grown at 37°C. The tubes were incubated at 37°C with shaking for 16 to 18 hours, the tetracycline cultures protected from light to avoid degradation of the antibiotic. The MIC was set to the lowest concentration of antibiotic yielding no visible growth. The MIC of streptomycin was determined by Etest according to the instructions of the manufacturer (AB bioMerieux, Solna, Sweden). Etests were performed on Mueller-Hinton agar plates incubated for 16–18 h at 37°C.
Competition experiments
Limited sampling of competitors (<103 cells) commonly introduces statistical uncertainties in competition experiments and more accurate measurements of resistant mutant to wild type cell ratios can be obtained with the aid of chromosomal copies of either the cyan (cfp) or yellow (yfp) variants of green fluorescent protein gene (gfp). These allow tracking of large numbers of single cells (105 cells) using a fluorescence activated cell sorter (FACS). The cfp/yfp genes were inserted into galK using the λ Red system as previously described [29] and moved by phage P22 transduction or phage P1 transduction into the various strains.
Overnight cultures grown in Mueller-Hinton medium of the susceptible wild type strains with either cfp or yfp, were mixed 1∶1, 10∶1, 102∶1, 103∶1 and 104∶1 with the isogenic resistant mutant carrying the other marker and maintained by 1000-fold serial dilution (resulting in 10 generations of growth per serial passage) every 24 hours for up to 4 to 6 serial passages. The ratio of resistant to susceptible cells in the population was determined at each serial passage by counting 105 cells using a fluorescence-activated cell sorter (BD FacsAria). The selection coefficients were determined using the regression model s = [ln(R(t)/R(0))]/[t], as previously described [30] where R is the ratio of resistant to susceptible. This protocol allowed reproducible determinations of fitness differences as small as s = 0.003 [17]. Two independently constructed sets of each wild type strain, marked with either cfp or yfp, were also included to measure the relative impact on growth rates of having a cfp marker compared to yfp. These control experiments showed that over 40 generations of competition, the difference in cost between the markers had a negligible impact on growth rates. (Fig. S1). The competition experiments performed with a low initial fraction of resistant mutants were done with tetracycline due to the long time required for the appearance of de novo tetracycline resistant mutants that might disturb the competition experiments.
Enrichment of de novo evolved resistant mutants
To investigate whether sub-inhibitory antibiotic concentration could also select for de novo generated resistant mutants, susceptible bacteria was serially passaged at 1/4 of the MIC of streptomycin and at 1/10 of the MIC of ciprofloxacin. A total of 20 independent lineages of S. typhimurium LT2 was serially passaged by 1000-fold dilution in 1 ml batch cultures every 24 hours for 700 generations (10 generations of growth per serial passage) in Mueller-Hinton medium containing 1 µg/ml streptomycin, and 20 independent lineages of E. coli MG1655 were serially passaged by 1000-fold dilution in 1 ml batch cultures every 24 hours for 600 generations in Mueller-Hinton medium containing 2.3 ng/ml ciprofloxacin. The lineages were started from overnight cultures from independent colonies, using an initial bottleneck of approximately 104 cells to minimize the number of preexisting resistant mutants. The percentage of resistant cells in each culture was monitored by plating approximately 105 cells onto LB agar containing different concentrations of antibiotics every 100 generations and counting the number of colonies. A subset of these cells were restreaked on the same antibiotic concentration to confirm that they were resistant.
Accession numbers
Tn10 (Transposon Tn10 tetracycline resistance and repressor genes tetA and tetR)
GenBank: J01830.1
rpsL (30S ribosomal protein S12)
GenBank: AAL22311.1
Swiss-Prot: P0A7S6
gyrA (DNA gyrase subunit A)
GenBank: AAC75291.1
Swiss-Prot: P0AES4
acrR (HTH-type transcriptional regulator AcrR)
GenBank: AAC73566.1
Swiss-Prot: P0ACS9
marR (Multiple antibiotic resistance protein MarR)
GenBank: AAC74603.2
Swiss-Prot: P27245
gfp (Green fluorescent protein)
GenBank: AAA27722.1
Swiss-Prot: P42212
Supporting Information
Zdroje
1. RiceLB 2009 The clinical consequences of antimicrobial resistance. Curr Opin Microbiol 12 476 481
2. WitteW 1998 Medical consequences of antibiotic use in agriculture. Science 279 996 997
3. AarestrupFM 2005 Veterinary drug usage and antimicrobial resistance in bacteria of animal origin. Basic Clin Pharmacol 96 271 281
4. MartinezJL 2008 Antibiotics and antibiotic resistance genes in natural environments. Science 321 365 367
5. FerberD 2000 Superbugs on the hoof? Science 288 792 794
6. McManusPSStockwellVOSundinGWJonesAL 2002 Antibiotic use in plant agriculture. Annu Rev Phytopathol 40 443 465
7. CabelloFC 2006 Heavy use of prophylactic antibiotics in aquaculture: a growing problem for human and animal health and for the environment. Environ Microbiol 8 1137 1144
8. KummererK 2009 Antibiotics in the aquatic environment - A review - Part I. Chemosphere 75 417 434
9. Thiele-BruhnS 2003 Pharmaceutical antibiotic compounds in soils - a review. J Plant Nutr Soil Sc 166 145 167
10. ChanderYKumarKGoyalSMGuptaSC 2005 Antibacterial activity of soil-bound antibiotics. J Environ Qual 34 1952 1957
11. DrlicaK 2003 The mutant selection window and antimicrobial resistance. J Antimicrob Chemoth 52 11 17
12. DrlicaKZhaoXL 2007 Mutant selection window hypothesis updated. Clin Infect Dis 44 681 688
13. NegriMCLipsitchMBlazquezJLevinBRBaqueroF 2000 Concentration-dependent selection of small phenotypic differences in TEM beta-lactamase-mediated antibiotic resistance. Antimicrob Agents Ch 44 2485 2491
14. BaqueroFNegriMCMorosiniMIBlazquezJ 1998 Antibiotic-selective environments. Clin Infect Dis 27 S5 S11
15. BaqueroFNegriMCMorosiniMIBlazquezJ 1998 Selection of very small differences in bacterial evolution. Int Microbiol 1 295 300
16. LiuAFongABecketEYuanJTamaeC 2011 Selective advantage of resistant strains at trace levels of antibiotics: a simple and ultrasensitive color test for detection of antibiotics and genotoxic agents. Antimicrob Agents Chemother 55 1204 1210
17. LindPATobinCBergOGKurlandCGAnderssonDI 2010 Compensatory gene amplification restores fitness after inter-species gene replacements. Mol Microbiol 75 1078 1089
18. KohanskiMADePristoMACollinsJJ 2010 Sublethal Antibiotic Treatment Leads to Multidrug Resistance via Radical-Induced Mutagenesis. Mol Cell 37 311 320
19. LarssonDGJde PedroCPaxeusN 2007 Effluent from drug manufactures contains extremely high levels of pharmaceuticals. J Hazard Mater 148 751 755
20. LiDYangMHuJRenLZhangY 2008 Determination and fate of oxytetracycline and related compounds in oxytetracycline production wastewater and the receiving river. Environ Toxicol Chem 27 80 86
21. LiDYangMHuJYZhangYChangH 2008 Determination of penicillin G and its degradation products in a penicillin production wastewater treatment plant and the receiving river. Water Res 42 307 317
22. SjolundMBonnedahlJHernandezJBengtssonSCederbrantG 2008 Dissemination of multildrug-resistant bacteria into the Arctic. Emerg Infect Dis 14 70 72
23. OsterbladMNorrdahlKKorpimakiEHuovinenP 2001 Antibiotic resistance - How wild are wild mammals? Nature 409 37 38
24. GilliverMABennettMBegonMHazelSMHartCA 1999 Enterobacteria - Antibiotic resistance found in wild rodents. Nature 401 233 234
25. AnderssonDIHughesD 2010 Antibiotic resistance and its cost: is it possible to reverse resistance? Nat Rev Microbiol 8 260 271
26. BjorkmanJNagaevIBergOGHughesDAnderssonDI 2000 Effects of environment on compensatory mutations to ameliorate costs of antibiotic resistance. Science 287 1479 1482
27. BjorkmanJHughesDAnderssonDI 1998 Virulence of antibiotic-resistant Salmonella typhimurium. Proc Natl Acad Sci USA 95 3949 3953
28. MarcussonLLFrimodt-MollerNHughesD 2009 Interplay in the Selection of Fluoroquinolone Resistance and Bacterial Fitness. Plos Pathog 5 e1000541
29. ElowitzMBLevineAJSiggiaEDSwainPS 2002 Stochastic gene expression in a single cell. Science 297 1183 1186
30. DykhuizenDE 1990 Experimental Studies of Natural-Selection in Bacteria. Annu Rev Ecol Syst 21 373 398
Štítky
Hygiena a epidemiologie Infekční lékařství Laboratoř
Článek A Typhimurium-Typhi Genomic Chimera: A Model to Study Vi Polysaccharide Capsule Function In VivoČlánek SUMO Pathway Dependent Recruitment of Cellular Repressors to Herpes Simplex Virus Type 1 GenomesČlánek A Structural Model for Binding of the Serine-Rich Repeat Adhesin GspB to Host Carbohydrate ReceptorsČlánek Dynamic Evolution of Pathogenicity Revealed by Sequencing and Comparative Genomics of 19 IsolatesČlánek Widespread Endogenization of Genome Sequences of Non-Retroviral RNA Viruses into Plant GenomesČlánek The Cost of Virulence: Retarded Growth of Typhimurium Cells Expressing Type III Secretion System 1Článek A Role for the Chemokine RANTES in Regulating CD8 T Cell Responses during Chronic Viral Infection
Článek vyšel v časopisePLOS Pathogens
Nejčtenější tento týden
2011 Číslo 7- Jak souvisí postcovidový syndrom s poškozením mozku?
- Stillova choroba: vzácné a závažné systémové onemocnění
- Diagnostika virových hepatitid v kostce – zorientujte se (nejen) v sérologii
- Perorální antivirotika jako vysoce efektivní nástroj prevence hospitalizací kvůli COVID-19 − otázky a odpovědi pro praxi
- Diagnostický algoritmus při podezření na syndrom periodické horečky
-
Všechny články tohoto čísla
- What Do We Really Know about How CD4 T Cells Control ?
- “Persisters”: Survival at the Cellular Level
- E6 and E7 from Beta Hpv38 Cooperate with Ultraviolet Light in the Development of Actinic Keratosis-Like Lesions and Squamous Cell Carcinoma in Mice
- Selection of Resistant Bacteria at Very Low Antibiotic Concentrations
- The Extracytoplasmic Domain of the Ser/Thr Kinase PknB Binds Specific Muropeptides and Is Required for PknB Localization
- CD39/Adenosine Pathway Is Involved in AIDS Progression
- Hypoxia and a Fungal Alcohol Dehydrogenase Influence the Pathogenesis of Invasive Pulmonary Aspergillosis
- One Is Enough: Effective Population Size Is Dose-Dependent for a Plant RNA Virus
- Effects of Interferon-α/β on HBV Replication Determined by Viral Load
- A Typhimurium-Typhi Genomic Chimera: A Model to Study Vi Polysaccharide Capsule Function In Vivo
- Dual Chaperone Role of the C-Terminal Propeptide in Folding and Oligomerization of the Pore-Forming Toxin Aerolysin
- Rotavirus Stimulates Release of Serotonin (5-HT) from Human Enterochromaffin Cells and Activates Brain Structures Involved in Nausea and Vomiting
- Dissociation of Infectivity from Seeding Ability in Prions with Alternate Docking Mechanism
- The Impact of Recombination on dN/dS within Recently Emerged Bacterial Clones
- The Regulation of Sulfur Metabolism in
- Illumination of Parainfluenza Virus Infection and Transmission in Living Animals Reveals a Tissue-Specific Dichotomy
- A Permeable Cuticle Is Associated with the Release of Reactive Oxygen Species and Induction of Innate Immunity
- A Concerted Action of Hepatitis C Virus P7 and Nonstructural Protein 2 Regulates Core Localization at the Endoplasmic Reticulum and Virus Assembly
- SUMO Pathway Dependent Recruitment of Cellular Repressors to Herpes Simplex Virus Type 1 Genomes
- Re-localization of Cellular Protein SRp20 during Poliovirus Infection: Bridging a Viral IRES to the Host Cell Translation Apparatus
- Divergent Effects of Human Cytomegalovirus and Herpes Simplex Virus-1 on Cellular Metabolism
- A Structural Model for Binding of the Serine-Rich Repeat Adhesin GspB to Host Carbohydrate Receptors
- Transformation of Natural Genetic Variation into Genomes
- EBV Latency Types Adopt Alternative Chromatin Conformations
- Global mRNA Degradation during Lytic Gammaherpesvirus Infection Contributes to Establishment of Viral Latency
- Dynamic Evolution of Pathogenicity Revealed by Sequencing and Comparative Genomics of 19 Isolates
- Microbial Virulence as an Emergent Property: Consequences and Opportunities
- Widespread Endogenization of Genome Sequences of Non-Retroviral RNA Viruses into Plant Genomes
- Structural Basis of Chemokine Sequestration by CrmD, a Poxvirus-Encoded Tumor Necrosis Factor Receptor
- Cross-Species Transmission of a Novel Adenovirus Associated with a Fulminant Pneumonia Outbreak in a New World Monkey Colony
- An Interaction between KSHV ORF57 and UIF Provides mRNA-Adaptor Redundancy in Herpesvirus Intronless mRNA Export
- Elevated 17β-Estradiol Protects Females from Influenza A Virus Pathogenesis by Suppressing Inflammatory Responses
- The Role of IL-15 Deficiency in the Pathogenesis of Virus-Induced Asthma Exacerbations
- Fluorescence Lifetime Imaging Unravels Metabolism and Its Crosstalk with the Host Cell
- Programmed Death (PD)-1-Deficient Mice Are Extremely Sensitive to Murine Hepatitis Virus Strain-3 (MHV-3) Infection
- Hemoglobin Promotes Nasal Colonization
- Crystallography of a Lewis-Binding Norovirus, Elucidation of Strain-Specificity to the Polymorphic Human Histo-Blood Group Antigens
- The Cost of Virulence: Retarded Growth of Typhimurium Cells Expressing Type III Secretion System 1
- A Genome-Wide Approach to Discovery of Small RNAs Involved in Regulation of Virulence in
- Requires Glycerol for Maximum Fitness During The Tick Phase of the Enzootic Cycle
- C Metabolic Flux Analysis Identifies an Unusual Route for Pyruvate Dissimilation in Mycobacteria which Requires Isocitrate Lyase and Carbon Dioxide Fixation
- A Role for the Chemokine RANTES in Regulating CD8 T Cell Responses during Chronic Viral Infection
- Glycosaminoglycans and Sialylated Glycans Sequentially Facilitate Merkel Cell Polyomavirus Infectious Entry
- Regulation of Stomatal Tropism and Infection by Light in : Evidence for Coordinated Host/Pathogen Responses to Photoperiod?
- Multiple Translocation of the Effector Gene among Chromosomes of the Rice Blast Fungus and Related Species
- Comparative Genomics Yields Insights into Niche Adaptation of Plant Vascular Wilt Pathogens
- Unique Cell Adhesion and Invasion Properties of O:3, the Most Frequent Cause of Human Yersiniosis
- C-Terminal Region of EBNA-2 Determines the Superior Transforming Ability of Type 1 Epstein-Barr Virus by Enhanced Gene Regulation of LMP-1 and CXCR7
- Novel Chikungunya Vaccine Candidate with an IRES-Based Attenuation and Host Range Alteration Mechanism
- PLOS Pathogens
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Requires Glycerol for Maximum Fitness During The Tick Phase of the Enzootic Cycle
- Comparative Genomics Yields Insights into Niche Adaptation of Plant Vascular Wilt Pathogens
- The Role of IL-15 Deficiency in the Pathogenesis of Virus-Induced Asthma Exacerbations
- “Persisters”: Survival at the Cellular Level
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání



