-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaDynamics of Transcription Factor Binding Site Evolution
Evolution has produced a remarkable diversity of living forms that manifests in qualitative differences as well as quantitative traits. An essential factor that underlies this variability is transcription factor binding sites, short pieces of DNA that control gene expression levels. Nevertheless, we lack a thorough theoretical understanding of the evolutionary times required for the appearance and disappearance of these sites. By combining a biophysically realistic model for how cells read out information in transcription factor binding sites with model for DNA sequence evolution, we explore these timescales and ask what factors crucially affect them. We find that the emergence of binding sites from a random sequence is generically slow under point and insertion/deletion mutational mechanisms. Strong selection, sufficient genomic sequence in which the sites can evolve, the existence of partially decayed old binding sites in the sequence, as well as certain biophysical mechanisms such as cooperativity, can accelerate the binding site gain times and make them consistent with the timescales suggested by comparative analyses of genomic data.
Published in the journal: . PLoS Genet 11(11): e32767. doi:10.1371/journal.pgen.1005639
Category: Research Article
doi: https://doi.org/10.1371/journal.pgen.1005639Summary
Evolution has produced a remarkable diversity of living forms that manifests in qualitative differences as well as quantitative traits. An essential factor that underlies this variability is transcription factor binding sites, short pieces of DNA that control gene expression levels. Nevertheless, we lack a thorough theoretical understanding of the evolutionary times required for the appearance and disappearance of these sites. By combining a biophysically realistic model for how cells read out information in transcription factor binding sites with model for DNA sequence evolution, we explore these timescales and ask what factors crucially affect them. We find that the emergence of binding sites from a random sequence is generically slow under point and insertion/deletion mutational mechanisms. Strong selection, sufficient genomic sequence in which the sites can evolve, the existence of partially decayed old binding sites in the sequence, as well as certain biophysical mechanisms such as cooperativity, can accelerate the binding site gain times and make them consistent with the timescales suggested by comparative analyses of genomic data.
Introduction
Evolution produces heritable phenotypic variation within and between populations and species on relatively short timescales. Part of this variation is due to differences in gene regulation, which determines how much of each gene product exists in every cell. These gene expression levels are heritable quantitative traits subject to natural selection [1–3]. While the importance of their variability for the observed phenotypic variation is still debated [4], it is believed to be crucial within closely related species or in populations whose proteins are functionally or structurally similar [5]. The genetic basis for gene expression differences is thought to be non-coding regulatory DNA, but our understanding of its evolution is still immature; this is due, in part, to the lack of precise knowledge about the mapping between the regulatory sequence and the resulting expression levels.
Transcriptional regulation is the most extensively studied mechanism of gene regulation. Transcription factor proteins (TFs) recognize and bind specific DNA sequences called binding sites, thereby affecting the expression of target genes. Eukaryotic regulatory sequences, i.e., enhancers and promoters, are typically between a hundred and several thousand base pairs (bp) in length [6], and can harbor many transcription factor binding sites (TFBSs), each typically consisting of 6–12 bp. The situation is different in prokaryotes: they lack enhancer regions and have one or a few TFBSs which are typically longer, between 10 to 20 bp in length [7, 8]. Differences in TF binding are thought to arise primarily due to changes in the regulatory sequence at the TF binding sites rather than changes in the cellular environment or the TF proteins themselves [10]. Nevertheless, a theoretical understanding of the relationship between the evolution of the regulatory sequence and the evolution of gene expression levels remains elusive, mostly because of the complex interaction of evolutionary forces and biophysical processes [11].
From the evolutionary perspective, the crucial question is whether and when these regulatory sequences can evolve rapidly enough so that new phenotypic variants can arise and fix in the population over typical speciation timescales. Comparative genomic studies in eukaryotes provide evidence for the evolutionary dynamics of TF binding, highlighting the possibility for rapid and flexible TFBS gain and loss between closely related species on timescales of as little as a few million years [12, 13]. Examples include quick gain and loss events that cause divergent gene expression [14], or the compensation of such events by turn-over at other genome locations [15]; gain and loss events sometimes occur even in the presence of strong constraints on expression levels [16, 17]. Furthermore, such events enabled new binding sites on sex chromosomes that arose as recently as 1–2 million years ago [18, 19]. There are examples of rapid regulatory DNA evolution across and within populations requiring shorter timescales, i.e. 10.000–100.000 years [2, 20–22]. On the other hand, strict conservation has also been observed at orthologous regulatory locations even in distant species (e.g., [23]). Taken together, these facts suggest that the rates of TFBS evolution can extend over many orders of magnitude and differ greatly from the point mutation rate at a neutral site. To study the evolutionary dynamics of regulatory sequences and understand the relevant timescales, we set up a theoretical framework with a special focus on the interplay of both population genetic and biophysical factors, briefly outlined below.
Sequence innovations originate from diverse mutational mechanisms in the genome. While tandem repeats [24] or transposable elements [25] may be important in evolution, the better studied and more widespread mutation types still need to be better understood in the context of TFBS evolution. Specifically, we ask how the evolutionary dynamics are affected by single nucleotide (point) mutations, as well as by insertions and deletions (indels). New mutations in the population are selected or eliminated by the combined effects of selection and random genetic drift. Although the importance of selection [26–28] and mutational closeness of the initial sequences [29, 30] for TF binding site evolution has already been reported, the belief in fast evolution via point mutations without selection (i.e., neutral evolution) persists in the literature (e.g., [5, 13]), mainly due to Stone & Wray’s (2001) misinterpretation of their own simulation results [31] (see Macarthur & Brookfield (2004) [29]). This likely reflects the current lack of theoretical understanding of TFBS evolution in the literature, even under the simplest case of directional selection. Basic population genetics shows that directional selection is expected to cause a change, e.g., yield a functional binding site, over times on the order of 1/(NsUb), where N is the population size, s is the selection advantage of a binding site, and Ub is the beneficial mutation rate [32]. This process can be extremely slow, especially under neutrality, if several mutational steps are needed to reach a sequence with sufficient binding energy to confer a selective advantage. As already pointed out by Berg et al. (2004) [32], this places strong constraints on the length of the binding sites, if they were to evolve from random sequences.
Several biophysical factors, such as TF concentration and the energetics of TF-DNA and TF-TF interactions, might play an important role in TFBS evolution. Quantitative models for TF sequence specificity [33–38] and for thermodynamic (TD) equilibrium of TF occupancy on DNA [34, 39–43] were developed in recent decades and, in parallel with developments in sequencing, have contributed to our understanding of TF-DNA interaction biophysics. These biophysical factors can shape the characteristics of the TFBS fitness landscape over genotype space in evolutionary models [8, 29, 32, 44–47]. There are also intensive efforts to understand the mapping from promoter/enhancer sequences to gene expression [42, 48–50]. Despite this recent attention, there have been relatively few attempts to understand the evolutionary dynamics of TFBS in full promoter/enhancer regions [29, 43, 51–53], especially using biophysically realistic but still mathematically tractable models. Such models are necessary to gain a thorough theoretical understanding of binding site evolution.
Our aim in this study is to investigate the dynamics of TFBS evolution by focusing on the typical evolutionary rates for individual TFBS gain and loss events. We consider both a single binding site at an isolated DNA region and a full enhancer/promoter region, able to harbor multiple binding sites. In the following section, we lay out our modeling framework, which covers both population genetic and biophysical considerations, as outlined above. Using this framework, we try to understand i) what typical gain and loss rates are for a single TFBS site; ii) how quickly populations converge to a stationary distribution for a single TFBS; iii) how multiple TFBS evolve in enhancers and promoters; iv) how early history of the evolving sequences can change the evolutionary rates of TFBS; and v) how cooperativity between TFs affects the evolution of gene expression. We find that, under realistic parameter ranges, both gain and loss of a single binding site is slow, slower than the typical divergence time between species. Importantly, fast emergence of an isolated TFBS requires strong selection and favorable initial sequences in the mutational neighborhood of a strong TFBS. The evolutionary process approaches the equilibrium distribution very slowly, raising concerns about the use of equilibrium assumptions in theoretical work. We proceed to show that the dynamics of TFBS evolution in larger sequences can be understood approximately from the dynamics of single binding sites; the TFBS gain times are again slow if evolution starts from random sequence in the absence of strong selection or large regulatory sequence “real estate.” Finally, we identify two factors that can speed up the emergence of TFBS: the existence of an initial sequence distribution biased towards the mutational neighborhood of strongly binding sequences, which suggests that ancient evolutionary history can play a major role in the emergence of “novelties” [54]; and the biophysical cooperativity between transcription factors, which can partially account for the lack of observed correlation between identifiable binding sequences and transcriptional activity [11].
Methods
Population genetics
We consider a finite population of N diploid individuals whose genetic content consists of an evolvable L base pair (bp) contiguous regulatory sequence σ to which TFs can bind. Given that σi ∈ {A, C, G, T} where i = 1, 2, …, L indexes the position in regulatory sequence, there are 4L different regulatory sequences in the genotype space. Each TF is assumed to bind to a contiguous sequence of n bp within our focal region of L bp (Fig 1A and 1B). Regulatory sequences evolve under mutation, selection, and sampling drift. The rest of the genome is assumed to be identical for all individuals and is kept constant. In the first part of our study we consider the regulatory sequence comprised of a single TFBS (i.e. L = n). Later, we consider the evolution of a longer sequence (i.e. L ≫ n) in which more than one TFBS can evolve. For simulations, we use a Wright-Fisher model where N diploid individuals are sampled from the previous generation after mutation and selection. Our analytical treatment is general and corresponds to setups where a diffusion approximation to allele frequency evolution is valid. We neglect recombination since typical regulatory sequences are short, L ≤ 1000. To be consistent with most of the population genetics literature we assume diploidy, but since we do not consider any dominance effects, our results also hold for a haploid population with 2N individuals.
Fig. 1. Biophysics of transcription regulation. 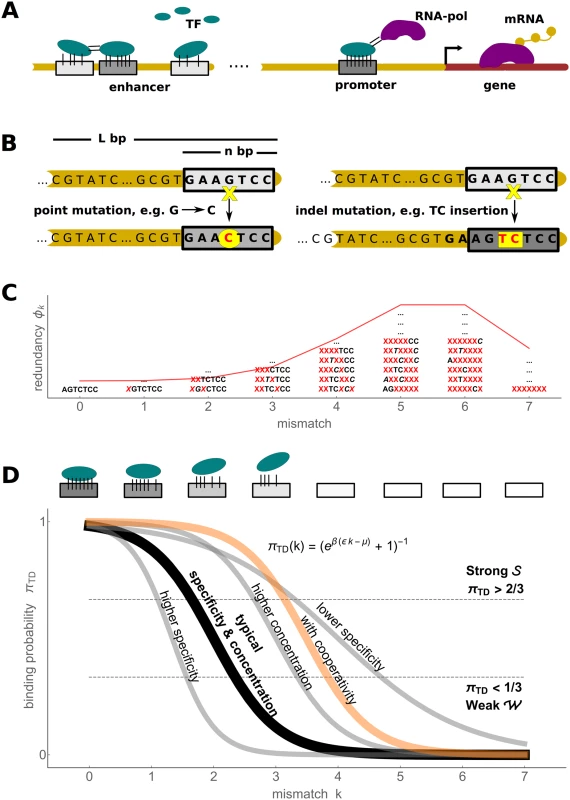
A) TFs bind to regulatory DNA regions (promoters and enhancers) in a sequence-specific manner to regulate transcriptional gene expression (mRNA production) level via different mechanisms, such as recruiting RNA polymerase (RNA-pol). B) A schematic of two types of mutational processes that we model: point mutations (left) and indel mutations (right). C) The mismatch binding model results in redundancy of genotype classes, with a binomial distribution (red) of genotypes in each mismatch class (some examples of degenerate sequences shown) D) The mapping from the TFBS regulatory sequence to gene expression level is determined by the thermodynamic occupancy (binding probability) of the binding site. If each of the k mismatches from the consensus sequence decreases the binding energy by ϵ, the occupancy of the binding site is πTD(k) = (1 + eβ(ϵk−μ))−1, where μ is the chemical potential (related to free TF concentration). A typical occupancy curve is shown in black (ϵ = 2 kB T and μ = 4 kB T); the gray curves show the effect of perturbation to these parameters (ϵ = 1 kB T, ϵ = 3 kB T and μ = 6 kB T); the orange curve illustrates the case of two cooperatively binding TFs (kc = 0 and Ec = −3 kB T, see text for details). We pick two thresholds, shown in dashed lines, to define discrete binding classes: strong Evolutionary dynamics simplify in the low mutation limit where the population consists of a single genotype during most of its evolutionary history (the fixed state population model). Desai & Fisher [55] have shown that the condition log 4 N Δ f Δ f ≪ 1 4 N U b Δ f needs to hold for a fixed state population assumption to be accurate. The term on the left is the establishment time of a mutant allele with a selective advantage Δf relative to the wild type; the term on the right-hand side is the waiting time for such an allele to appear, where Ub is the beneficial mutation rate per individual per generation. Note that, in binding site context, Ub refers to the rate of mutations which increase the fitness, for instance, by increasing binding strength. Its exact value depends on the current state of the genotype; nevertheless, typical value estimates help model the evolutionary dynamics. In multicellular eukaryotes, where most evidence for the evolution of TFBSs has been collected and which provide the motivation for this manuscript, the number of mutations per nucleotide site is typically low, e.g. 4Nu ∼ 0.01 in Drosophila and 4Nu ∼ 0.001 in humans [56], where u is the point mutation rate per generation per base pair. For a single binding site of typical length n ∼ 5–15, one therefore expects the fixed state population model to be accurate. For longer regulatory sequences, one expects that beneficial mutations are rare among all possible mutations, so that the fixed state population model can be assumed to hold as well.
Evolution under the fixed state assumption can be treated as a simple Markovian jump process. The transition rate from a regulatory sequence σ to another regulatory sequence σ′ in a diploid population is
where Δfσ′,σ = f(σ′) − f(σ) is the fitness difference and Uσ′,σ is the mutation rate from σ to σ′. The fixation probability Pfix of a mutation with fitness difference Δf in a diploid population of N individuals is which is based on the diffusion approximation [57]. Note that the fixation probability scaled with 1/N approximates to 2NΔf when NΔf ≫ 1. Evolutionary dynamics therefore depend essentially on how regulatory sequences are mutationally connected in genotype space, and how fitnesses differ between neighboring genotypes, i.e., on the fitness landscape.Directional selection on biophysically motivated fitness landscapes
In this study, we focus on directional selection by assuming that fitness f is proportional to gene expression level g which depends on regulatory sequence, i.e.
where s is the selection strength. It is important to note that this choice does not imply that directional selection is the only natural selection mechanism. It simply aims at obtaining the theoretical upper limits for the rates of gaining and losing binding sites.To analyze a realistic but tractable mapping from the regulatory sequence to fitness, we primarily assume that the proxy for gene expression is the binding occupancy (binding probability) π at a single TF binding site, or the sum of the binding occupancies within an enhancer/promoter region (based on limited experimental support [84]). This corresponds to
where π(i) is the binding occupancy of a site starting at the nucleotide i in sequence σ, and s can be interpreted as the selective advantage of a strongest binding to a weakest binding at a site. We assume all binding sites have equal strength and direction in their contribution towards total gene activation. Sites acting as repressors in our simple model would enter into Eq (4) with a negative selection strength, s. Future studies developing mathematically tractable models should consider more realistic case of unequal contribution with combined activator and repressor sites responding differentially to various regulatory inputs [53]. Although one can postulate different scenarios that map TF occupancies in a long (L ≫ n) promoter to gene expression, we chose the simplest case which allows us to make analytical calculations. Later we relax our assumption on noninteracting binding sites and consider the effects of several kinds of interactions on gene expression and thus on evolutionary dynamics.The occupancy of the TF on its binding site is assumed to be in thermodynamic (TD) equilibrium [34, 39–43]. While this might not always be realistic [58, 59], there is empirical support for this assumption (particularly in prokaryotes) [48, 60, 61], and more importantly, it is sufficient to capture the essential nonlinearity in this genotype-phenotype-fitness mapping [62]. In thermodynamic equilibrium, the binding occupancy at the site starting with the i-th position in regulatory sequence is given by
Here, μ is the chemical potential of the TF (related to its free concentration) [44, 64]; Ei is the sequence specific binding energy, where lower energy corresponds to tighter binding, and β = (kB T)−1. We compute the binding energy Ei by adopting an additive energy model which is considered to be valid at least up to a few mismatches from the consensus sequence [37, 38, 65, 66], i.e. where ξ stands for the energy matrix whose ξσj,j element gives the energetic contribution of the nucleotide σj appearing at the j-th position within TFBS. With this, Eq (4) can be rewritten more formally asTo allow analytical progress, we make the “mismatch assumption,” i.e., the energy matrices contain identical ϵ > 0 entries for every non-consensus (mismatch) base pair; the consensus entries are set to zero by convention. A single binding sequence with k mismatches therefore has the binding energy E = kϵ. We will refer to ϵ as “specificity.” Specificity is provided by diverse interactions between DNA and TF, including specific hydrogen bonds, van der Waals forces, steric exclusions, unpaired polar atoms, etc. [63]. ϵ is expected to be in the range 1–3 kB T, which is consistent with theoretical arguments [44] as well as direct measurements [65–67]. Note that we explicitly check the validity of the analytical results based on the mismatch assumption by comparing them against simulations using realistic energy matrices. The redundancy (i.e., normalized number of distinct sequences) of a mismatch class k at a single site in a random genome can be described by a binomial distribution ϕ (Fig 1C) where the probability of encountering a mismatch class k is
where α = 3/4 in the case of equiprobable distribution over the four nucleotides.We focus on selection in a single environment, which in this framework corresponds to a single choice for the TF concentration. We therefore fix the chemical potential to a baseline value of μ = 4 kB T, which maps changes in the sequence (mismatch class k) to a full range of gene expression levels, as shown in Fig 1D. We subsequently vary μ systematically and report how its value affects the results.
After these preliminaries, the equilibrium binding probability of Eq (5) reduces to
This function has a sigmoid shape whose steepness depends on specificity ϵ and whose midpoint depends on the ratio of chemical potential to specificity, μ/ϵ (Fig 1D). To simplify discussion, we introduce two classes of sequences: genotypes are associated with “strong binding”
Zdroje
1. Fay JC, Wittkopp PJ. Evaluating the role of natural selection in the evolution of gene regulation. Heredity. 2007;100 : 191–199. doi: 10.1038/sj.hdy.6801000 17519966
2. Zheng W, Gianoulis TA, Karczewski KJ, Zhao H, Snyder M. Regulatory Variation Within and Between Species. Annual Review of Genomics and Human Genetics. 2011;12(1):327–346. doi: 10.1146/annurev-genom-082908-150139 21721942
3. Romero IG, Ruvinsky I, Gilad Y. Comparative studies of gene expression and the evolution of gene regulation. Nature Reviews Genetics. 2012 Jul;13(7):505–516. doi: 10.1038/nrg3229 22705669
4. Hoekstra HE, Coyne JA. The locus of evolution: evo devo and the genetics of adaptation. Evolution; International Journal of Organic Evolution. 2007 May;61(5):995–1016. doi: 10.1111/j.1558-5646.2007.00105.x
5. Wittkopp PJ. Evolution of Gene Expression. In: The Princeton Guide to Evolution. Princeton University Press; 2013. p. 413–419.
6. Yao P, Lin P, Gokoolparsadh A, Assareh A, Thang MWC, Voineagu I. Coexpression networks identify brain region-specific enhancer RNAs in the human brain. Nature Neuroscience. 2015 Aug;18(8):1168–1174. doi: 10.1038/nn.4063 26167905
7. Wunderlich Z, Mirny LA. Different gene regulation strategies revealed by analysis of binding motifs. Trends in genetics. 2009 Oct;25(10):434–440. doi: 10.1016/j.tig.2009.08.003 19815308
8. Stewart AJ, Plotkin JB. Why transcription factor binding sites are ten nucleotides long. Genetics. 2012 Nov;192(3):973–985. doi: 10.1534/genetics.112.143370 22887818
9. Lynch M, Hagner K. Evolutionary meandering of intermolecular interactions along the drift barrier. Proceedings of the National Academy of Sciences of the United States of America. 2015. 112:E30–E38. doi: 10.1073/pnas.1421641112 25535374
10. Schmidt D, Wilson MD, Ballester B, Schwalie PC, Brown GD, Marshall A, et al. Five-Vertebrate ChIP-seq Reveals the Evolutionary Dynamics of Transcription Factor Binding. Science. 2010 May;328(5981):1036–1040. doi: 10.1126/science.1186176 20378774
11. Stefflova K, Thybert D, Wilson M, Streeter I, Aleksic J, Karagianni P, et al. Cooperativity and Rapid Evolution of Cobound Transcription Factors in Closely Related Mammals. Cell. 2013 Aug;154(3):530–540. doi: 10.1016/j.cell.2013.07.007 23911320
12. Dowell RD. Transcription factor binding variation in the evolution of gene regulation. Trends in Genetics. 2010 Nov;26(11):468–475. doi: 10.1016/j.tig.2010.08.005 20864205
13. Villar D, Flicek P, Odom DT. Evolution of transcription factor binding in metazoans—mechanisms and functional implications. Nature Reviews Genetics. 2014 Apr;15(4):221–233. doi: 10.1038/nrg3481 24590227
14. Doniger SW, Fay JC. Frequent Gain and Loss of Functional Transcription Factor Binding Sites. PLoS Comput Biol. 2007 May;3(5):e99. doi: 10.1371/journal.pcbi.0030099 17530920
15. Moses AM, Pollard DA, Nix DA, Iyer VN, Li XY, Biggin MD, et al. Large-Scale Turnover of Functional Transcription Factor Binding Sites in Drosophila. PLoS Comput Biol. 2006 Oct;2(10):e130. doi: 10.1371/journal.pcbi.0020130 17040121
16. Ludwig MZ, Patel NH, Kreitman M. Functional analysis of eve stripe 2 enhancer evolution in Drosophila: rules governing conservation and change. Development. 1998;p. 949–958. 9449677
17. Paris M, Kaplan T, Li XY, Villalta JE, Lott SE, Eisen MB. Extensive Divergence of Transcription Factor Binding in Drosophila Embryos with Highly Conserved Gene Expression. PLoS Genet. 2013 Sep;9(9):e1003748. doi: 10.1371/journal.pgen.1003748 24068946
18. Ellison CE, Bachtrog D. Dosage Compensation via Transposable Element Mediated Rewiring of a Regulatory Network. Science. 2013 Nov;342(6160):846–850. doi: 10.1126/science.1239552 24233721
19. Alekseyenko AA, Ellison CE, Gorchakov AA, Zhou Q, Kaiser VB, Toda N, et al. Conservation and de novo acquisition of dosage compensation on newly evolved sex chromosomes in Drosophila. Genes & Development. 2013 Apr;27(8):853–858. doi: 10.1101/gad.215426.113
20. Contente A, Dittmer A, Koch MC, Roth J, Dobbelstein M. A polymorphic microsatellite that mediates induction of PIG3 by p53. Nature Genetics. 2002 Mar;30(3):315–320. doi: 10.1038/ng836 11919562
21. Kasowski M, Grubert F, Heffelfinger C, Hariharan M, Asabere A, Waszak SM, et al. Variation in Transcription Factor Binding Among Humans. Science. 2010 Apr;328(5975):232–235. doi: 10.1126/science.1183621 20299548
22. Chan YF, Marks ME, Jones FC, Villarreal G, Shapiro MD, Brady SD, et al. Adaptive Evolution of Pelvic Reduction in Sticklebacks by Recurrent Deletion of a Pitx1 Enhancer. Science. 2010 Jan;327(5963):302–305. doi: 10.1126/science.1182213 20007865
23. Vierstra J, Rynes E, Sandstrom R, Zhang M, Canfield T, Hansen RS, et al. Mouse regulatory DNA landscapes reveal global principles of cis-regulatory evolution. Science. 2014 Nov;346(6212):1007–1012. doi: 10.1126/science.1246426 25411453
24. Gemayel R, Vinces MD, Legendre M, Verstrepen KJ. Variable Tandem Repeats Accelerate Evolution of Coding and Regulatory Sequences. Annual Review of Genetics. 2010;44(1):445–477. doi: 10.1146/annurev-genet-072610-155046 20809801
25. Feschotte C. Transposable elements and the evolution of regulatory networks. Nature Reviews Genetics. 2008 May;9(5):397–405. doi: 10.1038/nrg2337 18368054
26. Hahn MW, Stajich JE, Wray GA. The Effects of Selection Against Spurious Transcription Factor Binding Sites. Molecular Biology and Evolution. 2003 Jun;20(6):901–906. doi: 10.1093/molbev/msg096 12716998
27. He BZ, Holloway AK, Maerkl SJ, Kreitman M. Does Positive Selection Drive Transcription Factor Binding Site Turnover? A Test with Drosophila Cis-Regulatory Modules. PLoS Genet. 2011 Apr;7(4):e1002053. doi: 10.1371/journal.pgen.1002053 21572512
28. Arnold CD, Gerlach D, Spies D, Matts JA, Sytnikova YA, Pagani M, et al. Quantitative genome-wide enhancer activity maps for five Drosophila species show functional enhancer conservation and turnover during cis-regulatory evolution. Nature Genetics. 2014 Jul;46(7):685–692. doi: 10.1038/ng.3009 24908250
29. MacArthur S, Brookfield JFY. Expected Rates and Modes of Evolution of Enhancer Sequences. Molecular Biology and Evolution. 2004 Jun;21(6):1064–1073. doi: 10.1093/molbev/msh105 15014138
30. Nourmohammad A, Lässig M. Formation of Regulatory Modules by Local Sequence Duplication. PLoS Comput Biol. 2011 Oct;7(10):e1002167. doi: 10.1371/journal.pcbi.1002167 21998564
31. Stone JR, Wray GA. Rapid evolution of cis-regulatory sequences via local point mutations. Molecular Biology and Evolution. 2001 Sep;18(9):1764–1770. doi: 10.1093/oxfordjournals.molbev.a003964 11504856
32. Berg J, Willmann S, Lässig M. Adaptive evolution of transcription factor binding sites. BMC Evolutionary Biology. 2004 Oct;4(1):42. doi: 10.1186/1471-2148-4-42 15511291
33. von Hippel PH, Berg OG. On the specificity of DNA-protein interactions. Proceedings of the National Academy of Sciences of the United States of America. 1986 Mar;83(6):1608–1612. doi: 10.1073/pnas.83.6.1608 3456604
34. Berg OG, von Hippel PH. Selection of DNA binding sites by regulatory proteins. Statistical-mechanical theory and application to operators and promoters. Journal of molecular biology. 1987 Feb;193(4):723–750. doi: 10.1016/0022-2836(87)90354-8 3612791
35. Stormo GD, Fields DS. Specificity, free energy and information content in protein-DNA interactions. Trends in biochemical sciences. 1998 Mar;23(3):109–113. doi: 10.1016/S0968-0004(98)01187-6 9581503
36. Stormo GD, Hartzell GW. Identifying protein-binding sites from unaligned DNA fragments. Proceedings of the National Academy of Sciences. 1989 Feb;86(4):1183–1187. doi: 10.1073/pnas.86.4.1183
37. Stormo GD, Zhao Y. Determining the specificity of protein-DNA interactions. Nature Reviews Genetics. 2010 Nov;11(11):751–760. 20877328
38. Zhao Y, Granas D, Stormo GD. Inferring Binding Energies from Selected Binding Sites. PLoS Comput Biol. 2009 Dec;5(12):e1000590. doi: 10.1371/journal.pcbi.1000590 19997485
39. Shea MA, Ackers GK. The OR Control system of bacteriophage lambda: A physical-chemical model for gene regulation. Journal of Molecular Biology. 1984;p. 211–230.
40. Bintu L, Buchler NE, Garcia HG, Gerland U, Hwa T, Kondev J, et al. Transcriptional regulation by the numbers: applications. Current Opinion in Genetics & Development. 2005;15 : 125–135. doi: 10.1016/j.gde.2005.02.006
41. Bintu L, Buchler NE, Garcia HG, Gerland U, Hwa T, Kondev J, et al. Transcriptional regulation by the numbers: models. Current Opinion in Genetics & Development. 2005;15 : 116–124. doi: 10.1016/j.gde.2005.02.007
42. Hermsen R, Tans S, ten Wolde PR. Transcriptional Regulation by Competing Transcription Factor Modules. PLoS Comput Biol. 2006 Dec;2(12):e164. doi: 10.1371/journal.pcbi.0020164 17140283
43. Hermsen R, Ursem B, ten Wolde PR. Combinatorial Gene Regulation Using Auto-Regulation. PLoS Comput Biol. 2010 Jun;6(6):e1000813. doi: 10.1371/journal.pcbi.1000813 20548950
44. Gerland U, Moroz JD, Hwa T. Physical constraints and functional characteristics of transcription factor-DNA interaction. Proceedings of the National Academy of Sciences of the United States of America. 2002 Sep;99(19):12015–12020. doi: 10.1073/pnas.192693599 12218191
45. Gerland U, Hwa T. On the selection and evolution of regulatory DNA motifs. Journal of Molecular Evolution. 2002 Oct;55(4):386–400. doi: 10.1007/s00239-002-2335-z 12355260
46. Stewart AJ, Plotkin JB. The evolution of complex gene regulation by low-specificity binding sites. Proceedings of the Royal Society B: Biological Sciences. 2013 Oct;280 (1768). doi: 10.1098/rspb.2013.1313
47. Payne JL, Wagner A. The Robustness and Evolvability of Transcription Factor Binding Sites. Science. 2014 Feb;343(6173):875–877. doi: 10.1126/science.1249046 24558158
48. Segal E, Raveh-Sadka T, Schroeder M, Unnerstall U, Gaul U. Predicting expression patterns from regulatory sequence in Drosophila segmentation. Nature. 2008 Jan;451(7178):535–540. doi: 10.1038/nature06496 18172436
49. Samee MAH, Sinha S. Quantitative Modeling of a Gene’s Expression from Its Intergenic Sequence. PLoS Comput Biol. 2014 Mar;10(3):e1003467. doi: 10.1371/journal.pcbi.1003467 24604095
50. He X, Samee AH, Blatti C, Sinha S. Thermodynamics-Based Models of Transcriptional Regulation by Enhancers: The Roles of Synergistic Activation, Cooperative Binding and Short-Range Repression. PLOS Computational Biology. 2010. doi: 10.1371/journal.pcbi.1000935
51. He X, Duque TSPC, Sinha S. Evolutionary Origins of Transcription Factor Binding Site Clusters. Molecular Biology and Evolution. 2012 Mar;29(3):1059–1070. doi: 10.1093/molbev/msr277 22075113
52. Duque T, Samee MAH, Kazemian M, Pham HN, Brodsky MH, Sinha S. Simulations of Enhancer Evolution Provide Mechanistic Insights into Gene Regulation. Molecular Biology and Evolution. 2013 Oct;31(1):184–200. doi: 10.1093/molbev/mst170 24097306
53. Duque T, Sinha S. What Does It Take to Evolve an Enhancer? A Simulation-Based Study of Factors Influencing the Emergence of Combinatorial Regulation. Genome Biology and Evolution. 2015 Jun;7(6):1415–1431. doi: 10.1093/gbe/evv080 25956793
54. Villar D, Berthelot C, Aldridge S, Rayner T, Lukk M, Pignatelli M, et al. Enhancer Evolution across 20 Mammalian Species. Cell. 2015 Jan;160(3):554–566. doi: 10.1016/j.cell.2015.01.006 25635462
55. Desai MM, Fisher DS. Beneficial Mutation-Selection Balance and the Effect of Linkage on Positive Selection. Genetics. 2007 Jul;176(3):1759–1798. doi: 10.1534/genetics.106.067678 17483432
56. Lynch M, Conery JS. The Origins of Genome Complexity. Science. 2003 Nov;302(5649):1401–1404. doi: 10.1126/science.1089370 14631042
57. Kimura M. On the Probability of Fixation of Mutant Genes in a Population. Genetics. 1962 Jun;47(6):713–719. 14456043
58. Hammar P, Wallden M, Fange D, Persson F, Baltekin Ö, Ullman G, et al. Direct measurement of transcription factor dissociation excludes a simple operator occupancy model for gene regulation. Nature Genetics. 2014 Apr;46(4):405–408. doi: 10.1038/ng.2905 24562187
59. Cepeda-Humerez SA, Rieckh G, Tkačik G. Stochastic proofreading mechanism alleviates crosstalk in transcriptional regulation. arXiv:150405716 [q-bio]. 2015 Apr;ArXiv: 1504.05716. Available from: http://arxiv.org/abs/1504.05716
60. Brewster RC, Jones DL, Phillips R. Tuning Promoter Strength through RNA Polymerase Binding Site Design in Escherichia coli. PLoS Computational Biology. 2012 Dec;8(12). doi: 10.1371/journal.pcbi.1002811 23271961
61. Razo-Mejia M, Boedicker JQ, Jones D, DeLuna A, Kinney JB, Phillips R. Comparison of the theoretical and real-world evolutionary potential of a genetic circuit. Physical Biology. 2014 Apr;11(2):026005. doi: 10.1088/1478-3975/11/2/026005 24685590
62. Haldane A, Manhart M, Morozov AV. Biophysical Fitness Landscapes for Transcription Factor Binding Sites. PLoS Comput Biol. 2014 Jul;10(7):e1003683. doi: 10.1371/journal.pcbi.1003683 25010228
63. McKeown AN, Bridgham JT, Anderson DW, Murphy MN, Ortlund EA, Thornton JW. Evolution of DNA Specificity in a Transcription Factor Family Produced a New Gene Regulatory Module. Cell. 2014 Sep;159(1):58–68. doi: 10.1016/j.cell.2014.09.003 25259920
64. Weinert FM, Brewster RC, Rydenfelt M, Phillips R, Kegel WK. Scaling of Gene Expression with Transcription-Factor Fugacity. Physical Review Letters. 2014 Dec;113(25):258101. doi: 10.1103/PhysRevLett.113.258101 25554908
65. Maerkl SJ, Quake SR. A Systems Approach to Measuring the Binding Energy Landscapes of Transcription Factors. Science. 2007 Jan;315(5809):233–237. doi: 10.1126/science.1131007 17218526
66. Kinney JB, Murugan A, Callan CG, Cox EC. Using deep sequencing to characterize the biophysical mechanism of a transcriptional regulatory sequence. Proceedings of the National Academy of Sciences. 2010 May;107(20):9158–9163. doi: 10.1073/pnas.1004290107
67. Fields DS, He Yy, Al-Uzri AY, Stormo GD. Quantitative specificity of the Mnt repressor 1. Journal of Molecular Biology. 1997 Aug;271(2):178–194. doi: 10.1006/jmbi.1997.1171 9268651
68. Mirny LA. Nucleosome-mediated cooperativity between transcription factors. Proceedings of the National Academy of Sciences. 2010 Dec;107(52):22534–22539. doi: 10.1073/pnas.0913805107
69. Taylor MS, Ponting CP, Copley RR. Occurrence and Consequences of Coding Sequence Insertions and Deletions in Mammalian Genomes. Genome Research. 2004 Apr;14(4):555–566. doi: 10.1101/gr.1977804 15059996
70. Brandström M, Ellegren H. The Genomic Landscape of Short Insertion and Deletion Polymorphisms in the Chicken (Gallus gallus) Genome: A High Frequency of Deletions in Tandem Duplicates. Genetics. 2007 Jul;176(3):1691–1701. doi: 10.1534/genetics.107.070805 17507681
71. Park L. Ancestral Alleles in the Human Genome Based on Population Sequencing Data. PLoS ONE. 2015 May;10(5):e0128186. doi: 10.1371/journal.pone.0128186 26020928
72. Cartwright RA. Problems and Solutions for Estimating Indel Rates and Length Distributions. Molecular Biology and Evolution. 2009 Feb;26(2):473–480. doi: 10.1093/molbev/msn275 19042944
73. Chen JQ, Wu Y, Yang H, Bergelson J, Kreitman M, Tian D. Variation in the Ratio of Nucleotide Substitution and Indel Rates across Genomes in Mammals and Bacteria. Molecular Biology and Evolution. 2009 Jul;26(7):1523–1531. doi: 10.1093/molbev/msp063 19329651
74. Lee H, Popodi E, Tang H, Foster PL. Rate and molecular spectrum of spontaneous mutations in the bacterium Escherichia coli as determined by whole-genome sequencing. Proceedings of the National Academy of Sciences. 2012 Oct;109(41):E2774–E2783. doi: 10.1073/pnas.1210309109
75. Keightley PD, Johnson T. MCALIGN: Stochastic Alignment of Noncoding DNA Sequences Based on an Evolutionary Model of Sequence Evolution. Genome Research. 2004 Mar;14(3):442–450. doi: 10.1101/gr.1571904 14993209
76. Wright S. Evolution in Mendelian Populations. Genetics. 1931 Mar;16(2):97–159. 17246615
77. Sella G, Hirsh AE. The application of statistical physics to evolutionary biology. Proceedings of the National Academy of Sciences of the United States of America. 2005;102 : 9541–9546. doi: 10.1073/pnas.0501865102 15980155
78. Mustonen V, Lässig M. Evolutionary population genetics of promoters: Predicting binding sites and functional phylogenies. Proceedings of the National Academy of Sciences of the United States of America. 2005 Nov;102(44):15936–15941. doi: 10.1073/pnas.0505537102 16236723
79. Mustonen V, Kinney J, Callan CG, Lässig M. Energy-dependent fitness: A quantitative model for the evolution of yeast transcription factor binding sites. Proceedings of the National Academy of Sciences of the United States of America. 2008 Aug;105(34):12376–12381. doi: 10.1073/pnas.0805909105 18723669
80. Barton NH, Coe JB. On the application of statistical physics to evolutionary biology. Journal of Theoretical Biology. 2009 Jul;259(2):317–324. doi: 10.1016/j.jtbi.2009.03.019 19348811
81. Manhart M, Haldane A, Morozov AV. A universal scaling law determines time reversibility and steady state of substitutions under selection. Theoretical Population Biology. 2012 Aug;82(1):66–76. doi: 10.1016/j.tpb.2012.03.007 22838027
82. Paixão T, Heredia JP, Sudholt D, Trubenova B. First Steps Towards a Runtime Comparison of Natural and Artificial Evolution. In: Proceedings of the Genetic and Evolutionary Computation Conference, GECCO 2015, Madrid, Spain, July 11–15, 2015. ACM; 2015. p. 1455–1462.
83. Otto SP, Day T. A Biologist’s Guide to Mathematical Modeling in Ecology and Evolution. Princeton University Press; 2007.
84. Giorgetti L, Siggers T, Tiana G, Caprara G, Notarbartolo S, Corona T, et al. Noncooperative Interactions between Transcription Factors and Clustered DNA Binding Sites Enable Graded Transcriptional Responses to Environmental Inputs. Molecular Cell. 2010 Feb;37(3):418–428. doi: 10.1016/j.molcel.2010.01.016 20159560
85. Weirauch MT, Yang A, Albu M, Cote AG, Montenegro-Montero A, Drewe P, et al. Determination and inference of eukaryotic transcription factor sequence specificity. Cell. 2014 Sep;158(6):1431–1443. doi: 10.1016/j.cell.2014.08.009 25215497
86. Rajon E, Masel J. Compensatory Evolution and the Origins of Innovations. Genetics. 2013 Jan;193(4):1209–1220. doi: 10.1534/genetics.112.148627 23335336
Štítky
Genetika Reprodukční medicína
Článek A Hereditary Enteropathy Caused by Mutations in the Gene, Encoding a Prostaglandin TransporterČlánek Exocyst-Dependent Membrane Addition Is Required for Anaphase Cell Elongation and Cytokinesis inČlánek Spindle-F Is the Central Mediator of Ik2 Kinase-Dependent Dendrite Pruning in Sensory Neurons
Článek vyšel v časopisePLOS Genetics
Nejčtenější tento týden
2015 Číslo 11- Srdeční frekvence embrya může být faktorem užitečným v předpovídání výsledku IVF
- Transthyretinová amyloidóza z pohledu neurologa a kardiologa aneb jak se vyhnout „misdiagnostice“?
- Akutní intermitentní porfyrie
- Pánevní endometrióza spojená s volnou tekutinou v peritoneální dutině snižuje úspěšnost otěhotnění po intrauterinní inseminaci
- Primární hyperoxalurie – aktuální možnosti diagnostiky a léčby
-
Všechny články tohoto čísla
- Agricultural Genomics: Commercial Applications Bring Increased Basic Research Power
- Ernst Rüdin’s Unpublished 1922-1925 Study “Inheritance of Manic-Depressive Insanity”: Genetic Research Findings Subordinated to Eugenic Ideology
- Convergent Evolution During Local Adaptation to Patchy Landscapes
- The Locus Controls Age at Maturity in Wild and Domesticated Atlantic Salmon ( L.) Males
- A Hereditary Enteropathy Caused by Mutations in the Gene, Encoding a Prostaglandin Transporter
- Absence of Maternal Methylation in Biparental Hydatidiform Moles from Women with Maternal-Effect Mutations Reveals Widespread Placenta-Specific Imprinting
- Calibrating the Human Mutation Rate via Ancestral Recombination Density in Diploid Genomes
- Anaplastic Lymphoma Kinase Acts in the Mushroom Body to Negatively Regulate Sleep
- Connecting Replication and Repair: YoaA, a Helicase-Related Protein, Promotes Azidothymidine Tolerance through Association with Chi, an Accessory Clamp Loader Protein
- UFBP1, a Key Component of the Ufm1 Conjugation System, Is Essential for Ufmylation-Mediated Regulation of Erythroid Development
- Mosaic and Intronic Mutations in Explain the Majority of TSC Patients with No Mutation Identified by Conventional Testing
- Members of the Epistasis Group Contribute to Mitochondrial Homologous Recombination and Double-Strand Break Repair in
- QTL Mapping of Sex Determination Loci Supports an Ancient Pathway in Ants and Honey Bees
- Genetic Interactions Implicating Postreplicative Repair in Okazaki Fragment Processing
- Genomics of Cancer and a New Era for Cancer Prevention
- Adaptation to High Ethanol Reveals Complex Evolutionary Pathways
- Dynamics of Transcription Factor Binding Site Evolution
- Exocyst-Dependent Membrane Addition Is Required for Anaphase Cell Elongation and Cytokinesis in
- Enhancer Runaway and the Evolution of Diploid Gene Expression
- Cattle Sex-Specific Recombination and Genetic Control from a Large Pedigree Analysis
- Drosophila Mutants Model Cornelia de Lange Syndrome in Growth and Behavior
- Pleiotropic Effects of Immune Responses Explain Variation in the Prevalence of Fibroproliferative Diseases
- Leaderless Transcripts and Small Proteins Are Common Features of the Mycobacterial Translational Landscape
- Tissue-Specific Effects of Reduced β-catenin Expression on Mutation-Instigated Tumorigenesis in Mouse Colon and Ovarian Epithelium
- Genus-Wide Comparative Genomics of Delineates Its Phylogeny, Physiology, and Niche Adaptation on Human Skin
- Mapping of Craniofacial Traits in Outbred Mice Identifies Major Developmental Genes Involved in Shape Determination
- Conserved Genetic Interactions between Ciliopathy Complexes Cooperatively Support Ciliogenesis and Ciliary Signaling
- Metabolomic Quantitative Trait Loci (mQTL) Mapping Implicates the Ubiquitin Proteasome System in Cardiovascular Disease Pathogenesis
- DNA Repair Cofactors ATMIN and NBS1 Are Required to Suppress T Cell Activation
- Spindle-F Is the Central Mediator of Ik2 Kinase-Dependent Dendrite Pruning in Sensory Neurons
- Ernst Rüdin and the State of Science
- ABCs of Insect Resistance to Bt
- Epigenetic Control of O-Antigen Chain Length: A Tradeoff between Virulence and Bacteriophage Resistance
- Encodes Dual Oxidase, Which Acts with Heme Peroxidase Curly Su to Shape the Adult Wing
- The Fanconi Anemia Pathway Protects Genome Integrity from R-loops
- Controls Quantitative Variation in Maize Kernel Row Number
- Genome-Wide Association Study of Golden Retrievers Identifies Germ-Line Risk Factors Predisposing to Mast Cell Tumours
- Insect Resistance to Toxin Cry2Ab Is Conferred by Mutations in an ABC Transporter Subfamily A Protein
- A Cytosine Methytransferase Modulates the Cell Envelope Stress Response in the Cholera Pathogen
- Conserved piRNA Expression from a Distinct Set of piRNA Cluster Loci in Eutherian Mammals
- The Multi-allelic Genetic Architecture of a Variance-Heterogeneity Locus for Molybdenum Concentration in Leaves Acts as a Source of Unexplained Additive Genetic Variance
- The lncRNA Controls Cryptococcal Morphological Transition
- Sae2 Function at DNA Double-Strand Breaks Is Bypassed by Dampening Tel1 or Rad53 Activity
- A Tandem Duplicate of Anti-Müllerian Hormone with a Missense SNP on the Y Chromosome Is Essential for Male Sex Determination in Nile Tilapia,
- Ectodysplasin/NF-κB Promotes Mammary Cell Fate via Wnt/β-catenin Pathway
- The QTL within the Complex Involved in the Control of Tuberculosis Infection in Mice Is the Classical Class II Gene
- Identifying Loci Contributing to Natural Variation in Xenobiotic Resistance in
- Variation in Rural African Gut Microbiota Is Strongly Correlated with Colonization by and Subsistence
- A Flexible, Efficient Binomial Mixed Model for Identifying Differential DNA Methylation in Bisulfite Sequencing Data
- Competition between Heterochromatic Loci Allows the Abundance of the Silencing Protein, Sir4, to Regulate Assembly of Heterochromatin
- PLOS Genetics
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- UFBP1, a Key Component of the Ufm1 Conjugation System, Is Essential for Ufmylation-Mediated Regulation of Erythroid Development
- Metabolomic Quantitative Trait Loci (mQTL) Mapping Implicates the Ubiquitin Proteasome System in Cardiovascular Disease Pathogenesis
- Genus-Wide Comparative Genomics of Delineates Its Phylogeny, Physiology, and Niche Adaptation on Human Skin
- Encodes Dual Oxidase, Which Acts with Heme Peroxidase Curly Su to Shape the Adult Wing
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání











