-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaAge-Dependent Transition from Cell-Level to Population-Level Control in Murine Intestinal Homeostasis Revealed by Coalescence Analysis
In multi-cellular organisms, tissue homeostasis is maintained by an exquisite balance between stem cell proliferation and differentiation. This equilibrium can be achieved either at the single cell level (a.k.a. cell asymmetry), where stem cells follow strict asymmetric divisions, or the population level (a.k.a. population asymmetry), where gains and losses in individual stem cell lineages are randomly distributed, but the net effect is homeostasis. In the mature mouse intestinal crypt, previous evidence has revealed a pattern of population asymmetry through predominantly symmetric divisions of stem cells. In this work, using population genetic theory together with previously published crypt single-cell data obtained at different mouse life stages, we reveal a strikingly dynamic pattern of stem cell homeostatic control. We find that single-cell asymmetric divisions are gradually replaced by stochastic population-level asymmetry as the mouse matures to adulthood. This lifelong process has important developmental and evolutionary implications in understanding how adult tissues maintain their homeostasis integrating the trade-off between intrinsic and extrinsic regulations.
Published in the journal: . PLoS Genet 9(2): e32767. doi:10.1371/journal.pgen.1003326
Category: Research Article
doi: https://doi.org/10.1371/journal.pgen.1003326Summary
In multi-cellular organisms, tissue homeostasis is maintained by an exquisite balance between stem cell proliferation and differentiation. This equilibrium can be achieved either at the single cell level (a.k.a. cell asymmetry), where stem cells follow strict asymmetric divisions, or the population level (a.k.a. population asymmetry), where gains and losses in individual stem cell lineages are randomly distributed, but the net effect is homeostasis. In the mature mouse intestinal crypt, previous evidence has revealed a pattern of population asymmetry through predominantly symmetric divisions of stem cells. In this work, using population genetic theory together with previously published crypt single-cell data obtained at different mouse life stages, we reveal a strikingly dynamic pattern of stem cell homeostatic control. We find that single-cell asymmetric divisions are gradually replaced by stochastic population-level asymmetry as the mouse matures to adulthood. This lifelong process has important developmental and evolutionary implications in understanding how adult tissues maintain their homeostasis integrating the trade-off between intrinsic and extrinsic regulations.
Introduction
Development and tissue homeostasis of multi-cellular organisms is an extraordinary cellular orchestra starting from a single zygote [1]. Cascades of cell divisions generate and subsequently maintain a great diversity of cells in an organism [2]. This life-long balance is strictly controlled and maintained through a rigid cellular hierarchy, where the stem cells lie at the apex of the division cascades [3].
Stem cells are a group of cells with a dual role. On one hand, they need to maintain their own population through self-renewal. On the other hand, stem cells also give rise to differentiated cells which carry out most body functions [4]. In order to fulfill the dual role of self-renewal and differentiation, stem cells can undergo two different modes of cell division – asymmetric and symmetric [5]. In the asymmetric division mode, one daughter cell is maintained as the stem cell and the other goes on and evolves into terminally differentiated cells. The stem cells can also divide symmetrically, leading to either two stem cells or two differentiated cells.
Asymmetric division is particularly attractive and allows stem cells to accomplish both maintenance and differentiation simultaneously in a single division. However, symmetric divisions are also indispensable in situations such as morphogenesis and tissue injury where stem cells need to proliferate rapidly [6], [7]. A robust balance between proliferation and differentiation must be maintained to prevent aberrant growth on one hand and tissue loss on the other [5].
Stem cells often form distributed clusters and live in local nurtured structures known as the stem cell niches [8], [9]. In order to maintain a static hierarchy between different cell types, two different strategies can be employed. In the first strategy (also called cell asymmetry) [10], stem cells engage only in asymmetric divisions where dual roles of self renewal and differentiations can be successfully fulfilled while keeping the stem cell number constant. Population level equilibrium is achieved by maintaining a stasis at the single cell level through asymmetric cell divisions. Studies looking at invertebrate systems, in particular Drosophila melanogaster and Caenorhabditis elegans, have found a predominance of asymmetric divisions where stem daughter cells remain within the niche and differentiated cells exit and evolve into functional cells [11], [12]. Biological evidence for cell asymmetry is quite strong in many invertebrate systems [10]. In the other extreme (also called population asymmetry), each stem cell division gives rise to one stem cell and one differentiated cell on average [10]. Homeostasis is maintained by having a subset of cells proliferate while other stem cells are lost through differentiation. If the gain and loss are balanced, stasis is achieved at the population level rather than at the level of individual cell divisions [13]. In contrast to invertebrates, it appears that population asymmetry is more prevalent in mammals [14].
Mammalian intestine has become one of the best model systems for studying stem cell dynamics [15]–[18]. Powerful genetic tools together with recently-identified intestinal stem cell markers enable us to directly trace stem cells [19]–[21]. As a result, dynamics of cell populations are becoming accessible to investigation [22]. Interestingly, the relative prevalence of symmetric and asymmetric divisions among studies conducted to date is not yet clear. On one hand, lineage tracing techniques together with models from statistical physics reveal a pattern of neutral drift in a group of equipotent stem cells [23], [24]. Population asymmetry with a predominance of symmetric divisions is the major mode of stem cell renewal in the adult mouse intestinal crypt. On the other hand, optimal control theory together with experimental data indicates that early development of the mouse intestinal crypt is achieved by a surge of symmetric divisions establishing the stem population followed by a transition to predominantly asymmetric divisions [25]. Moreover, molecular evidence for asymmetric division is starting to accumulate, suggesting that the role of asymmetric divisions might be underappreciated [26]. The dynamics of stem cell renewal, in particular the balance between cell asymmetry and population asymmetry of stem cells, remain enigmatic.
Genomic sequencing, in particular single cell sequencing, provides a powerful alternative approach for studying cell lineage relationships. Compared to traditional molecular techniques such as the lineage tracing [27], spontaneous somatic mutations provide a natural internal cell marker for tracing relationships in a group of cells. In this work, we use a previously published dataset comprising single-cell sequence information collected from mouse intestinal crypts [28]. The authors of this study sequenced multiple microsatellite markers in a repair-deficient mouse strain (Mlh1−/−) [28], [29]. The reduced efficiency of DNA repair machinery results in higher microsatellite mutation rate and thus increased genetic variation, allowing us to discern genealogical relationships in this group of cells. Using traditional phylogenetic methods, the authors of the previous study found that intestinal crypts do not support the immortal strand hypothesis. Instead, they found support for the existence of monoclonal conversion, a process by which multiple crypt cells drift toward monoclonality, where offspring population is only derived from a single ancestor [28].
Population-genetic theory [30], in particular coalescent theory [31], [32], provides a natural framework for studying cells in a population. Population dynamics driven by a combination of symmetric and asymmetric divisions can be explicitly modeled. When we take a sample of cells from a tissue, there will be a genealogical relationship relating individual cells to their common ancestor [33]. The shape of this genealogy is governed by the mode of cell division and thus carries information about underlying population dynamics. In reality, we do not directly observe the genealogy, but rather genotype information (e.g. microsatellite markers presented here) collected from individual cells. By considering all possible ancestral relationships compatible with a given pattern of genetic variation (instead of just a single gene genealogy in the phylogenetic framework [28]), we can infer the underlying balance between symmetric and asymmetric divisions using statistical modeling. Here, we demonstrate that this approach, based on classical population genetics, can provide powerful insights into cellular dynamics within an organism and supply fine-scale quantitative description of the processes underlying cellular homeostasis.
Results
A population-genetic model with stem cell division mode and coalescent
We consider a discrete-generation model of tissue homeostasis. In each cell generation, a proportion α of the cells divides symmetrically and gives rise to two descendant stem cells (type I, Figure 1A). A fraction β of the cells divides asymmetrically (type III) and 1-α-β cells divide symmetrically and produce two differentiated cells (type II). Because type II divisions do not give rise to any stem cell descendants, the number of stem cells in generation t will be Nt = (2α+β)t×N0, where N0 is the population size at time 0.
Fig. 1. Anatomy of intestinal crypts and coalescent processes for the two-deme model. 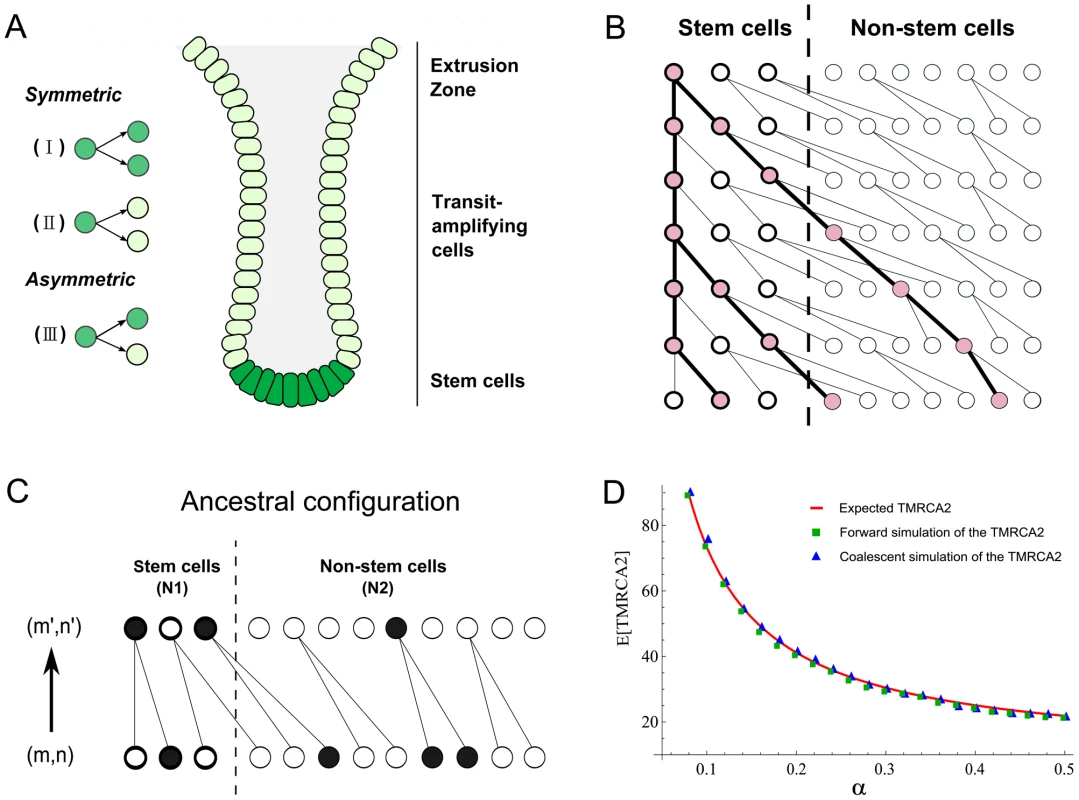
(A) Anatomical structure of the intestinal crypt. The dark green cells represent stem cells and light green cells are transit-amplifying cells. There are three types of stem cells divisions (I, II and III, see main text). (B) A cartoon illustration of a coalescent process in the two deme model. One cell from stem cell deme and two cells from the transit-amplifying cell deme were sampled. Their ancestral relationship is depicted as the gene tree connecting their ancestors. (C) The state transition for the Markov Chain in one step. The current state of the chain is (m,n) and the state in the previous generation is (m′,n′). In the example here, (m,n) = (1,3) and (m′,n′) = (2,1). (D) The expected time to the most recent common ancestor for two lineages (denoted as TMRCA2) was calculated using three different approaches. The solid line is calculated using a first-step analysis of the Markov Chain. Blue squares are the results from the forward simulation and triangles are from the direct simulation following the Markov Chain. Now, suppose we pick two stem cells at random at time t, the probability that they will have a common ancestor in the previous generation can be computed in two steps. The first stem cell picked must be derived from the type I stem cell division in the previous generation and the probability of picking it is 2α/(2α+β). Secondly, the other sampled stem cell must be the pair of the first picked stem cell in the type I division and the probability of picking it is 1/(Nt−1). Thus the probability of finding a common ancestor (i.e. a coalescence) in a single generation backwards in time for two stem cells is:
The number of stem cells in intestinal crypts is approximately constant. We thus assume that 2α+β = 1 and Nt = N0 = N. Then, the above probability can be rewritten as 2α/(N−1). Once we have this single-step probability, other quantities such as the time to the most recent common ancestor for two cells and the coalescent relationship in a sample can be derived following the n-coalescent approach (Materials and Methods) [31], [32]. In this parameterization, both cell asymmetry and population asymmetry are special cases of a general model. For example, strict cell asymmetry will correspond to cases where β = 1. This general framework will allow us to test and pick the best models based on empirical observations.A two-deme population-genetic model for intestinal crypts
Each intestinal subunit is composed of two parts: a protrusion compartment called villus, which contains terminally differentiated cells, and an invagination compartment named crypt, which hosts stem cells and highly proliferative transit-amplifying cells. There is a continuous process that replaces functional cells in the villi with cells grown out of the crypts. We used a two-deme population-genetic model to capture continuous renewal of stem cells and transit-amplifying cells (Figure 1A). In each generation, the stem and non-stem cell population follow a dynamic process as described in the previous section. The only exception is that differentiated descendants from the stem cell deme (population 1) are constantly migrating into the other population (transit amplifying cell deme) (Figure 1B). One-way migration in the two-deme population model reflects the coupling of the stem and non-stem populations in the intestine.
In practice, when we take a random sample of cells from a crypt, we do not know whether they are stem or differentiated cells. Thus, the number of sampled cells from two demes (denoted as (m, n)) will follow a hypergeometric distribution (N1, N2, m+n), where N1 and N2 are population sizes for the two demes. Given (m,n) cells from deme 1 and deme 2, the coalescent process of going backwards in time and finding common ancestors for these lineages can be modeled using a Markov Chain (Figure 1B and 1C). The transition probability between neighboring states can be calculated as a combination of individual coalescence or migration events. For example, a single coalescence and one migration event in deme 2 will change the state from (m,n) to (m+1,n−3) (Figure 1C). For the sake of computational efficiency, we only consider transitions involving a maximum of two events (either coalescence or migration). Probability of three events occurring in one transition is low and is neglected in our calculations (Text S1). Similar to previous studies [34], when we compare the Markov Chain results with exact calculations performed through forward simulations, we find that approximate results provide an accurate characterization of the underlying dynamics (Figure 1D, Materials and Methods). Thus, a two-deme population-genetic model and the associated coalescent process can be used to model dynamics underlying cellular homeostasis of the intestinal crypt.
Likelihood calculation and Monte Carlo Integration
Given observed genotype information (e.g. microsatellite markers, denoted as D), obtained by assaying single cells, the likelihood of the data can be calculated as
where θ is the set of model parameters, including symmetric/asymmetric division parameters (α, β) and the population size parameters (N1,N2). The G (i.e. gene genealogy) represents coalescent relationships in a sample of cells. In Eq.2, the Pr(D|G) can be computed using standard phylogenetic methods and the pruning algorithm can be employed to evaluate this term [35]. The Pr(G|θ) can be calculated from the coalescent process using a Markov Chain or forward simulation (see the following sections). Since we do not directly observe the underlying gene genealogy, we need to take into account all possible ancestral relationships that are compatible with the data in order to evaluate the likelihood. By integrating over all these genealogies, the likelihood of observed data can be calculated as a function of the underlying parameters (Eq.2).In practice, given the large dimensionality of genealogical spaces, it is not feasible to exhaustively explore all possible ancestry relationships in a sample. Instead, we use a Monte-Carlo approach to compute the likelihood in Eq.2:
where Gi is sampled from Pr(G |θ). It can be shown that, as k increases, likelihoods from Eq.2 and Eq.3 will converge to the same value in the limit [36].Sampled gene genealogies can be drawn either from the Markov Chain or forward simulations depending on whether a cell population has reached equilibrium (i.e. stationary distribution) at the time of data acquisition. Markov Chain calculations assume that a given population has reached equilibrium under a given configuration of symmetric/asymmetric division rates, which may not always be true. On the other hand, forward simulation can be applied to either non-stationary or stationary scenarios, but is computationally much more expensive.
Through computational simulations, we found that stationarity has been reached for samples taken on day 340 across most of the parameter space, but not on day 52 (Text S1). Therefore, we generated genealogies for those non-stationary scenarios by simulating a crypt population history with a phase of crypt morphogenesis, followed by a period of homeostatic renewal (Materials and Methods) [25]. The generation number for the associated time point is calculated as the number of cell divisions within a given amount of time. For example, the stem cells are dividing at a rate of about once every 22 hours [25] (Materials and Methods). Since genealogical relationships are directly recorded during the course of the computer simulation, simply picking a sample of cells at the end of a simulation run yields a sample from the distribution of gene genealogies.
After averaging over many possible genealogical histories, we can calculate the likelihood of the observed data (i.e. microsatellite markers). Given the likelihood function, maximum likelihood approaches can be employed to infer the most likely parameter values. In particular, we are interested in estimating the proportion of symmetric/asymmetric divisions (α, β) in the life history of mice.
Single-cell data and the statistical inference
Single-cell genotype data were taken from a previous study [28]. Two mice from a DNA repair deficiency strain (Mlh1−/−) with much elevated mutation rates [28], [29] were sacrificed at two different ages (day 52 and 340). From each mouse, two crypts were harvested from the mouse colon. Multiple cells (4–6, Table 1) were subsequently isolated from each sample and sequenced at a set of micro-satellite markers.
Tab. 1. Maximum-likelihood estimates asymmetric division rate. 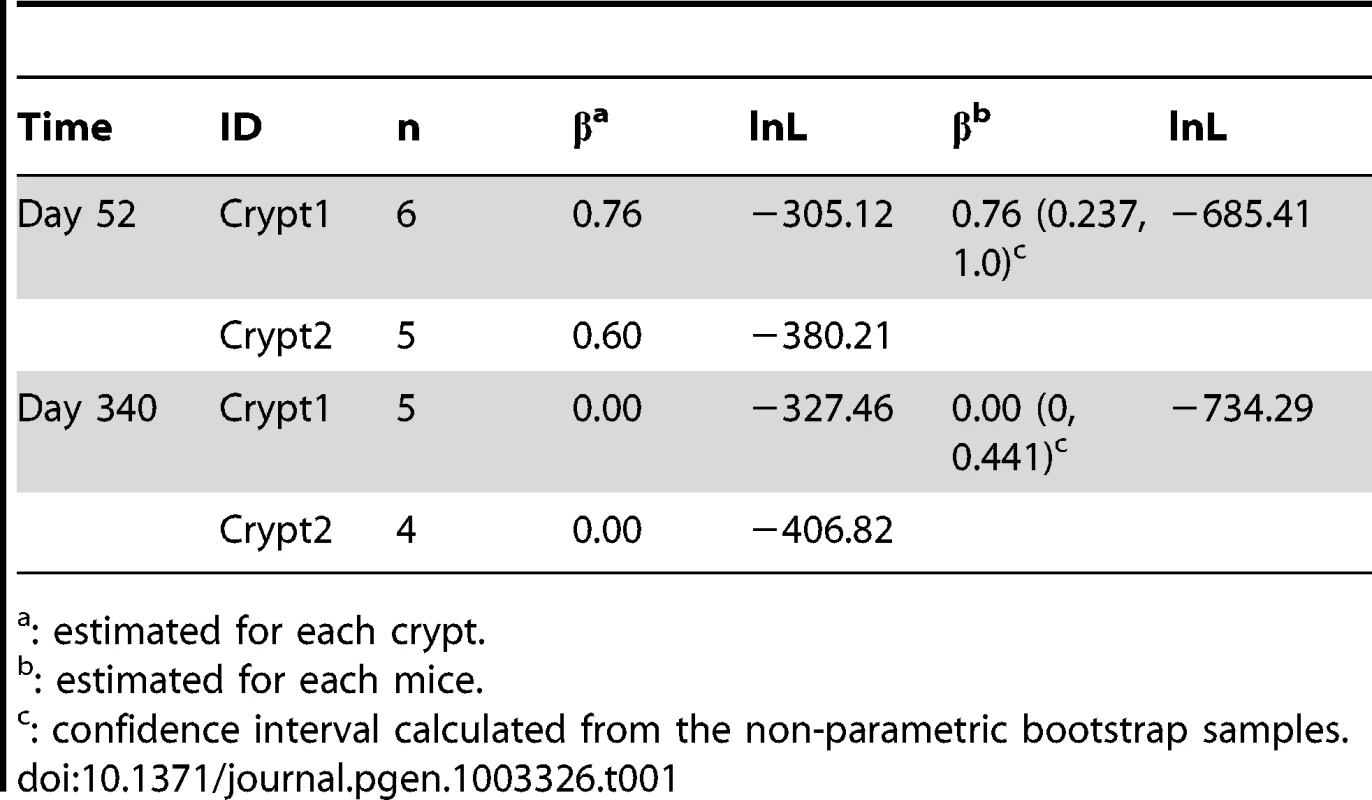
: estimated for each crypt. Using a two-step mutation model for micro-satellite markers, we first calculated the genetic distances between all sampled cells (Materials and Methods). As shown in Figure 2, individual cells within an intestinal crypt are monophyletic and are clonally related. Between-crypt divergence rapidly increases with age (Figure 2B), in agreement with previous observations of fast clonal turnover in intestinal crypts [23].
Fig. 2. Phylogenetic relationships for the crypt single cells and likelihood curve for the proportion of asymmetric divisions. 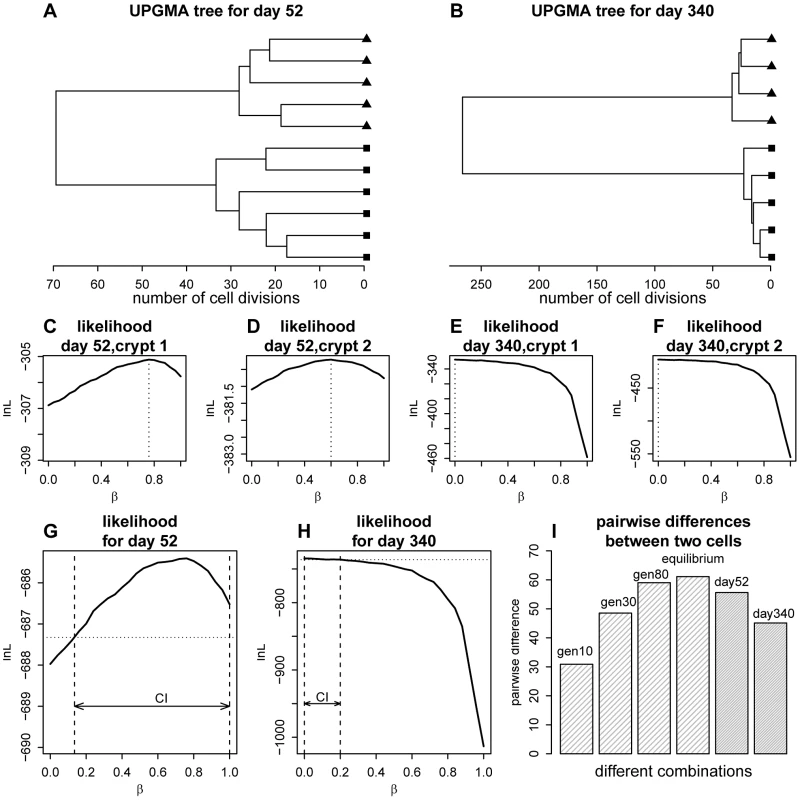
(A) Unweighted Pair Group Method with Arithmetic mean(UPGMA) tree [66] for the cells sampled from the two crypts at day 52. Distances were calculated using the two-step mutation model. (B) UPGMA tree for day 340. (C) Likelihood curve as a function of the proportion of asymmetric divisions for one of the crypts at day 52. (D) The same plot as panel C, but for the other crypt at day 52. (E) Likelihood curve as a function of the proportion of asymmetric divisions for one of the crypt at day 340. (F) The same plot as panel E, but for the other crypt at day 340. (G) Likelihood curve as a function of the proportion of asymmetric divisions for day 52 (combining two crypts). The horizontal dashed line marks the level of likelihood that is 1.92 units (0.5×) below the maximal value. The confidence interval (CI) for the proportion of asymmetric division rate is shown as the arrow between the two vertical dashed lines. (H). Likelihood curve as a function of the proportion of asymmetric divisions for day 340 (combining two crypts). The horizontal dashed line marks the level of likelihood that is 1.92 units below the maximal value. The confidence interval (CI) for the proportion of asymmetric division rate is shown as the arrow between the two vertical dashed lines. (I) A demonstration of the phenomena that the gene tree will increase in size as the crypt population reaches equilibrium (stationarity). The genealogical tree size (indicated as the mean pairwise divergence for two randomly picked cells) at different cell generation (generation 10, 30, 80 as well as equilibrium point) for the crypt population are shown (β = 0.4). The observed pairwise divergence for day 52 and day 340 are also plotted. Using the likelihood approach we outlined above, we calculated the likelihood of the data as a function of asymmetric division rate for each crypt (Figure 2C–2F). For example, using the two crypts sampled from day 52 mice, maximum-likelihood estimates for the proportion of asymmetric divisions are 0.76 and 0.60 respectively (Figure 2C–2D). Interestingly, when we look at stem cells from the older mice (day 340), maximum-likelihood estimates are 0, which means that stem cells are all dividing symmetrically (Figure 2E–F). When we combined the data from both crypts at each life stage, maximum-likelihood estimates for proportions of cells dividing asymmetrically at day 52 and 340 are 0.76 and 0.0 respectively (Figure 2G–H). Our analyses thus suggest that the stem cell populations have changed from largely asymmetric divisions to solely symmetric ones.
Even though the point estimates of the asymmetric division rate is rather different, the confidence in the point estimates is not very strong. This is especially true for the day 52 (Figure 2G). In order to assess the uncertainties in the point estimates, a resampling-based nonparametric bootstrap analysis was conducted [37] (Materials and Methods). As shown in Table 1, the estimates for the asymmetric division rates at these two time points stay quite disparate, even though the confidence intervals overlap with each other. In order to compare these two point estimates rigorously, we explicitly tested the null hypothesis of H0: β52 = = β340 against the alternative hypothesis Ha: β52≠β340. Since the null hypothesis is a special case of the alternative hypothesis (i.e. the models are nested), a Likelihood Ratio Test (LRT) can be employed to ask whether the null hypothesis can be rejected with confidence. After we calculated the associated test statistic, the LRT gives the p-value of 0.024, which is significant at the nominal cut-off of 5% (Table 2). Statistical significance is also observed when we compare β52–β340 with zero over the bootstrap samples (Figure S1, P = 0.04). In other words, there is strong statistical evidence that the proportion of cells undergoing asymmetric divisions is very different between day 52 and 340.
Tab. 2. Likelihood ratio tests under different models. 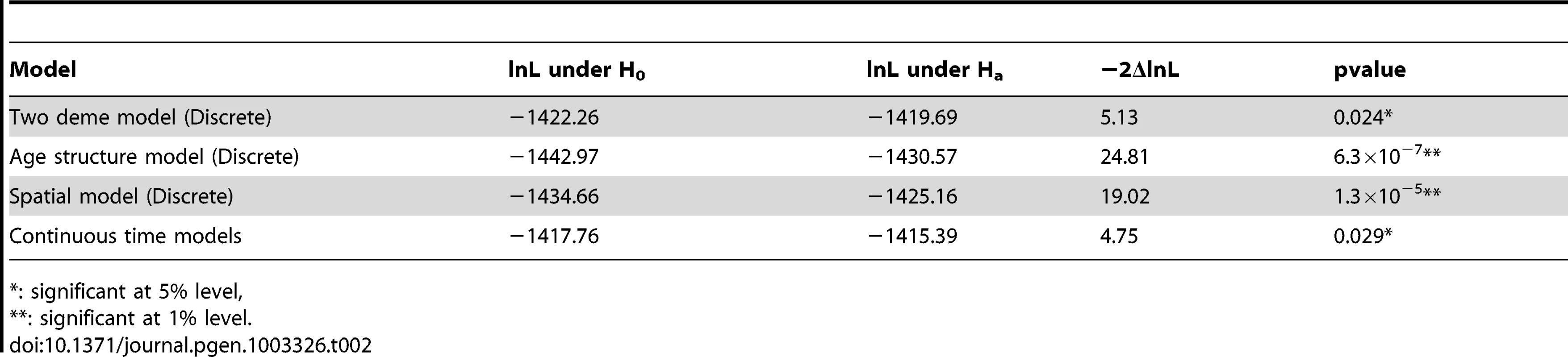
: significant at 5% level, In addition to the two-deme model outlined above, we explored a series of more complicated models that reflect various additional aspects of crypt biology. In general, due to complexity of these models, analytical results are much harder to derive, but can be supplemented with computer simulations (Materials and Methods). For example, when we compute the log-likelihood under a model where the population of the transit-amplifying cell pool is age-structured (Table 2, Figure S2), the likelihood ratio test shows even stronger evidence of differences in asymmetric division rates between day 52 and 340 (P = 6.3×10−7). This is also true when we explore spatial structures of the intestinal crypt (P = 1.3×10−5, Table 2, Figure S2), as well as continuous-time models where waiting times between events are exponentially distributed and population sizes are allowed to fluctuate within a certain range (P = 0.029, Table 2, Figure S3). In addition, we also examined possible variations in mutation rates and found that the results stay qualitatively similar (Materials and Methods, Text S1). In summary, the conclusion that stem cells transition from asymmetric to symmetric division is insensitive to model details.
Discussion
Using population genetic theory, in particular the coalescent theory, we have drawn an extraordinary dynamic picture of intestinal crypt homeostasis. Compared to earlier lineage-tracing methods which typically do not allow for individual lineage relationships, this branch of theory provides a more detailed picture of stem-cell crypt dynamics. With single-cell data collected from different life stages, we found strong statistical support for a transition from cell asymmetry to population asymmetry during mouse life history.
Intuitively, the reason we can observe this discrepancy is that genealogical trees of crypt cell populations will steadily increase in size as the population evolves to establish equilibrium. This is analogous to the founder population effect in population genetics (Figure 2I). The genealogical trees for day 52 (before equilibrium) are expected be much shorter than those from later times if asymmetric division parameters are constant. However, the gene trees at day 52 are observed to be larger than those at day 340 (Figure 2I). The discrepancy between expectation and real observation leads to the inference of higher asymmetric division rate at the early life stage, because asymmetric division will slow down stem cell lineage turnovers and increase genealogical tree size.
Previous observations revealed that mouse crypt morphogenesis started with a surge of symmetric divisions establishing the pool of stem cells, followed by a transition to predominantly asymmetric divisions that maintain an equilibrium between stem cell self-renewal and differentiation [25]. Our results support the existence of a second transition from mostly asymmetric stem cell divisions to symmetric divisions during intestinal homeostasis (Figure 3A). It remains to be seen whether this phenomenon also occurs in other systems.
Fig. 3. Lifelong equilibrium for stem cell symmetric/asymmetric divisions. 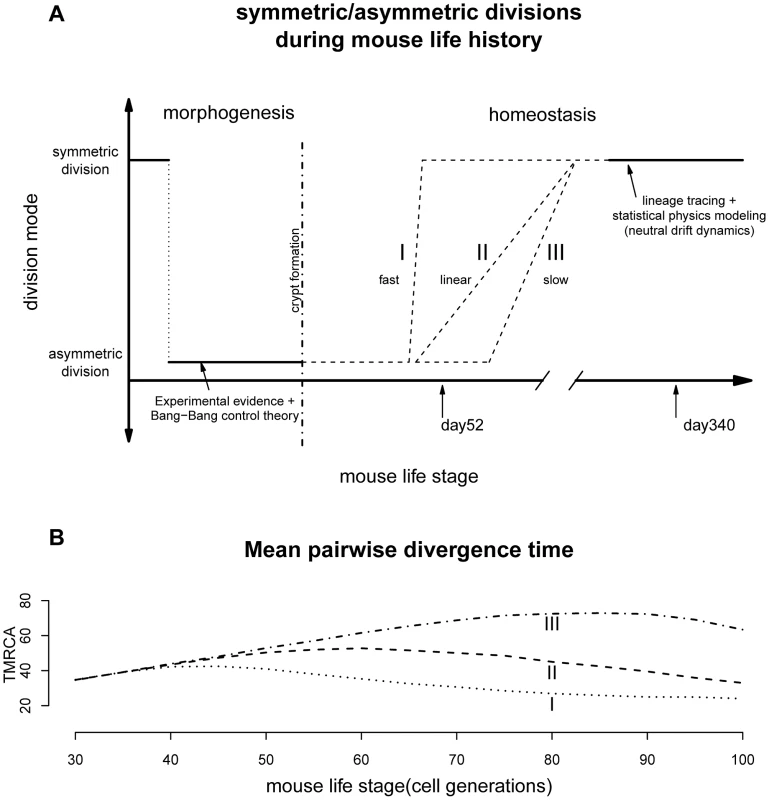
(A) The proportion of asymmetric and symmetric division as a function of mouse life stage. The pattern from morphogenesis are from experimental data together with the optimal control theory prediction [25]. The lineage tracing evidences are from two earlier studies [23], [24]. The transition from cell asymmetry to population asymmetry can take a variety of forms, including I) a fast switch similar to the Bang-Bang control, II) a linear accumulation, III) slow progression depending on the interplay between intrinsic and extrinsic signals. (B) When simulating crypt histories using curve I, II and III in Figure 3A and plotting mean pairwise divergence time between two random cells (a measurement of genealogical length), the average pairwise divergence shows very different trajectories under different transitional history. The population asymmetry found here for day 340 matches previous observations that adult intestinal stem cells are maintained by replacing randomly-lost cells through predominately symmetric divisions of their neighbors (Figure 3A) [23], [24]. This random neutral drift also allows monoclonal turnover observed previously [28]. The stochastic fate determination of stem cells seems to be quite general across many tissue types and species [13], [14], [38].
Our observations raise a number of questions about the dynamics of the transition between cell division modes. Stem cell behaviors are often controlled by both internal signals (e.g. cellular polarity [39] or telomerase activity [40]) and external factors (e.g. BMP pathway in the mesenchyme) [16], [18], [41]. What are the relative roles of these intrinsic and extrinsic factors are still not fully understood and therefore the exact molecular mechanisms behind the transition between cell division modes are still unknown.
Furthermore, transition timing is also unclear. If paneth cells are responsible for maintaining much of the intestinal niche [42], the transition might be quite fast since stem niche and stem cells are derived from the same cell cascade where an upstream triggering signal can easily be propagated downstream and the transition can be hastened through a snow-ball-like effect (Figure 3A). On the other hand, if signals from other mesodermal components (e.g. mesenchyme) are also contributing to this transition, we might imagine the stem cell and their niche could be changing asynchronously leading to a variety of histories with drastically different paces [43], [44].
Interestingly, current biological evidences seem to have a tilt towards a fast transition. For example, lineage tracing study looking at the speed of drift towards monoclonality, has found similar rates for mice of age 1.5, 6.5 as well as 8 months [23]. In other words, starting from about 45 days, the crypt dynamics could potentially have shifted to largely symmetric divisions. In our model we were treating asymmetric/symmetric parameter as a fixed unknown constant and the coalescent analysis is a retrospective approach looking at the profile of a recent history before the time of observation (typically within 4N generations, where N is the population size [30]). Our results thus reflect a time-average measurement. The fast transition might have lead to the statistical uncertainties for the asymmetric division rate observed for day 52. Nevertheless, based on our limited simulations with time-varying asymmetric division rates, changes in transition dynamics should leave very different genealogical signatures, where future studies with dense sampling across time will be able to resolve this landscape more precisely (Figure 3B). After all, the pattern observed here seems to suggest that the switch has started not long before day 52, which is broadly around mouse maturation (Figure 3 and following sections).
Why do the crypt cells need to switch to population level asymmetry, which is an apparently more fragile scheme for long-term tissue maintenance [10]? There are two possible explanations for this transition. One explanation involves acquisition of the population asymmetry driven by adaptive mechanisms. Asymmetric divisions may be a harder task for cells to perform as cell fate determinants all need to be delivered to the two daughter cells according to the two distinct states [5]. In contrast, the easier mode may be symmetric divisions in which the two daughter cells need not be distinguished. The implication for the transition is that as mice grow old, their cells gradually take the easier mode. In addition, since stem cell function often declines with age, population asymmetry might allow stem cells to effectively repair and restore homeostasis – a key adaptation that can increase capacity for repair and increase life-span [45]. Furthermore, adaptive immune response to environmental insults including gut microbiota infection can also possibly contribute to the homeostatic transition [44], [46], [47]. In light of this view, cancer and tissue loss, two flip sides of normal cellular dynamics, might result from disruptions of this cell division equilibrium [5], [48].
On the other hand, there might also exist a “passive” explanation for this transition. The observed progression can simply be a by-product of natural selection. When a single gene has multiple functions, some of the functions will be beneficial to the organism, while others might be detrimental. Most importantly, when the advantageous gain outweights the deleterious costs, the target gene can still be selected (i.e. antagonistic pleiotropy) [49]. During the course of evolution, a gene with multiple effects will be strongly optimized for its function before reproduction, and as a consequence also produce deleterious effects in later life [49]. In this light it is notable that the transition in cell division mode occurs roughly at the time of sexual reproduction (Figure 3). Many proteins involved in asymmetric cell divisions also function as tumor suppressor genes [5], [50], [51]. The loss of asymmetric division might thus simply be driven by the increasing need for active tumor suppressors [52].
The life-history of stem cell division is not yet fully discernable from our results (e.g. Figure 3). For example, our estimate of the proportion of asymmetric divisions for day 52 is still quite high, even though we have evidence that the proportions at days 52 and 340 are significantly different. Information collected from only two time points also prevents sophisticated models where many of the parameters can be treated as time-varying variables rather than fixed constants. Future studies with denser serial sampling together with larger number of crypts might be able to draw a more concrete picture of the crypt homeostasis.
Until now, asymmetric divisions were thought to be rarer in vertebrates than invertebrates [5]. However, new evidence for the existence of this mode is starting to accumulate for a few tissue types such as the central nervous system [53], skin [54], [55], the hematopoietic system [51], [56], [57] as well as the intestinal crypts [26]. Since the mechanisms controlling stem cell symmetric and asymmetric divisions are often conserved across the tree of life [16], the pattern observed here for the mouse intestine is very likely to be quite general. With the advances in genomic technology, in particular whole-genome single-cell sequencing [58], [59], we should be able to reveal a more lively cellular orchestra across a wide range of organ types and species, each with its own mechanism and equilibria.
Materials and Methods
Population dynamics for cells within intestinal crypts
Since population sizes are relatively constant in the intestinal crypt and because type III divisions do not change the number of stem cell descendants, the proportions of two types of symmetric divisions (type I and II) have to be balanced and are set to be equal so that the total number of cells is maintained (Figure 1A). In other words, 1-α-β (proportion of type II divisions) is be equal to α (proportion of type I divisions). In each generation, fraction α of the stem cells divides symmetrically, each cell giving rise to two stem cells (type I); fraction β divides asymmetrically (type III) and fraction α divides symmetrically with each cell producing two differentiated cells (type II). Differentiated cells from both asymmetric and symmetric divisions migrate to the transit-amplifying cell pool.
Since there is a constant extrusion of cells from the crypt into the villi, we capture the dynamics of the transit-amplifying cell pool by allowing only a certain proportion of the cells to participate in reproduction for the next generation. The remaining cells are extruded out of the deme 2. We set the population size of stem cells (population 1) to N1 and that of transit-amplifying cells (population 2) to N2. In each generation there are N1 cells migrating to the transit-amplifying cell pool. In the transit-amplifying cell population, fraction γ of N2 cells divide once and give rise to two descendant cells. The remaining (1−γ)×N2 cells are extruded outside of the population 2. The value of γ is set to (N2-N1)/2N2 such that the population size in population 2 is constant. Based on previous observations in mouse colon crypts [60], [61], we set the population size N1 and N2 to be 15 and 185. Population sizes such as 250 (15 stem and 235 non-stem cells) are also tried and results stay similar.
Genealogical histories, Markov Chain, and the forward simulation
Given the number of cells we sampled in two demes, the process of going backwards in time and finding common ancestors can be modeled as a Markov Chain. The state transitions are given by combinations of individual coalescence or migration events. For two randomly sampled lineages, the expected time to their most recent common ancestor (MRCA) can be computed by directly simulating from a Markov Chain following the appropriate state transitions. The expected value for the time to MRCA for two lineages can also be derived analytically using a first-step analysis of a given Markov Chain (Figure 1D). In Text S1, we presented the details of the transition probabilities between state spaces for the Markov Chain.
The Markov Chain calculation assumes that data are collected from a stationary process. Based on our simulations, we find that, for most of the parameter values, stationary distributions have been reached by day 340. However, this does not appear to hold for day 52 (Figure S4 and Text S1). In these cases, forward simulations are used to generate genealogical histories from Pr(G|θ). To achieve this, we simulated population histories with two phases: morphogenesis and homeostasis (Figure 3). This scenario was chosen to reflect experimental evidence as well as predictions from the Bang-Bang control theory [25]. In this process, the intestinal crypt is founded by first creating N1 stem cells, followed by a series of asymmetric divisions to generate the transit-amplifying cell population. After crypt morphogenesis, populations follow the dynamic process described in the previous section. At the end of our simulations, a random subset of cells is sampled and their genealogical history is recorded (see Text S1 for details).
To estimate the number of generations leading to day 52, we tried a series of approaches. Since we know that crypt morphogenesis starts around post-natal day 7 for mice [62], [63] and stem cells divide every 22 hours [24], [25], postnatal day 52 corresponds to about generation 50 starting from crypt morphogenesis (roughly 42 generations after crypt formation because crypt morphogenesis takes around 8 generations). Because the exact cell generation number will be a random variable around this mean value, we used various forms of random distributions (e.g. beta distribution or truncated normal distribution) to model the generation number. Conditioning on the generation number, gene genealogies in the forward simulation at the corresponding generation number is sampled for the Pr(G|θ) at day 52. (see Text S1 for details).
Single-cell data acquisition
Data were taken from a previously-published study [28] where multiple single-cell genotypes were sequenced from a DNA-repair deficiency mouse strain (Mlh1−/−). This strain has elevated mutation rates, allowing for enough informative mutations to enable our analyses [28], [29]. Two mice at day 52 and 340 were sacrificed. From each mouse, two crypts were harvested from the mouse colon. Multiple cells (4–6, Table 1) were then isolated and sequenced at a set of micro-satellite markers. In total, 150 microsatellite markers were genotyped, from which only markers with successful genotyping information from at least two cells were extracted for this work (70–90 markers).
Alternative models and genealogical histories
We also tried a series of alternative models to explore other aspects of stem cell dynamics.
In the age structure model (Figure S2A), multiple demes exist in the transit amplifying cell population. Each of these demes corresponds to cells with different ages (number of divisions since leaving the stem cell deme). Cells hitting an age limit will be extruded out of the crypt. In the spatial model (Figure S2B), multiple spatial demes corresponding to cells at different localities are constructed. Demes in the transit amplifying cell population have different probability of being extruded from the crypt depending on their physical locations.
In the continuous-time models, the time to the next event (waiting time) is exponentially distributed with the intensity parameter specified by the cell division rate (λ). The time to the next event for n cells is exponentially distributed with rate nλ. Given the time to the next event, the exact cell that experiences this event is randomly picked among the n cells following statistical properties of the Poisson Process [64]. When a stem cell is picked, the possible events are type I/II/III stem cell divisions, depending on the values of α and β. If a transit-amplifying cell is picked, it either divides or is extruded out of the crypt with the associated probability. In this simulation, we allowed the stem cell population to fluctuate within a size range (size from 10 to 20 with a mean of 15), a feature we implemented using rejection sampling [64]. The details of these models are presented in Text S1.
In general, analytical results from these models are much harder to derive, but computational simulations can be conducted to sample gene genealogies from the random process. Likelihood calculations follow the same procedures as previous models after sampling gene genealogies from Pr(G| θ).
Pruning algorithm, the mutational model, and the UPGMA tree
Given a gene tree, the likelihood of the observed data can be computed from the tip of the tree towards the root using the pruning algorithm [35]. For the microsatellite loci, we used a two-step mutational model where repeat number j can mutate to j±1 and j±2. Previous empirical measurements have found that the average mutation rate is 0.01 per site per generation and size-two transitions (j±2) are happening at 1/7 the frequency of size-one mutations (j±1) [28]. We also explored other mutational models and they did not affect our conclusions (data not shown).
In order to further explore the possibility of mutation rate variation, we used various forms of the beta distribution to capture uncertainty in the mutation rate. Since the mutation rate measured from previous studies is 0.01 per site per generation, we adopted beta distributions with different shape parameters, but transformed to take values between 0.0075 and 0.0125. The likelihood of the data can be calculated by partitioning the mutation distribution into discrete bins and taking the weighted sum of individual likelihoods calculated at discrete values of mutation rates [65] (see Text S1).
Unweighted Pair Group Method with Arithmetic mean (UPGMA) tree [66] was built using functions implemented in the APE (Analyses of Phylogenetics and Evolution) library [67] within the R package (http://www.R-project.org). The pairwise distances between the cells were calculated using the mutation matrix specified in the previous section.
Statistical inference
The likelihood of the data as a function of the underlying parameters can be computed in a Monte Carlo fashion as in Equation 3. We sampled 20,000 gene genealogies to compute the log-likelihood for each combination of parameter values. A non-parametric bootstrap test was conducted by resampling microsatellite markers from the original dataset with replacement (100 replicates) and re-running the analyses. In the likelihood ratio test, the maximum-likelihood values under the null and alternative model respectively are extracted. Likelihood Ratio Test (LRT) is conducted by comparing twice the log-likelihood ratio to the chi-square distribution with one degree of freedom, since the two models we compared were nested with the alternative having one extra parameter.
Supporting Information
Zdroje
1. Wolpert L, Tickle C (2010) Principles of Development. Oxford University Press, USA.
2. Cannon WB (1963) Wisdom Of The Body. W. W. Norton and Company, Inc.
3. BeckerAJ, McCE, TillJE (1963) Cytological demonstration of the clonal nature of spleen colonies derived from transplanted mouse marrow cells. Nature 197 : 452–454.
4. MooreKA, LemischkaIR (2006) Stem cells and their niches. Science 311 : 1880–1885.
5. MorrisonSJ, KimbleJ (2006) Asymmetric and symmetric stem-cell divisions in development and cancer. Nature 441 : 1068–1074.
6. DoetschF, CailleI, LimDA, Garcia-VerdugoJM, Alvarez-BuyllaA (1999) Subventricular zone astrocytes are neural stem cells in the adult mammalian brain. Cell 97 : 703–716.
7. KimbleJE, WhiteJG (1981) On the control of germ cell development in Caenorhabditis elegans. Dev Biol 81 : 208–219.
8. LiL, XieT (2005) Stem cell niche: structure and function. Annu Rev Cell Dev Biol 21 : 605–631.
9. SchofieldR (1978) The relationship between the spleen colony-forming cell and the haemopoietic stem cell. Blood Cells 4 : 7–25.
10. WattFM, HoganBL (2000) Out of Eden: stem cells and their niches. Science 287 : 1427–1430.
11. KnoblichJA (2008) Mechanisms of asymmetric stem cell division. Cell 132 : 583–597.
12. MorrisonSJ, SpradlingAC (2008) Stem cells and niches: mechanisms that promote stem cell maintenance throughout life. Cell 132 : 598–611.
13. ClaytonE, DoupeDP, KleinAM, WintonDJ, SimonsBD, et al. (2007) A single type of progenitor cell maintains normal epidermis. Nature 446 : 185–189.
14. SimonsBD, CleversH (2011) Strategies for homeostatic stem cell self-renewal in adult tissues. Cell 145 : 851–862.
15. BjerknesM, ChengH (1999) Clonal analysis of mouse intestinal epithelial progenitors. Gastroenterology 116 : 7–14.
16. CrosnierC, StamatakiD, LewisJ (2006) Organizing cell renewal in the intestine: stem cells, signals and combinatorial control. Nat Rev Genet 7 : 349–359.
17. MarshmanE, BoothC, PottenCS (2002) The intestinal epithelial stem cell. Bioessays 24 : 91–98.
18. van der FlierLG, CleversH (2009) Stem cells, self-renewal, and differentiation in the intestinal epithelium. Annu Rev Physiol 71 : 241–260.
19. el MarjouF, JanssenKP, ChangBH, LiM, HindieV, et al. (2004) Tissue-specific and inducible Cre-mediated recombination in the gut epithelium. Genesis 39 : 186–193.
20. IrelandH, KempR, HoughtonC, HowardL, ClarkeAR, et al. (2004) Inducible Cre-mediated control of gene expression in the murine gastrointestinal tract: effect of loss of beta-catenin. Gastroenterology 126 : 1236–1246.
21. SauerB (1998) Inducible gene targeting in mice using the Cre/lox system. Methods 14 : 381–392.
22. BarkerN, van EsJH, KuipersJ, KujalaP, van den BornM, et al. (2007) Identification of stem cells in small intestine and colon by marker gene Lgr5. Nature 449 : 1003–1007.
23. Lopez-GarciaC, KleinAM, SimonsBD, WintonDJ (2010) Intestinal stem cell replacement follows a pattern of neutral drift. Science 330 : 822–825.
24. SnippertHJ, van der FlierLG, SatoT, van EsJH, van den BornM, et al. (2010) Intestinal crypt homeostasis results from neutral competition between symmetrically dividing Lgr5 stem cells. Cell 143 : 134–144.
25. ItzkovitzS, BlatIC, JacksT, CleversH, van OudenaardenA (2012) Optimality in the development of intestinal crypts. Cell 148 : 608–619.
26. QuynAJ, AppletonPL, CareyFA, SteeleRJ, BarkerN, et al. (2010) Spindle orientation bias in gut epithelial stem cell compartments is lost in precancerous tissue. Cell Stem Cell 6 : 175–181.
27. SternCD, FraserSE (2001) Tracing the lineage of tracing cell lineages. Nat Cell Biol 3: E216–218.
28. ReizelY, Chapal-IlaniN, AdarR, ItzkovitzS, ElbazJ, et al. (2011) Colon stem cell and crypt dynamics exposed by cell lineage reconstruction. PLoS Genet 7: e1002192.
29. BakerSM, PlugAW, ProllaTA, BronnerCE, HarrisAC, et al. (1996) Involvement of mouse Mlh1 in DNA mismatch repair and meiotic crossing over. Nat Genet 13 : 336–342.
30. Ewens WJ (2004) Mathematical Population Genetics. New York: Springer.
31. KingmanJFC (1982) The coalescent. Stochast Proc Appl 13 : 235–248.
32. KingmanJFC (1982) On the genealogy of large populations. J Appl Prob 19A: 27–43.
33. Wakeley J (2008) Coalescent Theory: An Introduction. Roberts & Company Publishers. 432 p.
34. FuYX (2006) Exact coalescent for the Wright-Fisher model. Theor Popul Biol 69 : 385–394.
35. FelsensteinJ (1981) Evolutionary trees from DNA sequences: a maximum likelihood approach. J Mol Evol 17 : 368–376.
36. MetropolisN, UlamS (1949) The Monte Carlo method. J Am Stat Assoc 44 : 335–341.
37. Efron B, Tibshirani RJ (1994) An Introduction to the Bootstrap. Chapman and Hall. 456 p.
38. de NavascuesJ, PerdigotoCN, BianY, SchneiderMH, BardinAJ, et al. (2012) Drosophila midgut homeostasis involves neutral competition between symmetrically dividing intestinal stem cells. EMBO J 31 : 2473–2485.
39. CaussinusE, GonzalezC (2005) Induction of tumor growth by altered stem-cell asymmetric division in Drosophila melanogaster. Nat Genet 37 : 1125–1129.
40. FloresI, CayuelaML, BlascoMA (2005) Effects of telomerase and telomere length on epidermal stem cell behavior. Science 309 : 1253–1256.
41. RandoTA (2006) Stem cells, ageing and the quest for immortality. Nature 441 : 1080–1086.
42. SatoT, van EsJH, SnippertHJ, StangeDE, VriesRG, et al. (2011) Paneth cells constitute the niche for Lgr5 stem cells in intestinal crypts. Nature 469 : 415–418.
43. ChakkalakalJV, JonesKM, BassonMA, BrackAS (2012) The aged niche disrupts muscle stem cell quiescence. Nature 490 : 355–360.
44. ConboyIM, ConboyMJ, WagersAJ, GirmaER, WeissmanIL, et al. (2005) Rejuvenation of aged progenitor cells by exposure to a young systemic environment. Nature 433 : 760–764.
45. MedzhitovR (2008) Origin and physiological roles of inflammation. Nature 454 : 428–435.
46. BuchonN, BroderickNA, ChakrabartiS, LemaitreB (2009) Invasive and indigenous microbiota impact intestinal stem cell activity through multiple pathways in Drosophila. Genes Dev 23 : 2333–2344.
47. CroninSJ, NehmeNT, LimmerS, LiegeoisS, PospisilikJA, et al. (2009) Genome-wide RNAi screen identifies genes involved in intestinal pathogenic bacterial infection. Science 325 : 340–343.
48. DingliD, TraulsenA, MichorF (2007) (A)symmetric stem cell replication and cancer. PLoS Comput Biol 3: e53.
49. WilliamsGC (1957) Pleiotropy, natural selection, and the evolution of senescence. Evolution 11 : 398–411.
50. CongdonKL, ReyaT (2008) Divide and conquer: how asymmetric division shapes cell fate in the hematopoietic system. Curr Opin Immunol 20 : 302–307.
51. WuM, KwonHY, RattisF, BlumJ, ZhaoC, et al. (2007) Imaging hematopoietic precursor division in real time. Cell Stem Cell 1 : 541–554.
52. SharplessNE, DePinhoRA (2007) How stem cells age and why this makes us grow old. Nat Rev Mol Cell Biol 8 : 703–713.
53. GotzM, HuttnerWB (2005) The cell biology of neurogenesis. Nat Rev Mol Cell Biol 6 : 777–788.
54. LechlerT, FuchsE (2005) Asymmetric cell divisions promote stratification and differentiation of mammalian skin. Nature 437 : 275–280.
55. PoulsonND, LechlerT (2010) Robust control of mitotic spindle orientation in the developing epidermis. J Cell Biol 191 : 915–922.
56. EmaH, TakanoH, SudoK, NakauchiH (2000) In vitro self-renewal division of hematopoietic stem cells. J Exp Med 192 : 1281–1288.
57. TakanoH, EmaH, SudoK, NakauchiH (2004) Asymmetric division and lineage commitment at the level of hematopoietic stem cells: inference from differentiation in daughter cell and granddaughter cell pairs. J Exp Med 199 : 295–302.
58. PennisiE (2012) The biology of genomes. Single-cell sequencing tackles basic and biomedical questions. Science 336 : 976–977.
59. ZongC, LuS, ChapmanAR, XieXS (2012) Genome-wide detection of single-nucleotide and copy-number variations of a single human cell. Science 338 : 1622–1626.
60. PottenCS, LoefflerM (1990) Stem cells: attributes, cycles, spirals, pitfalls and uncertainties. Lessons for and from the crypt. Development 110 : 1001–1020.
61. SchepersAG, SnippertHJ, StangeDE, van den BornM, van EsJH, et al. (2012) Lineage tracing reveals Lgr5+ stem cell activity in mouse intestinal adenomas. Science 337 : 730–735.
62. ChengH, BjerknesM (1985) Whole population cell kinetics and postnatal development of the mouse intestinal epithelium. Anat Rec 211 : 420–426.
63. DehmerJJ, GarrisonAP, SpeckKE, DekaneyCM, Van LandeghemL, et al. (2011) Expansion of intestinal epithelial stem cells during murine development. PLoS One 6: e27070.
64. Ross MS (2006) Simulation. Academic Press. 312 p.
65. YangZ (1994) Maximum likelihood phylogenetic estimation from DNA sequences with variable rates over sites: approximate methods. J Mol Evol 39 : 306–314.
66. SokalR, MichenerC (1958) A statistical method for evaluating systematic relationships. University of Kansas Science Bulletin 38 : 1409–1438.
67. PopescuAA, HuberKT, ParadisE (2012) ape 3.0: New tools for distance-based phylogenetics and evolutionary analysis in R. Bioinformatics 28 : 1536–1537.
Štítky
Genetika Reprodukční medicína
Článek MSH3 Polymorphisms and Protein Levels Affect CAG Repeat Instability in Huntington's Disease MiceČlánek Yemanuclein and HIRA Cooperate for Assembly of H3.3-Containing Nucleosomes in the Male Pronucleus
Článek vyšel v časopisePLOS Genetics
Nejčtenější tento týden
2013 Číslo 2- Souvislost haplotypu M2 genu pro annexin A5 s opakovanými reprodukčními ztrátami
- Akutní intermitentní porfyrie
- Primární hyperoxalurie – aktuální možnosti diagnostiky a léčby
- Jak zlepšit účinnost psychofarmakoterapie a adherenci k ní pomocí farmakogenetiky? – kazuistiky z české praxe
- Spolehlivost LH testů
-
Všechny články tohoto čísla
- Complex Inheritance of Melanoma and Pigmentation of Coat and Skin in Grey Horses
- A Meta-Analysis of Thyroid-Related Traits Reveals Novel Loci and Gender-Specific Differences in the Regulation of Thyroid Function
- Genetic Landscape of Open Chromatin in Yeast
- Deleterious Alleles in the Human Genome Are on Average Younger Than Neutral Alleles of the Same Frequency
- Age-Dependent Transition from Cell-Level to Population-Level Control in Murine Intestinal Homeostasis Revealed by Coalescence Analysis
- Next-Generation Sequencing Identifies the Danforth's Short Tail Mouse Mutation as a Retrotransposon Insertion Affecting Expression
- ImmunoChip Study Implicates Antigen Presentation to T Cells in Narcolepsy
- Massive Mitochondrial Gene Transfer in a Parasitic Flowering Plant Clade
- Comment on “Genomic Hypomethylation in the Human Germline Associates with Selective Structural Mutability in the Human Genome”
- The Prefoldin Bud27 Mediates the Assembly of the Eukaryotic RNA Polymerases in an Rpb5-Dependent Manner
- Genetic Determinants of Trabecular and Cortical Volumetric Bone Mineral Densities and Bone Microstructure
- Encodes a Novel and -Genus-Specific Regulator of Photoperiodic Flowering in Rice
- Only One Isoform of CTP Synthase Forms the Cytoophidium
- Mechanisms Involved in the Functional Divergence of Duplicated GroEL Chaperonins in DK1622
- A Genome-Wide RNAi Screen in Identifies the Nicotinic Acetylcholine Receptor Subunit ACR-7 as an Antipsychotic Drug Target
- Autophagy Induction Is a Tor- and Tp53-Independent Cell Survival Response in a Zebrafish Model of Disrupted Ribosome Biogenesis
- Ancient DNA Reveals Prehistoric Gene-Flow from Siberia in the Complex Human Population History of North East Europe
- Inflammation-Mediated Genetic and Epigenetic Alterations Drive Cancer Development in the Neighboring Epithelium upon Stromal Abrogation of TGF-β Signaling
- MicroRNA-3148 Modulates Allelic Expression of Toll-Like Receptor 7 Variant Associated with Systemic Lupus Erythematosus
- RNAi–Based Functional Profiling of Loci from Blood Lipid Genome-Wide Association Studies Identifies Genes with Cholesterol-Regulatory Function
- CELF Family RNA–Binding Protein UNC-75 Regulates Two Sets of Mutually Exclusive Exons of the Gene in Neuron-Specific Manners in
- Coordination of Chromatid Separation and Spindle Elongation by Antagonistic Activities of Mitotic and S-Phase CDKs
- The Ubiquitin Ligase Subunit Acts in Target Tissue to Restrict Tracheal Terminal Cell Branching and Hypoxic-Induced Gene Expression
- Mitotic Evolution of Shows a Stable Core Genome but Recombination in Antigen Families
- Tysnd1 Deficiency in Mice Interferes with the Peroxisomal Localization of PTS2 Enzymes, Causing Lipid Metabolic Abnormalities and Male Infertility
- A Regulatory Pathway, Ecdysone-Transcription Factor Relish-Cathepsin L, Is Involved in Insect Fat Body Dissociation
- PcG-Mediated Higher-Order Chromatin Structures Modulate Replication Programs at the BX-C
- MSH3 Polymorphisms and Protein Levels Affect CAG Repeat Instability in Huntington's Disease Mice
- JNK-Interacting Protein 3 Mediates the Retrograde Transport of Activated c-Jun N-Terminal Kinase and Lysosomes
- Discovery of a Splicing Regulator Required for Cell Cycle Progression
- Rearrangements of 2.5 Kilobases of Noncoding DNA from the Locus Define Predictive Rules of Genomic -Regulatory Logic
- Admixture Mapping in Lupus Identifies Multiple Functional Variants within IFIH1 Associated with Apoptosis, Inflammation, and Autoantibody Production
- Roles of the Developmental Regulator Homothorax in Limiting Longevity in
- miR-199a-5p Is Upregulated during Fibrogenic Response to Tissue Injury and Mediates TGFbeta-Induced Lung Fibroblast Activation by Targeting Caveolin-1
- A Kinome-Wide RNAi Screen in Glia Reveals That the RIO Kinases Mediate Cell Proliferation and Survival through TORC2-Akt Signaling in Glioblastoma
- Assembly of the Auditory Circuitry by a Genetic Network in the Mouse Brainstem
- SOX2 Co-Occupies Distal Enhancer Elements with Distinct POU Factors in ESCs and NPCs to Specify Cell State
- Retrotransposon Activates Ectopic Expression: A Short Tail
- Confounding by Repetitive Elements and CpG Islands Does Not Explain the Association between Hypomethylation and Genomic Instability
- Cell Reprogramming Requires Silencing of a Core Subset of Polycomb Targets
- Properties and Modeling of GWAS when Complex Disease Risk Is Due to Non-Complementing, Deleterious Mutations in Genes of Large Effect
- Essential Developmental, Genomic Stability, and Tumour Suppressor Functions of the Mouse Orthologue of
- Conditional Inactivation of the DNA Damage Response Gene in Mouse Testis Reveals Separable Roles for Components of the RAD9-RAD1-HUS1 Complex in Meiotic Chromosome Maintenance
- Genome-Wide Analysis Points to Roles for Extracellular Matrix Remodeling, the Visual Cycle, and Neuronal Development in Myopia
- Patterning of Leaf Vein Networks by Convergent Auxin Transport Pathways
- An Evolutionary Perspective on Epistasis and the Missing Heritability
- A Retrotransposon Insertion in the 5′ Regulatory Domain of Ptf1a Results in Ectopic Gene Expression and Multiple Congenital Defects in Danforth's Short Tail Mouse
- The Mub1/Ubr2 Ubiquitin Ligase Complex Regulates the Conserved Dsn1 Kinetochore Protein
- Mutations Can Cause Enamel-Renal Syndrome (ERS)
- Yemanuclein and HIRA Cooperate for Assembly of H3.3-Containing Nucleosomes in the Male Pronucleus
- Hepatocyte Growth Factor, a Determinant of Airspace Homeostasis in the Murine Lung
- ISWI and CHD Chromatin Remodelers Bind Promoters but Act in Gene Bodies
- COM-1 Promotes Homologous Recombination during Meiosis by Antagonizing Ku-Mediated Non-Homologous End Joining
- Control of Multicellular Development by the Physically Interacting Deneddylases DEN1/DenA and COP9 Signalosome
- Antagonism Versus Cooperativity with TALE Cofactors at the Base of the Functional Diversification of Hox Protein Function
- Dynamic Association of NUP98 with the Human Genome
- Ectopic Expression of Induces Spinal Defects, Urogenital Defects, and Anorectal Malformations in Mice
- Regulation of Contributes to the Lineage Potential of Neurogenin3+ Endocrine Precursor Cells in the Pancreas
- Gene-Based Testing of Interactions in Association Studies of Quantitative Traits
- The Amidation Step of Diphthamide Biosynthesis in Yeast Requires , a Gene Identified through Mining the - Interaction Network
- Plant-Symbiotic Fungi as Chemical Engineers: Multi-Genome Analysis of the Clavicipitaceae Reveals Dynamics of Alkaloid Loci
- Genome-Wide Diversity in the Levant Reveals Recent Structuring by Culture
- DNA Methylation Mediated Control of Gene Expression Is Critical for Development of Crown Gall Tumors
- Identification of the SlmA Active Site Responsible for Blocking Bacterial Cytokinetic Ring Assembly over the Chromosome
- Expression of a Novel P22 ORFan Gene Reveals the Phage Carrier State in Typhimurium
- Altered Cohesin Gene Dosage Affects Mammalian Meiotic Chromosome Structure and Behavior
- Quantitative Analysis of Histone Modifications: Formaldehyde Is a Source of Pathological N-Formyllysine That Is Refractory to Histone Deacetylases
- Duplicate Abalone Egg Coat Proteins Bind Sperm Lysin Similarly, but Evolve Oppositely, Consistent with Molecular Mimicry at Fertilization
- Lessons from on the Strengths and Weaknesses of Structured Association Mapping
- DNA–Methylome Analysis of Mouse Intestinal Adenoma Identifies a Tumour-Specific Signature That Is Partly Conserved in Human Colon Cancer
- Transposon Variants and Their Effects on Gene Expression in
- Polygenic Modeling with Bayesian Sparse Linear Mixed Models
- Single Transmembrane Peptide DinQ Modulates Membrane-Dependent Activities
- The JNK Signaling Pathway Activates Expression of Stress Response Genes by Derepressing the Fos/HDAC Repressor Complex
- The Interaction of CtIP and Nbs1 Connects CDK and ATM to Regulate HR–Mediated Double-Strand Break Repair
- Regulation of Metamorphosis by Xenobiotic Response Regulators
- PLOS Genetics
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Complex Inheritance of Melanoma and Pigmentation of Coat and Skin in Grey Horses
- Coordination of Chromatid Separation and Spindle Elongation by Antagonistic Activities of Mitotic and S-Phase CDKs
- Autophagy Induction Is a Tor- and Tp53-Independent Cell Survival Response in a Zebrafish Model of Disrupted Ribosome Biogenesis
- Assembly of the Auditory Circuitry by a Genetic Network in the Mouse Brainstem
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání






