-
Články
- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Fifteen Years Later: Hard and Soft Selection Sweeps Confirm a Large Population Number for HIV In Vivo
article has not abstract
Published in the journal: . PLoS Genet 10(2): e32767. doi:10.1371/journal.pgen.1004179
Category: Perspective
doi: https://doi.org/10.1371/journal.pgen.1004179Summary
article has not abstract
Even among RNA viruses, which generally exhibit high evolutionary plasticity due to low fidelity of their RNA polymerases, HIV-1 is second only to HCV for its ability to generate within-host genetic diversity [1]. HIV's rapid generation time leads to this high genetic diversity. The unfortunate consequences of HIV's rapid evolution are resistance to antiretroviral drugs [1], partial escape from immune responses [2]–[4], the ability to switch tropism for target cells [5], and potential threats to new therapeutic strategies [6], [7]. The forces driving and influencing HIV evolution include Darwinian selection, limited population size, linkage, recombination, epistasis, spatial aspects, and dynamic factors (particularly due to the immune response). These factors, and the parameters that define them, can be difficult to discern. One of the most elusive parameters critically important for the rate of evolution in every medically relevant scenario is the “effective population number” (Neff) (Figure 1). By definition, the census population size of HIV is the total number of infectious proviruses integrated into the cellular DNA of an individual at a given time. However, the genetically relevant Neff may differ substantially from the census population size. In this volume of PLOS Genetics, Pennings and colleagues [8] use new insights into “hard” and “soft” selective sweeps to estimate the effective population size of HIV.
Fig. 1. Beneficial viral mutants (red) arise in the “effective” virus subpopulation (Neff, pink circle) and spread gradually to the entire “census” population (blue circle). 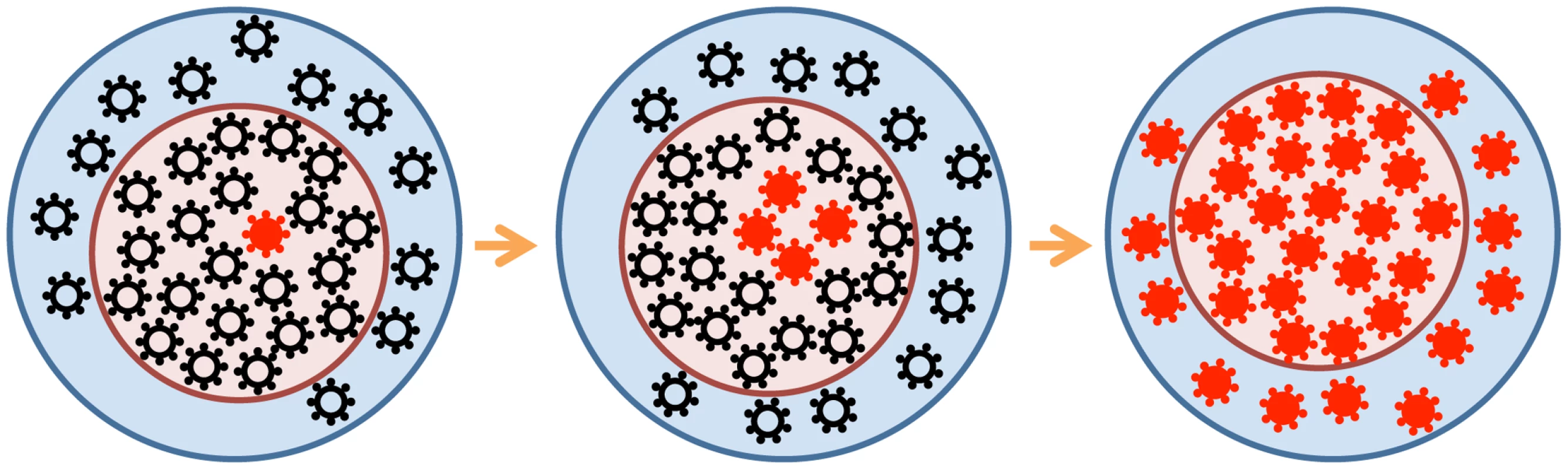
For a number of reasons (see the text), the effective population may be much smaller than the census population. The search for Neff (and other HIV evolutionary parameters) has gone on for almost two decades, following every turn and hitting each pothole on the eventful road of HIV modeling [9]. The rapidity of resistance to monotherapy (in 1–2 weeks) was explained by the deterministic selection of alleles that preexist therapy in minute quantities [1]. The large numbers of virus-producing cells (∼108) in the lymphoid tissue of experimentally infected macaques seemed to confirm this simple Darwinian selection model [10]. However, the Darwinian view has faced challenges. Tajima's “neutrality test” applied to HIV sequences in untreated patients assumed that selection was neutral and predicted much smaller “effective” populations, of Neff∼103 [11]. Since Tajima's approach was designed to detect isolated selective sweeps at one or a few mutant sites—while HIV exhibits hundreds of diverse sites in vivo—two groups re-tested the result. A linkage disequilibrium (LD) test [12] and analysis of the variation in the time to drug resistance [13] arrived at the same value, Neff = (5–10)×105, for an average patient (with the mutation rate ∼10−5 per base). Such populations are sufficiently large for deterministic selection to dominate, yet not large enough to neglect stochastic effects altogether. The LD test [12] is affected by recombination, and HIV's recombination rate had not been well measured at that time. The recent measurement of 5×10−6 crossovers per base per HIV replication cycle in an average untreated individual [14]–[16] updates Neff to (1–2)×105, not far from the original value. A recent study of the pattern of diversity accumulation in early and late HIV infection confirms the range of Neff [17]. However, all these estimates of Neff are lower bounds.
Pennings et al. [8] continue this quest for an effective population size of HIV using a new method based on a theoretical calculation of the probability of multiple introductions of a beneficial allele at a site before it is fixed in a population [18]. The prediction does not depend on whether mutations are new or result from standing variation prior to therapy. The authors use sequence data obtained from 30 patients who failed suboptimal antiretroviral regimens, including efavirenz [19]—a non-nucleoside reverse transcriptase (RT) inhibitor (NNRTI)—and who exhibited a rise of drug-resistant alleles in RT. The sequence data reveal fixation of two alleles, both corresponding to an amino-acid replacement K103N. Pennings et al.'s analysis focuses on the genetic composition at RT codon 103 and the adjacent 500 nucleotides. Based on the changes in the genetic diversity in this region, 30 fixations are classified into “hard” selective sweeps with a single parental sequence, or “soft” sweeps with multiple parental sequences. Observing that both types of sweep occurred at similar frequencies (also confirmed by observations in other resistance codons), the authors predict Neff = 1.5×105, in agreement with the LD test.
Pennings et al. also discuss why “selectively neutral” methods based on synonymous diversity underestimate the population size. It is well known that a selection sweep lowers the diversity at linked sites (hence the term “sweep”) and any method assuming selective neutrality translates lower diversity to smaller Neff. The interesting part is the dynamic component of this effect. Pennings et al. demonstrate that rapid sweeps are followed by long periods when the diversity recovers at the linked sites (for synonymous sites, these periods are very long). From another angle, we can add that selection shortens the time to the common ancestor, which decreases the sequence divergence. The ancestral-tree argument is rather general and also applies to a large number of linked sites evolving under selection [20]–[23].
The previous estimates [12], [13], [17] were lower bounds on Neff. In contrast, the Pennings et al. study puts a number on Neff. However, this number (Neff = 1.5×105) raises a question: why is Neff so far below the census population size of 108 or more? Pennings et al. offer an elegant explanation of this relatively small Neff in the spirit of the “traveling wave” approach [24]–[27]. They note that resistant alleles at different sites emerge against different fitness backgrounds. To be fixed, alleles conferring a small benefit must emerge in the most-fit genomes [28], [29]; hence, the effective Neff for these alleles is small. Alleles with a larger beneficial effect can explore a larger fraction of population (larger Neff). Conceptually, this idea is quite correct; quantitatively, in the context of drug resistance, some problems arise. For example, the fitness benefit from a resistance mutation (under drug) is almost 100%, while the difference between the fittest and the average genome (in untreated patients) is a modest ∼10% [14]. Indeed, the average selection coefficient is quite small, ∼0.5% [14], [15].
There may be several other reasons for Neff<108, as follows.
-
By considering only 500 bases (∼5%) of the HIV genome, the study may underestimate the number of genetic backgrounds in which the resistant allele can be observed.
-
Neff is likely to vary in time—similar to viremia, which decays strongly after the onset of therapy and rebounds after its failure—and the placement of the inferred population size within the therapy time frame is unclear. Specifically, it is unclear from the empirical source [19] whether K103N mutations are generated before therapy (which is likely, considering that the mutation of interest decays very slowly in vivo in untreated patients and therefore has a low mutation cost [30]) or after therapy fails for another reason (see Figure 1 in [19]). In the first scenario, inferred Neff = 105 is the pretreatment number. In the second scenario, the pretreatment number must be much higher than 105, since the replicating census population is reduced by a large factor (∼100) following initiation of therapy.
-
Other factors, such as variation of the population number among patients and the spatial organization of the infected tissue [31] (both neglected in the test), may be relevant. Furthermore, the authors' calculations rely on the assumption of equal mutation rates for the two resistance mutations analyzed (both transversions). If the underlying rate of AAA to AAC is much greater than that of to AAT, the cited analysis would have underestimated the frequency of soft sweeps, yielding an underestimate of Neff.
-
A significant complicating factor is the presence, in the parent study [19], of other drugs, particularly the nucleoside RT inhibitors (NRTIs) AZT and 3TC. In some cases, mutations conferring resistance to these drugs may have also contributed to failure (e.g., during the precursor monotherapy; see Figure 1 in [19]), and the requirement for these additional changes would have made the frequency of resistant strains much less than the estimate. For virus that escaped the combination treatment in the absence of NRTI mutations, replication was most likely occurring only in a fraction, or “sanctuary,” of cells that did not receive an inhibitory dose of these drugs. Either or both of these effects would have led to a potentially large underestimate of Neff. Indeed, a recent study of rapid NNRTI resistance, in SIV-infected monkeys treated with efavirenz monotherapy, used an ultrasensitive PCR assay to estimate the pre-therapy level of either K103N mutation as less than 0.0001% [32], implying a total replicating population of >106.
For these reasons, the value Neff = 1.5×105 obtained in the study of Pennings et al. should probably still be regarded as a lower bound. At the same time, the study solidifies our understanding of HIV evolution as a Darwinian process and leads to important questions regarding the structure of HIV population, which are still waiting for new insights.
Zdroje
1. CoffinJM (1995) HIV population dynamics in vivo: implications for genetic variation, pathogenesis, and therapy. Science 267 : 483–488.
2. GanusovVV, GoonetillekeN, LiuMK, FerrariG, ShawGM, et al. (2011) Fitness costs and diversity of the cytotoxic T lymphocyte (CTL) response determine the rate of CTL escape during acute and chronic phases of HIV infection. J Virol 85 : 10518–10528.
3. LiuY, McNevinJP, HolteS, McElrathMJ, MullinsJI (2011) Dynamics of viral evolution and CTL responses in HIV-1 infection. PLOS One 6: e15639 doi:10.1371/journal.pone.0015639
4. GoonetillekeN, LiuMK, Salazar-GonzalezJF, FerrariG, GiorgiE, et al. (2009) The first T cell response to transmitted/founder virus contributes to the control of acute viremia in HIV-1 infection. J Exp Med 206 : 1253–1272.
5. CoakleyE, PetropoulosCJ, WhitcombJM (2005) Assessing chemokine co-receptor usage in HIV. Curr Opin Infect Dis 18 : 9–15.
6. RouzineIM, WeinbergerLS (2013) Design requirements for interfering particles to maintain co-adaptive stability with HIV-1. J Virol 87 : 2081–2093.
7. MetzgerVT, Lloyd-SmithJO, WeinbergerLS (2011) Autonomous targeting of infectious superspreaders using engineered transmissible therapies. PLOS Comput Biol 7: e1002015 doi:10.1371/journal.pcbi.1002015
8. PenningsPS, KryazhimskyS, WakeleyJ (2014) Loss and recovery of genetic diversity in adapting populations of HIV. PLOS Genet 10: e1004000 doi:10.1371/journal.pgen.1004000
9. RouzineIM, WeinbergerL (2013) The quantitative theory of within-host viral evolution [review]. J Stat Mech P01009.
10. HaaseAT (1999) Population biology of HIV-1 infection: viral and CD4+ T cell demographics and dynamics in lymphatic tissues. Annu Rev Immunol 17 : 625–656.
11. Leigh-BrownAJ (1997) Analysis of HIV-1 env gene sequences reveals evidence for a low effective number in the viral population. Proc Natl Acad Sci U S A 94 : 1862–1865.
12. RouzineIM, CoffinJM (1999) Linkage disequilibrium test implies a large effective population number for HIV in vivo. Proc Natl Acad Sci U S A 96 : 10758–10763.
13. FrostSD, NijhuisM, SchuurmanR, BoucherCA, BrownAJ (2000) Evolution of lamivudine resistance in human immunodeficiency virus type 1-infected individuals: the relative roles of drift and selection. J Virol 74 : 6262–6268.
14. BatorskyR, KearneyMF, PalmerSE, MaldarelliF, RouzineIM, et al. (2011) Estimate of effective recombination rate and average selection coefficient for HIV in chronic infection. Proc Natl Acad Sci U S A 108 : 5661–5666.
15. NeherRA, LeitnerT (2010) Recombination rate and selection strength in HIV intra-patient evolution. PLOS Comput Biol 6: e1000660 doi:10.1371/journal.pcbi.1000660
16. JosefssonL, KingMS, MakitaloB, BrannstromJ, ShaoW, et al. (2011) Majority of CD4+ T cells from peripheral blood of HIV-1-infected individuals contain only one HIV DNA molecule. Proc Natl Acad Sci U S A 108 : 11199–11204.
17. MaldarelliF, KearneyM, PalmerS, StephensR, MicanJ, et al. (2013) HIV populations are large and accumulate high genetic diversity in a nonlinear fashion. J Virol 87 : 10313–10323.
18. PenningsPS, HermissonJ (2006) Soft sweeps II–molecular population genetics of adaptation from recurrent mutation or migration. Mol Biol Evol 23 : 1076–1084.
19. BachelerLT, AntonED, KudishP, BakerD, BunvilleJ, et al. (2000) Human immunodeficiency virus type 1 mutations selected in patients failing efavirenz combination therapy. Antimicrob Agents Chemother 44 : 2475–2484.
20. BrunetE, DerridaB, MuellerAH, MunierS (2007) Effect of selection on ancestry: An exactly soluble case and its phenomenological generalization. Phys Rev E Stat Nonlin Soft Mattter Phys 76 : 041104–041101.
21. SegerJ, SmithWA, PerryJJ, HunnJ, KaliszewskaZA, et al. (2010) Gene genealogies strongly distorted by weakly interfering mutations in constant environments. Genetics 184 : 529–545.
22. RouzineIM, CoffinJM (2010) Multi-site adaptation in the presence of infrequent recombination. Theor Popul Biol 77 : 189–204.
23. NeherRA, HallatschekO (2013) Genealogies of rapidly adapting populations. Proc Natl Acad Sci U S A 110 : 437–442.
24. TsimringLS, LevineH, KesslerD (1996) RNA virus evolution via a fitness-space model. Phys Rev Lett 76 : 4440–4443.
25. RouzineI, WakeleyJ, CoffinJ (2003) The solitary wave of asexual evolution. Proc Natl Acad Sci U S A 100 : 587–592.
26. DesaiMM, FisherDS (2007) Beneficial mutation selection balance and the effect of linkage on positive selection. Genetics 176 : 1759–1798.
27. HallatschekO (2010) The noisy edge of traveling waves. Proc Natl Acad Sci U S A 108 : 1783–1787.
28. NeherRA, ShraimanBI, FisherDS (2010) Rate of adaptation in large sexual populations. Genetics 184 : 467–481.
29. GoodBH, RouzineIM, BalickDJ, HallatschekO, DesaiMM (2012) Distribution of fixed beneficial mutations and the rate of adaptation in asexual populations. Proc Natl Acad Sci U S A 109 : 4950–4955.
30. PalmerS, BoltzV, MartinsonN, MaldarelliF, GrayG, et al. (2006) Persistence of nevirapine-resistant HIV-1 in women after single-dose nevirapine therapy for prevention of maternal-to-fetal HIV-1 transmission. Proc Natl Acad Sci U S A 103 : 7094–7099.
31. FrostSD, DumaurierMJ, Wain-HobsonS, BrownAJ (2001) Genetic drift and within-host metapopulation dynamics of HIV-1 infection. Proc Natl Acad Sci U S A 98 : 6975–6980.
32. BoltzVF, AmbroseZ, KearneyMF, ShaoW, KewalramaniVN, et al. (2012) Ultrasensitive allele-specific PCR reveals rare preexisting drug-resistant variants and a large replicating virus population in macaques infected with a simian immunodeficiency virus containing human immunodeficiency virus reverse transcriptase. J Virol 86 : 12525–12530.
Štítky
Genetika Reprodukční medicína
Článek Natural Polymorphisms in Influence Negative Selection and CD4∶CD8 Lineage Commitment in the RatČlánek MicroRNAs Located in the Hox Gene Clusters Are Implicated in Huntington's Disease PathogenesisČlánek Comparative RNAi Screens in and Reveal the Impact of Developmental System Drift on Gene FunctionČlánek Mutation of SLC35D3 Causes Metabolic Syndrome by Impairing Dopamine Signaling in Striatal D1 Neurons
Článek vyšel v časopisePLOS Genetics
Nejčtenější tento týden
2014 Číslo 2- Souvislost haplotypu M2 genu pro annexin A5 s opakovanými reprodukčními ztrátami
- Akutní intermitentní porfyrie
- Primární hyperoxalurie – aktuální možnosti diagnostiky a léčby
- Transthyretinová amyloidóza z pohledu neurologa a kardiologa aneb jak se vyhnout „misdiagnostice“?
- Jak zlepšit účinnost psychofarmakoterapie a adherenci k ní pomocí farmakogenetiky? – kazuistiky z české praxe
-
Všechny články tohoto čísla
- Fifteen Years Later: Hard and Soft Selection Sweeps Confirm a Large Population Number for HIV In Vivo
- The Same but Different: Worms Reveal the Pervasiveness of Developmental System Drift
- Serine Carboxypeptidase SCPEP1 and Cathepsin A Play Complementary Roles in Regulation of Vasoconstriction via Inactivation of Endothelin-1
- Coherent Functional Modules Improve Transcription Factor Target Identification, Cooperativity Prediction, and Disease Association
- A Long-Chain Flavodoxin Protects from Oxidative Stress and Host Bacterial Clearance
- Mammalian E-type Cyclins Control Chromosome Pairing, Telomere Stability and CDK2 Localization in Male Meiosis
- Influenza Virus Drug Resistance: A Time-Sampled Population Genetics Perspective
- Transcriptome-Wide Analyses of 5′-Ends in RNase J Mutants of a Gram-Positive Pathogen Reveal a Role in RNA Maturation, Regulation and Degradation
- Selective Disruption of Aurora C Kinase Reveals Distinct Functions from Aurora B Kinase during Meiosis in Mouse Oocytes
- X Chromosome Control of Meiotic Chromosome Synapsis in Mouse Inter-Subspecific Hybrids
- A Cohesin-Independent Role for NIPBL at Promoters Provides Insights in CdLS
- Extreme Population Differences in the Human Zinc Transporter ZIP4 (SLC39A4) Are Explained by Positive Selection in Sub-Saharan Africa
- Classic Selective Sweeps Revealed by Massive Sequencing in Cattle
- Genomic Networks of Hybrid Sterility
- Natural Polymorphisms in Influence Negative Selection and CD4∶CD8 Lineage Commitment in the Rat
- Oxidative Stress Is Not a Major Contributor to Somatic Mitochondrial DNA Mutations
- Molecular Identification of Collagen 17a1 as a Major Genetic Modifier of Laminin Gamma 2 Mutation-Induced Junctional Epidermolysis Bullosa in Mice
- Uncoupling of Molecular Maturation from Peripheral Target Innervation in Nociceptors Expressing a Chimeric TrkA/TrkC Receptor
- MicroRNAs Located in the Hox Gene Clusters Are Implicated in Huntington's Disease Pathogenesis
- Loss of Trabid, a New Negative Regulator of the Immune-Deficiency Pathway at the Level of TAK1, Reduces Life Span
- Targeted Ablation of Nesprin 1 and Nesprin 2 from Murine Myocardium Results in Cardiomyopathy, Altered Nuclear Morphology and Inhibition of the Biomechanical Gene Response
- Identification of Novel Genetic Loci Associated with Thyroid Peroxidase Antibodies and Clinical Thyroid Disease
- CEP-1, the p53 Homolog, Mediates Opposing Longevity Outcomes in Mitochondrial Electron Transport Chain Mutants
- Transcriptomics and Functional Genomics of ROS-Induced Cell Death Regulation by
- Quantitative Genome-Wide Genetic Interaction Screens Reveal Global Epistatic Relationships of Protein Complexes in
- Cascades of Genetic Instability Resulting from Compromised Break-Induced Replication
- Serine- and Threonine/Valine-Dependent Activation of PDK and Tor Orthologs Converge on Sch9 to Promote Aging
- Zfp322a Regulates Mouse ES Cell Pluripotency and Enhances Reprogramming Efficiency
- Insertional Mutagenesis and Deep Profiling Reveals Gene Hierarchies and a -Dependent Bottleneck in Lymphomagenesis
- DAAM Is Required for Thin Filament Formation and Sarcomerogenesis during Muscle Development in Drosophila
- Plasma Cholesterol–Induced Lesion Networks Activated before Regression of Early, Mature, and Advanced Atherosclerosis
- High-Resolution Profiling of Stationary-Phase Survival Reveals Yeast Longevity Factors and Their Genetic Interactions
- Comparative RNAi Screens in and Reveal the Impact of Developmental System Drift on Gene Function
- Accurate and Robust Genomic Prediction of Celiac Disease Using Statistical Learning
- Sex-Specific Embryonic Gene Expression in Species with Newly Evolved Sex Chromosomes
- Chromosome X-Wide Association Study Identifies Loci for Fasting Insulin and Height and Evidence for Incomplete Dosage Compensation
- Negative Feedback and Transcriptional Overshooting in a Regulatory Network for Horizontal Gene Transfer
- DNA Sequence Explains Seemingly Disordered Methylation Levels in Partially Methylated Domains of Mammalian Genomes
- Insights into the Genomic Landscape: Comparative Genomics Reveals Variations in Ploidy and Nutrient Utilisation Potential amongst Wine Isolates
- Molecular Evidence for the Inverse Comorbidity between Central Nervous System Disorders and Cancers Detected by Transcriptomic Meta-analyses
- The Centriolar Satellite Protein AZI1 Interacts with BBS4 and Regulates Ciliary Trafficking of the BBSome
- Fine-Mapping the Region Detects Common Variants Tagging a Rare Coding Allele: Evidence for Synthetic Association in Prostate Cancer
- Transmission Distortion Affecting Human Noncrossover but Not Crossover Recombination: A Hidden Source of Meiotic Drive
- A Variant in the Neuropeptide Receptor is a Major Determinant of Growth and Physiology
- Mutation of SLC35D3 Causes Metabolic Syndrome by Impairing Dopamine Signaling in Striatal D1 Neurons
- NSUN4 Is a Dual Function Mitochondrial Protein Required for Both Methylation of 12S rRNA and Coordination of Mitoribosomal Assembly
- MicroRNA-133 Inhibits Behavioral Aggregation by Controlling Dopamine Synthesis in Locusts
- Convergence of Light and ABA Signaling on the Promoter
- Arf4 Is Required for Mammalian Development but Dispensable for Ciliary Assembly
- Distinct Requirements for Cranial Ectoderm and Mesenchyme-Derived Wnts in Specification and Differentiation of Osteoblast and Dermal Progenitors
- Chk2 and P53 Regulate the Transmission of Healed Chromosomes in the Male Germline
- Ddc2 Mediates Mec1 Activation through a Ddc1- or Dpb11-Independent Mechanism
- Mapping the Fitness Landscape of Gene Expression Uncovers the Cause of Antagonism and Sign Epistasis between Adaptive Mutations
- Euchromatic Transposon Insertions Trigger Production of Novel Pi- and Endo-siRNAs at the Target Sites in the Germline
- miR-100 Induces Epithelial-Mesenchymal Transition but Suppresses Tumorigenesis, Migration and Invasion
- Canine Hereditary Ataxia in Old English Sheepdogs and Gordon Setters Is Associated with a Defect in the Autophagy Gene Encoding
- Within-Host Spatiotemporal Dynamics of Plant Virus Infection at the Cellular Level
- Analysis of Meiosis in SUN1 Deficient Mice Reveals a Distinct Role of SUN2 in Mammalian Meiotic LINC Complex Formation and Function
- Genome-Wide Association Study of Metabolic Traits Reveals Novel Gene-Metabolite-Disease Links
- Mechanistically Distinct Mouse Models for -Associated Retinopathy
- DAF-16/FoxO Directly Regulates an Atypical AMP-Activated Protein Kinase Gamma Isoform to Mediate the Effects of Insulin/IGF-1 Signaling on Aging in
- Chromosome I Controls Chromosome II Replication in
- Integrated Genomic Characterization Reveals Novel, Therapeutically Relevant Drug Targets in FGFR and EGFR Pathways in Sporadic Intrahepatic Cholangiocarcinoma
- The Iodotyrosine Deiodinase Ortholog SUP-18 Functions through a Conserved Channel SC-Box to Regulate the Muscle Two-Pore Domain Potassium Channel SUP-9
- The Genome of Highlights a Fish Pathogen Adapted to Fluctuating Environments
- Distinct DNA Binding Sites Contribute to the TCF Transcriptional Switch in and
- The Streamlined Genome of spp. Relative to Human Pathogenic Kinetoplastids Reveals a Parasite Tailored for Plants
- PLOS Genetics
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Genome-Wide Association Study of Metabolic Traits Reveals Novel Gene-Metabolite-Disease Links
- A Cohesin-Independent Role for NIPBL at Promoters Provides Insights in CdLS
- Classic Selective Sweeps Revealed by Massive Sequencing in Cattle
- Arf4 Is Required for Mammalian Development but Dispensable for Ciliary Assembly
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání



