-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaNegative Feedback and Transcriptional Overshooting in a Regulatory Network for Horizontal Gene Transfer
Horizontal gene transfer (HGT) is a major force driving bacterial evolution. Because of their ability to cross inter-species barriers, bacterial plasmids are essential agents for HGT. This ability, however, poses specific requisites on plasmid physiology, in particular the need to overcome a multilevel selection process with opposing demands. We analyzed the transcriptional network of plasmid R388, one of the most promiscuous plasmids in Proteobacteria. Transcriptional analysis by fluorescence expression profiling and quantitative PCR revealed a regulatory network controlled by six transcriptional repressors. The regulatory network relied on strong promoters, which were tightly repressed in negative feedback loops. Computational simulations and theoretical analysis indicated that this architecture would show a transcriptional burst after plasmid conjugation, linking the magnitude of the feedback gain with the intensity of the transcriptional burst. Experimental analysis showed that transcriptional overshooting occurred when the plasmid invaded a new population of susceptible cells. We propose that transcriptional overshooting allows genome rebooting after horizontal gene transfer, and might have an adaptive role in overcoming the opposing demands of multilevel selection.
Published in the journal: . PLoS Genet 10(2): e32767. doi:10.1371/journal.pgen.1004171
Category: Research Article
doi: https://doi.org/10.1371/journal.pgen.1004171Summary
Horizontal gene transfer (HGT) is a major force driving bacterial evolution. Because of their ability to cross inter-species barriers, bacterial plasmids are essential agents for HGT. This ability, however, poses specific requisites on plasmid physiology, in particular the need to overcome a multilevel selection process with opposing demands. We analyzed the transcriptional network of plasmid R388, one of the most promiscuous plasmids in Proteobacteria. Transcriptional analysis by fluorescence expression profiling and quantitative PCR revealed a regulatory network controlled by six transcriptional repressors. The regulatory network relied on strong promoters, which were tightly repressed in negative feedback loops. Computational simulations and theoretical analysis indicated that this architecture would show a transcriptional burst after plasmid conjugation, linking the magnitude of the feedback gain with the intensity of the transcriptional burst. Experimental analysis showed that transcriptional overshooting occurred when the plasmid invaded a new population of susceptible cells. We propose that transcriptional overshooting allows genome rebooting after horizontal gene transfer, and might have an adaptive role in overcoming the opposing demands of multilevel selection.
Introduction
Horizontal gene transfer (HGT) is ubiquitous in bacteria. Because its important role in bacterial adaptation, HGT has been traditionally compared to sexual reproduction in higher eukaryotes. In bacteria, however, HGT is not mediated by specific intracellular mechanisms, but it is the byproduct of the pervasive movement of a myriad of mobile genetic elements. These include transposons, phages, ICEs and, most notably, plasmids [1]. Among them, broad host range (BHR) plasmids of Proteobacteria stand out because of their ability to colonize a wide range of bacterial species. This ability makes BHR plasmids efficient shuttles for HGT, clearly illustrated in the last decades by their leading role in the spread of antibiotic resistance genes among microbial populations [2].
Bacterial plasmids are agents for HGT, but they themselves are genetic replicons with their own, idiosyncratic, evolutionary history [3], [4]. Plasmid fitness depends on two basic physiological functions: maintenance within the bacterial host and transfer into new hosts; functions that are encoded in the plasmid genome. However, since plasmids can only exist inside a bacterial cell, their fitness is also host dependent. Plasmids impose a burden on host fitness [5], [6], [7], [8], which is dependent on the collective effect of the plasmid population within a given cell. The overall fitness of a plasmid replicon therefore depends not only on its own phenotype, but also on the phenotype of other co-residing plasmid copies. This dependency on the group phenotype puts plasmids under multilevel selection [9]. Multilevel selection forces plasmids to confront a paradoxical situation. Competition between plasmid copies within a given cell favors plasmids with higher copy number, superior partition systems and higher transfer rates [9]. However, these processes come to a cost, since plasmid consumption of resources imposes a metabolic burden that hampers host fitness. Competition between plasmid-containing cells, on the contrary, selects for plasmids that minimize the burden imposed onto the host. Both selection levels are thus intrinsically in conflict, and an adequate regulation of gene expression becomes essential to ensure plasmid survival [10].
Transcriptional regulation is common in plasmids, and virtually all functions in plasmid physiology have been found to be under transcriptional control [11]. In some cases, this control is exerted in sophisticated and apparently redundant layers. For example, plasmid R1 replication is controlled simultaneously by an antisense RNA and a transcriptional repressor [12] [13]. In other cases, like in the broad host range plasmid RP4, transcriptional regulation is organized under a global network that coordinates all functions in the plasmid's physiology [14]. Unfortunately, despite our knowledge of the molecular biology of transcriptional regulation, our understanding of the signals that plasmid regulatory circuits respond to is scarce. Plasmids from Gram+ bacteria regulate conjugation according to external cues about the abundance of possible receptors. These cues are communicated in the form of specific pheromones [15]. Such systems are generally not found in plasmids from Proteobacteria, with the remarkable exception of Ti-like plasmids from Alpha-Proteobacteria, which monitor external conditions via a quorum sensing mechanism[16] [17]. Apart from these and a few other cases, the input information that plasmid regulatory circuits monitor remains elusive.
Trying to understand the fundamental principles of plasmid transcriptional control, we analyzed the regulatory network of plasmid R388. Plasmid R388 is the smallest BHR conjugative plasmid found in Proteobacteria [3]. It shows an extensive host range, which overlaps with that of plasmid RP4, another model BHR plasmid [18]. Remarkably, plasmid RP4 is phylogenetically unrelated to plasmid R388 [3]. This situation allowed us to compare two plasmid networks that evolved independently, but under similar selective constraints. Using fluorescence expression profiling and quantitative PCR, we found a global regulatory network that controlled plasmid R388 transcription. Unlike the archetypical plasmids from Gram+ bacteria or Ti-like plasmids, the network seemed to be unresponsive to environmental changes, or quorum signals. The network was based on a basic regulatory motif: a strong promoter controlled by a tight negative feedback loop (NFL). We show, computationally and experimentally, that this architecture induces transcriptional overshooting after horizontal transfer of the plasmid.
Results
Intergenic regions in plasmid R388 DNA were PCR-amplified and cloned in the low copy number reporter vector pUA66 [19] to drive transcription of gfpmut2 after a strong ribosomal binding site. Out of the 19 intergenic regions cloned, 15 showed transcriptional activities at least two-fold higher than the promoter-less vector, and were considered to contain a promoter (Figure 1). To compare the transcriptional strength of these promoters against a known standard, the activity of ParaBAD was measured at different arabinose concentrations. ParaBAD promoter reached 105 GFP/OD units at maximal induction, and 13 out of 15 R388 promoters showed levels similar to this value (Figure 1, Supporting Table S1). Therefore R388 promoters, when assayed in the absence of the plasmid network, have strong transcriptional activities.
Fig. 1. Promoters in plasmid R388. 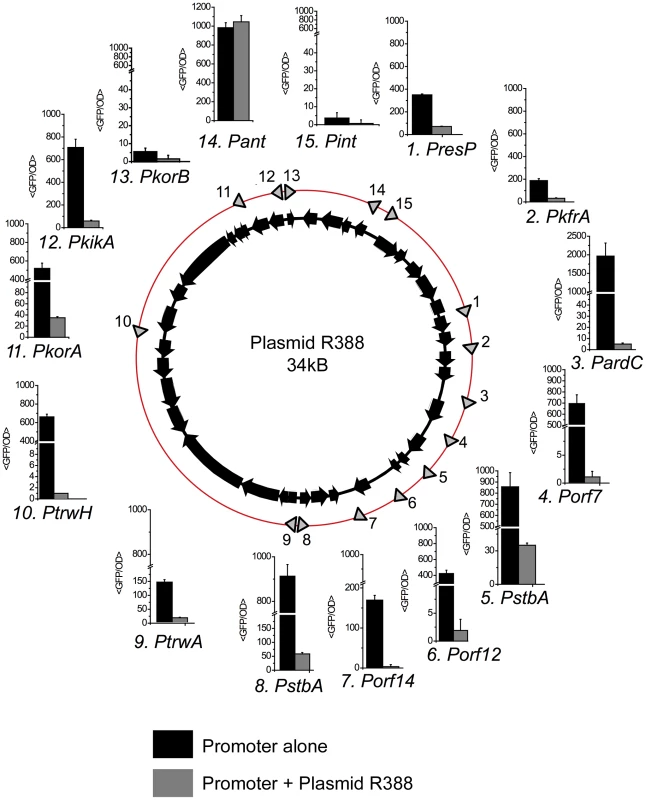
The figure shows the location and transcriptional activity of promoters detected in plasmid R388 genome. The location of each promoter is indicated by an arrow on the red circle. Each promoter receives the name of the first gene encoded in the transcriptional unit. Bar charts indicate the expression levels when the promoter activity was measured alone (black columns) or in cells that also contained plasmid R388 (grey columns). The expression levels (<GFP/OD>) represent the average GFP/OD (×102) level achieved by cells growing in exponential phase. Each column represents the average and standard deviation of at least five independent experiments. Transcriptional activity decreased sharply when the promoters were assayed in cells that also contained plasmid R388 (Figure 1, Supporting Table S1). The repression fold exerted by the plasmid ranged from 5 (PresP) to more than 500 fold (Porf7). Six promoters (PardC, Porf14, Porf12, PkorB, PtrwH, Porf7) dropped to levels close to background, and another six (PresP, PkfrA, PssB, PstbA, PkorA, PkikA) showed values similar to those of repressed PlacZ (1*103 GFP/OD). The only promoters that showed no changes in the presence of plasmid R388 were Pint and Pant. Interestingly, these promoters do not belong to the plasmid backbone: they are part of the In-3 integron platform, which incorporated recently, in evolutionary terms, into the plasmid genetic structure [20]. Therefore, when the full regulatory network was present, all promoters from the plasmid backbone were repressed, and kept at levels lower or similar to LacI-repressed PlacZ.
To determine the transcriptional units of the plasmid, mRNA levels during exponential growth were analysed by RT-qPCR. Relative mRNA abundance was measured using a set of 66 primer pairs, designed to cover the entire plasmid genome. From these 66 primer pairs, 60 showed efficiencies in the interval 0.9<E<1.2 (Figure 2A, left upper panel) and were considered suitable for quantification. mRNA was extracted from cells growing in rich media at mid-exponential phase, and retrotranscribed into cDNA as described in Materials and Methods. Using 300 ng total RNA, we obtained an average threshold cycle (Ct) of 19.9 with cv = 0.12. Results for each primer pair were normalized measuring the Ct corresponding to 5 ng of purified plasmid DNA. Results (Figure 2A, left lower panel), showed a tight distribution with an average Ct of 14.2 and cv = 0.034. Relative abundances of mRNAs were expressed as ΔCt = CtcDNA-CtDNA [21] and a representation of the average ΔCt obtained for each primer pair in three independent experiments is shown in figure 2B. Known untranscribed regions, like the plasmid origin of transfer (between PstbA and PtrwA), yielded ΔCt = −8, while the most actively transcribed region corresponded to the integron cassettes, with ΔCt = 2. Overall, the transcriptional profile clearly delimitated the boundaries between transcriptional units (Figure 2.B). A comparison between promoter strengths, determined by fluorescence profiling, and mRNA abundances, measured by RT-qPCR (figure 2A, left lower panel), showed that both measurements were not linearly correlated (r2 = 0.49), indicating that mRNA processing and degradation also played significant roles in determining plasmid levels of expression.
Fig. 2. Transcriptional units in plasmid R388. 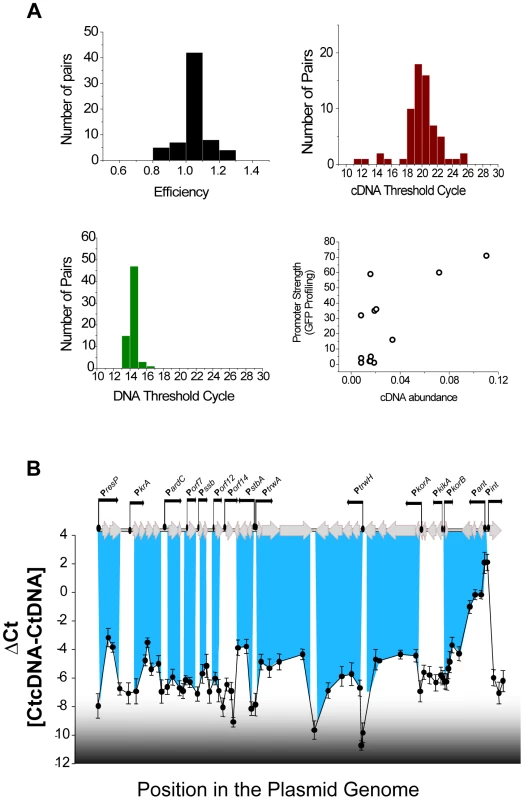
(A) Statistics of the 66 primer pairs used to measure transcriptional levels in plasmid R388 (Upper right) Histogram showing the efficiency (calculated as indicated in materials and methods) of the primer pairs. (Upper right) Histogram showing the Ct obtained in qPCR amplifications from plasmid cDNA. (Lower left) Histogram showing the Ct obtained in qPCR amplifications from purified plasmid DNA. (Lower right) Scatter plot showing the relationship between the promoter activity (obtained from figure 1, in GFP/OD unit on the y axis) and the mRNA levels measured by RT-qPCR (ΔCt, x axis). (B) Transcriptional landscape of plasmid R388. The graph shows the relative abundance of mRNA, indicated as ΔCt = CtcDNA-CtDNA) along the plasmid genome. Each unit in the y axis corresponds to a 2 fold increase in mRNA. Peaks correspond to highly transcribed regions and valleys correspond to non-transcribed regions. The highlighted blue lines indicate the overlapping of the transcriptional units and the plasmid promoters identified in figure 1. To determine the topology of the plasmid regulatory network, we tried to ascribe each plasmid promoter to its cognate regulators. ORFs from the plasmid genome that were either orphan, or showed homology to known transcriptional regulators, were considered potential candidates to encode a plasmid regulator. These ORFs were cloned in expression vector pBAD33, and the transcriptional activity of plasmid promoters was measured in the presence of all putative regulators. Expression profiles are shown in supporting figures S1 and S2, and steady-state levels are indicated in Supporting Table S1. Results allowed the identification of six plasmid proteins (ResP, KfrA, ArdK, StbA, TrwA and KorA) able to repress at least one of the plasmid promoters. (Supporting Table S1 and Supporting figure S1). Among the regulators identified, we did not find any transcriptional activator. All regulators were repressors involved in negative feedback loops (Figure 3A). Three of them controlled only their own promoter, thus constituting simple negative feedback loops (ResP, KfrA and TrwA). Another three (ArdK, StbA and KorA) controlled more complicated circuits. Protein ArdK repressed expression from PardC, Porf7, Porf12, Porf14 and Pssb, its own promoter (Supporting fig. S1). All these promoters direct the transcription of genes involved in the stable maintenance of the plasmid [3]. Therefore, ArdK seems to regulate the vegetative maintenance of plasmid R388. Similarly, protein KorA was found to regulate PtrwH, PkorA, PkikA, PkorB and its own promoter, PkorA (Supporting Fig. S2). All these promoters are responsible for expression of the Type IV secretion system, involved in plasmid conjugation. Therefore, KorA acted as the main transcriptional regulator for expression of the conjugative pilus. The third protein involved in a complex regulatory circuit was StbA. Gene stbA is part of an operon responsible for plasmid segregation [22] and was found to decrease PstbA transcription 50-fold (Figure 3A, Supporting Table S1). StbA also repressed transcription from promoters PardC, Porf7, Porf12 and Porf14; indicating that its target repertoire overlaps with that of ArdK (Supporting Fig. S1). Similarly, StbA repressed the promoters targeted by KorA, although the level of repression exerted was significantly lower (2 to 10-fold decrease compared to the 90-fold decrease produced by KorA on PtrwH) (Supporting Fig. S2). Interestingly, previous work on StbABC showed that this operon balances plasmid partition and conjugation [23]. Results presented here indicate that StbA acts as a common regulator for genes involved in the vegetative and conjugative functions of the plasmid.
Fig. 3. Negative feedbacks and topology of plasmid R388 transcriptional network. 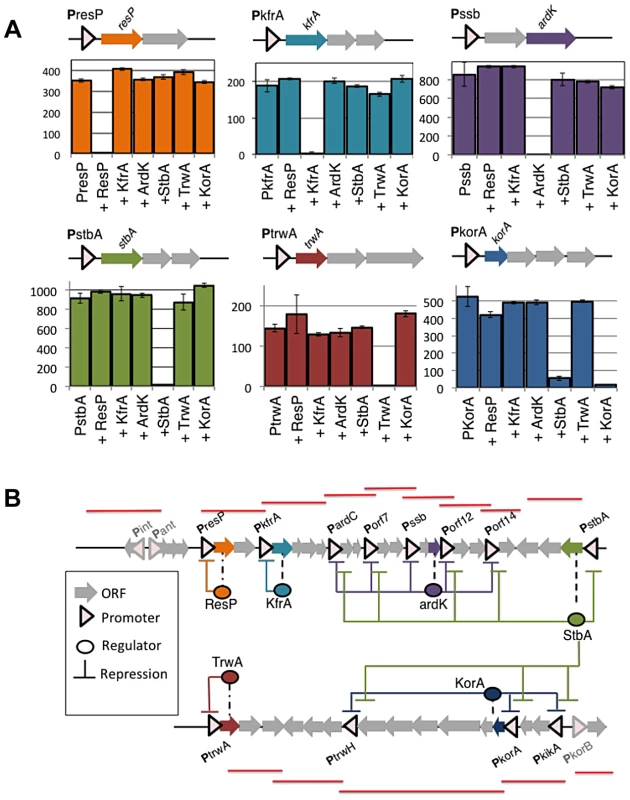
(A). Each panel shows the transcriptional activity (GFP/OD) (×102) of a given promoter, either alone or in the presence of each of the six transcriptional repressors (ResP, KfrA, ArdK, StbA, TrwA and KorA). Repressors were produced from a co-residing expression vector pBAD33, and the negative control indicates the GFP/OD (×102) values obtained in the presence of the empty vector. The upper diagrams show the location of each regulator with respect to its cognate promoter in plasmid R388 (B) A graphical representation of expression profiling data (shown in Supporting figures S3 and S4) unveils the topology of the regulatory circuitry. Coloured arrows indicate the position of transcriptional regulators within plasmid R388 genome (ResP in orange, KfrA in blue, ArdK in purple, StbA in green, TrwA in red and KorA in navy blue). The regulatory links are coloured according to the same code. Red lines shown over the ORF map correspond to the transcriptional units identified in Figure 2. These results allowed us to determine the topology of plasmid R388 transcriptional network, which is depicted in Figure 3B. The network is completely dominated by negative repression, and promoter activation will depend on signals levering the action of plasmid repressors. In order to identify the signals that the network responded to, we challenged the plasmid with a plethora of environmental changes. We modified growth medium (LB, minimal M9), temperature (30, 37 and 42°C) and tested the presence of stressing agents, like sub-inhibitory concentrations of antibiotics and common triggers of the SOS response (Materials and Methods). As judged from fluorescent expression profiling, none of these signals was found to specifically activate any promoter in the network (Supporting figures S3, S4 and S5). The possible effect of Escherichia coli recipient cells was also tested by co-culture in liquid media with plasmid free cells (Supporting figure S6). Since plasmid R388 can only conjugate on solid surfaces [24], these conditions prevented horizontal transfer of the plasmid, while allowing the donors to sense any potential signal from the recipient cells. Again, the regulatory network was unresponsive (Supporting figure S6), indicating that, in the conditions tested, the network did not respond to any diffusible signal from the recipient cells. Altogether these results indicated that plasmid R388 does neither respond to pheromones (unlike many plasmids from Gram + bacteria [15]), nor quorum sensing signals (unlike Ti plasmids from Agrobacterium [16], [17]) nor SOS inducing agents (like many phages and ICEs [25])
The absence of responses against environmental challenges, DNA damage or quorum signals suggested that plasmid regulation is disconnected from the main sensory circuitry of the host cell. However, sensing is not the only function that transcriptional regulation can undertake; generating temporal programs, or guarding the cell homeostasis are also adaptive functions that arise purely from the internal dynamics of regulatory systems. In order to study the internal dynamics of the plasmid network, we used a simple quantitative model. Since all transcriptional regulators in the plasmid were self-repressors (Figure 3), we used a simple ordinary differential equations (ODE) model of a negative feedback loop. Let X denote the mRNA and Y the protein concentrations for a given feedback loop, the system of differential equations that describe the system follows:
This equation is based on the assumption that, in the absence of repressor binding, mRNA is transcribed at rate λ1, and translated at rate λ2. Repressor binding is modelled following simple mass-action kinetics. This binding is characterized by a half maximal binding constant k, which is the ratio between the dissociation and binding constants (k = koff/kon). The model allows cooperative binding, with cooperativity index n (n = 1 for non cooperative binding). Parameters β1 and β2 correspond to the degradation rates of mRNA and the regulator, respectively. This simple ODE model has been extensively used in the literature, and was shown to confer different properties, such as decrease the response time and increase the stability of transcriptional sensory systems[26], [27]. These properties are characteristic of negative feedback loops whose components (mRNAs and proteins) are in steady state. However, apart from these and other steady-state properties, NFLs are known to exhibit transient behaviours while adjusting to the steady-state. In electrical engineering it is well known that NFLs can overshoot before reaching steady-state when they start from initial zero conditions (x = 0 , y = 0 at t = 0). In biological contexts, this property has received little attention, the reason being that daughter cells inherit not only the chromosome but also a proportional part of its regulatory elements. Thus, in the normal life of bacteria, transcriptional NFLs do not usually experience situations with zero concentration of its constituents. However, conjugative plasmids have a specific mechanism of invasion, entering a cell in the form of ssDNA, without accompanying mRNAs or transcriptional regulators. Simulations of Eq 1. mimicking these conditions produced an overshoot, showing that both the mRNA and the protein experienced a transitory burst and then relaxed to their steady state values (Figure 4A). While mathematical analysis indicated that a temporal lag between the mRNA and the protein was enough to produce overshooting (Supporting Text S1), computational analysis indicated that the magnitude of this overshoot is heavily dependent on the parameters of the system. Defining the magnitude of the overshoot as the ratio between the maximal levels reached by X (Xmax) and the value of X at steady state (Xss), simulations showed that increasing the promoter strength (λ) or decreasing K (increasing the strength of the repression, i.e. the affinity of the regulator for its cognate site) increased correspondingly the size of the transcriptional overshoot (Figure 4A). This dependency strongly suggested that there should be a correlation between the overshoot and the relative strength of the repression exerted by the NFL. The relative strength of the feedback can be expressed in terms of feedback gain (G) (Figure 4B). We define G as the ratio between the steady states shown by the open loop (without the repressor) and the closed loop (with the repressor)
Fig. 4. Transcriptional overshooting and its relationship with feedback gain. 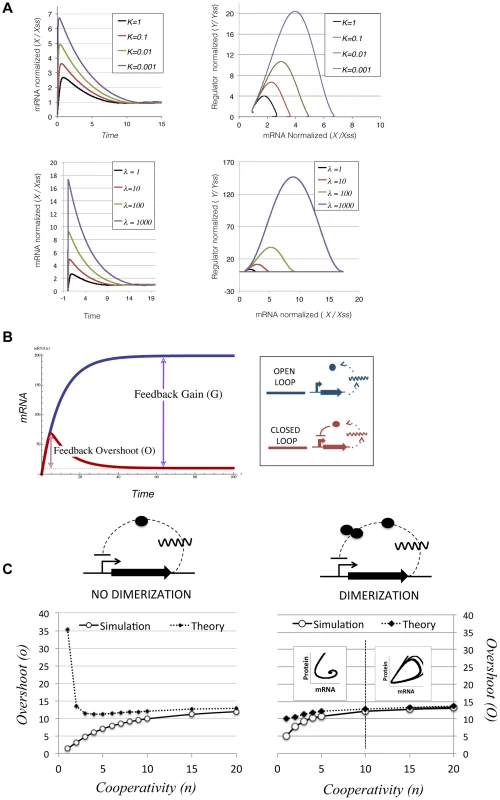
(A) Numerical simulations showing the effect of increasing feedback gain on the magnitude of the transcriptional overshoot. Left panels show the relative abundance of mRNA (X) normalized by its steady-state value (Xss) along time. Right panels show the phase-plane portrait of the system, where the x axis corresponds to the normalized mRNA values (variable X in Ec.1) and the y axis corresponds to the normalized regulator levels (variable Y in Ec.1). Values were normalized by their respective steady-state levels. Upper panels show the effect of increasing the feedback gain by decreasing the feedback constant K. Simulations were performed with λ1 = 10, β2 = 0.2, λ2 = 10, β1 = 1 and n = 1. Lower panels show the effect of increasing the feedback gain by increasing the intrinsic transcription rate λ1. Simulations were performed with λ1 = 0.01, β2 = 0.2, λ2 = 10, β2 = 1 and n = 1. The figure shows that the maximal values of X and Y grow as the feedback gain is increased, either by decreasing K or increasing λ1 (B) Scheme showing the theoretical time evolution of an open loop (blue) and a closed negative feedback loop (red). The feedback gain (G) corresponds to the ratio between the steady states of both systems, being all parameters equal (blue dashed line). The overshoot (O) corresponds to the transient production above the steady-state levels experienced by the closed loop when starting from initial conditions t = 0, x = 0, y = 0 (red dashed line) (C) Performance of the theoretical approximation described in Ec. 4 , compared to numerical simulations. Both panels show results obtained by numerical integration of Ec.1 (white dots) and predicted overshoots obtained from Ec. 4 (black dots). All simulations and calculations were done in a system with parameters k = 0.01, λ1 = 10, β2 = 0.2, λ2 = 10, β1 = 1 and changing the cooperativity of the repression (n, x axis). The left panel corresponds to a system where regulator Y is allowed to repress its own synthesis immediately after translation, while the right panel corresponds to the same system but including the requirement of Y dimerization before binding to DNA. Dimer formation is simulated by a simple ODE with Ka = 0.1 and Kd = 0.01. The inner graphs on the right chart show the phase-portrait of the system, with mRNA on the x axis and regulator concentration on the y axis. As shown in the figure, when the number of binding sites is higher than n = 10 the system becomes cyclostationary, opening the possibility of periodical bursts of transcription. This expression indicates that the feedback gain is directly dependent on the transcriptional/translational strength (λ1 λ2) and inversely correlated to the feedback constant k. Similarly, the overshoot (O) can be expressed as the ratio between the maximum value on X divided by its steady state. Then, by linearizing X before the onset of the repression loop we can approximate O as:
This approximation indicates that the stronger the gain (G) the higher the overshoot will be. This approximation holds for highly non-linear systems, with high values of n (Figure 4C, left panel). However, if we introduce a dimerization step where two monomers of repressor Y need to interact to form an active dimer, the approximation holds for all n (Figure 4C, right panel). The fact that nearly all transcription factors from Prokaryotes act as multimers indicates that this is a conservative assumption [28]. Equation 3 indicates that O is proportional to the gain G, and to the time to reach the maximal value of X (in the limit t = = >∞, e−βt≈0 and O≈G). This means that O increases with higher delays, and the higher the feedback gain, the more prominent the transcriptional overshoot will be. Previous computational analysis of other feedback loops showed similar dependencies between the intensity of the overshoot and the strength of the feedback gain [29]. Therefore, simulations and theory predicted that a network architecture based on strong promoters, tightly repressed in negative feedback loops, would exhibit significant transient overshooting after HGT. For more complex circuits of the plasmid network that are under the control of two transcriptional regulators, transient overshooting is also expected (Supporting figure S7). Due to the OR logic that rules these circuits, the overshooting was dependent on the transcriptional regulator that first achieved its effective values. This, in turn, will depend of its affinity for the target promoter (k) and its own transcriptional/translational strength, as in simple NFLs.
To test whether this transcriptional overshoot could be detected experimentally, we determined mRNA expression levels during conjugative transfer of the plasmid. Conjugative mixes with 1∶1 donor/recipient cell ratio were allowed to mate for 0, 30, 60, 90 and 120 min. Total RNA was extracted from time samples, and expression levels from the main plasmid operons were measured by RT-qPCR. Expression levels were normalized by the results obtained from a constitutive chromosomal gene (dxs). In order to check for possible mRNA increases due to conjugative replication of the plasmid, we measured the relative increase in non-transcribed regions (oriT), and also in promoters that were not negatively regulated (dhfR gene, controlled by Pant). Experimental procedures are detailed in materials and methods. Results, shown in figure 5, indicated that the expression levels of oriT and dhfR showed limited changes, while genes controlled by negative regulation (resP, ardC, ssb, klcB, trwA and trwF) increased their relative abundance immediately after conjugation. Experimental results showed that those genes that showed the highest induction (trwF, ardC, ssb and klcB) corresponded to promoters with the higher gains (PtrwH, PardC, Pssb and Porf12). On the other hand, those promoters with lower gains (PtrwA and PresP) also yielded lower overshoots (trwA, repA in fig. 5), as predicted by theory. Since conjugation is inherently asynchronous (newly formed transconjugants become donors and infect new receptors), our population measurements resolved poorly the actual kinetics of the overshoot. Also, the kinetics of the overshoot for individual NFLs will depend critically on the mRNA half-life (Eq.3), which is also likely to be variable from gene to gene. As a consequence, the decrease in the overshoot is only observable in some of the genes tested (ardC, ssb,trwH trwA). However, steady-state measurements (equivalent to time 0 in figure 5) indicated that all promoters would eventually return to basal levels. For the klcB gene, controlled by Porf12 promoter, which yielded no observable overshoot, it is not possible to state at this point whether the overshoot was obscured by population effects, or the parameters of this promoter did not yield any significant overshoot.
Fig. 5. Promoter induction after horizontal transfer of the plasmid. 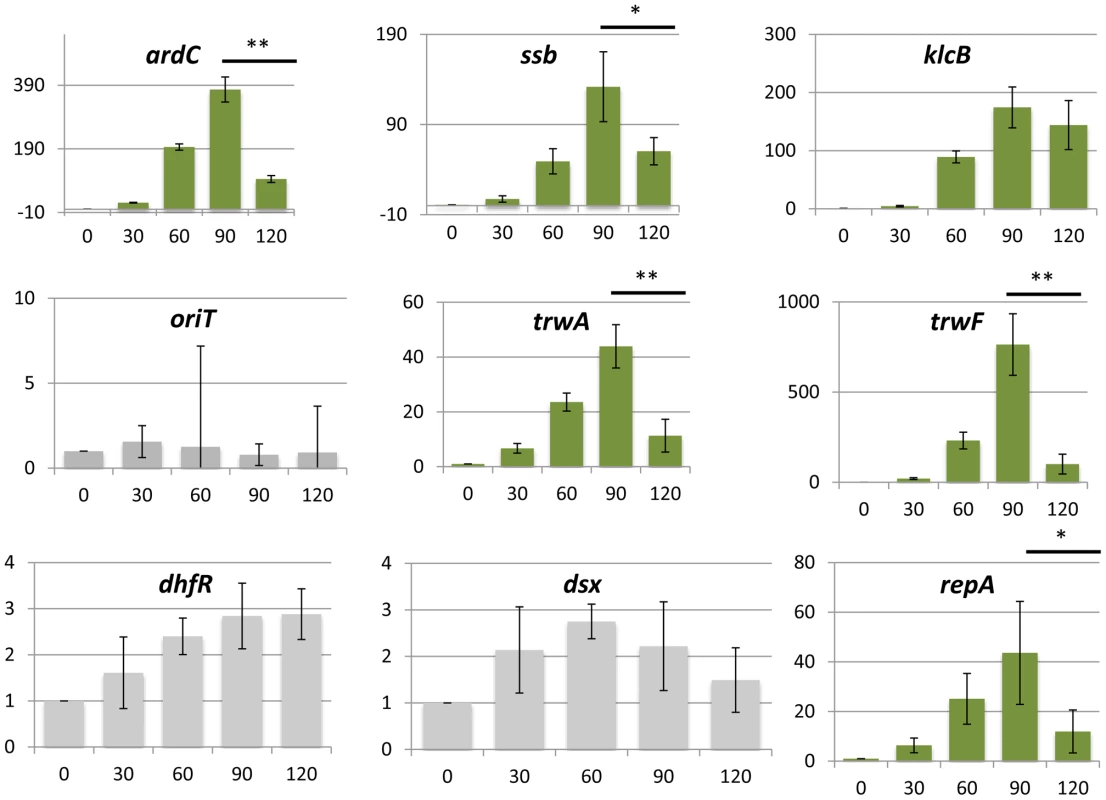
RT-qPCR was used to measure mRNA levels. Bars indicate the relative ratio of mRNA at each time point compared to the values obtained in the absence of conjugation (time 0). Asterisks indicate the statistical significance of the differences observed * = p<0.1, ** = p<0.05 Experimental procedures and calculations are detailed in Materials and Methods and expanded results are shown in Supporting Figure S4. Measurements represent the average of three independent mRNA extractions. This transient induction could have phenotypic effects on the host cell. Plasmids impose a burden on the host, meaning that, in the absence of positive selection for plasmid-encoded traits like antibiotic resistances, plasmids must survive as parasitic entities [30], [31], [32]. It is conceivable that a transient increase in plasmid gene expression will translate into a higher burden to the host cell. To test whether any effect on host fitness could be observed, we measured the growth rates of donor, recipient and transconjugant cells, immediately after conjugation. We used two spontaneous Rifr and Nxr mutants of E.coli strain Bw27783, which showed no observable differences in growth rate (figure 6A). Cells from both strains that had carried the plasmid for at least 10 generations exhibited a 17% increase in the generation time when compared to plasmid free cells (Figure 6A). This indicated that the plasmid exerted a measurable burden on the host Plasmid conjugation assays were performed on LB agar surfaces in a 1∶1 donor/recipient ratio, and cells were allowed to mate for 30 min. Conjugation was stopped by resuspending cells from the solid surface, cells were diluted to OD600≈0.01 in fresh LB, placed in agitation at 37 C and allowed to grow for 5 h (Figure 6B). Growth rates were measured by plating on selective antibiotics (materials and methods). Plasmid R388 does not conjugate in liquid media, thus any variation in the proportion of donors, recipients and transconjugants must be due to relative differences in growth rates. Results, shown in figure 6C, indicated that transconjugant cells suffered a remarkable decrease in growth rate immediately after conjugation, showing a first generation time of about 2.5× times that of donor cells. However, after this long first generation, transconjugant cells recovered, achieving the same number of divisions as donor cells for the total duration of the experiment (7 generations). Similar results were obtained when donor and recipient strains were reversed (Supporting Figure S8). The observed growth deficit in the transconjugants could be a by-product of the conjugation mechanism, which requires the piercing of the recipient cell by the transfer apparatus. To test whether this was the case, we carried out a similar experiment with a mobilizable plasmid. In this case, a small cloning vector carrying just the origin of transfer (oriT) of plasmid R388 was mobilized into recipient cells by means of an oriT− mutant of plasmid R388. Under these conditions, plasmid R388 does not move itself, but is still able to produce a conjugative pilus and thus mobilize the small vector into the recipient cells. Results show that vector mobilization did not produce a significant decrease in the growth rate of transconjugant cells (Supporting Figure S8). This indicated that the transitory deficit in growth rate was not due to cell injuries produced by the mechanism of conjugation, but was a consequence of the entry of the conjugative plasmid inside the recipient cell.
Fig. 6. Transconjugants experience a growth deficit immediately after conjugation. 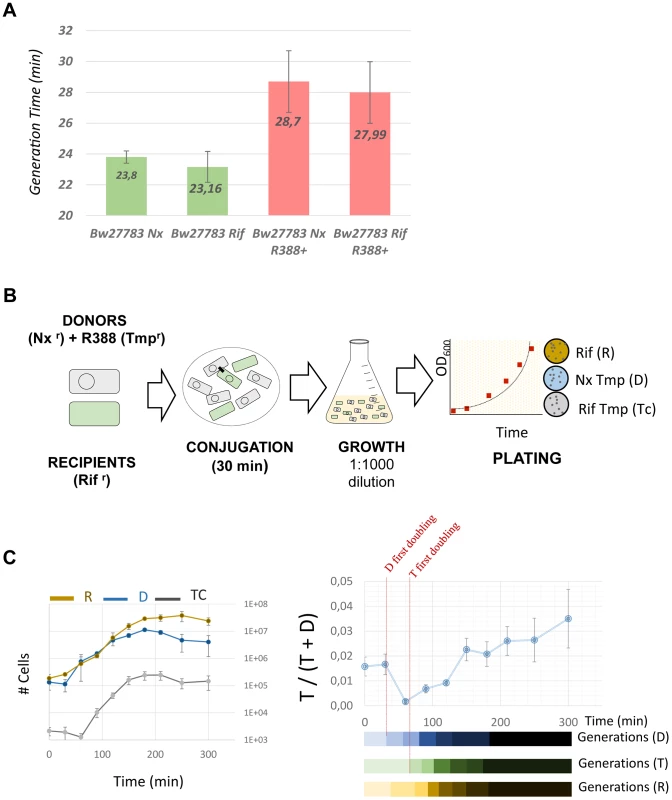
(A) Generation times (in minutes) of E.coli Bw27783 with or without plasmid R388. Results represent the average and standard deviation of 12 experiments. (B)Scheme showing the experimental design to test the effect of plasmid conjugation in early transconjugants. Donor and recipient cells were grown in LB broth in the presence of selective antibiotics and mixed in 1∶1 conjugations on LB-Agar. Conjugation was allowed to take place for 30 minutes and cells were resuspended in fresh LB. Plate counting was used to determine de number of donors (D) recipients (R) and transconjugants (Tc). (C) Results of the competition experiments between D, R and Tc cells. (Left panel) Absolute numbers (cells/ml) of each species along the time course of the experiment. Each data point was measured by triplicate. (Right panel) Proportion of plasmid containing cells that are transconjugants along the time course of the experiment. Since plasmid R388 does not conjugate in liquid media, all variations in the relative proportions of Tc cells to D and R cells must be due to differences in growth. Results show a decrease in the relative abundance of Tc cells compared to D cells, that recovers after t = 90 minutes. The lower bars indicate the apparent generation times for each cell type calculated from data shown on the left panel. Discussion
The intensity of HGT in the microbial world, and the prevalence of plasmids in nature indicate that plasmids are successful in colonizing microbial populations. Yet multilevel selection imposes opposing demands on plasmid physiology that require a delicate equilibrium between the expression of plasmid functions and the burden imposed on the host cell [9]. Understanding the regulatory mechanisms of plasmid transcriptional control might shed light on the way plasmids conciliate these requirements.
In this work we describe the topology and dynamics of the transcriptional network of plasmid R388, the smallest BHR plasmid from Proteobacteria. The network consisted exclusively of transcriptional repressors. This preference for transcriptional repression is in contrast with the situation described for the regulatory networks of bacterial chromosomes. For example, in E.coli the number of transcriptional activators roughly equals the number of repressors [33]. However, other transcriptional networks from BHR plasmids, like plasmid RP4, were also found to depend solely on transcriptional repressors [11]. In plasmid R388, transcriptional repression was exerted mainly in the form of negative feedback loops. These feedback loops showed high gains (defined as the ratio between the expression levels of the open and the closed feedback loops). Although we are not aware of any systematic, quantitative study of a plasmid regulatory network, several independent studies have reported that the regulatory network of plasmid RP4 contains strong promoters that are kept tightly repressed by the plasmid regulators [14], [34], [35],[36],[37],[38]. Remarkably, plasmids R388 and RP4 show similar broad host ranges, but they are not phylogenetically related [3], [4], [39]. This indicates that both plasmids, which presumably suffer from analogous selective constrains, have independently evolved transcriptional networks with analogous topologies.
Simulations and theory indicate that whenever a negative feedback loop has a gain higher than 1 and a certain time delay between the mRNA and the regulatory protein, the system would show transient overshooting (Eq 3 and figure 4A). The actual production of the overshoot requires the system to begin with zero initial concentration of transcriptional repressors (t = 0, x = 0, y = 0, in Eq 1), allowing the separation of timescales to produce a period of repressor-free transcription. For conjugative plasmids, this situation is met every time the plasmid enters into a new cell by conjugation. In fact, any negative feedback loop that undergoes conjugation is likely to experience transient overshooting. It has been known for a long time that a lysogenic phage transferred by Hfr conjugation (an artificial system that allows the horizontal transfer of the entire chromosome), can become lytic when entering into a new host [40]. A similar behavior was also observed when an RFP-TetR autogenously regulated cassette was inserted in the E.coli chromosome and transferred by Hfr conjugation into a new cell [41]. Transient overshooting is therefore an epiphenomenon associated to negative feedback loops that experience some sort of “genome rebooting”, a condition where the transcriptional/translational machinery is present, but the regulatory network is transitory absent.
Simulations and theory also indicated that the overshoot is expected to be higher whenever the feedback loop has a high gain. Plasmid promoters were shown to contain feedback loops with characteristic high gains. RT-qPCR analysis showed a transcriptional burst in 5 out of 6 plasmid promoters subjected to NFLs, when the plasmid transferred horizontally into a new population (Figure 5). Untranscribed regions (oriT), or plasmid genes that were not under the control of a negative regulator (dhfR), did not show similar increases (Figure 5). This indicates that the observed effect is not due to conjugation increasing the abundance of plasmid molecules within the population. Moreover, given that the conjugative mix contained a 50% ratio of donor/recipient cells, the maximal increase that conjugation could cause is 2-fold. The increase of mRNA abundance was not due to cell growth either, since results were normalized by the increase experienced by a constitutively expressed chromosomal gene (dxs). Gene dxs showed a maximal increase of 2-fold, indicating that cell growth is a minor contributor to the observed bursts in mRNA levels. These results cannot be considered absolute quantifications of the transcriptional overshooting, because our measurements involved entire populations (which contained donor and recipient cells), and bacterial conjugation is an asynchronous process. However, although our quantitative results might be blurred by population effects, the general trend predicted by theory and simulations was sound: those promoted that showed higher gains also showed the higher overshoots.
Plasmids are known to produce fitness deficits on their hosts. This effect has been usually ascribed to the metabolic burden imposed by expression of plasmid genes. Therefore, any increase in expression levels caused by transient overshooting might have its counterpart in the growth rate of the host cell. We measured the growth rates of newly formed transconjugants and found that the plasmid induced a deficit that was transitorily high (250% increase in generation time), relaxing later to a 17% increase compared to plasmid free cells. This was not caused by any physical damage produced by the mechanism of conjugation, and correlates in time with the induction of plasmid genes after transfer. Altogether, these results strongly suggest that overshooting after HGT has a measurable impact on the host growth rate. Although this kind of effect has been traditionally ascribed to metabolic burden, it is also possible that the toxic effects of specific plasmid proteins could contribute. Since the growth deficit roughly corresponds to the time of overshoot decay (figure 5 and figure 6C) the most plausible explanation is that growth deficit be caused by the transcription/translation of the plasmid genes. This would also explain why, when the recipient cells recover, they grow as fast as recipient cells for a few generations.
One intriguing question then is why has the plasmid evolved a network based exclusively on NFLs, when this motif is likely to overshoot after conjugative transfer, temporarily hampering the host growth rate? Other broad host range plasmids show convergent architectures, suggesting that despite this temporary fitness deficit, negative feedback might have some adaptive property for the plasmid lifestyle. Indeed, negative feedback has been shown to exhibit a number of adaptive properties, speeding up the response time of sensory regulatory networks [27], reducing transcriptional noise [42], [43], driving noise to higher frequencies and allowing easier filtering [44]. Speeding up the response is a property associated to sensory systems, and so far the plasmid network has not shown responses to any specific signals. Noise control might be more interesting for plasmids, given that plasmid replication is extremely sensitive to fluctuations [45], [46]. However this problem is restricted mainly to replication, and does not explain why the same regulatory strategy is widespread in the entire plasmid backbone.
It is also possible that transient overshooting provides an adaptive benefit for the particular lifestyle of conjugative plasmids. Plasmids spread horizontally, by invading new cells, and vertically, as the host cell reproduces. Like many other parasites that share this double reproductive strategy, plasmids suffer from opposing selective forces, summarized in the observation that increased infectivity usually results in increased virulence. This inverse relationship is well known in plasmids and phages [30], [31], [32], and if a given plasmid increases the expression levels of its own plasmid products (especially those that are cis-acting), it would also increase its intracellular fitness, at the cost of penalizing the host [9]. Penalizing the host, in turn, decreases the ability of the host cell to compete with its neighbours [9], and thus the plasmid experiences lower vertical transmission rates. Although both selection processes are intrinsically in conflict, the timescales involved in each of them are different. The decrease on host fitness imposed by the plasmid metabolic burden is usually low (% in the case of plasmid R388), meaning that intercellular selection acts by the accumulation of small fitness deficits over long periods of time [5], [6], [8]. On the other hand, intracellular selection is more pronounced in the initial stages of infection, since a cell that has received the plasmid is still susceptible to superinfection until the surface exclusion systems have been deployed [9] [47]. Therefore, it is in the interest of the first plasmid that enters into a cell to block the entrance of other plasmid copies, and to reach the steady-state copy number as soon as possible. Transcriptional overshooting after HGT would allow the plasmid to produce a vigorous transcriptional response when intracellular selection is more acute. The transient nature of this response would guarantee that the long-term effects on intercellular selection are minimized. Indeed competition experiments showed that, despite the severe initial effect on the host growth rate, transconjugants recovered quickly and were able to achieve the same number of cell divisions as the original donors. Note also that since transconjugants are able to act as donors, conjugation results in an infectious process that proceeds geometrically in the population. If overexpression of conjugative functions results in increased transfer efficiency, a transient overshoot would provide the invading plasmids with higher infectivity. This property will be maintained as long as new cells are infected. If the availability of possible receptors decreases, the overshoot transient nature guarantees that the plasmid population relaxes to a “silent” state, minimizing the burden on the host and improving vertical transmission. Such a mechanism would provide the plasmid population with a mechanism to switch from horizontal to vertical reproduction modes depending on the availability of susceptible receptors. Other lines of evidence also point to this possibility. The stbABC operon of plasmid R388 has been shown to balance the requirements for vegetative stability and conjugative transfer [23]
The fact that transient overshooting is linked to genome rebooting is also interesting from a synthetic biology perspective. Plasmids are nature counterparts of genomic transplantations. In fact, they can be considered as genetic devices for the unidirectional injection of genomes into suitable recipient cells. So far, efforts to transplant whole chromosomes have been restricted to species that share a high degree of genomic identity [48]. A close phylogenetic relationship implies that the regulatory networks of both species might show some cross-reactivity, which could be necessary to control the transplanted chromosome until it has built up its own regulatory system. Distantly related species, however, might show no cross-reactivity between their regulatory networks. Broad host conjugative plasmids are able to invade a wide variety of distantly related species. If we want to expand the range of possible transplants, we need to deal with problems identical to those faced by conjugative plasmids. In particular, how can a genome start up from just DNA and the transcriptional/translational machinery? Negative regulation, with high feedback gains and transient overshooting might be the solution evolved by natural plasmids.
Materials and Methods
Promoter library construction
Strains used were Escherichia coli C41 (ompT hsdSB (rB− mB−) gal dcm (DE3)), E. coli Bw27783 (lacIqrrnB3 ΔlacZ4787 hsdR514 Δ(araBAD)567 Δ(rhaBAD)568 Δ(araFGH) Φ(ΔaraEp PCP8-araE)) [49] and E. coli JM109 (recA1, endA1, gyrA96, thi, hsdR17, supE44, relA1, Δ(lac-proAB)/F′ [traD36, proAB+, lacIq, lacZΔM15]) Primer oligonucleotides (Supporting table S2) were designed to flank each R388 intergenic region longer than 30 bp, according to R388 genomic sequence (Genbank accession number BR000038) and purchased from Sigma. R388 plasmid DNA was extracted using Sigma GenElute Miniprep kit and used as template for PCR amplification. PCR amplification was carried out with Vent DNA polymerase (Biolabs) and consisted of 95°C for 10 min, then 28 cycles of 95°C for 30 s, 55°C for 30 s, 72°C for 30 s and a final step of 72°C for 5 min. PCR products were digested with XhoI and BamHI at 37°C for 2 h and the products purified using QIAquick Gel Extraction Kit (Qiagen). Digested and purified fragments were ligated into pUA66 plasmid DNA using T4 ligase (Roche) with overnight incubation at 16°C. Transformation was accomplished by electroporation into Bw27783 strain. Transformants were selected in LB-agar plates containing 25 µg/ml kanamycin. Positive colonies were detected by PCR using pZE0.5 and pZE0.6 primers. DNA from positive colonies was extracted and insertions sequenced using the same primers as above. The set of reporter plasmids obtained is indicated in Supporting table S2.
Plasmid R388 was transferred to the reporter strains by conjugation. Donor bacteria were E. coli JM109 containing plasmid R388 and recipient bacteria were E. coli BW27783 containing the corresponding reporter plasmid. Conjugations were carried out as previously described [50].
Fluorescent expression profiling
Transcriptional activity was determined by GFP expression profiling as described in [51]. Reporter strains were inoculated into enriched M9 Medium (M9 + casaminoacids 0.2%+ glycerol 0.5%) to which kanamycin (25 µg/ml) was added. To test the effect of subinhibitory concentrations of antibiotics, we used rifampicin and chloramphenicol following the protocol described in [52]. Results represent the average of at least 4 independent measurements. The S.O.S. response was induced exposing the cells to 5 or 10 seconds of UV light (254 nm, 15W). Mitomycin C was used at a final concentration of 5 µg/ml.
Effects of regulatory proteins
Selected R388 ORFs containing potential transcriptional regulators were PCR amplified with primers indicated in table S1. The resulting DNA segments were cloned in plasmid pET3a (Addgene). The genetic manipulation techniques were the same as those described above, except that NdeI and BamHI restriction endonucleases were used for cloning PCR products in pET3a expression vector. After transforming to Escherichia coli C41 strain, protein expression was induced by adding 0.1 mM IPTG to exponentially growing cultures and visualized by denaturing polyacrylamide gel electrophoresis (data not shown). Then each gene was subcloned in plasmid pBAD33 using XbaI-Hind III endonucleases. Plasmids obtained (table S2) were transformed to E. coli Bw27783 containing the corresponding reporter plasmids for further analysis. To determine the effect of potential regulatory proteins, pAR expression plasmids (Supporting table S2) were transformed into E. coli Bw27783 containing the corresponding reporter plasmid. Protein expression was induced by adding appropriate concentrations of arabinose [51] to M9-broth and fluorescence per OD unit (GFP/OD) was determined and compared to that produced by the same reporter strain when containing the empty expression vector pBAD33.
Quantification of mRNA levels
Total RNA was extracted from E.coli Bw27783 containing plasmid R388 and grown in LB media at 37C. Cells were harvested at OD600 = 0.5 and RNA was extracted using RNAEasy kit (Quiagen). Total RNA concentration was quantified using Experion RNA StdSens Analysis kit (Biorad). cDNA was obtained by reverse transcriptase (Omniscript, Qiagen) and the relative concentration of the target genes was determined by qPCR (ICycler, Biorad) using the IQ SYBR Green Supermix kit (Biorad). To determine the cDNA abundance, the threshold cycle (Ct) was determined using the ICycler software. A total of 66 primer pairs were manually designed to cover the entire genome of the plasmid, and the efficiency of each primer pair was determined measuring the Ct obtained from 3 different DNA concentrations (2.5, 5 and 10 ng). The sequence and efficiencies of each primer is shown in Supporting table S2. cDNA reactions were performed from 300 ng total RNA concentration and results were normalized by the Ct obtained from 5 ng of plasmid DNA purified by alkaline lysis.
RT-qPCR measurements of gene expression during conjugation
To determine the relative expression of plasmid genes during conjugation, 1 ml samples of donor (E.coli Bw27783 +R388 plasmid) and recipient (E.coli Bw27783) cultures were mixed in a 1∶1 ratio, pelleted and resuspended in 100 l of fresh LB. Cells were then spread on LB-Agar and incubated at 37C for 30, 60 or 90 min. After each conjugation period, cells were resuspended in 2 ml of fresh LB and total RNA was extracted as described in the previous paragraph. Primer pairs used are shown in supporting table. S2 For each independent experiment measurements were performed in duplicate, and a total of 4 independent experiments were performed for each time point. In order to avoid artefacts introduced by cell manipulation, the RNA concentration at time 0 was determined following the same manipulation procedure, but cells were immediately resuspended after being plated in LB-Agar. The relative concentration of target RNAs (r) was determined by r = E(ΔCt) where E is the efficiency of the primer pair, calculated as in [21], and ΔCt = CtT = t−CtT = 0. Results were normalized to the increase experienced by a chromosomal gene (dxs) using the ΔCt method, where ΔCt = (CtT = t−CtT = 0)probe [21]. Relative error was propagated using the standard propagated error formula. For the relative amount of a test mRNA (Ct) with respect to a given standard (Ctdxs) the aforementioned formula yields σx/<x> = ln(2) (var(Ct)+var(Ctdxs)−2cov(Ct,Ctdxs))−2 , where var stands for the variance and cov for the covariance. The statistical significance was ascertained using a one handed t test.
Competition after conjugation experiments
Two spontaneous mutants resistant to rifampicin and nalidixic acid from E.coli Bw27783 were obtained by plating in selective antibiotics. The stability of the mutation was tested and the strains were used as donor/recipients in conjugation experiments. Growth rates were determined from cells growing in LB broth at 37 C with agitation, and results showed that both strains had indistinguishable division times in such conditions (n = 12). In order to measure the growth rate of donor, recipient transconjugant cells, we performed conjugations for t = 30 minutes. Saturated cultures, grown overnight in LB at 37C, were and diluted 1/1000 in fresh LB until cells reached an OD600 of 0.1. Donor and recipient cells were mixed in a 1∶1 ratio and concentrated 1000 times. A total of 15 microliters were deposited onto a LB agar plate and let at 37C for 30 minutes to allow plasmid transfer. Cells were then resuspended in 3 ml of LB broth and allowed to grow at 37C with agitation. Time samples were obtained every 30 min, and cells were diluted in 1×PBS to count the number of donor, recipients and transconjugants by plating in selective antibiotics. Plating of early time points was performed 30 minutes after PBS resuspension, to allow the antibiotic markers to express to adequate levels. We checked that this treatment did not artificially increased the number of cells due to growth in the PBS dilution. We plated dilutions from 10−1 to 10−6. The error introduced by the dilution was measured obtaining values typically around cv = 0.1–0.2. This error was propagated to the actual number of cells and accounts for most of the variability observed in the results.
Computational analysis
Numerical integration of the ODE system was performed in Matlab (Mathworks) using the ODE23 algorithm. ODE23 is a Runge-Kutta algorithm with automatic step size. The absolute and relative tolerances were set at 10−10 , tspan = 1000.
Supporting Information
Zdroje
1. FrostLS, LeplaeR, SummersAO, ToussaintA (2005) Mobile genetic elements: the agents of open source evolution. Nat Rev Microbiol 3 : 722–732.
2. de la CruzF, DaviesJ (2000) Horizontal gene transfer and the origin of species: lessons from bacteria. Trends Microbiol 8 : 128–133.
3. Fernandez-LopezR, Garcillan-BarciaMP, RevillaC, LazaroM, VielvaL, et al. (2006) Dynamics of the IncW genetic backbone imply general trends in conjugative plasmid evolution. FEMS Microbiol Rev 30 : 942–966.
4. SenD, BrownCJ, TopEM, SullivanJ (2013) Inferring the Evolutionary History of IncP-1 Plasmids Despite Incongruence among Backbone Gene Trees. Molecular biology and evolution 30 : 154–166.
5. BoumaJE, LenskiRE (1988) Evolution of a bacteria/plasmid association. Nature 335 : 351–352.
6. DionisioF, ConceicaoIC, MarquesAC, FernandesL, GordoI (2005) The evolution of a conjugative plasmid and its ability to increase bacterial fitness. Biol Lett 1 : 250–252.
7. De GelderL, PoncianoJM, JoyceP, TopEM (2007) Stability of a promiscuous plasmid in different hosts: no guarantee for a long-term relationship. Microbiology 153 : 452–463.
8. HaftRJ, MittlerJE, TraxlerB (2009) Competition favours reduced cost of plasmids to host bacteria. ISME J 3(7): 761–9.
9. PaulssonJ (2002) Multileveled selection on plasmid replication. Genetics 161 : 1373–1384.
10. ThomasCM, NielsenKM (2005) Mechanisms of, and barriers to, horizontal gene transfer between bacteria. Nat Rev Microbiol 3 : 711–721.
11. BingleLE, ThomasCM (2001) Regulatory circuits for plasmid survival. Curr Opin Microbiol 4 : 194–200.
12. PolzleitnerE, ZechnerEL, RennerW, FratteR, JaukB, et al. (1997) TraM of plasmid R1 controls transfer gene expression as an integrated control element in a complex regulatory network. Mol Microbiol 25 : 495–507.
13. KoraimannG, TeferleK, MarkolinG, WogerW, HogenauerG (1996) The FinOP repressor system of plasmid R1: analysis of the antisense RNA control of traJ expression and conjugative DNA transfer. Mol Microbiol 21 : 811–821.
14. ThomasCM (2006) Transcription regulatory circuits in bacterial plasmids. Biochem Soc Trans 34 : 1072–1074.
15. DunnyGM, JohnsonCM Regulatory circuits controlling enterococcal conjugation: lessons for functional genomics. Curr Opin Microbiol 14 : 174–180.
16. OgerP, KimKS, SackettRL, PiperKR, FarrandSK (1998) Octopine-type Ti plasmids code for a mannopine-inducible dominant-negative allele of traR, the quorum-sensing activator that regulates Ti plasmid conjugal transfer. Mol Microbiol 27 : 277–288.
17. McAnullaC, EdwardsA, Sanchez-ContrerasM, SawersRG, DownieJA (2007) Quorum-sensing-regulated transcriptional initiation of plasmid transfer and replication genes in Rhizobium leguminosarum biovar viciae. Microbiology 153 : 2074–2082.
18. SuzukiH, YanoH, BrownCJ, TopEM (2010) Predicting plasmid promiscuity based on genomic signature. J Bacteriol 192 : 6045–6055.
19. ZaslaverA, BrenA, RonenM, ItzkovitzS, KikoinI, et al. (2006) A comprehensive library of fluorescent transcriptional reporters for Escherichia coli. Nat Methods 3 : 623–628.
20. RevillaC, Garcillan-BarciaMP, Fernandez-LopezR, ThomsonNR, SandersM, et al. (2008) Different pathways to acquiring resistance genes illustrated by the recent evolution of IncW plasmids. Antimicrob Agents Chemother 52 : 1472–1480.
21. PfafflMW (2001) A new mathematical model for relative quantification in real-time RT-PCR. Nucleic Acids Res 29: e45.
22. GuynetC, de la CruzF (2011) Plasmid segregation without partition. Mobile genetic elements 1 : 236–241.
23. GuynetC, CuevasA, MoncalianG, de la CruzF (2011) The stb operon balances the requirements for vegetative stability and conjugative transfer of plasmid R388. PLoS genetics 7: e1002073.
24. del CampoI, RuizR, CuevasA, RevillaC, VielvaL, et al. (2012) Determination of conjugation rates on solid surfaces. Plasmid 67 : 174–182.
25. WaldorMK, FriedmanDI (2005) Phage regulatory circuits and virulence gene expression. Current opinion in microbiology 8 : 459–465.
26. CamasFM, BlazquezJ, PoyatosJF (2006) Autogenous and nonautogenous control of response in a genetic network. Proc Natl Acad Sci U S A 103 : 12718–12723.
27. RosenfeldN, ElowitzMB, AlonU (2002) Negative autoregulation speeds the response times of transcription networks. J Mol Biol 323 : 785–793.
28. SchleifR (1988) DNA binding by proteins. Science 241 : 1182–1187.
29. SarkarRR, MaithreyeR, SinhaS (2011) Design of regulation and dynamics in simple biochemical pathways. Journal of mathematical biology 63 : 283–307.
30. LevinBR, StewartFM (1980) The population biology of bacterial plasmids: a priori conditions for the existence of mobilizable nonconjugative factors. Genetics 94 : 425–443.
31. LundquistPD, LevinBR (1986) Transitory derepression and the maintenance of conjugative plasmids. Genetics 113 : 483–497.
32. StewartFM, LevinBR (1977) The Population Biology of Bacterial Plasmids: A PRIORI Conditions for the Existence of Conjugationally Transmitted Factors. Genetics 87 : 209–228.
33. Shen-OrrSS, MiloR, ManganS, AlonU (2002) Network motifs in the transcriptional regulation network of Escherichia coli. Nat Genet 31 : 64–68.
34. Jagura-BurdzyG, ThomasCM (1992) kfrA gene of broad host range plasmid RK2 encodes a novel DNA-binding protein. J Mol Biol 225 : 651–660.
35. Jagura-BurdzyG, ThomasCM (1995) Purification of KorA protein from broad host range plasmid RK2: definition of a hierarchy of KorA operators. J Mol Biol 253 : 39–50.
36. KostelidouK, JonesAC, ThomasCM (1999) Conserved C-terminal region of global repressor KorA of broad-host-range plasmid RK2 is required for co-operativity between KorA and a second RK2 global regulator, KorB. J Mol Biol 289 : 211–221.
37. AdamczykM, DolowyP, JonczykM, ThomasCM, Jagura-BurdzyG (2006) The kfrA gene is the first in a tricistronic operon required for survival of IncP-1 plasmid R751. Microbiology 152 : 1621–1637.
38. BingleLE, RajasekarKV, MuntahaS, NadellaV, HydeEI, et al. (2008) A single aromatic residue in transcriptional repressor protein KorA is critical for cooperativity with its co-regulator KorB. Mol Microbiol 70 : 1502–1514.
39. PansegrauW, LankaE, BarthPT, FigurskiDH, GuineyDG, et al. (1994) Complete nucleotide sequence of Birmingham IncP alpha plasmids. Compilation and comparative analysis. J Mol Biol 239 : 623–663.
40. JacobF, WollmanEL (1956) [Processes of conjugation and recombination in Escherichia coli. I. Induction by conjugation or zygotic induction]. Annales de l'Institut Pasteur 91 : 486–510.
41. BabicA, LindnerAB, VulicM, StewartEJ, RadmanM (2008) Direct visualization of horizontal gene transfer. Science 319 : 1533–1536.
42. BecskeiA, SerranoL (2000) Engineering stability in gene networks by autoregulation. Nature 405 : 590–593.
43. SavageauMA (1974) Comparison of classical and autogenous systems of regulation in inducible operons. Nature 252 : 546–549.
44. AustinDW, AllenMS, McCollumJM, DarRD, WilgusJR, et al. (2006) Gene network shaping of inherent noise spectra. Nature 439 : 608–611.
45. DasN, Valjavec-GratianM, BasurayAN, FeketeRA, PappPP, et al. (2005) Multiple homeostatic mechanisms in the control of P1 plasmid replication. Proc Natl Acad Sci U S A 102 : 2856–2861.
46. ParkK, HanE, PaulssonJ, ChattorajDK (2001) Origin pairing (‘handcuffing’) as a mode of negative control of P1 plasmid copy number. EMBO J 20 : 7323–7332.
47. Garcillan-BarciaMP, de la CruzF (2008) Why is entry exclusion an essential feature of conjugative plasmids? Plasmid 60 : 1–18.
48. LartigueC, GlassJI, AlperovichN, PieperR, ParmarPP, et al. (2007) Genome transplantation in bacteria: changing one species to another. Science 317 : 632–638.
49. KhlebnikovA, DatsenkoKA, SkaugT, WannerBL, KeaslingJD (2001) Homogeneous expression of the P(BAD) promoter in Escherichia coli by constitutive expression of the low-affinity high-capacity AraE transporter. Microbiology 147 : 3241–3247.
50. BollandS, LlosaM, AvilaP, de la CruzF (1990) General organization of the conjugal transfer genes of the IncW plasmid R388 and interactions between R388 and IncN and IncP plasmids. J Bacteriol 172 : 5795–5802.
51. Fernandez-LopezR, Del CampoI, RuizR, LanzaV, VielvaL, et al. Numbers on the edges: a simplified and scalable method for quantifying the gene regulation function. Bioessays 32 : 346–355.
52. GohEB, YimG, TsuiW, McClureJ, SuretteMG, et al. (2002) Transcriptional modulation of bacterial gene expression by subinhibitory concentrations of antibiotics. Proceedings of the National Academy of Sciences of the United States of America 99 : 17025–17030.
Štítky
Genetika Reprodukční medicína
Článek Natural Polymorphisms in Influence Negative Selection and CD4∶CD8 Lineage Commitment in the RatČlánek MicroRNAs Located in the Hox Gene Clusters Are Implicated in Huntington's Disease PathogenesisČlánek Comparative RNAi Screens in and Reveal the Impact of Developmental System Drift on Gene FunctionČlánek Mutation of SLC35D3 Causes Metabolic Syndrome by Impairing Dopamine Signaling in Striatal D1 Neurons
Článek vyšel v časopisePLOS Genetics
Nejčtenější tento týden
2014 Číslo 2- IVF a rakovina prsu – zvyšují hormony riziko vzniku rakoviny?
- Akutní intermitentní porfyrie
- Souvislost haplotypu M2 genu pro annexin A5 s opakovanými reprodukčními ztrátami
- Transthyretinová amyloidóza z pohledu neurologa a kardiologa aneb jak se vyhnout „misdiagnostice“?
- Hypogonadotropní hypogonadismus u žen a vliv na výsledky reprodukce po IVF
-
Všechny články tohoto čísla
- Fifteen Years Later: Hard and Soft Selection Sweeps Confirm a Large Population Number for HIV In Vivo
- The Same but Different: Worms Reveal the Pervasiveness of Developmental System Drift
- Serine Carboxypeptidase SCPEP1 and Cathepsin A Play Complementary Roles in Regulation of Vasoconstriction via Inactivation of Endothelin-1
- Coherent Functional Modules Improve Transcription Factor Target Identification, Cooperativity Prediction, and Disease Association
- A Long-Chain Flavodoxin Protects from Oxidative Stress and Host Bacterial Clearance
- Mammalian E-type Cyclins Control Chromosome Pairing, Telomere Stability and CDK2 Localization in Male Meiosis
- Influenza Virus Drug Resistance: A Time-Sampled Population Genetics Perspective
- Transcriptome-Wide Analyses of 5′-Ends in RNase J Mutants of a Gram-Positive Pathogen Reveal a Role in RNA Maturation, Regulation and Degradation
- Selective Disruption of Aurora C Kinase Reveals Distinct Functions from Aurora B Kinase during Meiosis in Mouse Oocytes
- X Chromosome Control of Meiotic Chromosome Synapsis in Mouse Inter-Subspecific Hybrids
- A Cohesin-Independent Role for NIPBL at Promoters Provides Insights in CdLS
- Extreme Population Differences in the Human Zinc Transporter ZIP4 (SLC39A4) Are Explained by Positive Selection in Sub-Saharan Africa
- Classic Selective Sweeps Revealed by Massive Sequencing in Cattle
- Genomic Networks of Hybrid Sterility
- Natural Polymorphisms in Influence Negative Selection and CD4∶CD8 Lineage Commitment in the Rat
- Oxidative Stress Is Not a Major Contributor to Somatic Mitochondrial DNA Mutations
- Molecular Identification of Collagen 17a1 as a Major Genetic Modifier of Laminin Gamma 2 Mutation-Induced Junctional Epidermolysis Bullosa in Mice
- Uncoupling of Molecular Maturation from Peripheral Target Innervation in Nociceptors Expressing a Chimeric TrkA/TrkC Receptor
- MicroRNAs Located in the Hox Gene Clusters Are Implicated in Huntington's Disease Pathogenesis
- Loss of Trabid, a New Negative Regulator of the Immune-Deficiency Pathway at the Level of TAK1, Reduces Life Span
- Targeted Ablation of Nesprin 1 and Nesprin 2 from Murine Myocardium Results in Cardiomyopathy, Altered Nuclear Morphology and Inhibition of the Biomechanical Gene Response
- Identification of Novel Genetic Loci Associated with Thyroid Peroxidase Antibodies and Clinical Thyroid Disease
- CEP-1, the p53 Homolog, Mediates Opposing Longevity Outcomes in Mitochondrial Electron Transport Chain Mutants
- Transcriptomics and Functional Genomics of ROS-Induced Cell Death Regulation by
- Quantitative Genome-Wide Genetic Interaction Screens Reveal Global Epistatic Relationships of Protein Complexes in
- Cascades of Genetic Instability Resulting from Compromised Break-Induced Replication
- Serine- and Threonine/Valine-Dependent Activation of PDK and Tor Orthologs Converge on Sch9 to Promote Aging
- Zfp322a Regulates Mouse ES Cell Pluripotency and Enhances Reprogramming Efficiency
- Insertional Mutagenesis and Deep Profiling Reveals Gene Hierarchies and a -Dependent Bottleneck in Lymphomagenesis
- DAAM Is Required for Thin Filament Formation and Sarcomerogenesis during Muscle Development in Drosophila
- Plasma Cholesterol–Induced Lesion Networks Activated before Regression of Early, Mature, and Advanced Atherosclerosis
- High-Resolution Profiling of Stationary-Phase Survival Reveals Yeast Longevity Factors and Their Genetic Interactions
- Comparative RNAi Screens in and Reveal the Impact of Developmental System Drift on Gene Function
- Accurate and Robust Genomic Prediction of Celiac Disease Using Statistical Learning
- Sex-Specific Embryonic Gene Expression in Species with Newly Evolved Sex Chromosomes
- Chromosome X-Wide Association Study Identifies Loci for Fasting Insulin and Height and Evidence for Incomplete Dosage Compensation
- Negative Feedback and Transcriptional Overshooting in a Regulatory Network for Horizontal Gene Transfer
- DNA Sequence Explains Seemingly Disordered Methylation Levels in Partially Methylated Domains of Mammalian Genomes
- Insights into the Genomic Landscape: Comparative Genomics Reveals Variations in Ploidy and Nutrient Utilisation Potential amongst Wine Isolates
- Molecular Evidence for the Inverse Comorbidity between Central Nervous System Disorders and Cancers Detected by Transcriptomic Meta-analyses
- The Centriolar Satellite Protein AZI1 Interacts with BBS4 and Regulates Ciliary Trafficking of the BBSome
- Fine-Mapping the Region Detects Common Variants Tagging a Rare Coding Allele: Evidence for Synthetic Association in Prostate Cancer
- Transmission Distortion Affecting Human Noncrossover but Not Crossover Recombination: A Hidden Source of Meiotic Drive
- A Variant in the Neuropeptide Receptor is a Major Determinant of Growth and Physiology
- Mutation of SLC35D3 Causes Metabolic Syndrome by Impairing Dopamine Signaling in Striatal D1 Neurons
- NSUN4 Is a Dual Function Mitochondrial Protein Required for Both Methylation of 12S rRNA and Coordination of Mitoribosomal Assembly
- MicroRNA-133 Inhibits Behavioral Aggregation by Controlling Dopamine Synthesis in Locusts
- Convergence of Light and ABA Signaling on the Promoter
- Arf4 Is Required for Mammalian Development but Dispensable for Ciliary Assembly
- Distinct Requirements for Cranial Ectoderm and Mesenchyme-Derived Wnts in Specification and Differentiation of Osteoblast and Dermal Progenitors
- Chk2 and P53 Regulate the Transmission of Healed Chromosomes in the Male Germline
- Ddc2 Mediates Mec1 Activation through a Ddc1- or Dpb11-Independent Mechanism
- Mapping the Fitness Landscape of Gene Expression Uncovers the Cause of Antagonism and Sign Epistasis between Adaptive Mutations
- Euchromatic Transposon Insertions Trigger Production of Novel Pi- and Endo-siRNAs at the Target Sites in the Germline
- miR-100 Induces Epithelial-Mesenchymal Transition but Suppresses Tumorigenesis, Migration and Invasion
- Canine Hereditary Ataxia in Old English Sheepdogs and Gordon Setters Is Associated with a Defect in the Autophagy Gene Encoding
- Within-Host Spatiotemporal Dynamics of Plant Virus Infection at the Cellular Level
- Analysis of Meiosis in SUN1 Deficient Mice Reveals a Distinct Role of SUN2 in Mammalian Meiotic LINC Complex Formation and Function
- Genome-Wide Association Study of Metabolic Traits Reveals Novel Gene-Metabolite-Disease Links
- Mechanistically Distinct Mouse Models for -Associated Retinopathy
- DAF-16/FoxO Directly Regulates an Atypical AMP-Activated Protein Kinase Gamma Isoform to Mediate the Effects of Insulin/IGF-1 Signaling on Aging in
- Chromosome I Controls Chromosome II Replication in
- Integrated Genomic Characterization Reveals Novel, Therapeutically Relevant Drug Targets in FGFR and EGFR Pathways in Sporadic Intrahepatic Cholangiocarcinoma
- The Iodotyrosine Deiodinase Ortholog SUP-18 Functions through a Conserved Channel SC-Box to Regulate the Muscle Two-Pore Domain Potassium Channel SUP-9
- The Genome of Highlights a Fish Pathogen Adapted to Fluctuating Environments
- Distinct DNA Binding Sites Contribute to the TCF Transcriptional Switch in and
- The Streamlined Genome of spp. Relative to Human Pathogenic Kinetoplastids Reveals a Parasite Tailored for Plants
- PLOS Genetics
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Genome-Wide Association Study of Metabolic Traits Reveals Novel Gene-Metabolite-Disease Links
- A Cohesin-Independent Role for NIPBL at Promoters Provides Insights in CdLS
- Classic Selective Sweeps Revealed by Massive Sequencing in Cattle
- Arf4 Is Required for Mammalian Development but Dispensable for Ciliary Assembly
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání






