-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaThe Systemic Imprint of Growth and Its Uses in Ecological (Meta)Genomics
Microbial minimal generation times range from a few minutes to several weeks. They are evolutionarily determined by variables such as environment stability, nutrient availability, and community diversity. Selection for fast growth adaptively imprints genomes, resulting in gene amplification, adapted chromosomal organization, and biased codon usage. We found that these growth-related traits in 214 species of bacteria and archaea are highly correlated, suggesting they all result from growth optimization. While modeling their association with maximal growth rates in view of synthetic biology applications, we observed that codon usage biases are better correlates of growth rates than any other trait, including rRNA copy number. Systematic deviations to our model reveal two distinct evolutionary processes. First, genome organization shows more evolutionary inertia than growth rates. This results in over-representation of growth-related traits in fast degrading genomes. Second, selection for these traits depends on optimal growth temperature: for similar generation times purifying selection is stronger in psychrophiles, intermediate in mesophiles, and lower in thermophiles. Using this information, we created a predictor of maximal growth rate adapted to small genome fragments. We applied it to three metagenomic environmental samples to show that a transiently rich environment, as the human gut, selects for fast-growers, that a toxic environment, as the acid mine biofilm, selects for low growth rates, whereas a diverse environment, like the soil, shows all ranges of growth rates. We also demonstrate that microbial colonizers of babies gut grow faster than stabilized human adults gut communities. In conclusion, we show that one can predict maximal growth rates from sequence data alone, and we propose that such information can be used to facilitate the manipulation of generation times. Our predictor allows inferring growth rates in the vast majority of uncultivable prokaryotes and paves the way to the understanding of community dynamics from metagenomic data.
Published in the journal: . PLoS Genet 6(1): e32767. doi:10.1371/journal.pgen.1000808
Category: Research Article
doi: https://doi.org/10.1371/journal.pgen.1000808Summary
Microbial minimal generation times range from a few minutes to several weeks. They are evolutionarily determined by variables such as environment stability, nutrient availability, and community diversity. Selection for fast growth adaptively imprints genomes, resulting in gene amplification, adapted chromosomal organization, and biased codon usage. We found that these growth-related traits in 214 species of bacteria and archaea are highly correlated, suggesting they all result from growth optimization. While modeling their association with maximal growth rates in view of synthetic biology applications, we observed that codon usage biases are better correlates of growth rates than any other trait, including rRNA copy number. Systematic deviations to our model reveal two distinct evolutionary processes. First, genome organization shows more evolutionary inertia than growth rates. This results in over-representation of growth-related traits in fast degrading genomes. Second, selection for these traits depends on optimal growth temperature: for similar generation times purifying selection is stronger in psychrophiles, intermediate in mesophiles, and lower in thermophiles. Using this information, we created a predictor of maximal growth rate adapted to small genome fragments. We applied it to three metagenomic environmental samples to show that a transiently rich environment, as the human gut, selects for fast-growers, that a toxic environment, as the acid mine biofilm, selects for low growth rates, whereas a diverse environment, like the soil, shows all ranges of growth rates. We also demonstrate that microbial colonizers of babies gut grow faster than stabilized human adults gut communities. In conclusion, we show that one can predict maximal growth rates from sequence data alone, and we propose that such information can be used to facilitate the manipulation of generation times. Our predictor allows inferring growth rates in the vast majority of uncultivable prokaryotes and paves the way to the understanding of community dynamics from metagenomic data.
Introduction
Maximal growth rates are central to microbial life-history strategies [1]–[9]. Among host-associated bacteria, competition often results in increased virulence through selection for higher growth rates as these have an outstanding role in the trade-off between rapid horizontal dissemination and slow clearance from the host [10],[11]. Highly infectious bacteria are associated with high maximal growth rates, e.g. enterobacteria, whereas bacteria producing chronic infections, e.g. mycobacteria, typically grow slowly under optimal conditions. The rapidity of spread of some bacteria poses a problem of urgency in antibiotic treatment, rendered more difficult by arising multiple resistances [12]. But slow growing bacteria sometimes also pose a therapeutic problem, as many antibiotics are ineffective in very slow growing cells [13]. Among free-living bacteria there is also a trade-off between fast growth in copiotrophs and scavenging potential in slow-growing oligotrophs [4],[14],[15]. Copiotrophic bacteria tend to have low affinity transporters and abundant gene expression machinery allowing fast growth in periods of feast, while enduring starvation in periods of famine where much of the protein synthesizing machinery is degraded [16]. Slow growing oligotrophs have high affinity transporters allowing them to thrive even under very small nutrient concentrations, but these become saturated or even toxic at high nutrient concentrations leading to their selective exclusion by fast growers in rich environments [17]. Because growth rates are outcomes and constraints of microbial life-history strategies, it is important to understand the mechanisms allowing fast growth and how they are imprinted by natural selection in genomes. Inversely, it would be extremely useful to predict maximal growth rates from sequence alone. This would allow establishing generation time predictions for the vast numbers of unknown or uncultivated bacteria for which we lack such information.
Classical studies in E. coli physiology have uncovered the physiological changes concomitant with fast growth (reviewed in [18]). When E. coli's generation time decreases from 100 to 24 min, cellular RNA polymerases (RNAP) are multiplied by 15 and ribosomes by 10. A large fraction of the additional transcription capacity is used to produce stable RNA (rRNA and tRNA). While the rate of synthesis also increases, it does so at much more moderate rates, e.g. elongation is faster by 40% for RNAP and 75% for ribosomes, which then attain maximal translation capacity. Thus, high growth rates result more from the increase in the production of the gene expression machinery than from its increasing productivity. At high growth rates, about 74% of all E. coli transcription concerns the production of stable RNA. To allow for such high levels of expression stable RNA genes tend to be in multiple copies in fast growing bacteria [19]. This multiplicity of rRNA operons constitutes a metabolic burden at lower growth rates [20].
In fast growing E. coli B/r, a replication round starts every 20 minutes, corresponding to the cell's minimal doubling time. Yet, replication of the chromosome takes ∼45 minutes [21]. This is possible because multiple rounds of replication can occur concurrently. The start of a new replication round before the previous one has finished doubles the number of regions around the replication origin in the cell. In cells with three simultaneous rounds of replication, genes the near the origin are thus 8 times more abundant in the cell than the genes near the terminus of replication. In the absence of negative feedback regulatory control, replication associated gene-dosage effects result in higher gene expression levels near the origin of replication [22]–[24]. Since genes coding for the translation and transcription machineries are under particularly strong demand at times of fast growth, there is a strong selection for their positioning near the origin of replication in fast growing, but much less so in slow growing, bacteria [25].
Even if tRNA concentration in the cell increases with growth rates, the tRNA/ribosome ratio decreases by 50% when comparing slow and fast growing E. coli [26]. The tRNA pool becomes limiting at very high growth rates. Thus, its quick turnover at ribosomes is under strong selection. This can be optimized if codons of highly expressed genes under fast growth recruit the most abundant tRNA in the cell [27]. Such codon usage bias, i.e. differential preference of some synonymous codons over others, is therefore as strong as the gene is highly expressed [28],[29]. It is also stronger for fast growing bacteria because of the above-mentioned decrease of tRNA/ribosome at higher growth rates and because in these conditions the few percent most highly expressed genes account for a larger fraction of all gene expression. Codon usage bias is thus thought to result from selection for accurate and fast translation by maximizing the recruitment of the most abundant tRNAs into ribosomes [30]. The highly significant role of translation and its machinery in the cell budget of fast growing bacteria makes codon usage bias a good predictor of gene expression levels under exponential growth [31],[32].
There have been studies on the association between maximal growth rates and rRNA operon [1],[19],[33],[34] and tRNA [35],[36] multiplicity, replication-associated gene dosage [25],[37] and codon usage biases [35],[38]. All these factors are thought to imprint genomes in accordance with the microbe's maximal growth rates. Previous studies focused on only one of the traits in one or few genomes and sometimes using coarsely binned growth data. To understand the relative role and importance of each factor and be able to manipulate growth rates more integrative studies are required. Unfortunately, the paucity of physiological data for the vast majority of microbes precludes the use of mechanistic models that can only be parameterized in E. coli [39]. Hence, we decided to use an empirical approach to answer the following questions: What is the association of each growth-related trait with maximal growth rates? How inter-correlated are they? What is their predictive power? Can we use the growth-related genomic traits to test ecological hypothesis with metagenomic data?
Results/Discussion
Genomic signatures of adaptation to fast growth
Following a previous work [35], we extracted from primary literature 214 minimal generation times (d) of species of bacteria and archaea (Table S1). We used this data to assess how genomic traits correlate with minimal generation times. We started by analyzing its correlation to genome size. Historically, microbial genomes have been viewed as short and compact due to selection for rapid replication and fast growth. In agreement with previous work [40],[41], we found no evidence for a positive correlation between minimal generation time and genome size or genome density (Spearman correlations ρ = −0.10 and −0.08, p-value = 0.13 and 0.24). The reasoning that smaller genomes allow for quicker replication is belied by the observation that replication can be initiated before the previous rounds have finished. There is thus no necessity for a direct correlation between genome size and minimal generation time, as observed.
As expected, we found an increase in copy number of rRNA (Figure 1) and tRNA genes (Figure S1) with decreasing minimal generation times (ρ = −0.59 and ρ = −0.51, all p-value<0.0001). The multiplicity of the subset of nearly ubiquitous tRNAs (ubi-tRNA, listed in Table S2), which in most species match the most favored codons [35], is more correlated with d than the other tRNA genes (ubi-tRNAs and non-ubi-tRNAs respectively, ρ = −0.54 and ρ = 0.13, p-value<0.0001 and p-value = 0.06, Figure S1). While many enterobacteria contain two copies of the highly expressed elongation factor Tu [42], we found no systematic trend for duplication of highly expressed protein coding genes in fast growers. Since each mRNA is translated ∼100 times [18], multiple copies of ribosomal protein coding genes would only be required to match the expression of rRNAs if the latter was present in excess of 100 copies. However, in our dataset, and in the rRNA Operon Copy Number Database [43], the maximal number of rRNA operon copies is 15 for Photobacterium profundum.
Fig. 1. Genomic signatures correlated to minimum generation time (d) for 214 prokaryotes. 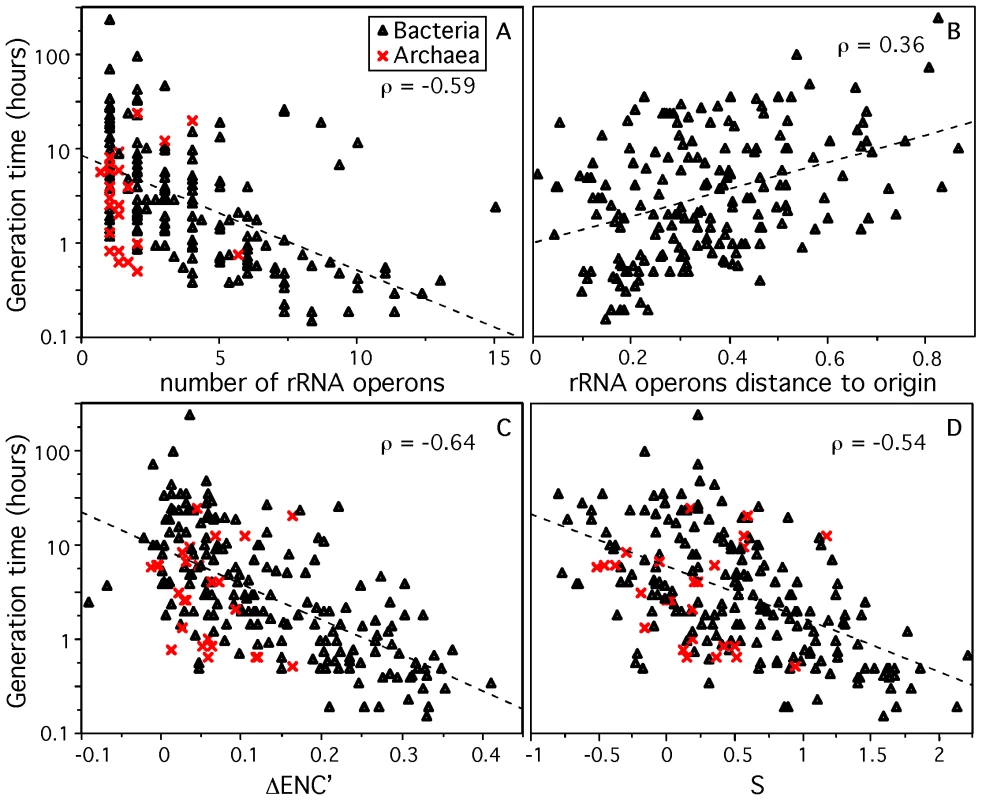
Correlation between d and (A) the number of rRNA operons in the genome, (B) the relative distance from the origin of replication to rRNA genes (excluding species with no retrievable origin), 0.5 corresponds to half the replicon, (C,D) codon usage bias indices ΔENC′ [35] and S [46]. Spearman correlations are given (ρ) with all p-values<0.0001. Dashed lines represent the trend of the correlation. As described above, gene dosage of highly expressed genes can be increased transiently when these genes are located near the origin of replication in fast growing cells. Indeed, a positive correlation was found between minimum generation time and the relative distance to the origin of replication of rRNA genes (ρ = 0.36, Figure 1), RNA polymerase genes (ρ = 0.42), ribosomal proteins coding genes (ρ = 0.42), tRNA (ρ = 0.35) and ubi-tRNA (ρ = 0.41) genes (Figure S2) (all p-values<0.0001). Hence, our data supports previous work suggesting that high growth rates are correlated with high transient or stable gene dosage in highly expressed genes associated with translation and transcription [25]. The importance of gene multiplicity, based on gene deletion studies, has been attributed to selection for quick start of exponential growth, not for its maintenance [1],[2],[19],[44]. These two effects are tangled in genome organization because selection for fast growth is usually associated with selection for quick start of exponential growth in copiotrophic bacteria enduring feast and famine regimes [1],[16],[45]. Once replication has started, the replication-associated gene dosage effect ensures that rRNAs are in much higher copy number in the cell than expected given their gene multiplicity. This makes the 7 copies of rRNA genes in E. coli to effectively increase in the cell by a factor of 5 under maximal growth [18]. Thus, gene multiplicity and replication-associated gene dosage can be seen as complementary, with the former being essential for the start of exponential growth and affecting stable RNA genes, and the latter ensuring high cellular concentration of translation and transcription-associated highly expressed genes under stable growth, thus affecting both RNA and protein coding genes.
Finally, two previously proposed indices of codon usage bias in highly expressed genes ΔENC′ [35] and S [46] correlate negatively with d (respectively, ρ = −0.64 and ρ = −0.54, p-value<0.0001, Figure 1). For the calculation of these indices we used the ribosomal proteins as the set of highly expressed genes under exponential growth (see Materials and Methods), as this is frequently done [29],[32],[35]. The ubiquity and high conservation of ribosomal proteins facilitate the identification of this set of genes in the subsequent metagenomic analyses. We tested that the results remained qualitatively similar when using other highly expressed genes under exponential growth, such as elongation factors or RNA polymerase genes (data not shown). Although ΔENC′ corrects for the influence of the G+C content of the genome on codon usage bias, we verified that G+C content is not correlated with minimal generation time (ρ = 0.06, p-value = 0.39) nor with ΔENC′ (ρ = 0.09, p-value = 0.24). Incidentally, genomic G+C content correlates with genome size (ρ = 0.61, p-value<0.0001) [47],[48]. The correlation between codon usage bias and minimum generation time is attributable to the selective pressure acting on highly expressed genes for the use of translationally optimal codons in these genomes where few genes correspond to the vast majority of gene expression. While experimental work has shown the advantages of optimizing codon usage bias for expression of heterologous proteins [49], our results suggest that optimization of highly expressed genes should lead to higher growth rates.
Phylogenetic dependencies between species may introduce a potentially important confounding factor in our analysis. If doubling times have important phylogenetic inertia then closely related genomes are bound to have similar growth rates and similarly important growth-related traits because their last common ancestor is too recent for these genomes to have diverged significantly. Hence, similarity in growth-related traits would not represent independent adaptive processes [50]. To test the effect of phylogenetic dependences we made an independent contrast analysis using a 16S-based phylogenetic tree (see Materials and Methods). All but one variable remained highly significantly correlated with minimal generation times after control for phylogenetic dependencies (Table 1). We have no explanation for the only exception, corresponding to the distance to the origin of replication of ubi-tRNA genes. We then analyzed how the difference in minimal generation times between two genomes increased with evolutionary distance (Figure 2A). This shows that when genomes are distant more than 0.2 substitutions/nt in our alignment there is no correlation between the two variables. Less than 8% of all pairs of genomes are distant by less than this threshold distance. This shows that evolutionary inertia on minimal growth rates is indeed low, often limited to the genera. We then performed the same analysis for all other variables (Figure 2B). This shows that even at low evolutionary distances, the minimal generation time has the lowest evolutionary inertia. It is thus tempting to speculate that changes in minimal growth rates tend to pre-date changes in growth-related traits, and not the other way around.
Fig. 2. Relative difference between the minimum generation time, codon usage bias indices, and G+C content of pairs of organisms and their phylogenetic distance for 214 prokaryotes. 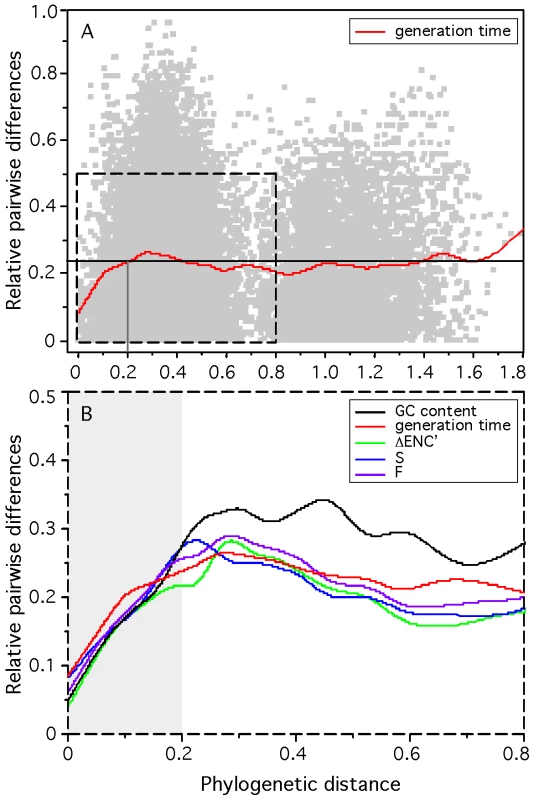
Pairwise phylogenetic distances were computed from the matrix of the phylogenetic tree reconstruction (see Materials and Methods: phylogenetic analysis). Pairwise differences in doubling times (box-cox transform of d), codon usage bias indices ΔENC′, S and F and G+C content were normalized by the maximum observed difference in the 22791 pairs dataset (eq. 10). (A) The datapoints are represented in light gray. The red line represents a flexible spline fit (λ = 0.01). The black horizontal line represents the average relative pairwise difference. (B) The lines represent a flexible spline fit (λ = 0.01). For short distances (light gray area), the spearman correlations between phylogenetic distance and the relative difference in minimal generation times, ΔENC′, S and F and G+C content are respectively: 0.21, 0.28, 0.28, 0.29, 0.26 (all p-values<0.0001). Tab. 1. Most informative attributes for the prediction of minimum generation time. 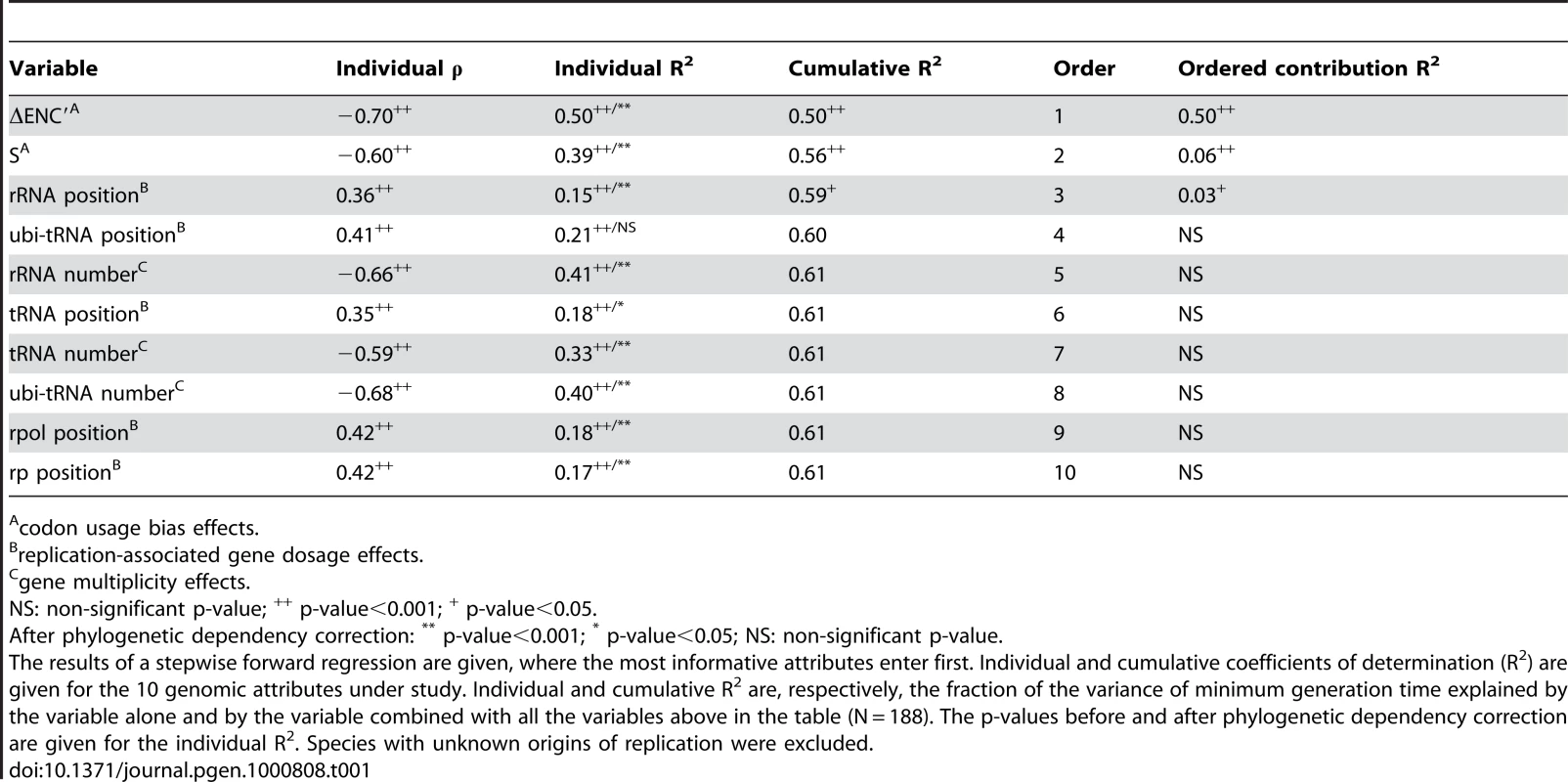
codon usage bias effects. In summary, low minimal generation times are associated with the optimization of the translation machinery through: codon usage bias, an increased number of rRNA and tRNA gene copies by gene amplification, and the transient replication associated gene dosage of highly expressed genes under exponential growth. This information could be useful to reprogram growth rates in prokaryotes by synthetic biology approaches because modification of these traits should modify minimal generation times. Indeed, lower growth rates result from deletion of rRNA operons and from inversions decreasing gene dosage effects [19],[51]. Similarly, lower codon usage bias leads to lower growth rates in viruses [52]. Naturally, not all traits are equally easy to manipulate. While insertions of extra rRNA operons, e.g. using plasmids, are relatively straightforward, extensive changes in codon usage bias are only viable if the whole sequence is synthesized in vitro. This is now possible for viruses and even small bacterial genomes [53],[54].
Codon usage bias is the best determinant of minimum generation time
Having delimited a range of 10 variables that correlate significantly with maximal growth rates (column Individual R2 in Table 1), we estimated their predictive power using stepwise forward regressions. This allows to iteratively introduce in the model the most contributing variables while minimizing the number of variables in the model by excluding the ones without significant explanatory power [55]. For this analysis, we only used the 188 species for which we could retrieve an origin of replication (out of 214). To normalize the data we used a box-cox transformation Φλ(d), which in this case approximates to the commonly used log-transformation (Figure S3). We focused on the increase in explained variance given by the inclusion of each variable (column Cumulative R2 in Table 1). The highest contributing variables are ΔENC′, S and the relative distance of the rRNA genes to the origin of replication (R2 contribution column in Table 1). Prokaryotic genes often cluster in operons. We therefore tested if there were changes in the results if we had used operons instead of genes. We did this in the most significant positional variable, rDNA, and found no differences in the correlation with doubling time (ρ = 0.37 for genes and ρ = 0.36 for operons, both p-values<0.0001). Although rRNA operon multiplicity has a high individual explanatory power, it doesn't add new information into the model when codon usage bias, which has higher explanatory power, is already included. Hence, adaptation to fast growth is very strongly correlated in terms of gene multiplicity and codon usage bias, possibly because both are essentially associated with the optimization of translation. Genome organization around the origin of replication is less correlated with codon usage bias, possibly because it reflects the impact of replication rates on transcription: faster DNA polymerases lead to lower gene dosage effects for a similar generation time.
We then tested if the phylogenetic information could be a good predictor of minimal generation times. For this we made a stepwise regression where we added one more variable: the generation time of the most closely related genome. This variable adds little additional information (R2 = 0.65 versus R2 = 0.61 without the variable). The first variable to enter in the stepwise regression is still ΔENC′ (Table S3). This result is consistent with the abovementioned low phylogenetic inertia of minimal generation times. Since phylogenetic information is not as amenable to mechanistic interpretation as the other variables we didn't include it in the final predictor.
ΔENC′ and S both measure the intensity of selection for optimization of the translation of highly expressed genes. However, because they do it differently they both carry significant predictive power. These are the only genomic traits mentioned above that can be calculated from partial genome sequences, an undeniable advantage for the construction of a sequence-based predictor of minimum generation time. Evaluation of the codon usage bias does not require prior knowledge about the origin of replication, we can thus build our predictor on the full dataset (N = 214).
Since together ΔENC′ and S have larger explanatory power than individually (R2ΔENC′ = 0.44, R2S = 0.33, R2both = 0.49, p-value<0.0001), we combined them using principal component analysis. The first component, explaining 47% of the variance of minimum generation times, was called F (ρ = −0.66, p-value<0.0001). A preliminary linear predictor of Φλ(d) in function of F was obtained by a least squares regression (N = 214, R2 = 0.47):(1)
Fast growth while coping with extreme temperatures
The fit of the model showed that psychrophiles and thermophiles are systematically grouped above and below the prediction line, respectively (Figure 3). This suggests that part of the deviation from the model is biologically relevant and not a mere product of poor modeling or measurement errors. The residuals of the regression, representing the deviations to the model, are negatively correlated with optimal growth temperature (ρ = −0.37, p-value<0.0001, Figure 4). Naturally, we used minimal generation times obtained at optimal growth temperatures, therefore this result does not reflect slower growth at low temperatures of species with higher optimal growth temperature. This is also not an indication of higher growth rates at optimal growth temperatures in thermophiles. In fact, there is no significant difference of minimal generation times between thermophiles, mesophiles and psychrophiles (p-value>0.05 for ANOVA and Wilcoxon tests). This is also not caused by the over-representation of archaea among thermophiles, since archaea and bacteria do not have significantly different deviations to the model (p-value>0.1, Wilcoxon test). The association between deviations to the model and optimal growth temperature indicates that psychrophiles (thermophiles) are slower (faster) growers than expected given their genome growth-associated traits. While the above residuals are from a regression where only codon usage bias was used, we found similar patterns while analyzing the residuals of regressions using only information on gene multiplicity or replication associated gene dosage effects (data not shown). Hence, the association of deviations of the growth-related traits with optimal growth temperature is not exclusive to codon usage bias. Since there are no differences in minimal generation times between the different groups this suggests that for a given minimal generation time the psychrophiles require more structured genomes than mesophiles and these more than thermophiles.
Fig. 3. Minimum generation time (d) versus codon usage bias for 214 prokaryotes. 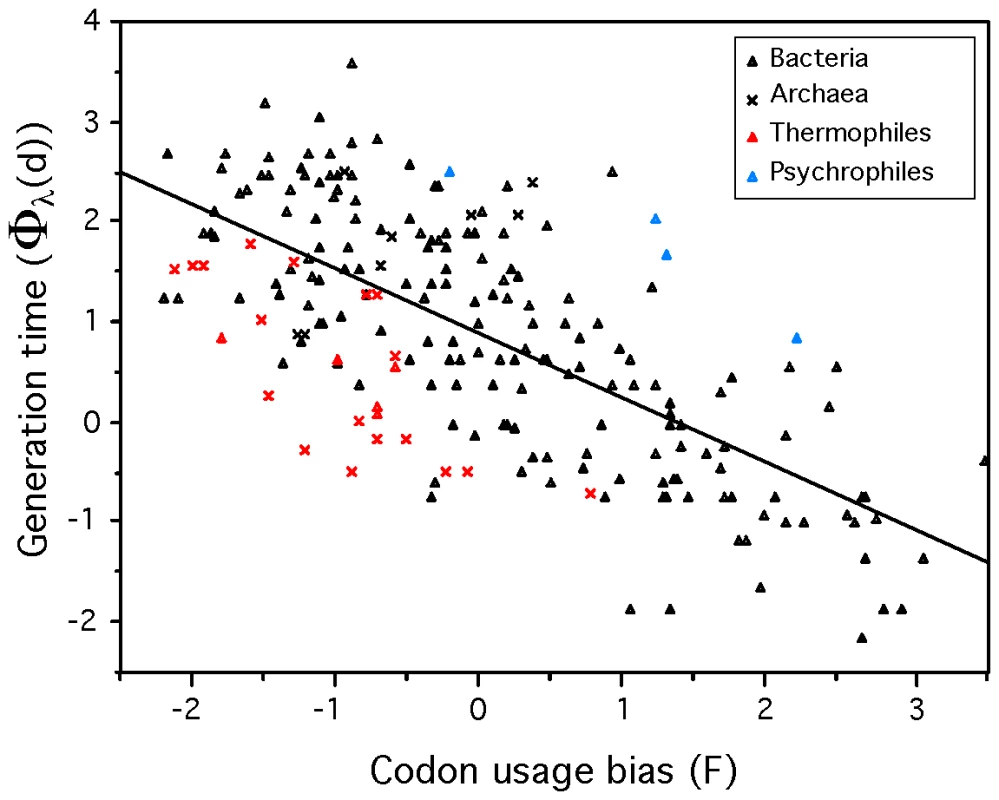
F (first principal component of ΔENC′ and S) and Φλ(d) (Box-Cox transform of d) are negatively correlated (ρ = −0.66). Line fitted by least squares regression: Φλ(d) = 0.8741−0.6496 F (R2 = 0.47, p-value<0.0001). Fig. 4. Correlation between the residuals of the model (eq. 1) and optimal growth temperature (OGT). 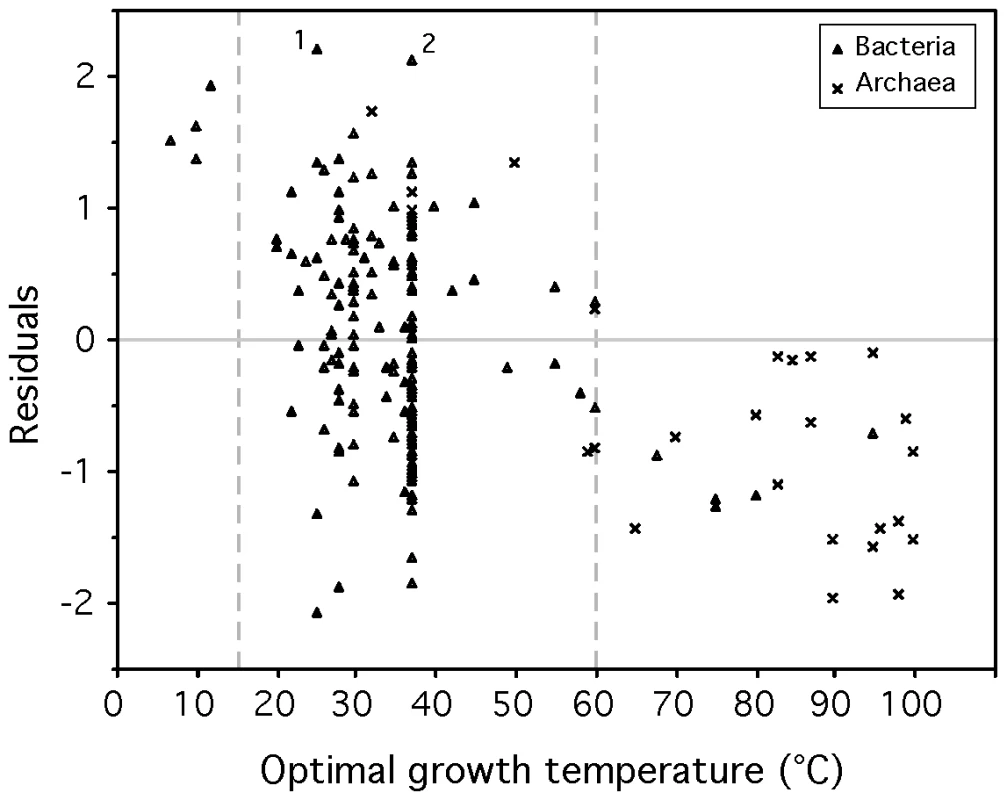
Sperman correlation ρ = −0.37, p-value<0.0001. Residuals are positive for psychrophiles (OGT<15°C) and negative for thermophiles (OGT>60°C), indicating that for the former (latter) the observed minimal generation time is lower (higher) than expected from the genomic signatures. Relevant outliers: 1Sodalis glossinidius morsitans and 2Mycobacterium leprae. Fast-growth associated traits are probably under weak selection, therefore subject to mutation-selection-drift balance. These results could then be interpreted as a sign of negative temperature dependence of selection for growth-related traits. At high temperature there would be less selection for optimization of these traits than at lower temperatures. Accordingly, mutations disrupting these traits are under strong purifying selection in psychrophiles and relaxed selection in thermophiles. For example, Desulfotalea psychrophila, Methylobacillus flagellatus and Pyrococcus furiosus present very similar genomic trends of adaptation to a minimum generation time of ∼3 hours (F = −0.23, −0.20 and −0.25 respectively). However, their respective observed minimum generation times are of 27, 2 and 0.6 hours for optimal growth temperatures of 7, 36 and 100°C.
The temperature dependence of the deviations to the model could also result from differences in effective population sizes in the different groups, if effective population size decreases with optimal growth temperature. We don't have data allowing the test of such a hypothesis. Instead, it is tempting to associate the effect of optimal growth temperature on the degree of genome optimization for fast growth with the dependence of enzymatic activity on temperature. At higher temperatures diffusion increases, water viscosity and activation energy decrease, facilitating rapid reactions [56] and could thus lead to lower requirements for growth-associated traits. As a case in point, psychrophiles have the highest multiplicity of rRNA and tRNA genes [57], whereas even fast-growing thermophiles have few copies, with a maximum of 4 rRNA operons in Thermoanaerobacter tengcongensis and Carboxydothermus hydrogenoformans. High temperatures possibly increase the catalytic rates of translation-associated reactions, and also the tRNA diffusion into ribosomes, allowing quick start and maintenance of exponential growth with fewer genes. This leads to weaker selection for gene multiplicity, lower codon usage bias and lower replication associated gene dosage effects. Hence, while we find no evidence that psychrophiles grow slower than other prokaryotes, they do show a tendency to strongly select for growth-related traits.
After derivation, our predictor of minimal generation times (d in hours) (N = 214, R2 = 0.58) including optimal growth temperature (OGT in °C) becomes:(2)See Materials and Methods for a detailed derivation of the equations. For mesophilic organisms this simplifies to (N = 187, R2 = 0.59, Figure 5):(3)We made a program to compute the expected minimal generation time given sequences of highly expressed genes and other genes in genomes. The program is publicly available at http://mobyle.pasteur.fr/cgi-bin/portal.py?form=growthpred. The information on ribosomal proteins for all the genomes and metagenomes used in this work can be found at the same site.
Fig. 5. Observed versus predicted minimum generation time. 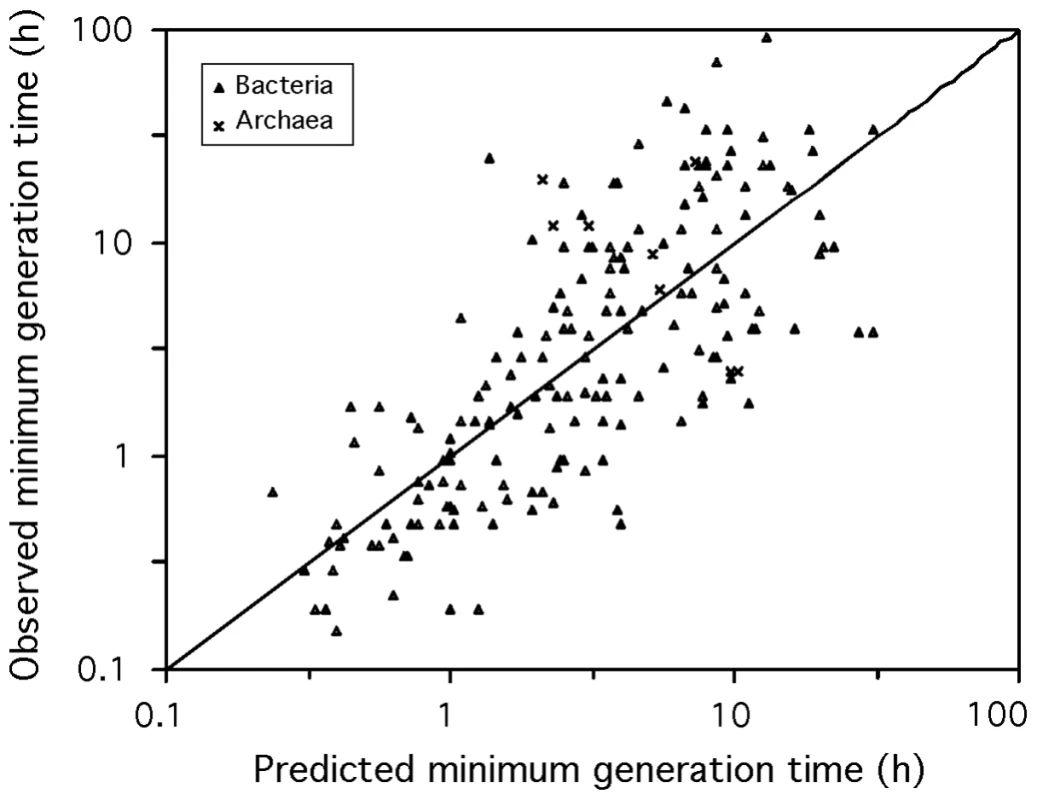
The mesophilic predictor based on codon usage bias (eq. 3) was applied to the 187 mesophilic prokaryotic genomes. The diagonal black line corresponds to the identity. Evolution of growth rate traits during genome reduction
We next investigated the genomes of mesophiles deviating most from the model. The highest positive residuals, corresponding to genomes with lower than expected maximal growth rates, are from the genomes of Sodalis glossinidius morsitans and Mycobacterium leprae, with observed generation times ∼18 and 35 times slower than expected. These genomes have the highest number of pseudo-genes within our data set (respectively, 49% and 50% of non-coding DNA), resulting from an ongoing process of genome reduction [58],[59]. It has been estimated that pseudogenes in M. leprae have an average age of ∼9 million years and have accumulated ∼15% of changes since then [60]. Naturally, synonymous positions of functional genes should evolve at least as slowly. Thus, even if selection for biased codon usage decreases, the slow pace of accumulation of synonymous substitutions by drift takes a long time to lower the bias down in highly expressed genes to the new value expected by the mutation-selection equilibrium for the new maximal growth rate. The lower phylogenetic inertia of minimal generation times, compared with other traits, namely codon usage bias (Figure 2B), justifies why the highest positive residues are among the genomes that have higher pseudogene density, in agreement with suggestions of a recent dramatic shift in lifestyle. Indeed, S. glossinidius and M. leprae grow much slower than the other closely related mycobacteria and free-living enterobacteria [61],[62]. Genomes that have endured slow growth for a long period of time such as Buchnera aphidicola, Rickettsia typhi or Mycoplasma pneumoniae have now lost any putative ancient organization related to high growth rates. These genomes thus conform to the predictions of maximal growth rates based on genome analysis.
Prediction of growth rates from partial data
We adapted the codon usage bias indices to make them computable from partial genomic and metagenomic data (see Materials and Methods). Measuring these variables on small sets of genes inevitably introduces some uncertainty in the estimation of the parameters. To evaluate the associated error, we sampled sets of genes of varying cardinality from mesophilic genomes for which we know the doubling time. We did this for non-highly expressed genes comparing them with the whole dataset of highly expressed genes (HEG), and inversely. The resulting ΔENC′ and S values were then subject to principal components analysis, of which the first component (Fa) was compared with the one obtained from the whole genome. The results for 3 organisms (fast, slow and intermediate growers) are represented in Figure 6 for the first set of experiments and in Figure S4 for the latter. As expected, the estimates of Fa are less accurate with decreasing sample size. We then varied the sample size of both populations of genes and found that the analysis still had a remarkable power even when considering only 5 highly expressed and 5 non-highly expressed genes. In this case, a discrete classification of the mesophilic species (see Materials and Methods) into very fast, fast, intermediate and slow resulted in 50% exact classifications (expected 25%) and 89% approximate or exact classifications (prediction matching the same observed class or the adjacent ones, expected 59%). Even in this extremely small set of 10 genes, we only found 7% of slow growers predicted as fast or very fast or vice-versa (expected 29%). Therefore, a robust coarse qualitative assessment of minimal generation times can be made even with as few as ten genes (see Table S4 for a comparison of the results of discrete classification with the total set of genes, 40 genes, 20 genes and 10 genes). Such genome samples are easily accessible in metagenomic data from low diversity environments. For the other environments, the increase in coverage or the use of large-insert bacterial artificial chromosome libraries will also produce sufficiently large contigs [63].
Fig. 6. Accuracy of the determination of composite codon usage bias (Fa.) with varying sample size. 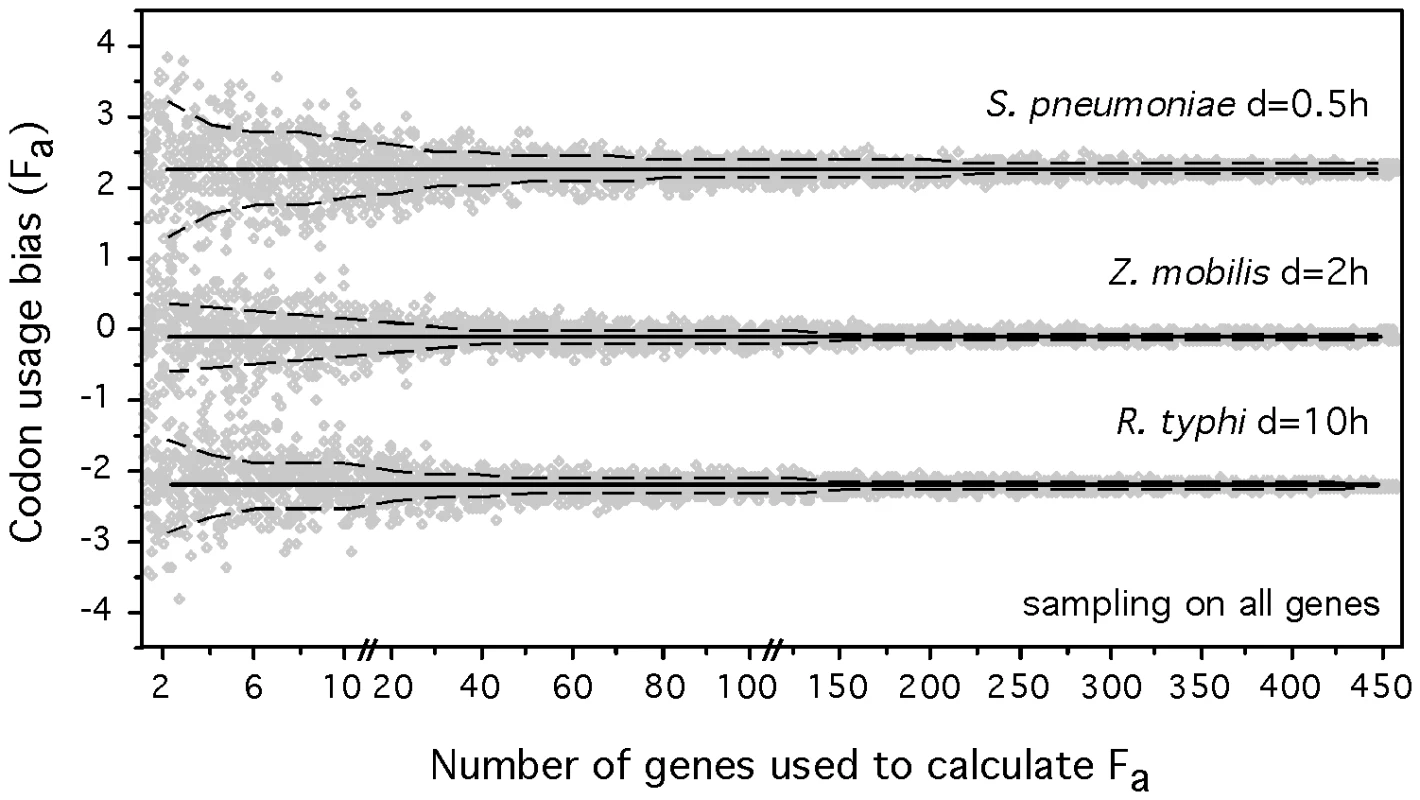
Fa was calculated on randomly chosen samples (from 2 up to 450 genes) of all genes while using the full dataset of highly expressed genes. 100 iterations were effectuated for each sample size. The results for 3 organisms (one fast, slow and intermediate grower) are represented. The full black lines correspond to the whole genome value of F and the dashed lines to the standard deviations. Each data point is represented in gray. Prediction of growth rates in prokaryotic communities
Given the possibility of inferring minimum generation times from partial genomic data, we selected published metagenomic datasets to test 2 hypotheses: First, that environmental factors such as presence of toxic contaminants or resource availability influences the growth rate strategies of the resident microbial populations. Second, that fast growers are favored during the colonization phase of a new niche.
Environmental samples can be interpreted either as collections of pseudo-genomes or as metagenomes. In the former approach sequences putatively assigned to one same species can be put together in pseudo-genomes. In this approach, a large fraction of the data is lost because most species genomes are not sequenced and because genomes are so diverse in terms of gene repertoires that some genes will not match a template genome of the same species [64]. This approach has the advantage that if species are well known we can make more informed interpretations and we can control for phylogenetic dependencies. In the latter approach the sequences are all put together and treated as a great single meta-genome. This has the advantage of using all the data, including all the elusive non-cultivated prokaryotes, and accounts for the different availability of different species by their different quantitative contributions to the sample. However, it does not allow controlling for phylogenetic dependencies. We have preferred to use the second approach because we wanted to account for uncultivated species and relative frequencies of each species. We then confirm the results using the first approach.
Growth rate strategies in different environments
We first used our partial genomic data predictor on 3 datasets corresponding to very different environments for which simple predictions of maximal growth rates could be made: the human distal gut microbiome [65], the Waseca county farm soil metagenome [66] and the acid mine drainage biofilm metagenome [67] (for details of each dataset, see Tables S5 and S6). The human gut is a very rich environment, with periodic high nutrient inflow and with an important wash out rate to a poor outside environment. As a result, bacteria proliferating in the gut are subject to a feast-and-famine lifestyle, which has been proposed to select for very high growth rates [16],[68]. On the other extreme, the acid mine drainage biofilm reflects adaptation to a stable, nutrient poor and extremely toxic environment. In this situation one expects to find organisms that grow slowly but have great capacity to withstand stressful conditions [69]. The farm soil is an intermediate environment, where all the array of growth rates might be found, reflecting different life strategies (colonizers, stress resistant, capable competitors, etc) [70]. We therefore expected to find low average minimal generation times in the gut, intermediate in the soil and high in the acid mine drainage biofilm.
Each metagenome was processed to obtain gene sequences large enough to allow meaningful measures of codon usage bias (see Materials and Methods). We then used the predictor for mesophiles (equation 3) to obtain average minimum generation times for each set. We found that the predicted average minimum generation times were of 1.8h (human gut), 4.6h (farm soil) and 10.2h (acid drainage) (Figure 7). These differences are highly significant as computed by bootstrap sampling on genes in the datasets (p-value<0.001 for details see Materials and Methods: Bootstrap on metagenomes). These samples were taken in environments with different temperatures. Since we showed that optimal growth temperature affects the predicted generation times, we repeated the analysis controlling for this effect. For this we used the average optimal growth temperature of the pseudo-genomes found in the sample (see below; 40°C for the acid mine, 30°C for the farm soil and 37°C for the human gut). The differences between the datasets remain significant after this control (p-value<0.001). This shows that our method gives results matching our expectations in that the human gut selects for fast-growers while toxic environments do not.
Fig. 7. Average predicted minimum generation time for 3 environmental metagenomes. 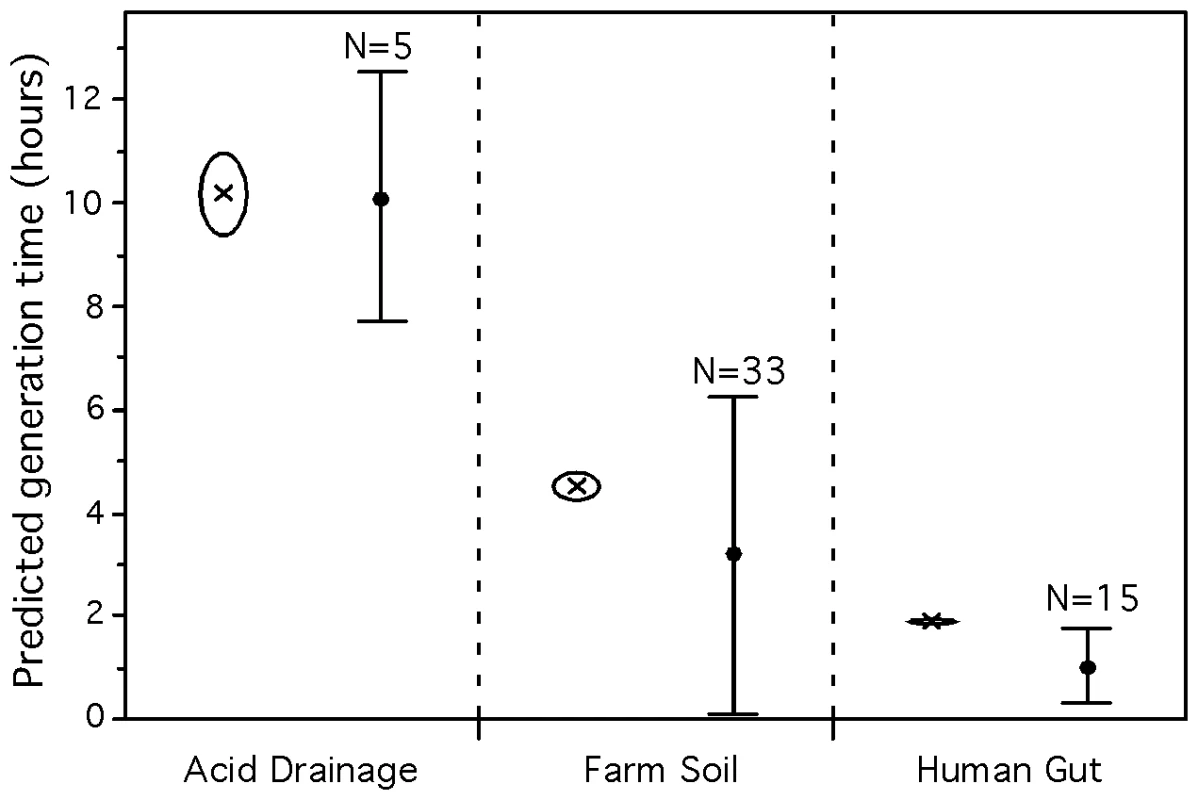
Crosses represent the average for the whole metagenome approach while dots represent the average for the pseudo-genome approach. All predictions were calculated with the predictor for mesophilic organisms (eq. 3). The average minimum generation time of the whole metagenome (crosses) and the respective standard deviation (open circles) were generated with 1,000 bootstraps on the dataset of all genes and highly expressed genes independently. The 3 whole-metagenome datasets are all significantly different (p-value<0.001). Minimum generation times were calculated using the whole genome of the sequenced genomes matching proteins of the metagenome (see Materials and Methods: classification of metagenomes into pseudo-genomes). The number of matching sequenced genomes are given above the average (dots) and standard deviation (bars) of the predictions. The 3 pseudo-genomes datasets are all significantly different (Tukey-Kramer: p-value<0.05). It is interesting to compare these growth rates with bacteria that are known to be part of these communities. In the human gut, clostridia, bacteroides and enterobacteria constitute a significant fraction of the community and by far the best studied one. Representative species such as E. coli, E. faecalis, L. johnsonii and C. perfringens have doubling times smaller than the community average of 1.8h (0.4h, 0.5h, 0.9h and 0.2h, respectively) and whole genome prediction of doubling times in conformity (0.8h, 0.7h, 0.6h and 0.4h). However, the predominant species in healthy adults, Bacteroides thetaiotaomicron, has an observed minimum generation time (1.5h) smaller than what is expected by its growth-associated genomic traits (3.4h). Again, typical soil bacteria, such as the Streptomyces or the alpha-proteobacteria, tend to have doubling times lower than the community average of 4.6h. Yet, they have generation times higher than the above-mentioned bacteria from the human gut, e.g. 2.2h for Streptomyces coelicolor, 2.4h for Mesorhizobium loti and 8h for Nitrobacter winogradskyi, with predictions 2.1h, 3.0h and 6.0h, respectively. In the acid mine drainage biofilm there are very few species, thus the scaffolds available correspond to almost complete genomes. These include two species for which generation times have been experimentally evaluated: Ferroplasma acidarmanus Type I with d = 4h [71] and Leptospirillum sp. Group II with d = 12h [72]. These observed values are close to the obtained by our predictions 6h and 13h respectively, using the scaffolds.
The lag between the growth rates of the best-studied bacteria of the human gut and farm soil and our metagenomics results could be due to a bias in our method. However, the analysis above shows that while smaller sequences reduce the accuracy of the estimates they do not seem to bias them in a given direction. It may thus be that the gap underlies a biological cause, the heterogeneity of these systems and the bias of cultivable organisms. Adhesion to the gut wall in biofilms and persistence in the soil under intense competition favors slower growth rates. Yet, cultivation methods will favor the isolation of fast growers. In order to further detail the metagenomic datasets in terms of the variance of its constituents, we classified the metagenomic proteins into pseudo-genomes (see Materials and Methods and details in Table S7). 11% of the proteins of the human gut microbiome matched 15 sequenced genomes, while 0.05% of the farm soil proteins matched 33 sequenced genomes. This shows that approaches based on aggregating sequences around pseudo-genomes ignore the majority of the data. Importantly, these results suggest a higher biodiversity in the farm soil than in the human gut, as expected, and it demonstrates that most of it is not represented in the sequenced genomes available to date. We then computed the predicted minimum doubling times for the matching sequenced genomes (using the whole genomes) and for the large scaffolds available for the 5 species present in the acid mine biofilm. The average minimal doubling times of the 3 environments are still significantly different (Tukey-Kramer: p-value<0.05). The results show that the human gut presents clearly the lowest variance in minimal doubling times. This is in agreement with a high selection pressure for fast growers in the human gut. On the other hand, the farm soil environment presents the highest variance (Figure 7), suggesting the coexistence of microorganisms with different life-strategies. Furthermore, as a control for possible phylogenetic dependencies, we repeated the analysis using one species per genera in each environment. The results remain significant (Tukey-Kramer: p-value<0.05). Hence, the pseudo-genome approach allows the analysis of the environment diversity in terms of growth rates and matches the expectation that highly toxic and very nutrient rich environments are less diverse in this respect.
Ecological succession in the human gut
The gastrointestinal tract of a healthy fetus in utero is sterile. Microorganisms from the mother and the surrounding environment are acquired during the birth process and thereafter through breast-feeding and social interaction. However, not all of them will succeed in colonizing the gastrointestinal tract. The gut microbial community is initially dominated by enterobacteria and streptococci, with subsequent establishment of the anaerobic Bacteroides, Clostridium and Bifidobacterium. The latter clearly dominating for the entire breast-feeding period [73]. As solid diet is introduced, a more complex and dense gut ecosystem will develop and eventually reach a dynamical balance with its host. The first phase of this microbial succession, corresponding to the colonization of the nutrient-rich gut, should be dominated by faster growing organisms. This corresponds to the classical prediction in evolutionary ecology that colonizers are in general fast-growers [74]. To test it, we used our partial genomic data predictor on the gut microbiome of several adults, weaned children and unweaned babies [75]. The latter represent the niche under colonization. Indeed the gut metagenome of unweaned babies (prediction 1.4h) have significantly lower average minimum generation time than those of children (2.4h) and adults (2.4h) (ANOVA: R2 = 0.84, p-value<0.0001, Figure 8). The results are identical for adults and young children (1.5 and 3 years old), which suggests a rapid evolution of the gut microflora after diet alteration.
Fig. 8. Average predicted minimum generation time for the gut metagenomes of humans of different age groups. 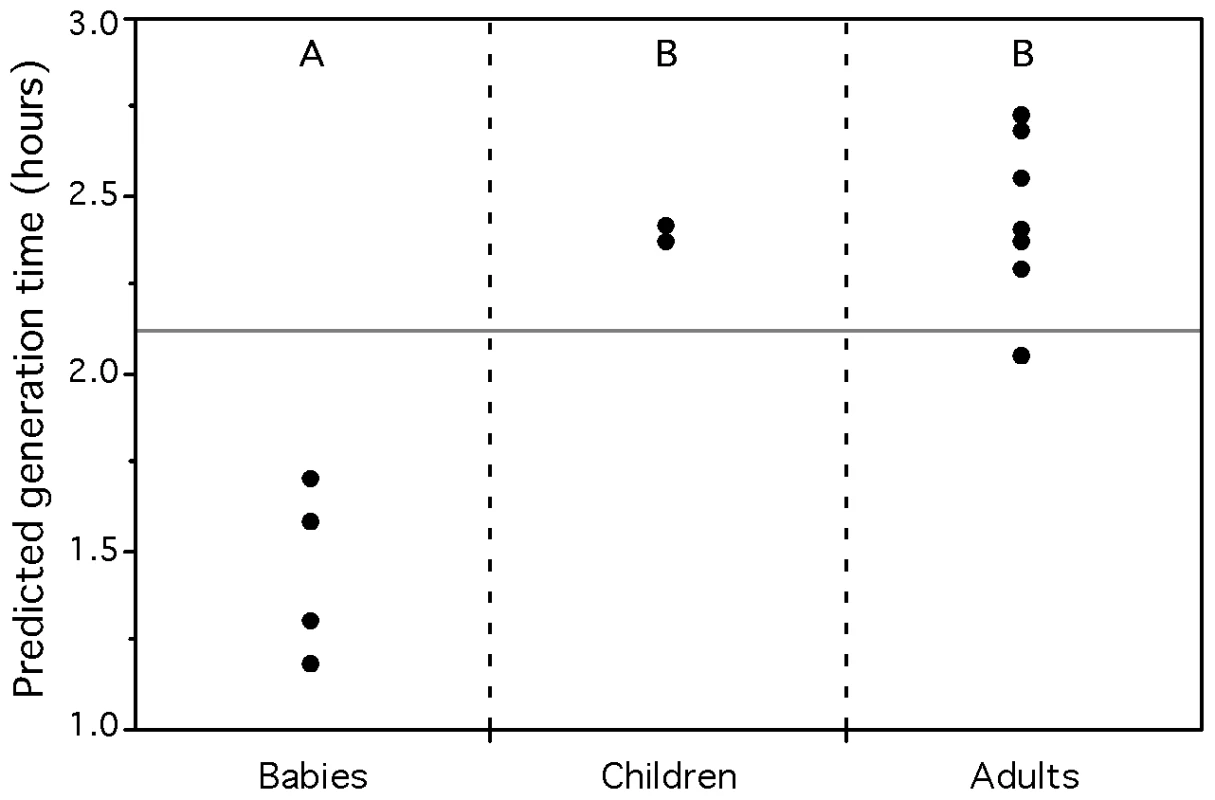
Unweaned babies are 3, 4, 6, and 7 months old. Weaned children are 1.5 and 3 years old. Adults are between 24 and 45 years old. Groups not connected by the same letter (A or B) are significantly different (Tukey-Kramer: p-value<0.005). The full horizontal line represents the average of the predictions for all individuals. It is also interesting to notice the difference between the Japanese and American gut metagenomes. No Bacteroides 16S rRNA genes were found in the American dataset, although other studies confirm that Bacteroides are predominant in the human gut microbiota [76],[77]. This discrepancy was identified by the authors and attributed to possible complications in the DNA extractions [65]. However, such complex protocols might induce other sampling biases, harder to detect. Thus, one must be cautious when comparing metagenomes from different projects/laboratories. Nevertheless, the average minimum generation times of the 4 Japanese babies remain significantly lower than those of the two American adults (ANOVA: R2 = 0.70, p-value = 0.02).
We also classified the metagenomic proteins of the Japanese gut microbiomes into pseudo-genomes and calculated predicted minimum generation times based on the matching whole genome sequences. 11% of the proteins of the gut microbiomes matched sequenced genomes. The average number of species found in the different age groups' microbiota are not significantly different (26 for babies, 26 for children and 22 for adults, Wilcoxon: p-value = 0.64). We analyzed the groups' doubling times in 3 different ways, in order to compare them to the results of the whole metagenome analysis (Table S8). First, there is no significant difference in the arithmetic average of the predictions for the babies, children and adults. However, if we weight the contribution of the value of each pseudo-genome by the number of proteins of the metagenome that matched it, then we recover a result close to the one of the whole metagenome, where unweaned babies have a significantly lower average minimal generation time than children and adults (Tukey-Kramer: p-value<0.01). We find similar results when keeping only one species per genera (Table S8). Therefore, we find no evidence that the gut microbiota of adults is composed of slower growing species than the one of babies. Instead, the relative abundance of species in the gut population accounts for faster growing communities in babies. This highlights the interest of the whole metagenome approach, which intrinsically takes into account this information.
Concluding remarks
Our results show that minimal generation times imprint genome organization and sequence of Bacteria and Archaea. They also show that such information allows the prediction of maximal growth rates from sequence alone. Naturally, organisms rarely grow at maximal growth rates because they rarely meet ideal growth conditions. As a result, our data does not allow predicting growth rates in specific environments. Yet, information on the maximal growth rates coupled with biochemical modeling can eventually lead to prediction of growth rates in particular media [78]. The optimization of growth related traits allows the quick start of exponential growth upon favorable environmental changes and allows faster growth also under sub-optimal conditions. In this sense, maximal growth rates are proxies of the capacity of the species to rapidly produce biomass, to quickly change growth rates and to take advantage of rich media. If such traits were not important, then random mutations erasing codon usage bias, genome organization and gene multiplicity would not be selected against and none of these traits would be found. Instead, we have shown that the majority of genomic traits that correlate significantly with maximal growth rates are also strongly correlated among themselves. This is a consequence of a shared selective pressure leading to the adaptation of the cellular machinery for high growth potential.
We found that some unexpected variables have strong influence in genome optimization for growth, notably ongoing genome reduction and optimal growth temperature. The slow pace of substitutions is likely to explain the higher than expected codon usage bias in reducing genomes. The association of optimal growth temperature with deviations to expected growth rates might result from the enzymatic rate dependence on temperature, but that remains openly speculative until comparative data on the translation biochemistry of psychrophiles and thermophiles becomes available. Other variables may also influence maximal growth rates and genome optimization. We detail three types. First, while we made exhaustive searches in primary literature to collect minimal generation times, there is substantial incertitude on these. We may have missed some publications with lower generation times, but more importantly, current growth conditions are still far from optimal for many prokaryotes. This introduces a bias in the analysis, since slow-growers are much less studied than fast-growers. For example, a search in the PubMed database of the number of articles citing each of the species we analyzed showed that this number is highly correlated with the minimal generation times (ρ = −0.45, p-value<0.0001). Hopefully, our data will be of use to pinpoint the species for which a revision of growth times will be most likely to be fruitful, since the largest residuals that are not explained by temperature or ongoing genome reduction might concern prokaryotes for which generation times are less accurate. Secondly, other measures of within genome bias in gene expression such as strength of ribosome binding sites, promoters, operon organization and genome structure might improve our predictor [79]–[82]. Yet, since our 10 growth-associated traits were all highly correlated, increasing the number of growth-associated traits in the analysis is unlikely to add much information. Thirdly, environmental variables that can affect growth can have more important, and for the moment unforeseeable roles, especially if they affect enzymatic activity. As the database grows larger we will be able to better pinpoint them by systematic analysis of deviations from the predicted values, as we found for optimal growth temperature.
Along the discussion of our results we have systematically interpreted deviations from the model in a selective perspective. This is based on the extensive literature showing the physiological effects of selection for growth-related traits in exponentially growing cells. Yet, most growth related traits, e.g. codon usage bias, are expected to be under weak selection thus liable to genetic drift depending on the effective population size (Ne). If Ne is independent of maximal growth rates this will only result in increased variance in our predictor. But if Ne is negatively correlated with minimal generation times then fastest growing organisms could have more growth-related traits than slow growers because of higher selection coefficient for these traits and/or because of more efficient selection, ie higher Ne. In this case, our predictor for growth rates would also be a predictor of effective population size. While selection for growth related traits is not under dispute, systematic deviations from the model could be strongly influenced by the effective population size. For example, if Ne were negatively correlated with optimal growth temperature it might explain the deviations we observe. Unfortunately, we have no way of systematically computing Ne for our sample of prokaryotes. Lynch [83] computed Ne.u, where u is the mutation rate, for 11 bacteria, all mesophiles. Assuming similar mutation rates the 3 slowest growing bacteria are in the 4 top positions. The highest Ne is for Prochorococcus marinus, by far the slowest-growing bacteria in the set and thought to be one of the most abundant species on earth [84]. Also of relevance, the recent application of a model for predicting trophic lifestyle to marine metagenomic data has shown that copiotrophs dominate free-living microbial populations [85]. These results suggest that among free-living bacteria slow-growing species tend to outnumber fast-growing ones. On the other hand, highly reduced symbiotic genomes, supposedly with very low Ne, tend to have high minimal generation times, with some exceptions among Mollicutes. These contradictory trends suggest no obvious correlation between growth rates and effective population size. There is also little evidence for a correlation between maximal growth rates and absolute population sizes. This is because population sizes result from average, not maximal, growth rates and are moderated by the rates of cell death. While most free-living slow-growers lack growth-related traits because they do not endure selection for fast growth, it is possible that bacteria with sudden contractions of population sizes will endure a degradation of growth-related traits leading to lower growth rates. The availability of population data for a growing number of genomes will hopefully allow understanding the evolution of growth-related traits in a population genetics framework.
Besides contributing to the understanding of genome evolution at different maximal growth rates, our results open two important avenues of further research. First, we find that a composite index of codon usage bias allows for the accurate prediction of the type of growth expected from a given prokaryote. Surprisingly, this can be done even with very few genes paving the way for the understanding of a key physiological parameter from partial sequence data alone. This will be of use in the incoming surge of metagenomic data that contains sequences of species about which we ignore everything. Aggregation of metagenomic data into phylotypes will also allow analyzing the diversity of communities in terms of minimal generation times. Second, our data will also be useful in the delineation of experiments aiming at increasing or lowering growth rates in synthetic biology. The production of many metabolites of industrial interest is in conflict with the cell capacity to replicate. Our results point some ways in which prokaryotes can be engineered to grow slower, e.g. by decrease in codon usage in ribosomal proteins, deletion of rRNA operons or ubi-tRNAs. If it is of interest to maximize the production rate of biomass, then inverse interventions, conjugated with experimental evolution, may significantly accelerate the pace at which a lineage acquires the capacity to grow faster. It would be naïve to think that just changing rRNA expression will necessarily result in higher growth rates. In fact, slow growing bacteria often show higher than needed ribosome concentrations [86],[87]. To change growth rates one probably needs to use design growth-related traits optimized genomes and then use experimental evolution to select for high growth rates in environments more favorable to growth than the natural one. Our work, by ranking the information provided by the different traits, provides guidelines for the relevance of each trait in such design. Third, the proposed predictor of minimum generation times applied to metagenomic datasets allows testing central theories in microbial ecology associated with growth rates. Metagenomic datasets give a unique access to whole microbial communities, regardless of their cultivability. As metagenomics develops, longer scaffolds will be available, with enough information to predict the growth rate of the corresponding species. Also, key genomes for specific niches are being sequenced, with example of the Human Microbiome Project sequencing 1000 microbial reference genomes. The emergence of all this new material will open new avenues of research in microbial ecology and evolution.
Materials and Methods
Whole genome data
We retrieved 214 genome sequences, 1 per species, from GenBank Genomes (ftp://ftp.ncbi.nih.gov/genomes/Bacteria/). Genes were extracted from annotation data and pseudo-genes were ignored. Genes of the transcription/translation machinery (RNA polymerase, rRNAs, ribosomal proteins) were identified by the annotation fields, or, when not possible, by homology from the genomes of closely related species. A pair of genes were regarded as orthologous if they were reciprocal best hits with more than 40% sequence similarity and less than 20% difference in protein length, as measured by a end-gaps free sequence alignment. tRNAs were searched with tRNAscanSE [88] using the default parameters for bacteria or archaea. When the tRNA anticodon matched a previously published list of nearly ubiquitous tRNAs [35] it was included in the list of ubi-tRNAs. Optimal growth temperatures (OGT) were retrieved for 204 of the 214 organisms from the DSMZ database (http://www.dsmz.de/microorganisms/). Psychrophiles and thermophiles were defined as organisms whose OGT is under 15°C and over 60°C, respectively. We extracted from primary literature the minimal generation times (d) for the 214 species of bacteria and archaea (Table S1).
Metagenomic data
The contigs from the 3 metagenomic datasets used in Figure 7 were retrieved from GenBank (http://www.ncbi.nlm.nih.gov/books/bv.fcgi?rid=metagenomics), including the acid mine drainage biofilm (AADL01000001–AADL01002534), the Waseca County Farm Soil (AAFX01000001–AAFX01139340), and the human distal gut microbiome (AAQK01000001–AAQK01010488, AAQL01000001–AAQL01012020). The contigs from the 13 healthy humans gut microbiomes of the Human Metagenome Consortium Japan (HMGJ; http://www.metagenome.jp/) were also retrieved from GenBank under the following accession numbers: subject F1-S (BAAU01000001–BAAU01028900), subject F1-T (BAAV01000001–BAAV01036326), subject F1-U (BAAW01000001–BAAW01016539), subject F2-V (BAAX01000001–BAAX01036455), subject F2-W (BAAY01000001–BAAY01030198), subject F2-X (BAAZ01000001–BAAZ01031237), subject F2-Y (BABA01000001–BABA01035177), subject In-A (BABB01000001–BABB01020226), subject In-B (BABC01000001–BABC01009958), subject In-D (BABD01000001–BABD01037296), subject In-E (BABE01000001–BABE01020532), subject In-M (BABF01000001–BABF01016164) and subject In-R (BABG01000001–BABG01034797).
Distance to the origin of replication
Predicted origins of replication were retrieved from DoriC database (http://tubic.tju.edu.cn/doric/) [89]. Archaea often have multiple and difficult to assess origins of replication [90]. Therefore, archaea were excluded from the calculation of distances to the origin of replication and subsequent correlations to growth rate.
Relative distance to the origin of replication is calculated as the smallest circular distance of the gene to the origin of replication divided by half of the chromosome size. Hence, 0 corresponds to the origin of replication, 0.5 to half the replicon and 1 to the position opposite to the origin, typically the terminus.
Codon usage bias
We used two different measures to assess the difference in codon usage biases between the average and the highly expressed genes: the ΔENC′ and the S indices.
ΔENC′ is an empirical estimator of the strength of selection acting on codon usage bias in highly expressed genes [35]. For each genome, the ENC′ value [91] was calculated separately for the concatenation of all the coding sequences (ENC′all) and for the concatenation of the ribosomal protein genes (ENC′rib), using the average coding nucleotide frequency. The ΔENC′ was then calculated as:(4)S is also an estimator of the strength of selection acting on codon usage bias, but based on the mutation-selection balance between pairs of codons, where one is fitter. Following Sharp, we compute S using the frequency of codons for four amino acids: Phe (C1 = UUC, C2 = UUU), Ile (C1 = AUC, C2 = AUU), Tyr (C1 = UAC, C2 = UAU), Asn (C1 = AAC, C2 = AAU). Codons C1 and C2 are recognized by the same tRNA. By Watson-Crick rules, the codon-anticodon interaction between C1 and the anticodon is better. Hence, C1 should be favored in genes having translation-associated codon usage bias. For each of the 4 amino acids mentioned above, we calculated the frequency of the optimal codon P = C1/(C1+C2) in all proteins (Pall) and in ribosomal proteins (Prib). The S component for each amino acid is then given by:(5)S is the weighted mean of the Si values [46].
As alternatives to ΔENC′ and S, we also tested the use of the genome ENC′ and of ribosomal proteins ENC′. The former was a very bad predictor of growth rates (R2 = 0.12), the latter was as good predictor as ΔENC′ (respectively R2 = 0.53 and R2 = 0.54, for the mesophiles), but correlated with the genome G+C content, suggesting that while the genome ENC′ has little informative power it calibrates for compositional biases when it's included in the computation of ΔENC′.
Codon usage bias adapted to metagenomic data
Both ΔENC′ and S calculations were adapted to use gene-level information (ΔENC′a and Sa) instead of the genomic-level information (concatenation of the genes as previously done). When analyzing metagenomes, concatenating all of the sequences would erroneously increase the mean effective number of codons (ENC′) of the dataset, because each organism might have a different codon usage bias (i.e. a different set of preferred codons). This is not the case for the calculation of S [46], which only takes into account the codon usage for 4 amino acids, for which the optimal codon is the same in all species. The problem of analyzing a mixture a sequences from different species can be circumvented if ENC′ is calculated gene by gene.
Thus, we calculated for each gene separately, ENC′ and P (P = C1/C1+C2, for the 4 amino acids indistinctly) (C1 and C2 codons are listed above in the ‘Codon usage bias’ section). Then, we calculate the average ENC′ and P for the set of genes coding for ribosomal proteins and for the all the genes separately ( and , and ). Afterwards, we compute ΔENC′a and Sa using:(6)(7)AWK and R scripts and C source of the programs to compute ENC′ and P calculations for each gene are available from the authors.
For the set of all genes, open reading frames (ORFs) with a minimum size of 450bp were retrieved using EMBOSS function getorf. For the set of highly expressed genes, ribosomal proteins were retrieved by similarity with a database of ribosomal proteins of all sequenced genomes available to date (e-value<10−5).
Bootstrap on metagenomes
The error bars of average growth rates of environmental metagenomes correspond to the standard deviation of the predictions generated with 1000 bootstraps on the metagenome dataset of all genes and highly expressed genes independently and simultaneously. In order to compare the average predicted minimal doubling time of different metagenomes, we computed the difference between the predictions of pairs of environments, for each bootstrap iteration. The significance (p-value) of the comparison of averages of different metagenomes was calculated as the proportion of the differences that didn't match the expectation. For example, for the acid mine (AM) and the farm soil (FS), we calculated for each iteration dAM-dFS. The acid mine's average doubling time is larger than the farm soil. The significance of this difference has a p-value p‰ if one finds p out of 1000 iterations where dAM-dFS<0 (e.g. 10 iterations<0 give a p-value = 0.01). If no such iteration is found we mark p<0.001.
Discrete classification
The observed minimum generation times (d) of the mesophilic species were discretized into four classes: very fast (d<1h, N = 46), fast (1h<d<2h, N = 26), intermediate (2h<d<5h, N = 41) and slow (d≥5h, N = 74). The predicted continuous values for the 187 species were obtained with the mesophilic predictor, using 5 highly expressed genes and 5 other genes (both randomly chosen in the complete sets, 1000 random experiments). These were discretized in the same way and compared to the observed ones. The accuracy of the classification was evaluated from the proportion of exact, approximate and wrong classifications (%), respectively defined as the proportion of 1) predictions matching the same observed class, 2) predictions matching the same observed class or the adjacent ones (e.g. predicted ‘fast’ when actually ‘very fast’) and 3) slow growers predicted as fast or very fast and inversely.
Box-Cox transformations
The Box-Cox power transformation aims at ensuring that the usual assumptions for linear models hold [55]. We used it to linearize the relation between minimum generation time (d) and the other variables. For example, in the association between d and F, a Box-Cox transformation was applied to d:(8)
Principal component analysis
In order to retrieve the most relevant information of ΔENC′ and S combined, a PCA was performed and the first principal component, which was highly correlated to growth rate, was named F.(9)
Derivation of the predictor
By linear regression, the following relation between the transformation of minimum generation time (eq. 8) and the first principal component (F) of codon usage bias indices ΔENC′ and S (eq. 9):Replacing F (eq. 9), we obtain:Reversing the transformation of minimum generation time (eq. 8), we obtain our predictor (eq. 3):
Phylogenetic analysis
We build a phylogenetic tree using the 16S rDNA subunit for each species. We made a multiple alignment of the 16S sequences with MUSCLE [92], followed by manual correction with SEAVIEW [93]. The tree was computed by maximum likelihood with PHYML [94] using the model HKY+Γ(4)+I. Pairwise phylogenetic distances were computed from the distance matrix. Phylogenetic contrast analysis was done with the ape package in R using generalized estimation equations (GEE) [95].
Pairwise relative differences
Pairwise differences of minimum doubling time Δd were calculated for the 214 prokaryotes. The difference of the box-cox transforms of doubling times for the pair of species were normalized by the maximum observed difference in the 22791 pairs.(10)The relative pairwise differences in codon usage bias indices ΔENC′, S, F and G+C content were calculated the same way, for the 188 prokaryotes with known origins of replication.
Classification of metagenomes into pseudo-genomes
We mapped each protein of a given metagenome dataset in a given template genome. Template genomes were taken among 601 completely sequenced genomes. For each species we chose one single strain to avoid statistical bias. By default we used the first published strain. Mapping was done as follows: 1) for each protein of the metagenome dataset we find highly similar homologues within every proteome using quickhit, a companion of swelfe [96], that allows to quickly find highly similar protein sequences. 2) The hits were then aligned using exact end-gap free Needleman-Wunsch alignments. 3) A given protein was added to one, and only one, pseudo-genome if it matched the corresponding template genome, if this was the best among all matches and if the protein similarity was higher than 95%.
Supporting Information
Zdroje
1. KlappenbachJA
DunbarJM
SchmidtTM
2000 rRNA operon copy number reflects ecological strategies of bacteria. Appl Environ Microbiol 66 1328 1333
2. DethlefsenL
SchmidtTM
2007 Performance of the translational apparatus varies with the ecological strategies of bacteria. J Bacteriol 189 3237 3245
3. StevensonBS
SchmidtTM
2004 Life history implications of rRNA gene copy number in Escherichia coli. Appl Environ Microbiol 70 6670 6677
4. GottschalJC
1985 Some reflections on microbial competitiveness among heterotrophic bacteria. Antonie Van Leeuwenhoek 51 473 494
5. MonodJ
1949 The growth of bacterial cultures. Annu Rev Microbiol 3 371 394
6. NeidhardtFC
1999 Bacterial growth: constant obsession with dN/dt. J Bacteriol 181 7405 7408
7. PanikovNS
1995 Microbial Growth Kinetics London Chapman & Hall
8. FreilichS
KreimerA
BorensteinE
YosefN
SharanR
2009 Metabolic-network-driven analysis of bacterial ecological strategies. Genome Biol 10 R61
9. MerhejV
Royer-CarenziM
PontarottiP
RaoultD
2009 Massive comparative genomic analysis reveals convergent evolution of specialized bacteria. Biol Direct 4 13
10. ReadAF
1994 The evolution of virulence. Trends Microbiol 2 73 76
11. vanBaalenM
SabelisMW
1995 The dynamics of multiple infection and the evolution of virulence. American Naturalist 146 881 910
12. SouliM
GalaniI
GiamarellouH
2008 Emergence of extensively drug-resistant and pandrug-resistant Gram-negative bacilli in Europe. Euro Surveill 13
13. LewisK
2007 Persister cells, dormancy and infectious disease. Nat Rev Microbiol 5 48 56
14. SchutF
PrinsR
GottschalJ
1997 Oligotrophy and pelagic marine bacteria: facts and fiction. Aquatic Microbial Ecology 12 177 202
15. KochAL
2001 Oligotrophs versus copiotrophs. Bioessays 23 657 661
16. KochAL
1971 The adaptive responses of Escherichia coli to a feast and famine existence. Adv Microb Physiol 6 147 217
17. ButtonDK
1991 Biochemical basis for whole-cell uptake kinetics - specific affinity, oligotrophic capacity, and the meaning of the Michaelis constant. Appl Environ Microbiol 57 2033 2038
18. BremerH
DennisPP
1996 Modulation of chemical composition and other parameters of the cell by growth rate. Escherichia coli and Salmonella: cellular and molecular biology Washington DC ASM Press 1553 1569
19. CondonC
LiverisD
SquiresC
SchwartzI
SquiresCL
1995 rRNA operon multiplicity in Escherichia coli and the physiological implications of rrn inactivation. J Bacteriol 177 4152 4156
20. StevensonBS
SchmidtTM
1998 Growth rate-dependent accumulation of RNA from plasmid-borne rRNA operons in Escherichia coli. J Bacteriol 180 1970 1972
21. KubitschekHE
NewmanCN
1978 Chromosome replication during the division cycle in slowly growing, steady-state cultures of three Escherichia coli B/r strains. J Bacteriol 136 179 190
22. SchmidMB
RothJR
1987 Gene location affects expression level in Salmonella typhimurium. J Bacteriol 169 2872 2875
23. SousaC
de LorenzoV
CebollaA
1997 Modulation of gene expression through chromosomal positioning in Escherichia coli. Microbiology 143 2071 2078
24. DryseliusR
IzutsuK
HondaT
IidaT
2008 Differential replication dynamics for large and small Vibrio chromosomes affect gene dosage, expression and location. BMC Genomics 9 559
25. CouturierE
RochaEPC
2006 Replication-associated gene dosage effects shape the genomes of fast-growing bacteria but only for transcription and translation genes. Mol Microbiol 59 1506 1518
26. DongH
NilssonL
KurlandCG
1996 Co-variation of tRNA abundance and codon usage in Escherichia coli at different growth rates. J Mol Biol 260 649 663
27. IkemuraT
1985 Codon usage and tRNA content in unicellular and multicellular organisms. Mol Biol Evol 2 13 34
28. GranthamR
GautierC
GouyM
JacobzoneM
MercierR
1981 Codon catalog usage is a genome strategy modulated for gene expressivity. Nucleic Acids Res 9 r43 74
29. KarlinS
MrazekJ
2000 Predicted highly expressed genes of diverse prokaryotic genomes. J Bacteriol 182 5238 5250
30. BulmerM
1991 The selection-mutation-drift theory of synonymous codon usage. Genetics 129 897 907
31. KarlinS
BarnettMJ
CampbellA
FisherRF
MrazekJ
2003 Predicting gene expression levels from codon usage biases in a-proteobacterial genomes. Proc Natl Acad Sci U S A 100 7313 7318
32. SharpPM
LiWH
1987 The Codon Adaptation Index - a Measure of Directional Synonymous Codon Usage Bias, and Its Potential Applications. Nucleic Acids Research 15 1281 1295
33. AiyarSE
GaalT
GourseRL
2002 rRNA promoter activity in the fast-growing bacterium Vibrio natriegens. J Bacteriol 184 1349 1358
34. ShresthaPM
NollM
LiesackW
2007 Phylogenetic identity, growth-response time and rRNA operon copy number of soil bacteria indicate different stages of community succession. Environmental Microbiology 9 2464 2474
35. RochaEP
2004 Codon usage bias from tRNA's point of view: redundancy, specialization, and efficient decoding for translation optimization. Genome Res 14 2279 2286
36. HiggsPG
RanW
2008 Coevolution of codon usage and tRNA genes leads to alternative stable states of biased codon usage. Mol Biol Evol 25 2279 2291
37. ArdellDH
KirsebomLA
2005 The Genomic Pattern of tDNA Operon Expression in E. coli. PLoS Comput Biol 1 e12 doi:10.1371/journal.pcbi.0010012
38. SubramanianS
2008 Nearly neutrality and the evolution of codon usage bias in eukaryotic genomes. Genetics 178 2429 2432
39. TadmorAD
TlustyT
2008 A coarse-grained biophysical model of E. coli and its application to perturbation of the rRNA operon copy number. PLoS Comput Biol 4 e1000038 doi:10.1371/journal.pcbi.1000038
40. TouchonM
RochaEP
2007 Causes of insertion sequences abundance in prokaryotic genomes. Mol Biol Evol 24 969 981
41. MiraA
OchmanH
MoranNA
2001 Deletional bias and the evolution of bacterial genomes. Trends Genet 17 589 596
42. HughesD
2000 Co-evolution of the tuf genes links gene conversion with the generation of chromosomal inversions. J Mol Biol 297 355 364
43. LeeZM
BussemaC3rd
SchmidtTM
2009 rrnDB: documenting the number of rRNA and tRNA genes in bacteria and archaea. Nucleic Acids Res 37 D489 493
44. WeiderLJ
ElserJJ
CreaseTJ
MateosM
CotnerJB
2005 The functional significance of ribosomal (r)DNA variation: Impacts on the evolutionary ecology of organisms. Annu Rev Ecol Evol Syst 36 219 242
45. VasiF
TravisanoM
LenskiRE
1994 Long-term experimental evolution in Escherichia coli. II. Changes in life history traits during adaptation to a seasonal environment. Am Nat 144 432 456
46. SharpPM
BailesE
GrocockRJ
PedenJF
SockettRE
2005 Variation in the strength of selected codon usage bias among bacteria. Nucleic Acids Res 33 1141 1153
47. BentleySD
ParkhillJ
2004 Comparative genomic structure of prokaryotes. Annu Rev Genet 38 771 791
48. MustoH
NayaH
ZavalaA
RomeroH
Alvarez-ValinF
2006 Genomic GC level, optimal growth temperature, and genome size in prokaryotes. Biochem Biophys Res Commun 347 1 3
49. GustafssonC
GovindarajanS
MinshullJ
2004 Codon bias and heterologous protein expression. Trends Biotechnol 22 346 353
50. FelsensteinJ
1985 Phylogenies and the comparative method. Am Nat 125 1 15
51. HillCW
GrayJA
1988 Effects of chromosomal inversion on cell fitness in Escherichia coli K - 12. Genetics 119 771 778
52. MuellerS
PapamichailD
ColemanJR
SkienaS
WimmerE
2006 Reduction of the rate of poliovirus protein synthesis through large-scale codon deoptimization causes attenuation of viral virulence by lowering specific infectivity. J Virol 80 9687 9696
53. CelloJ
PaulAV
WimmerE
2002 Chemical synthesis of poliovirus cDNA: generation of infectious virus in the absence of natural template. Science 297 1016 1018
54. GibsonDG
BendersGA
Andrews-PfannkochC
DenisovaEA
Baden-TillsonH
2008 Complete chemical synthesis, assembly, and cloning of a Mycoplasma genitalium genome. Science 319 1215 1220
55. DraperNR
SmithH
1998 Applied regression analysis New York John Wiley & Sons 706
56. GeorletteD
BlaiseV
CollinsT
D'AmicoS
GratiaE
2004 Some like it cold: biocatalysis at low temperatures. FEMS Microbiol Rev 28 25 42
57. MedigueC
KrinE
PascalG
BarbeV
BernselA
2005 Coping with cold: the genome of the versatile marine Antarctica bacterium Pseudoalteromonas haloplanktis TAC125. Genome Res 15 1325 1335
58. ColeST
EiglmeierK
ParkhillJ
JamesKD
ThomsonNR
2001 Massive gene decay in the leprosy bacillus. Nature 409 1007 1011
59. TohH
WeissBL
PerkinSA
YamashitaA
OshimaK
2006 Massive genome erosion and functional adaptations provide insights into the symbiotic lifestyle of Sodalis glossinidius in the tsetse host. Genome Res 16 149 156
60. Gomez-ValeroL
RochaEP
LatorreA
SilvaFJ
2007 Reconstructing the ancestor of Mycobacterium leprae: the dynamics of gene loss and genome reduction. Genome Res 17 1178 1185
61. MoranNA
MiraA
2001 The process of genome shrinkage in the obligate symbiont Buchnera aphidicola. Genome Biol 2 1 12
62. RogallT
WoltersJ
FlohrT
BottgerEC
1990 Towards a phylogeny and definition of species at the molecular level within the genus Mycobacterium. Int J Syst Bacteriol 40 323 330
63. BejaO
SuzukiMT
KooninEV
AravindL
HaddA
2000 Construction and analysis of bacterial artificial chromosome libraries from a marine microbial assemblage. Environ Microbiol 2 516 529
64. TettelinH
RileyD
CattutoC
MediniD
2008 Comparative genomics: the bacterial pan-genome. Curr Opin Microbiol 11 472 477
65. GillSR
PopM
DeboyRT
EckburgPB
TurnbaughPJ
2006 Metagenomic analysis of the human distal gut microbiome. Science 312 1355 1359
66. TringeSG
von MeringC
KobayashiA
SalamovAA
ChenK
2005 Comparative metagenomics of microbial communities. Science 308 554 557
67. TysonGW
ChapmanJ
HugenholtzP
AllenEE
RamRJ
2004 Community structure and metabolism through reconstruction of microbial genomes from the environment. Nature 428 37 43
68. VelicerGJ
LenskiRE
1999 Evolutionary trade-offs under conditions of resource abundance and scarcity: Experiments with bacteria. Ecology 80 1168 1179
69. BakerBJ
BanfieldJF
2003 Microbial communities in acid mine drainage. FEMS Microbiology Ecology 44
70. TorsvikV
OvreasL
ThingstadTF
2002 Prokaryotic diversity–magnitude, dynamics, and controlling factors. Science 296 1064 1066
71. DopsonM
Baker-AustinC
HindA
BowmanJP
BondPL
2004 Characterization of Ferroplasma isolates and Ferroplasma acidarmanus sp. nov., extreme acidophiles from acid mine drainage and industrial bioleaching environments. Appl Environ Microbiol 70 2079 2088
72. CoramNJ
RawlingsDE
2002 Molecular relationship between two groups of the genus Leptospirillum and the finding that Leptospirillum ferriphilum sp. nov. dominates South African commercial biooxidation tanks that operate at 40 degrees C. Appl Environ Microbiol 68 838 845
73. MackieRI
SghirA
GaskinsHR
1999 Developmental microbial ecology of the neonatal gastrointestinal tract. Am J Clin Nutr 69 1035S 1045S
74. LevequeC
2003 Dynamics of communities and ecosystems. Ecology From Ecosystem to Biosphere Enfield, NH Science Publishers Inc 216 221
75. KurokawaK
ItohT
KuwaharaT
OshimaK
TohH
2007 Comparative metagenomics revealed commonly enriched gene sets in human gut microbiomes. DNA Res 14 169 181
76. EckburgPB
BikEM
BernsteinCN
PurdomE
DethlefsenL
2005 Diversity of the human intestinal microbial flora. Science 308 1635 1638
77. LeyRE
BackhedF
TurnbaughP
LozuponeCA
KnightRD
2005 Obesity alters gut microbial ecology. Proc Natl Acad Sci U S A 102 11070 11075
78. IbarraRU
EdwardsJS
PalssonBO
2002 Escherichia coli K-12 undergoes adaptive evolution to achieve in silico predicted optimal growth. Nature 420 186 189
79. MaJ
CampbellA
KarlinS
2002 Correlations between Shine-Dalgarno sequences and gene features such as predicted expression levels and operon structures. J Bacteriol 184 5733 5745
80. RochaEPC
DanchinA
ViariA
1999 Translation in Bacillus subtilis: roles and trends of initiation and termination, insights from a genome analysis. Nucleic Acids Res 27 3567 3576
81. AllenTE
HerrgardMJ
LiuM
QiuY
GlasnerJD
2003 Genome-scale analysis of the uses of the Escherichia coli genome: model-driven analysis of heterogeneous data sets. J Bacteriol 185 6392 6399
82. LithwickG
MargalitH
2003 Hierarchy of sequence-dependent features associated with prokaryotic translation. Genome Res 13 2665 2673
83. LynchM
ConeryJS
2003 The origins of genome complexity. Science 302 1401 1404
84. PartenskyF
HessWR
VaulotD
1999 Prochlorococcus, a marine photosynthetic prokaryote of global significance. Microbiol Mol Biol Rev 63 106 127
85. LauroFM
McDougaldD
ThomasT
WilliamsTJ
EganS
2009 The genomic basis of trophic strategy in marine bacteria. Proc Natl Acad Sci U S A 106 15527 15533
86. PangH
WinklerHH
1994 The concentrations of stable RNA and ribosomes in Rickettsia prowazekii. Mol Microbiol 12 115 120
87. FegatellaF
LimJ
KjellebergS
CavicchioliR
1998 Implications of rRNA operon copy number and ribosome content in the marine oligotrophic ultramicrobacterium Sphingomonas sp. strain RB2256. Appl Environ Microbiol 64 4433 4438
88. LoweT
EddyS
1997 tRNAscan-SE: a program for improved detection of transfer RNA genes in genomic sequence. Nucleic Acids Res 25 955 964
89. GaoF
ZhangCT
2007 DoriC: a database of oriC regions in bacterial genomes. Bioinformatics 23 1866 1867
90. KelmanLM
KelmanZ
2004 Multiple origins of replication in archaea. Trends Microbiol 12 399 401
91. NovembreJA
2002 Accounting for Background Nucleotide Composition When Measuring Codon Usage Bias. Mol Biol Evol 19 1390 1394
92. EdgarRC
2004 MUSCLE: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res 32 1792 1797
93. GaltierN
GouyM
GautierC
1996 SEAVIEW and PHYLO_WIN: two graphic tools for sequence alignment and molecular phylogeny. Comput Appl Biosci 12 543 548
94. GuindonS
GascuelO
2003 A simple, fast, and accurate algorithm to estimate large phylogenies by maximum likelihood. Syst Biol 52 696 704
95. ParadisE
ClaudeJ
2002 Analysis of comparative data using generalized estimating equations. J Theor Biol 218 175 185
96. AbrahamAL
RochaEP
PothierJ
2008 Swelfe: a detector of internal repeats in sequences and structures. Bioinformatics 24 1536 1537
Štítky
Genetika Reprodukční medicína
Článek Activation of Mutant Enzyme Function by Proteasome Inhibitors and Treatments that Induce Hsp70Článek Maternal Ethanol Consumption Alters the Epigenotype and the Phenotype of Offspring in a Mouse ModelČlánek Genetic Dissection of Differential Signaling Threshold Requirements for the Wnt/β-Catenin PathwayČlánek Distinct Type of Transmission Barrier Revealed by Study of Multiple Prion Determinants of Rnq1
Článek vyšel v časopisePLOS Genetics
Nejčtenější tento týden
2010 Číslo 1- Souvislost haplotypu M2 genu pro annexin A5 s opakovanými reprodukčními ztrátami
- IVF a rakovina prsu – zvyšují hormony riziko vzniku rakoviny?
- Akutní intermitentní porfyrie
- Růst a vývoj dětí narozených pomocí IVF
- Vztah užívání alkoholu a mužské fertility
-
Všechny články tohoto čísla
- Irradiation-Induced Genome Fragmentation Triggers Transposition of a Single Resident Insertion Sequence
- A Major Role of the RecFOR Pathway in DNA Double-Strand-Break Repair through ESDSA in
- Kidney Development in the Absence of and Requires
- Modeling of Environmental Effects in Genome-Wide Association Studies Identifies and as Novel Loci Influencing Serum Cholesterol Levels
- Inverse Correlation between Promoter Strength and Excision Activity in Class 1 Integrons
- Activation of Mutant Enzyme Function by Proteasome Inhibitors and Treatments that Induce Hsp70
- Postnatal Survival of Mice with Maternal Duplication of Distal Chromosome 7 Induced by a / Imprinting Control Region Lacking Insulator Function
- The Werner Syndrome Protein Functions Upstream of ATR and ATM in Response to DNA Replication Inhibition and Double-Strand DNA Breaks
- Maternal Ethanol Consumption Alters the Epigenotype and the Phenotype of Offspring in a Mouse Model
- Understanding Gene Sequence Variation in the Context of Transcription Regulation in Yeast
- miR-30 Regulates Mitochondrial Fission through Targeting p53 and the Dynamin-Related Protein-1 Pathway
- Elevated Levels of the Polo Kinase Cdc5 Override the Mec1/ATR Checkpoint in Budding Yeast by Acting at Different Steps of the Signaling Pathway
- Alternative Epigenetic Chromatin States of Polycomb Target Genes
- Co-Orientation of Replication and Transcription Preserves Genome Integrity
- A Comprehensive Map of Insulator Elements for the Genome
- Environmental and Genetic Determinants of Colony Morphology in Yeast
- U87MG Decoded: The Genomic Sequence of a Cytogenetically Aberrant Human Cancer Cell Line
- The MCM-Binding Protein ETG1 Aids Sister Chromatid Cohesion Required for Postreplicative Homologous Recombination Repair
- Genetic Dissection of Differential Signaling Threshold Requirements for the Wnt/β-Catenin Pathway
- Differential Localization and Independent Acquisition of the H3K9me2 and H3K9me3 Chromatin Modifications in the Adult Germ Line
- Genetic Crossovers Are Predicted Accurately by the Computed Human Recombination Map
- Collaborative Action of Brca1 and CtIP in Elimination of Covalent Modifications from Double-Strand Breaks to Facilitate Subsequent Break Repair
- Distinct Type of Transmission Barrier Revealed by Study of Multiple Prion Determinants of Rnq1
- Genome-Wide Association Study Identifies as a Novel Susceptibility Gene for Osteoporosis
- and Regulate Reproductive Habit in Rice
- Nonsense-Mediated Decay Enables Intron Gain in
- Altered Gene Expression and DNA Damage in Peripheral Blood Cells from Friedreich's Ataxia Patients: Cellular Model of Pathology
- The Systemic Imprint of Growth and Its Uses in Ecological (Meta)Genomics
- The Gift of Observation: An Interview with Mary Lyon
- Genotype and Gene Expression Associations with Immune Function in
- The Elongator Complex Regulates Neuronal α-tubulin Acetylation
- Rising from the Ashes: DNA Repair in
- Mis-Spliced Transcripts of Nicotinic Acetylcholine Receptor α6 Are Associated with Field Evolved Spinosad Resistance in (L.)
- BRIT1/MCPH1 Is Essential for Mitotic and Meiotic Recombination DNA Repair and Maintaining Genomic Stability in Mice
- Non-Coding Changes Cause Sex-Specific Wing Size Differences between Closely Related Species of
- Evidence for Pervasive Adaptive Protein Evolution in Wild Mice
- Evolutionary Mirages: Selection on Binding Site Composition Creates the Illusion of Conserved Grammars in Enhancers
- VEZF1 Elements Mediate Protection from DNA Methylation
- PLOS Genetics
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- A Major Role of the RecFOR Pathway in DNA Double-Strand-Break Repair through ESDSA in
- Kidney Development in the Absence of and Requires
- The Werner Syndrome Protein Functions Upstream of ATR and ATM in Response to DNA Replication Inhibition and Double-Strand DNA Breaks
- Alternative Epigenetic Chromatin States of Polycomb Target Genes
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání




