-
Články
- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Runs of Homozygosity Implicate Autozygosity as a Schizophrenia Risk Factor
Autozygosity occurs when two chromosomal segments that are identical from a common ancestor are inherited from each parent. This occurs at high rates in the offspring of mates who are closely related (inbreeding), but also occurs at lower levels among the offspring of distantly related mates. Here, we use runs of homozygosity in genome-wide SNP data to estimate the proportion of the autosome that exists in autozygous tracts in 9,388 cases with schizophrenia and 12,456 controls. We estimate that the odds of schizophrenia increase by ∼17% for every 1% increase in genome-wide autozygosity. This association is not due to one or a few regions, but results from many autozygous segments spread throughout the genome, and is consistent with a role for multiple recessive or partially recessive alleles in the etiology of schizophrenia. Such a bias towards recessivity suggests that alleles that increase the risk of schizophrenia have been selected against over evolutionary time.
Published in the journal: . PLoS Genet 8(4): e32767. doi:10.1371/journal.pgen.1002656
Category: Research Article
doi: https://doi.org/10.1371/journal.pgen.1002656Summary
Autozygosity occurs when two chromosomal segments that are identical from a common ancestor are inherited from each parent. This occurs at high rates in the offspring of mates who are closely related (inbreeding), but also occurs at lower levels among the offspring of distantly related mates. Here, we use runs of homozygosity in genome-wide SNP data to estimate the proportion of the autosome that exists in autozygous tracts in 9,388 cases with schizophrenia and 12,456 controls. We estimate that the odds of schizophrenia increase by ∼17% for every 1% increase in genome-wide autozygosity. This association is not due to one or a few regions, but results from many autozygous segments spread throughout the genome, and is consistent with a role for multiple recessive or partially recessive alleles in the etiology of schizophrenia. Such a bias towards recessivity suggests that alleles that increase the risk of schizophrenia have been selected against over evolutionary time.
Introduction
Schizophrenia is a highly (.70–.80) heritable [1] neurodevelopmental disorder that has a lifetime prevalence of ∼0.4% [2]. As with most complex disorders, the specific genetic variants that account for a majority of the heritability of schizophrenia remain to be discovered. Two primary factors may explain the difficulty in identifying risk variants. First, the results of genome-wide association studies (GWAS) make it clear that a very large number of genes contribute to schizophrenia risk, and the overall population risk attributable to any one risk variant must be small [3]. Second, although common causal variants almost certainly play an important role in the genetic etiology of schizophrenia [4], [5], it is likely that the frequency distribution of schizophrenia risk alleles is biased towards the rare end of the spectrum [5]. Both of these factors are consistent with selection keeping schizophrenia risk alleles with the largest effects rare, such that no single allele can contribute much to population risk.
If schizophrenia risk alleles have been selected against across evolutionary time (have been under “purifying” selection), another prediction is that schizophrenia risk alleles will be biased towards being recessive. This bias, called directional dominance, occurs in traits subject to purifying selection because selection more efficiently purges the additive and dominant alleles with the strongest effects, leaving the remaining pool of segregating alleles more recessive than otherwise expected [6]. Directional dominance has traditionally been inferred from observations of inbreeding depression, the tendency for offspring of close genetic relatives to have higher rates of congenital disorders and lower fitness [7]. Fitness traits such as survival, reproduction, resistance to disease, and predator avoidance tend to show more inbreeding depression than traits under less intense selection [8]. Interestingly, there are numerous reports of inbreeding effects on human complex traits such as heart disease [9], hypertension [10], osteoporosis [11], cancer [12], and IQ [13], [14].
Studies that have investigated inbreeding effects on schizophrenia using pedigree data suggest that close (e.g., cousin-cousin) inbreeding is a risk factor [15], [16], [17], [18], [19], [20], although three studies have failed to find the predicted effect [21], [22], [23]. However, close inbreeding cannot be a major contributor to schizophrenia risk in industrialized countries given its rarity (<1% of marriages) [24] and the modest increase in the odds of schizophrenia among highly inbred offspring (∼2 - to 5-fold) [15], [16], [17], [18], [19]. Nevertheless, inbreeding is a matter of degree; when distant relatives are considered, everyone is inbred to some degree. It is likely that the parents of the vast majority of people alive today share a common ancestor within ∼15 generations [25]. Although such “distant” inbreeding would be prohibitively difficult to detect from pedigrees, it can leave signals in the genome that are detectable using genome-wide single nucleotide polymorphism (SNP) data.
The inbreeding coefficient of an individual, F, is defined as the probability that two randomly chosen alleles at a homologous locus within an individual are identical by descent (IBD, identical because they are inherited from a common ancestor) [26]. Homozygosity arising from the inheritance of two IBD genomic segments is termed autozygosity. Most estimates of F assume that marker data are independent, and provide an aggregate measure of homozygosity at measured variants across the genome [27]. Recently, however, several investigators have used runs of homozygosity (ROHs; long stretches of homozygous SNPs) to infer autozygososity, and have investigated whether the proportion of the genome that exists in such ROHs, Froh, predicts complex traits [28], [29], [30], [31], [32], [33], [34], [35].
Of several alternative estimates of F, including F estimated by treating markers independently and F estimated from pedigree information, Keller, Visscher, and Goddard [25] recently concluded that Froh is optimal for inferring the degree of genome-wide autozygosity and for detecting inbreeding effects. However, given the small variation in genome-wide Froh in unselected samples (e.g., SD ∼.005), large sample sizes (e.g., >12,000) are necessary to detect inbreeding depression for likely effect sizes in samples not selected for recent inbreeding [25]. Studies investigating the effects of Froh on human complex traits with samples sizes <3,000 and that failed to find significant inbreeding effects [28], [33], [34], [35], [36] are likely to have been underpowered. That said, the only study of Froh in schizophrenia [29] found a very large inbreeding effect, but the effect was observed in a small sample (n = 322) and was significant only for ROHs caused by common haplotypes.
The present study uses imputed SNP data from 17 schizophrenia case-control datasets (total N = 21,844) that are part of the Psychiatric GWAS Consortium (PGC) [3], [37] to investigate whether Froh is associated with higher risk of schizophrenia. We also use an ROH mapping approach to investigate whether specific areas of the genome are predictive of case-control status when autozygous. This study represents the largest investigation to date on the potential consequences of autozygosity as estimated using Froh, and may help elucidate the genetic architecture and natural history of schizophrenia.
Results
SNP data from 9,388 schizophrenia cases and 12,456 controls were collected with institutional review board approval from 17 sites in 11 countries (Table 1). Due to the different SNP platforms used across datasets, the number of SNPs remaining after quality control and linkage-disequilibrium pruning procedures (see below) differed substantially between the datasets (column 6 of Table 1). This induced artifactual differences in ROH statistics across datasets and made it impossible to allelically match ROHs across datasets (see Methods). To circumvent these issues, our main analysis concentrated on ROH results from a common set of imputed SNPs, but we also report results from the raw (non-imputed) SNP data. We imputed 1,252,901 autosomal SNPs in each dataset using BEAGLE [38] and HapMap3 as the reference panel [3]. We used extremely stringent imputation QC thresholds that have been shown to achieve accuracy rates similar to those in genotyped SNPs [39], leaving 398,325 high-quality imputed SNPs. We then removed 303,513 SNPs that were in high linkage disequilibrium (LD) with other SNPs. We defined ROHs as being ≥65 consecutive homozygous SNPs in a row (∼2.3 Mb) among the remaining 94,812 imputed SNPs [40]. We followed the same procedure for each dataset using the raw data, but defined ROHs as being ≥110 consecutive homozygous SNPs in a row (∼1.7 to ∼3.2 Mb, depending on the dataset). ROH thresholds were determined empirically (see Methods) so as to maximize the significance of the schizophrenia-Froh relationship, but as shown below, results differed little for alternative thresholds. Froh was defined as the proportion of an individual's genome that exists in ROHs. Descriptive statistics of ROHs and Froh across individual and combined datasets are shown in Table 1, and distribution of ROH lengths and Froh are shown in Figure 1 (Figure S1 shows the non-truncated distribution of Froh).
Fig. 1. Distributions of ROH Lengths (left) and Froh (right) in the total sample. 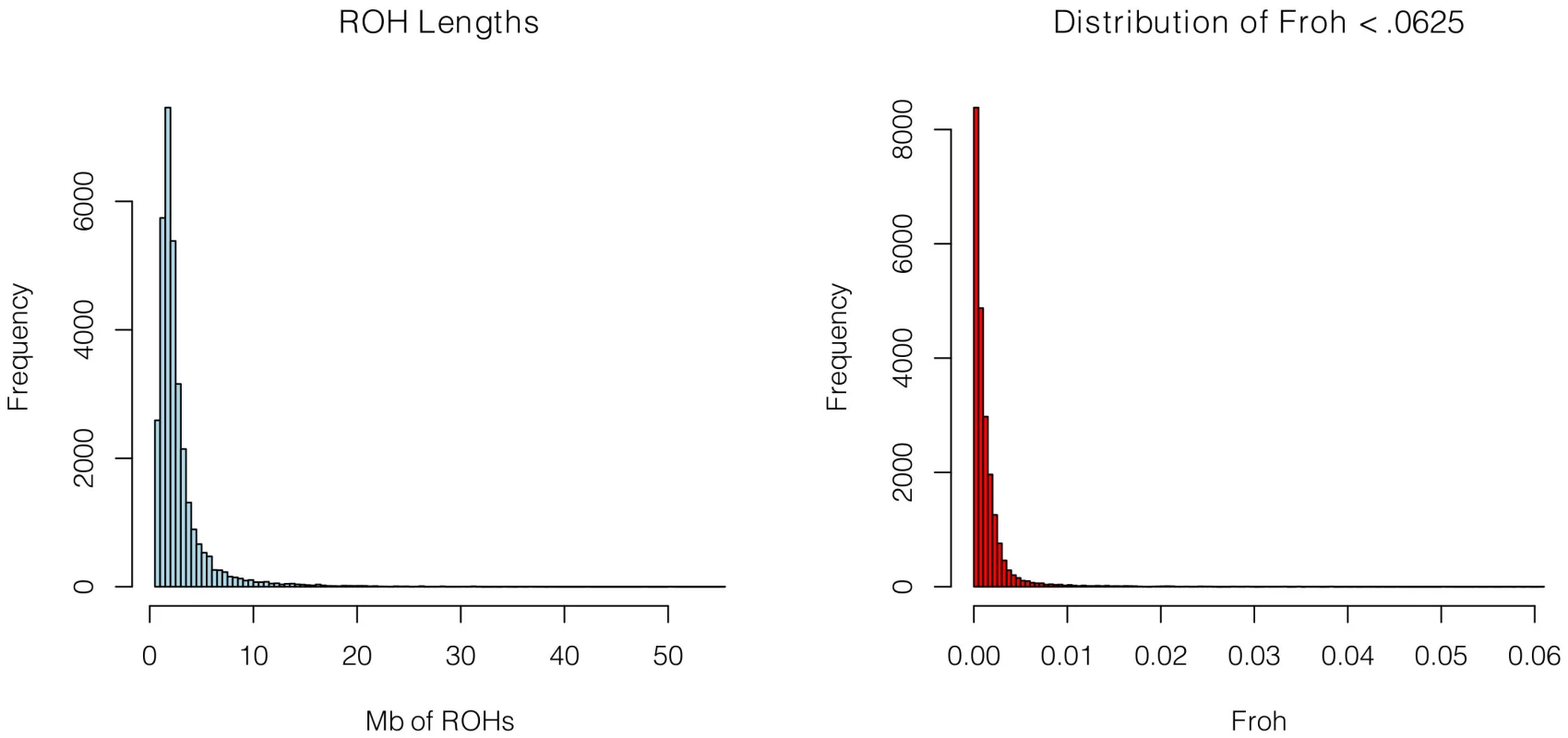
Distributions are based on ROHs from the imputed SNP data. For clarity, the distribution of Froh leaves omits 15 individuals who have Froh>.0625. Tab. 1. Descriptive statistics of SNPs and ROHs (derived from imputed data) across datasets. 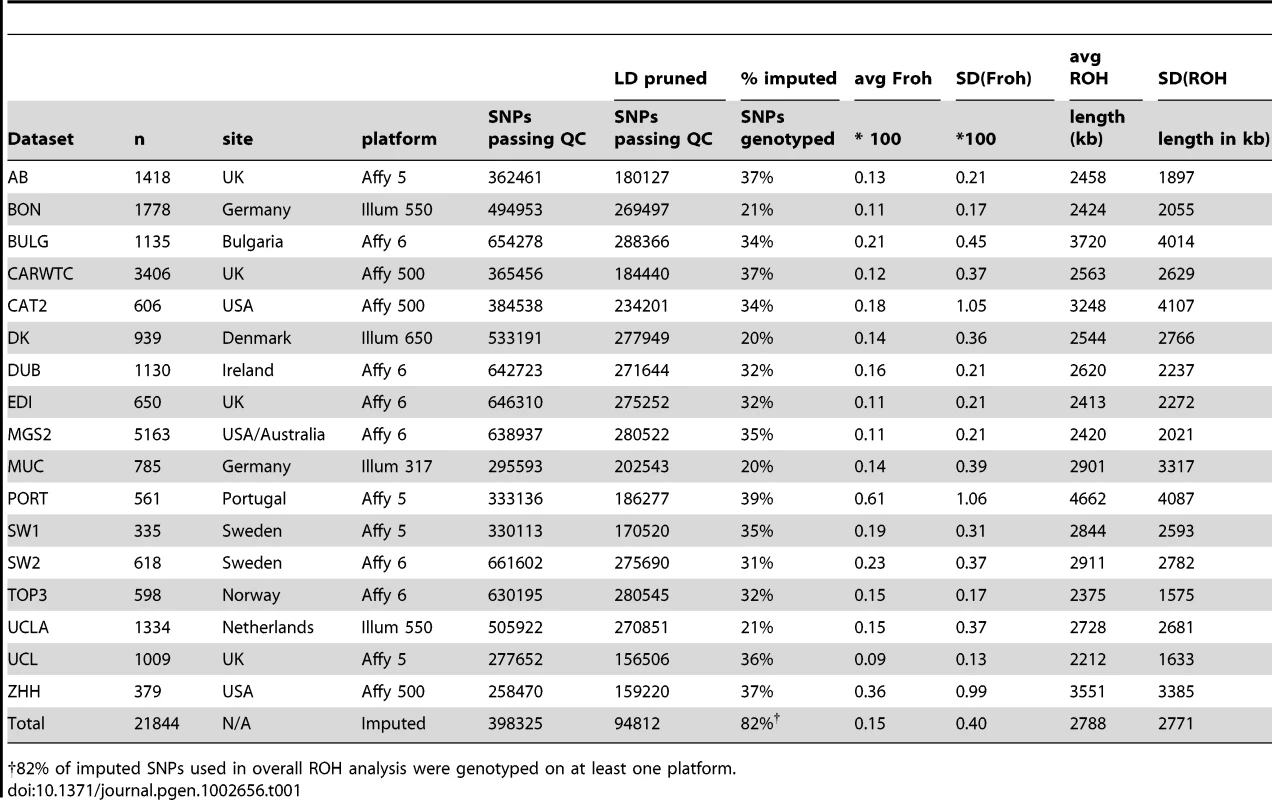
82% of imputed SNPs used in overall ROH analysis were genotyped on at least one platform. ROH burden results
We regressed case-control status on Froh separately in each of the 17 datasets using logistic regression, controlling for potential confounding factors such as population stratification and SNP quality metrics (see Methods). Figure 2 shows the estimated change in odds of schizophrenia for every 1% increase in Froh and the 95% confidence intervals from these 17 logistic regression equations, and Figure S2 shows the same results from an analysis conducted on the raw (non-imputed) SNP data. It should be noted that confidence intervals are symmetric on the log odds scale but asymmetric on the odds ratio scale shown in Figure 2 and Figure S2. As indicated by the confidence intervals, there was a great deal of variability in the estimates of the Froh-schizophrenia association, and none of these 17 odds ratios significantly differed from one. Nevertheless, 13 of the odds ratios were greater than one (i.e., consistent with autozygosity being a schizophrenia risk factor) while 4 were less than one, a result inconsistent with chance (exact binomial test, p = 0.025). More formally, using a mixed linear effects logistic regression model that treated dataset as a random factor (which also controlled for SNP platform because dataset was nested within each platform), the overall association between schizophrenia and Froh in the combined sample was highly significant (β = 16.1, z = 3.44, p = 0.0006 in the imputed data, and β = 17.98, z = 3.89, p = 0.0001 in the raw data). A slope of Froh on schizophrenia of 16.1 is interpreted as saying that for every 0.01 increase in Froh, the odds of schizophrenia are multiplied by , or increased by 17%.
Fig. 2. Estimated changes in odds of schizophrenia for each 1% increase in Froh (odds ratios; asterisks) and their 95% confidence intervals (bars) across the 17 datasets (colored) and for the total sample (black) from the imputed SNP data. 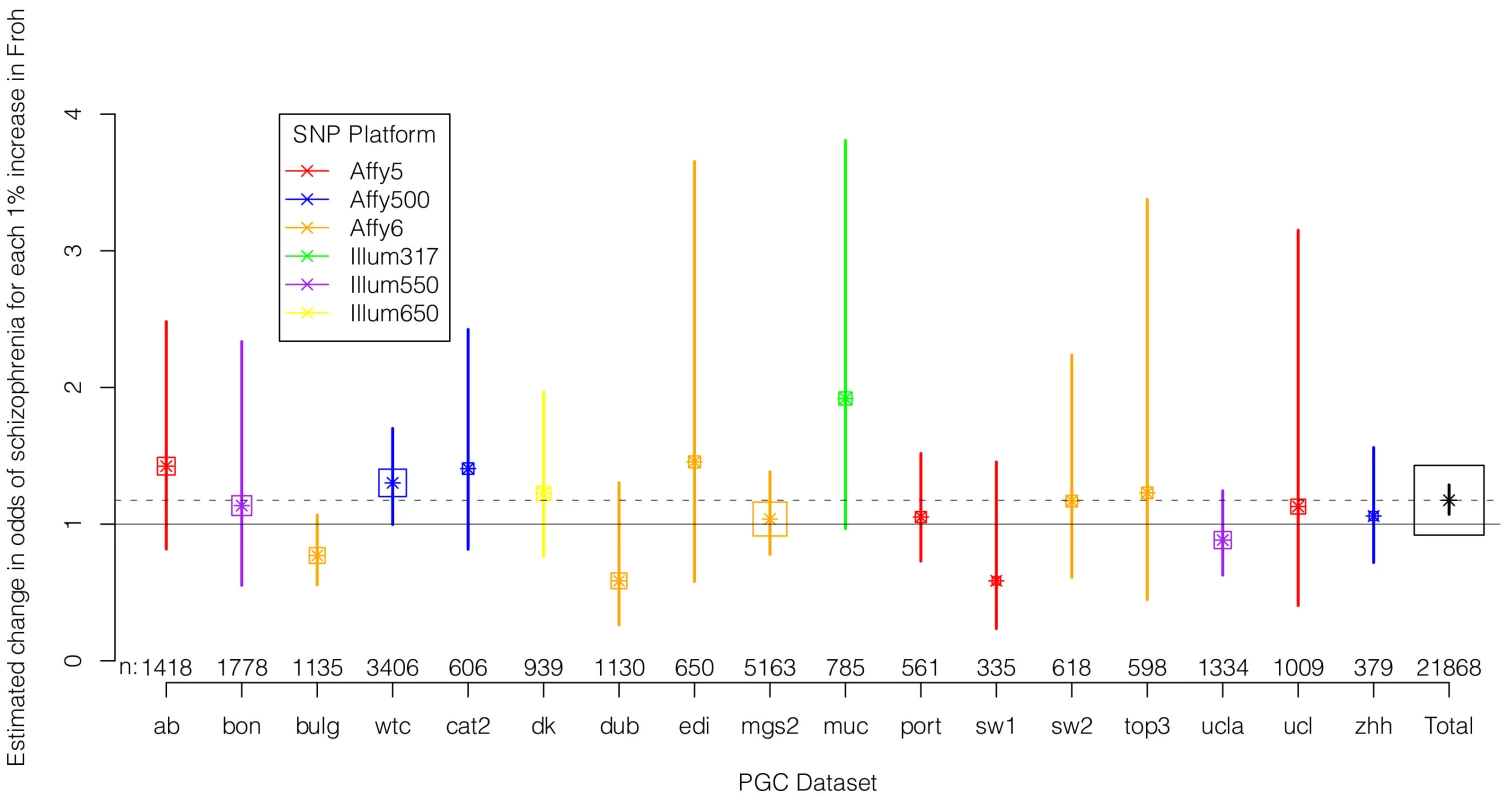
Boxes are proportional to the square root of sample sizes (also shown at the bottom). Dataset names are on the x-axis. Although none of the estimated odds ratios are significantly different from one individually, the overall effect (black) is highly significant. Several secondary analyses were undertaken to explore the robustness and generality of the Froh-schizophrenia association. There was no evidence that the Froh-schizophrenia association differed significantly between datasets ( = 0.253, p = 0.88), and the association remained highly significant in 17 models that removed one dataset at a time. To understand if this association was sensitive to the covariates included in the model, we ran additional models that controlled for no covariates, various combinations of covariates, and dataset-by-covariate interactions. In all of these models, the association between Froh and schizophrenia remained significant. We also found that our conclusions were insensitive to the SNP threshold used to define ROHs; the association between Froh and schizophrenia remained relatively unchanged and significant for all SNP thresholds of ≥40 consecutive SNPs in both the imputed (Figure 3) and raw (Figure S3) data. Finally, both common ROHs (β = 28.5, z = 2.51, p = .012), which arose from haplotypes that were observed often in the data, and uncommon ROHs (β = 20.4, z = 3.29, p = .001) were predictive of case-control status (see Methods).
Fig. 3. Slope estimates (the change in log odds for a 1% increase in Froh; points) and their 95% confidence intervals (bars) of Froh from imputed SNP data predicting schizophrenia for different SNP homozygosity thresholds of calling ROHs. 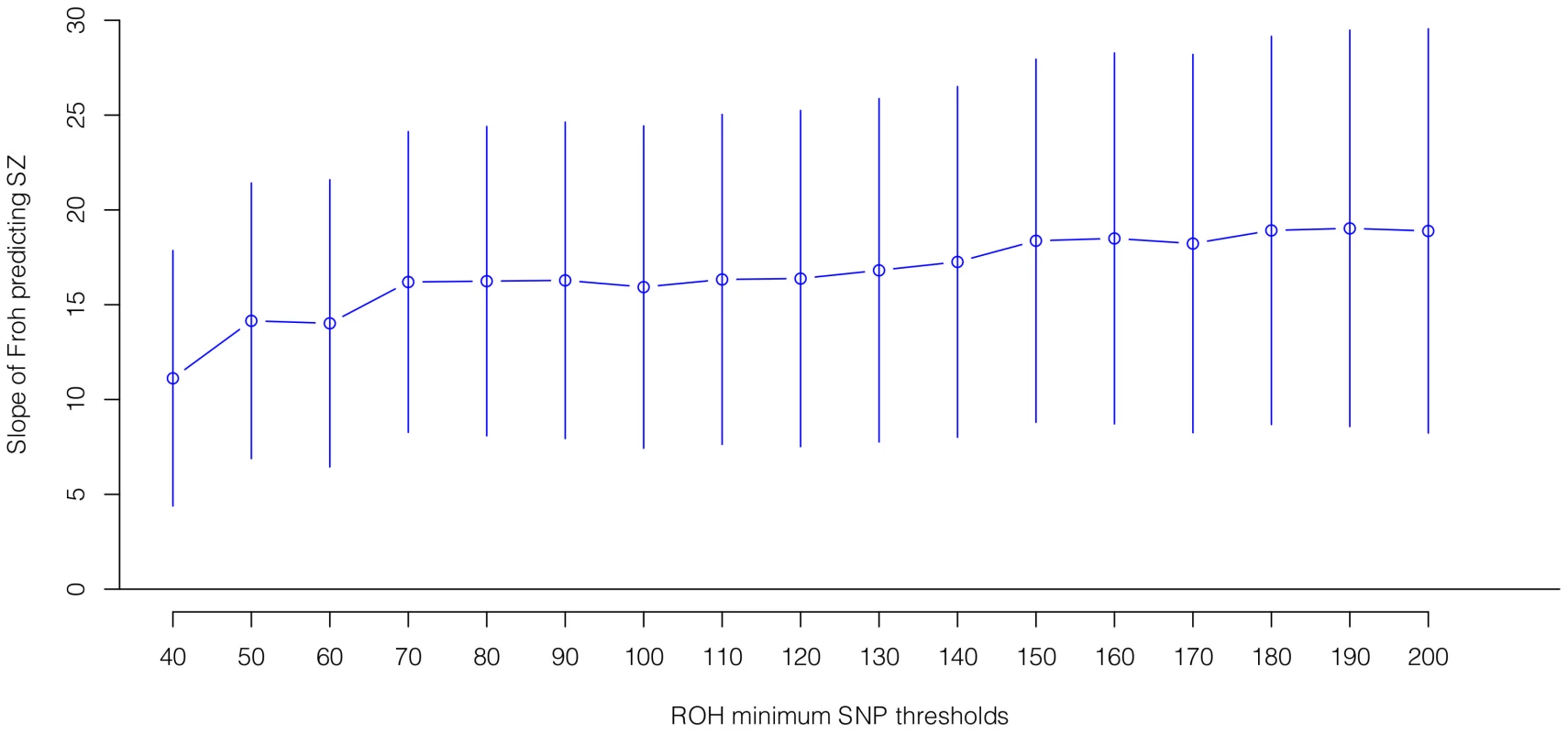
Minimum SNP thresholds for full and reduced models are offset for clarity. All ROH thresholds were significant; the most significant result was for ROHs defined as being 65 or more homozygous SNPs in a row. Autozygosity versus hemizygosity
Copy number variant deletions can create apparent ROHs in SNP data. We could not systematically catalog the overlap between deletions and ROHs in the full dataset because deletion information is not available on the entire sample. However, Levinson and colleagues [41] identified 501,890 deletions (using their “broad” criteria) in the MGS2 dataset (n = 5,163), comprising about one-fourth of the total sample used here. The median length of a deletion in the MGS2 dataset was ∼10 kb, whereas the median length of a ROH was ∼2,000 kb, suggesting that very few deletions would be long enough to qualify as ROHs. Consistent with this expectation, we found that only 10 of 6,480 ROHs in the MGS2 dataset were possible deletions using the algorithm described by McQuillan et al. [31], which called a ROH a “possible deletion” if its total length was <500 kb after removing deletion regions from ROHs. The percentage of ROHs thus classified (0.15%) was similar to the percentage (0.30%) reported by McQuillan et al. [31]. This percentage is too small to have a meaningful impact on our results, because when we removed a larger percentage of ROHs that were identified as being the largest schizophrenia risk factors (see below), the Froh-schizophrenia association remained highly significant. We conclude that ROH results reported above are due to autozygosity rather than hemizygosity.
The effects of close versus distant inbreeding on schizophrenia
A reverse-causation explanation of the Froh-schizophrenia association is possible: people who have a higher “load” of schizophrenia risk alleles (and who transmit this risk to offspring) may be more likely to mate with a relative. This counter-explanation to the causal interpretation of the Froh-schizophrenia relationship is less likely if the relationship holds not only for close inbreeding, but also for autozygosity caused by distant and almost certainly unintended inbreeding (arising from common ancestors who lived many generations ago). One way to investigate this issue is to remove positive outliers on Froh and reassess the Froh-schizophrenia relationship. We reran models after dropping a) two individuals with Froh>0.125, the approximate equivalent of half-sibling inbreeding (β = 15.57, 95% CI(β) = [25.0, 6.14], z = 3.24, p = 0.001); b) 15 individuals with Froh>0.0625, the approximate equivalent of cousin-cousin inbreeding (β = 15.13, 95% CI(β) = [26.1, 4.25], z = 2.73, p = 0.006); c) 56 individuals with Froh>0.03125, the approximate equivalent of half-cousin inbreeding (β = 8.43, 95% CI(β) = [21.43, −4.55], z = 1.27, p = 0.20); d) 942 individuals with Froh>.005, consistent with elevated levels of distant inbreeding (β = 5.17, 95% CI(β) = [34.84, −24.50], z = 0.34, p = .73); and e) 6,101 individuals with Froh scores above the mean level of Froh (β = 66.91, 95% CI(β) = [139.2, −5.4], z = 1.81, p = .07). To test whether the change in significance after dropping outliers was due to the Froh-schizophrenia association being stronger for individuals with high levels of autozygosity, we included a quadratic term (Froh2) in the regression model. In contrast to the highly significant linear term of Froh, the quadratic term of Froh was non-significant (p = .09), suggesting that the effect of autozygosity is linear across the range of Froh observed here.
The simple approach—dropping outliers—to distinguishing the effects of distant versus close inbreeding is problematic for two reasons. First, Froh is naturally extremely right-skewed (Figure 1 and Figure S1), even in large, simulated populations where close inbreeding is disallowed [25], and so dropping even a small number of outliers greatly reduces the variation in Froh, decreases the statistical power to detect an association, and degrades the precision of point estimates. Indeed, there is no evidence that the schizophrenia-Froh association changes as outliers are removed, because the original point estimate (β = 16.1) is contained within every confidence interval above. Thus, the results from dropping outliers demonstrate that the Froh-schizophrenia relationship is not driven by a few highly inbred individuals, but do not allow us to distinguish the effects of distant vs. close inbreeding. Second, individuals with high Froh can arise by chance from the accumulation of many paths of distant inbreeding [25], and are not necessarily the products of close inbreeding. For example, the distribution of lengths of observed ROHs among individuals with Froh>0.0625 is more consistent with inbreeding from common ancestors living ∼6 generations ago than with first cousin inbreeding (Figure 4).
Fig. 4. Distribution of ROH lengths for the 15 individuals with Froh>.0625 in the sample (blue) and the expected lengths of autozygous segments for different levels of inbreeding (red and orange). 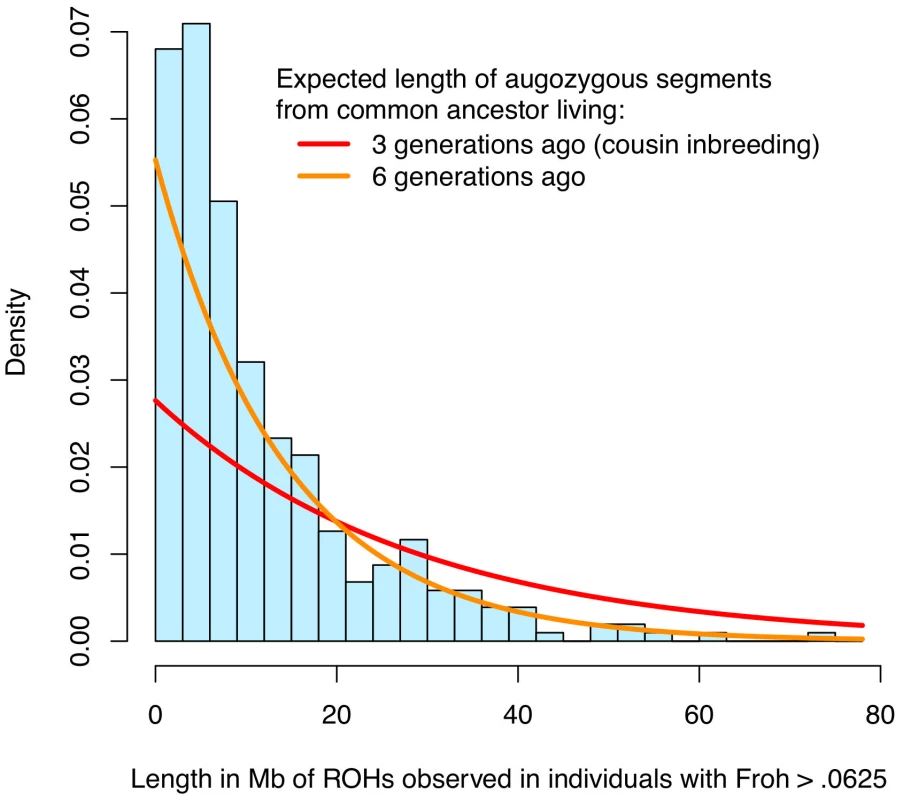
Nearby ROHs that were broken up by a possible heterozygous SNP miscall were joined together. Assuming Haldane's recombination model, the length of an autozygous segment should follow an exponential distribution with mean equal to 1/(2×number of generations since the common ancestor) in Morgans. The figure shows that the distribution of ROH lengths among individuals with Froh>.0625 is most consistent with autozygosity caused by common ancestors between parents who lived ∼6 generations ago. An alternative and more robust approach for assessing the relative importance of distant versus close inbreeding is to compare the effects of short versus long ROHs. We defined Froh<5 Mb as the proportion of the autosome in ROHs of length <5 Mb and Froh>5 Mb as the converse, with 5 Mb chosen as the threshold because the variances of Froh<5 Mb and Froh>5 Mb were equal. An autozygous segment spanning <5 Mb should originate from a common ancestor ≥10 generations ago on average [41]. The effect of Froh<5 Mb (β = 27.6, z = 2.23, p = 0.026) was similar to the effect of Froh>5 Mb (β = 24.3, z = 2.01, p = 0.044), consistent with the hypothesis that autozygosity arising from distant inbreeding is about as much of a schizophrenia risk factor as autozygosity arising from more recent common ancestors.
ROH mapping analysis
The top of Figure 5 shows the −log10 p-values for the 5,742 logistic regressions predicting case-control status from ROHs at each 500 kb bin along the autosome. No regions reached genome-wide significance although two (1p13.2 and 3p24.1) exceeded the “suggestive significance” threshold. Table 2 shows the twelve genes located in these two regions along with their potential functional significances. Neither region has been previously implicated in linkage analyses [42], copy number variant analyses [43], or GWAS meta-analyses [3] of schizophrenia. After recalculating Froh with the two suggestively significant regions removed, results of the burden analysis remained essentially unchanged, showing that these regions have only a minor influence on the overall Froh-schizophrenia association and suggesting that the effect of autozygosity is diffused across the genome.
Fig. 5. Risk and protective effects of ROHs on schizophrenia risk and frequencies of ROHs across the autosome. 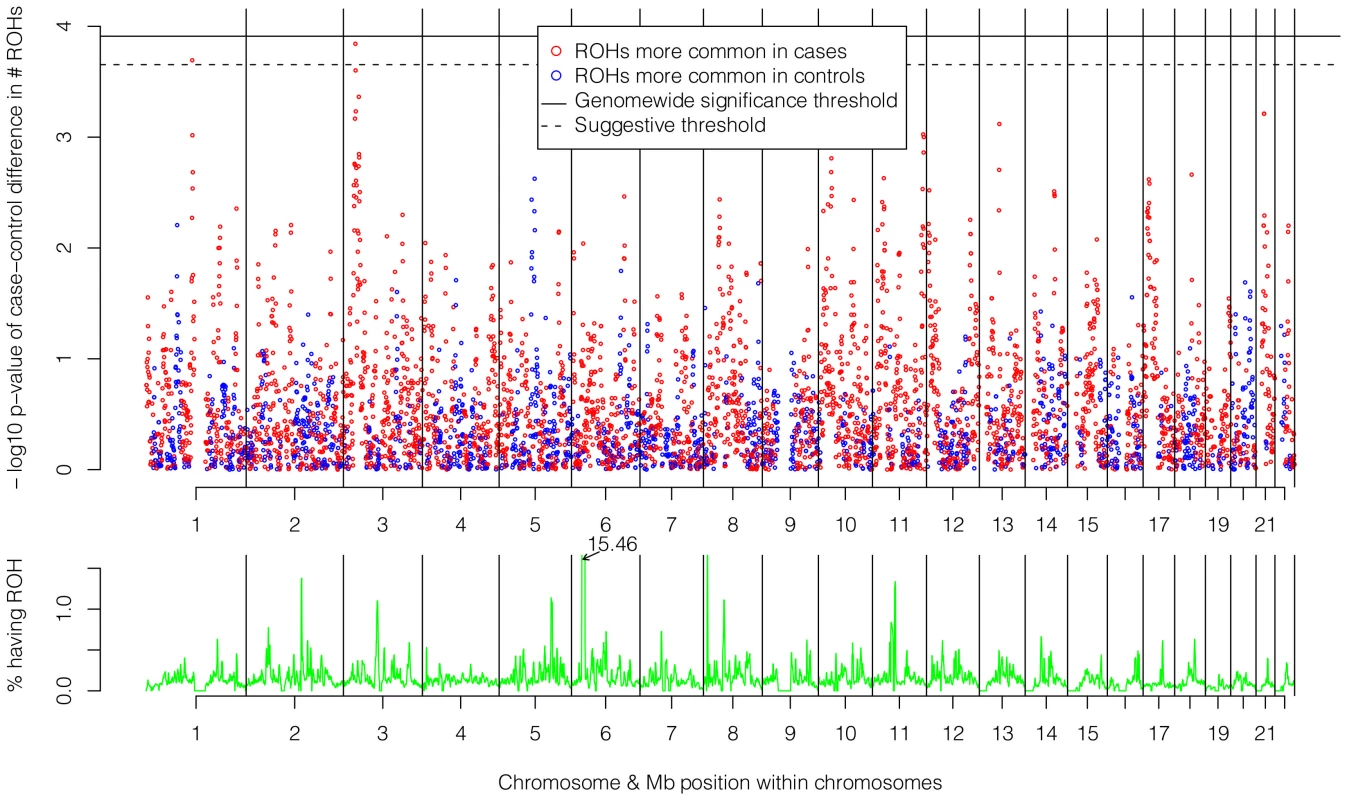
Top panel: −log10 p-values for the risk (red) and protective (blue) effects of ROHs on schizophrenia risk at each 500 kb region along the autosome. Bottom panel: frequencies of ROHs across the autosome. Tab. 2. Genes within the two 500 kb bins that reached “suggestive” significance in the ROH mapping analysis. 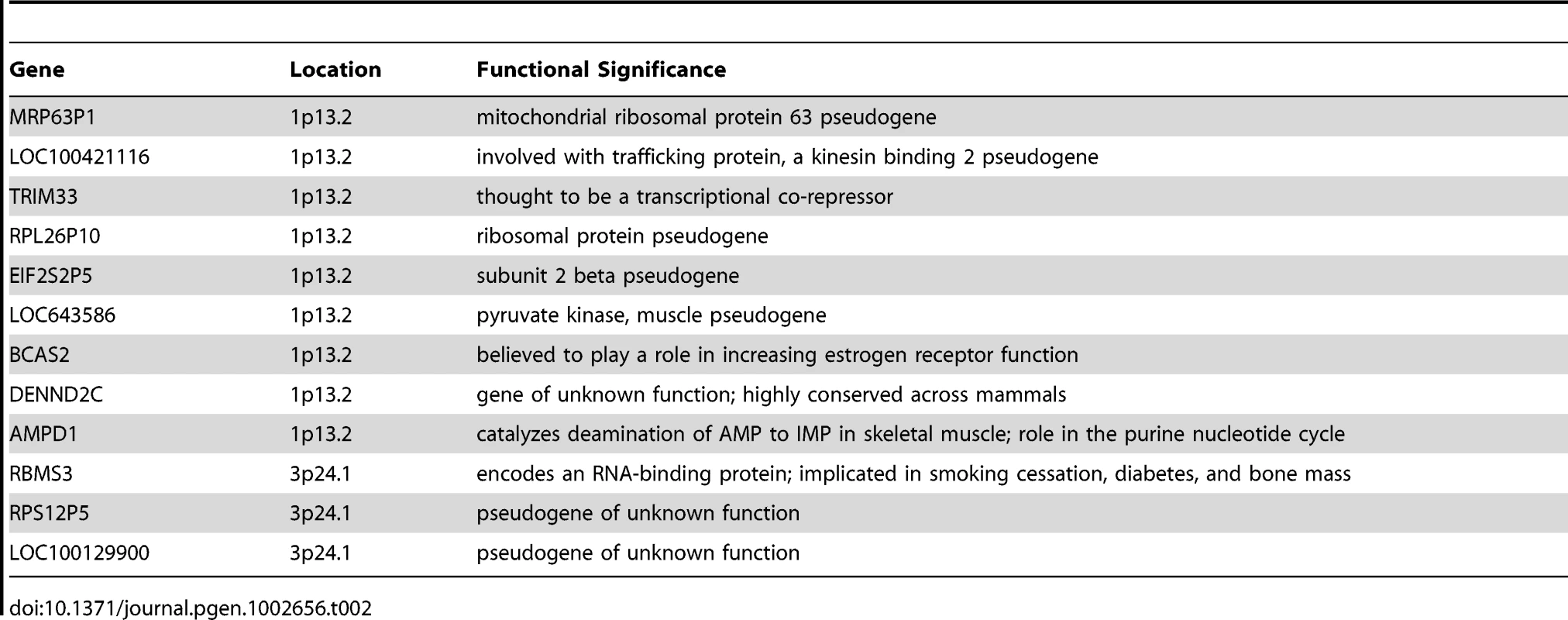
The bottom of Figure 5 shows the frequencies of ROHs occurring at each 500 kb bin across the autosome. With one exception, less than 1.5% of the sample had an ROH at each region. The exception occurs in the Major Histocompatibility Complex region in 6p21.3, where 15.5% of the sample had an ROH. This high number of ROHs is explained by the low recombination and long, common, geographically-specific haplotypes that occur here [44], [45].
Discussion
These results suggest that the odds of schizophrenia increase by ∼17% for every 0.01 increase in the proportion of estimated autosomal autozygosity (Froh). Given the standard deviation of Froh (0.004), this effect is modest, explaining <0.1% of the risk of schizophrenia in outbred populations (Nagelkerke r = 0.026). Nevertheless, this effect implies that close inbreeding is a significant risk factor for schizophrenia. Cousin-cousin inbreeding is predicted to increase the odds of schizophrenia 2.74-fold (by 174%) and second-cousin inbreeding is expected to increase the odds of schizophrenia 1.29-fold (by 29%). These estimates are roughly in line with previous reports on schizophrenia from samples selected based on pedigree inbreeding [15], [16], [17], [18], [19], [20] and similar to the increased risk of major birth defects following close inbreeding [46]. Given that second cousin or closer inbreeding occurs frequently in several world cultures, and that progeny from such unions account for about 10% of the world's population [47], autozygosity may be an important risk factor for schizophrenia worldwide.
The apparent effect of autozygosity on schizophrenia suggests that risk alleles that are more dominant have disappeared over evolutionary time at a faster rate than risk alleles that are more recessive. This is consistent with the hypothesis that alleles that increase the risk of schizophrenia have been under purifying (negative) selection [48].
There are three main limitations to the current study. The most important is that this was a mega-analysis of SNP data collected at 17 different sites using six different platforms. The collection and handling of samples, the distribution of samples on plates, and the calling of SNPs differed between and within sites in ways that were impossible to quantify in the analysis. This certainly added noise to the results, reducing the apparent effect size, but also may have introduced subtle biases. We have tried to statistically control for as many of these as possible, but the possibility remains that uncorrected biases made these results appear stronger or weaker than they actually are.
Second, while our results clearly support the hypothesis that autozygosity is a risk factor for schizophrenia, they are less clear about how confidently we can differentiate the roles of distant versus close inbreeding. On one hand, when enough outliers on Froh values are excluded, the case-control difference is no longer significant. On the other hand, there are good statistical reasons to consider the analysis of short versus long ROHs more valid than the analyses that exclude individuals with the highest Froh values. Thus, the authors favor the conclusion that both distant and close inbreeding are risk factors for schizophrenia. A more definitive answer to this question would either require a substantially larger sample size or a sample of similar size to the current one but drawn from a population with greater variation in levels of distant inbreeding.
A final limitation has to do with the correlational nature of these findings. We argue that the Froh-schizophrenia association is likely to be causal because the association is consistent with a known genetic mechanism, directional dominance, and because the association appears to be as robust for short ROHs as long ROHs. Short ROHs are likely to represent autozygosity caused by distant inbreeding, and therefore seem less likely to differ between parents as a function of their load of schizophrenia risk alleles. Nevertheless, we cannot eliminate the possibility that parents of offspring who have schizophrenia differ in ways that make distant inbreeding more likely, such as an increased propensity to mate with individuals who have culturally, geographically, or ethnically similar backgrounds.
Conclusion
Inbreeding has had a central place in population genetics since its inception, but until recently, the effects of inbreeding could only be investigated from careful analysis of pedigrees and only for close inbreeding. SNP data allows investigation into the effects of potentially very distant inbreeding in non-selected samples, and allows insight into where the signal comes from in the genome. However, unless samples are specifically selected based on inbreeding, very large samples are required to reliably detect effects of autozygosity due to the low variation between individuals in their levels of autozygosity. The present investigation used SNP data from a large sample to conclude that autozygosity is a risk factor for schizophrenia. If the relationship between Froh and schizophrenia is due to directional dominance, such that schizophrenia risk alleles are more recessive than otherwise expected, this suggests that alleles that increase the risk of schizophrenia have been under negative selection ancestrally.
Methods
Psychiatric GWAS consortium data
Full methods are given elsewhere [3]. Briefly, 9,388 schizophrenia cases and 12,456 controls were collected with institutional review board approval from 17 sites in 11 countries (Australia, Bulgaria, Denmark, Germany, Ireland, Netherlands, Norway, Portugal, Sweden, United Kingdom, and Unites States of America; see Table 1). As is typical in the field, individuals with schizophrenia or schizoaffective disorder were included as cases [49] [50]. The quality of phenotypic data was verified by a systematic review of data collection methods to ensure consistency between sites.
Quality control (QC) procedures for raw SNP data
The initial set of samples and SNPs passed common GWAS QC procedures [3]. In particular, we removed a) one individual from any pair of individuals who were related with pi-hat >0.2, b) individuals with non-European ancestry as determined by principal components analysis; c) samples with SNP missingness >0.02; or d) samples with genome-wide heterozygosities >6 standard deviations above the mean. SNPs were excluded if they a) deviated from Hardy-Weinberg equilibrium at p<1×10−6; b) had missingness >0.02; c) showed a minor allele frequency difference to HapMap CEU>0.15; or d) had a missingness difference between cases and controls >0.02. On average the QC processes excluded 15 individuals (0–100) and 38K SNPs (5K–160K) per dataset. The number of SNPs per dataset after QC varied between 250K and 680K (Table 1).
Imputation and QC procedures for imputed SNP data
Six different SNP platforms (Affymetrix 500K, 5.0, and 6.0 chips along with the Illumina 317K, 550K, and 650K chips; Table 1) were used across the 17 datasets. Differences across platforms in SNP densities, frequency distributions, LD patterns, and missingness led to variation in ROH statistics across datasets. For example, the DK dataset contains 280K SNPs after LD pruning (1 SNP per 11 kb) whereas the UCL datset contains 156K SNPs after LD pruning (1 SNP per 21 kb). ROHs therefore would have to be about twice as long in the UCL dataset to qualify, which induces artifactual noise in ROH statistics due to platform effects. This issue is not circumvented by using an ROH threshold based on length rather than number of SNPs; in this case, half as many homozygous SNPs in a row would be required to call an ROH in the less dense dataset. In both cases, the type-I and type-II error rates of autozygosity detection differ systematically between datasets.
To overcome these issues, we imputed dosages for 1,252,901 autosomal SNPs in each dataset using BEAGLE [38] and HapMap3 as the reference panel [3]. We converted imputation dosages to best-guess (highest posterior probability) SNP calls because ROH detection algorithms require discrete SNP calls. Because typical imputation QC thresholds can lead to a high number of missed ROHs, we used extremely stringent imputation QC thresholds that have been shown to achieve accuracy rates similar to those in genotyped SNPs [39]. In particular, we removed 854,566 imputed SNPs with dosage r2<0.90 in any dataset (the dosage r2 is equivalent to MACH's r2 measure described in [51]), that had a dosage r2<0.98 or >1.02 in the overall sample, or that had MAF<0.05, leaving 398,325 high-quality imputed SNPs. Because only ∼100K SNPs are use to make ROH calls (see below), we could afford to lose a large number of imputed SNPs from QC procedures.
ROHs called from imputed data were less variable across platform and across datasets in terms of basic descriptive statistics, in the effects of potential artifacts (e.g., SNP missingness rates and excess heterozygosity on Froh), and in their associations with schizophrenia. We therefore report results on ROHs called from imputed data. However, results for the ROHs called from raw data were similar, and are shown in Figures S2 and S3.
ROH calling procedures
Of three programs investigated (PLINK, GERMLINE, and BEAGLE), a recent investigation by three of the authors of the current report [40] concluded that PLINK (using the –homozyg commands) optimally detected autozygous stretches and maximized power to detect an effect of autozygosity on a phenotype. In particular, the authors recommended: a) pruning for strong LD (removing any SNPs having a multiple R2>0.90 with all other SNPs in a 50 SNP window), which reduced false autozygosity calls by removing redundant markers in SNP-dense regions and by making SNP coverage more uniform; and b) defining ROHs as being ≥65 consecutive homozygous SNPs with no heterozygote calls allowed [40]. We used these recommendations to detect ROHs in all analyses, although to ensure that we did not miss potential effects of autozygosity, we report on results from the specific ROH threshold (number of homozygous SNPs in a row) that minimized the p-value of the Froh-schizophrenia association (see Figure 3 and Figure S3). This threshold was 65 SNPs-in-a-row (spanning ∼2.3 Mb) in the imputed SNP data and 110 SNPs-in-a-row (spanning ∼1.7 Mb to ∼3.2 Mb depending on the dataset) in the raw data. It should be noted that results were relatively insensitive to the specific threshold chosen (Figure 3 and Figure S3). Finally, to ensure that no ROH crossed a region of low SNP density (e.g., a centromere), we also required that ROHs have a density greater than 1 SNP per 200 kb, and we broke an ROH in two if a gap >500 kb existed between adjacent homozygous SNPs.
ROHs can also be categorized by their frequency (how often a particular haplotype creates ROHs at a given location). We used PLINK's –homozyg-group and –homozyg-match arguments to understand whether uncommon ROHs or common ROHs were particularly predictive of case-control status, defining ROHs in a given region as “uncommon” when they allelically matched with 16 (the median) or fewer other ROHs in the combined data; all other ROHs were defined as “common.”
ROH burden analysis
For each individual, we summed the total length of all their ROHs in the autosome and divided by the total SNP-mappable autosomal distance (2.77×109 bases) to derive Froh, the proportion (0 to 1) of the autosome in ROHs. Froh was used as the predictor of case-control status in ROH burden analyses. Froh can be influenced by confounding factors like population stratification (e.g., if background levels of heterozygosity or autozygosity differed by ancestry), low quality DNA leading to incorrect SNP calls, and heterozygosity levels that vary across plates, DNA sources, etc. To control for the effects of stratification, we included the first 20 principal components based on ∼30K SNPs genotyped in all datasets. We also controlled for the percentage of missing calls in the raw SNP data and excess heterozygosity as these track the quality of SNP calls [52]. Using simulations, Keller et al. [25] showed that the ability of Froh to accurately estimate autozygosity is negligibly affected by statistically controlling for excess heterozygosity, and therefore doing so should have minimal effect on results when genotyping error rates are low, but may help elucidate effects of ROHs when such errors are present.
We regressed case-control status on Froh separately in each of the 17 datasets using logistic regression, controlling for the potential confounders discussed above. We then employed a mixed linear effects logistic regression model (using the lme4 package in R version 2.11) to estimate the overall effect of Froh across datasets, treating dataset as a random factor. This also controlled for SNP platform because dataset was nested within each platform (controlling for platform was statistically redundant in a model also controlling for dataset).
ROH mapping analysis
To understand whether any genomic area was predictive of case-control status, we divided the autosome into 5,742 segments of length 500 kb each. At each segment, an individual was scored as either having a ROH that partially or completely overlapped the segment or not. We performed 5,742 logistic regressions, regressing case-control status on whether or not individuals had an ROH in each segment, controlling for covariates described above. To derive a genome-wide significance threshold corrected for multiple testing, we permuted case-control status within the 17 datasets and reran the 5,742 logistic regressions, preserving the most significant result of each permutation. We repeated this permutation 1,000 times. The 50th most significant p-value was the genome-wide significance threshold and the 100th most significant p-value was the “suggestive” genome-wide significance threshold.
Supporting Information
Zdroje
1. SullivanPFKendlerKSNealeMC 2003 Schizophrenia as a complex trait: Evidence from a meta-analysis of twin studies. Arch Gen Psychiat 60 1187 1192
2. SahaSChantDWelhamJMcGrathJ 2005 A systematic review of the prevalence of schizophrenia. PLoS Med 2 e141 doi:10.1371/journal.pmed.0020141
3. Psychiatric GWAS Consortium 2011 Genome-wide association study identifies five novel schizophrenia loci. Nat Gen in press
4. PurcellSMWrayNRStoneJLVisscherPMO'DonovanMC 2009 Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature 460 748 752
5. LeeSHDe CandiaTRipkeSYangJ PGC-SCZ 2012 Estimating the proportion of variation in susceptibility to schizophrenia captured by common SNPs. Nat Genet 44 247 250
6. CharlesworthDWillisJH 2009 The genetics of inbreeding depression. Nat Rev Genet 10 783 796
7. RoffDA 1997 Evolutionary quantitative genetics New York, NY Chapman & Hall
8. DeRoseMARoffDA 1999 A comparison of inbreeding depression in life-history and morphological traits in animals. Evolution 53 1288 1292
9. ShamiSAQaisarRBittlesAH 1991 Consanguinity and adult morbidity in Pakistan. Lancet 338 954
10. RudanISmolej-NarancicNCampbellHCarothersAWrightA 2003 Inbreeding and the genetic complexity of human hypertension. Genetics 163 1011 1021
11. RudanISkaric-JuricTSmolej-NarancicNJanicijevicBRudanD 2004 Inbreeding and susceptibility to osteoporosis in Croatian island isolates. Coll Antropol 28 585 601
12. LebelRRGallagherWB 1989 Wisconsin consanguinity studies. II: Familial adenocarcinomatosis. Am J Med Genet 33 1 6
13. AfzalM 1988 Consquences of consanguinity on cognitive behavior. Beh Genet 18 583 594
14. MortonNE 1979 Effect of inbreeding on IQ and mental retardation. Proc Nat Acad Sci 75 3906 3908
15. AbaskulievAASkobloGV 1975 Inbreeding, endogamy and exogamy among relatives of schizophrenia patients. Genetika 11 145 148
16. BulayevOAPavlovaTABulayevaKB 2009 The effects of inbreeding on aggregation of complex diseases in genetic isolates. Russ J Genet 45 961 968
17. NimgaonkarVLMansourHFathiWKleiLWoodJ 2010 Consanguinity and increased risk for schizophrenia in Egypt. Schizophrenia Res 120 108 112
18. ChalebyK 1987 Cousin Marriages and Schizophrenia in Saudi-Arabia. Brit J Psychiat 150 547 549
19. GindilisVMGainullinRGShmaonovaLM 1989 Genetico-demographic patterns of the prevalence of various forms of endogenous psychoses. Genetika 25 734 743
20. RudanIRudanDCampbellHCarothersAWrightA 2003 Inbreeding and risk of late onset complex disease. J Med Genet 40 925 932
21. AhmedAH 1979 Consanguinity and Schizophrenia in Sudan. Brit J Psychiat 134 635 636
22. ChalebyKTumaTA 1986 Cousin marriages and schizophrenia in Saudi Arabia. Brit J Psychiat 150 547 549
23. SaugstadLØdegardØ 1986 Inbreeding and schizophrenia. Clin Genet 30 261 275
24. BittlesAHNeelJV 1994 The costs of human inbreeding and their implications for variations at the DNA level. Nat Genet 8 117 121
25. KellerMCVisscherPMGoddardME 2011 Quantification of inbreeding due to distant ancestors and its detection using dense SNP data. Genetics 189 237 249
26. WrightS 1922 Coefficients of inbreeding and relationships. Am Nat 56 330 339
27. HanssonBWesterbergL 2002 On the correlation between heterozygosity and fitness in natural populations. Mol Ecol 11 2467 2474
28. VineAEMcQuillinABassNJPereiraAKandaswamyR 2009 No evidence for excess runs of homozygosity in bipolar disorder. Psychiatr Genet 19 165 170
29. LenczTLambertCDeRossePBurdickKEMorganTV 2007 Runs of homozygosity reveal highly penetrant recessive loci in schizophrenia. Proc Natl Acad Sci U S A 104 19942 19947
30. KuCSNaidooNTeoSMPawitanY 2011 Regions of homozygosity and their impact on complex diseases and traits. Hum Genet 129 1 15
31. McQuillanRLeuteneggerALAbdel-RahmanRFranklinCSPericicM 2008 Runs of homozygosity in European populations. Am J Hum Genet 83 359 372
32. KirinMMcQuillanRFranklinCSCampbellHMcKeiguePM 2010 Genomic runs of homozygosity record population history and consanguinity. PLoS ONE 5 e13996 doi:10.1371/journal.pone.0013996
33. SpainSLCazierJBHoulstonRCarvajal-CarmonaLTomlinsonI 2009 Colorectal cancer risk is not associated with increased levels of homozygosity in a population from the United Kingdom. Cancer Res 69 7422 7429
34. Enciso-MoraVHoskingFJHoulstonRS 2010 Risk of breast and prostate cancer is not associated with increased homozygosity in outbred populations. Eur J Hum Genet 18 909 914
35. HoskingFJPapaemmanuilESheridanEKinseySELightfootT 2010 Genome-wide homozygosity signatures and childhood acute lymphoblastic leukemia risk. Blood 115 4472 4477
36. NallsMAGuerreiroRJSimon-SanchezJBrasJTTraynorBJ 2009 Extended tracts of homozygosity identify novel candidate genes associated with late-onset Alzheimer's disease. Neurogenet 10 183 190
37. SullivanPF 2010 The psychiatric GWAS consortium: big science comes to psychiatry. Neuron 68 182 186
38. BrowningBLBrowningSR 2009 A unified approach to genotype imputation and haplotype-phase inference for large data sets of trios and unrelated individuals. Am J Hum Genet 84 210 223
39. HaoKChudinEMcElweeJSchadtEE 2009 Accuracy of genome-wide imputation of untyped markers and impacts on statistical power for association studies. BMC Genet 10 27
40. HowriganDPSimonsonMAKellerMC 2011 Detecting autozygosity through runs of homozygosity: A comparison of three autozygosity detection algorithms. BMC Genom 12 460 475
41. FisherRA 1954 A fuller theory of “junctions” in inbreeding. Heredity 8 187 197
42. NgMYLevinsonDFFaraoneSVSuarezBKDeLisiLE 2009 Meta-analysis of 32 genome-wide linkage studies of schizophrenia. Mol Psychiatry 14 774 785
43. LevinsonDFDuanJOhSWangKSandersAR 2011 Copy number variants in schizophrenia: confirmation of five previous findings and new evidence for 3q29 microdeletions and VIPR2 duplications. Am J Psychiat 168 302 316
44. AlperCALarsenCEDubeyDPAwdehZLFiciDA 2006 The haplotype structure of the human major histocompatibility complex. Hum Immunol 67 73 84
45. TraherneJA 2008 Human MHC architecture and evolution: implications for disease association studies. Int J Immunogenet 35 179 192
46. ChakrabortyRChakravartiA 1977 On consanguineous marriages and the genetic load. Hum Genet 36 47 54
47. BittlesAHBlackML 2010 Evolution in health and medicine Sackler colloquium: Consanguinity, human evolution, and complex diseases. Proc Natl Acad Sci U S A 107 Suppl 1 1779 1786
48. KellerMCMillerGF 2006 Resolving the paradox of common, harmful, heritable mental disorders: Which evolutionary genetic models work best? Behav Brain Sci 29 385 452
49. KendlerKSMcGuireMTGruenbergAMO'HareASpellmanM 1993 The Roscommon family study. Arch Gen Psychiat 50 527 540
50. FaraoneSVBleharMPeppleJMoldinSONortonJ 1996 Diagnostic accuracy and confusability analyses: an application to the Diagnostic Interview for Genetic Studies. Psychol Med 26 401 410
51. MarchiniJHowieB 2010 Genotype imputation for genome-wide association studies. Nat Rev Genet 11 499 511
52. LaurieCCDohenyKFMirelDBPughEWBierutLJ 2010 Quality control and quality assurance in genotypic data for genome-wide association studies. Genet Epidemiol 34 591 602
Štítky
Genetika Reprodukční medicína
Článek A Genome-Wide Screen for Genetic Variants That Modify the Recruitment of REST to Its Target GenesČlánek Population Structure of Hispanics in the United States: The Multi-Ethnic Study of AtherosclerosisČlánek Differing Requirements for RAD51 and DMC1 in Meiotic Pairing of Centromeres and Chromosome Arms inČlánek Transcriptional Regulation of Rod Photoreceptor Homeostasis Revealed by NRL Targetome AnalysisČlánek Cell Contact–Dependent Outer Membrane Exchange in Myxobacteria: Genetic Determinants and MechanismČlánek Formation of Rigid, Non-Flight Forewings (Elytra) of a Beetle Requires Two Major Cuticular Proteins
Článek vyšel v časopisePLOS Genetics
Nejčtenější tento týden
2012 Číslo 4- Akutní intermitentní porfyrie
- Souvislost haplotypu M2 genu pro annexin A5 s opakovanými reprodukčními ztrátami
- Příjem alkoholu a menstruační cyklus
- Doporučení pro diagnostiku a léčbu akutních jaterních porfyrií
- Doc. Miloš Kubánek: Nemocní se srdeční amyloidózou jsou často skryti a sledováni pod jinými diagnózami
-
Všechny články tohoto čísla
- Runs of Homozygosity Implicate Autozygosity as a Schizophrenia Risk Factor
- Modifier Genes and the Plasticity of Genetic Networks in Mice
- The DSIF Subunits Spt4 and Spt5 Have Distinct Roles at Various Phases of Immunoglobulin Class Switch Recombination
- A Genome-Wide Screen for Genetic Variants That Modify the Recruitment of REST to Its Target Genes
- Population Structure of Hispanics in the United States: The Multi-Ethnic Study of Atherosclerosis
- Deep Sequencing of Plant and Animal DNA Contained within Traditional Chinese Medicines Reveals Legality Issues and Health Safety Concerns
- Differing Requirements for RAD51 and DMC1 in Meiotic Pairing of Centromeres and Chromosome Arms in
- Insulin Signaling Mediates Sexual Attractiveness in
- Progressive Telomere Dysfunction Causes Cytokinesis Failure and Leads to the Accumulation of Polyploid Cells
- Long-Range Chromosome Organization in : A Site-Specific System Isolates the Ter Macrodomain
- Regulation of Budding Yeast Mating-Type Switching Donor Preference by the FHA Domain of Fkh1
- Polyglutamine Toxicity Is Controlled by Prion Composition and Gene Dosage in Yeast
- Patterns of Regulatory Variation in Diverse Human Populations
- Sequence-Specific Targeting of Dosage Compensation in Favors an Active Chromatin Context
- Whole-Exome Sequencing and Homozygosity Analysis Implicate Depolarization-Regulated Neuronal Genes in Autism
- Replication Fork Reversal after Replication–Transcription Collision
- Common Variants at 9p21 and 8q22 Are Associated with Increased Susceptibility to Optic Nerve Degeneration in Glaucoma
- Coordinate Regulation of Lipid Metabolism by Novel Nuclear Receptor Partnerships
- Epigenome-Wide Scans Identify Differentially Methylated Regions for Age and Age-Related Phenotypes in a Healthy Ageing Population
- A Coordinated Interdependent Protein Circuitry Stabilizes the Kinetochore Ensemble to Protect CENP-A in the Human Pathogenic Yeast
- Budding Yeast Dma Proteins Control Septin Dynamics and the Spindle Position Checkpoint by Promoting the Recruitment of the Elm1 Kinase to the Bud Neck
- , a Homolog of a Deaf-Blindness Gene, Regulates Circadian Output and Slowpoke Channels
- Transcriptional Regulation of Rod Photoreceptor Homeostasis Revealed by NRL Targetome Analysis
- Cell Contact–Dependent Outer Membrane Exchange in Myxobacteria: Genetic Determinants and Mechanism
- Defective Membrane Remodeling in Neuromuscular Diseases: Insights from Animal Models
- Formation of Rigid, Non-Flight Forewings (Elytra) of a Beetle Requires Two Major Cuticular Proteins
- SPE-44 Implements Sperm Cell Fate
- A Shared Role for RBF1 and dCAP-D3 in the Regulation of Transcription with Consequences for Innate Immunity
- A Companion Cell–Dominant and Developmentally Regulated H3K4 Demethylase Controls Flowering Time in via the Repression of Expression
- The HEN1 Ortholog, HENN-1, Methylates and Stabilizes Select Subclasses of Germline Small RNAs
- Improved Statistics for Genome-Wide Interaction Analysis
- The Probability of a Gene Tree Topology within a Phylogenetic Network with Applications to Hybridization Detection
- Context-Dependent Dual Role of SKI8 Homologs in mRNA Synthesis and Turnover
- Mu Insertions Are Repaired by the Double-Strand Break Repair Pathway of
- Competition between Replicative and Translesion Polymerases during Homologous Recombination Repair in Drosophila
- An Unbiased Assessment of the Role of Imprinted Genes in an Intergenerational Model of Developmental Programming
- Type 2 Diabetes Risk Alleles Demonstrate Extreme Directional Differentiation among Human Populations, Compared to Other Diseases
- Mutations in and Cause “Splashed White” and Other White Spotting Phenotypes in Horses
- Fine-Scale Mapping of Natural Variation in Fly Fecundity Identifies Neuronal Domain of Expression and Function of an Aquaporin
- Dynamics of Brassinosteroid Response Modulated by Negative Regulator LIC in Rice
- Genetic Inhibition of Solute-Linked Carrier 39 Family Transporter 1 Ameliorates Aβ Pathology in a Model of Alzheimer's Disease
- The Functions of Mediator in Support a Role in Shaping Species-Specific Gene Expression
- Patterns of Ancestry, Signatures of Natural Selection, and Genetic Association with Stature in Western African Pygmies
- Dissection of Pol II Trigger Loop Function and Pol II Activity–Dependent Control of Start Site Selection
- PIWI Associated siRNAs and piRNAs Specifically Require the HEN1 Ortholog
- Genome-Wide Patterns of Gene Expression in Nature
- Hypoxia Disruption of Vertebrate CNS Pathfinding through EphrinB2 Is Rescued by Magnesium
- A New Role for Translation Initiation Factor 2 in Maintaining Genome Integrity
- Sex Reversal in C57BL/6J XY Mice Caused by Increased Expression of Ovarian Genes and Insufficient Activation of the Testis Determining Pathway
- The Rac GTP Exchange Factor TIAM-1 Acts with CDC-42 and the Guidance Receptor UNC-40/DCC in Neuronal Protrusion and Axon Guidance
- PLOS Genetics
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- A Coordinated Interdependent Protein Circuitry Stabilizes the Kinetochore Ensemble to Protect CENP-A in the Human Pathogenic Yeast
- Coordinate Regulation of Lipid Metabolism by Novel Nuclear Receptor Partnerships
- Defective Membrane Remodeling in Neuromuscular Diseases: Insights from Animal Models
- Formation of Rigid, Non-Flight Forewings (Elytra) of a Beetle Requires Two Major Cuticular Proteins
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání



