-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaUnifying Genetic Canalization, Genetic Constraint, and Genotype-by-Environment Interaction: QTL by Genomic Background by Environment Interaction of Flowering Time in
Biological traits often display large amounts of genetic variability as well as genetic correlations among traits. This variability provides the raw material for evolutionary change and may alter the direction of trait evolution under selection. Despite this importance, it is unclear whether the genetic controls of variability in single traits and relationships among multiple traits have related mechanisms. Using the flowering time of a plant species as model, here we performed genetic mapping and identified a locus altering single-trait variability and multi-trait relationships. The effect likely results from the distinct thresholds required by its different alleles to trigger flowering, which can be explained by the interaction among this major locus, the variable genomic backgrounds, and the distinct environments. This view is supported by experiments showing epistatic effects of this major locus on flowering time and expression pattern of the candidate gene. Together, our results show that, at least for traits with major signal integrator genes such as flowering time, the genetic control of single-trait variability and multi-trait relationships may have a common underlying mechanism that may be generalizable to other genes or pathways, mediated by interaction among major loci, genomic backgrounds, and surrounding environments.
Published in the journal: . PLoS Genet 10(10): e32767. doi:10.1371/journal.pgen.1004727
Category: Research Article
doi: https://doi.org/10.1371/journal.pgen.1004727Summary
Biological traits often display large amounts of genetic variability as well as genetic correlations among traits. This variability provides the raw material for evolutionary change and may alter the direction of trait evolution under selection. Despite this importance, it is unclear whether the genetic controls of variability in single traits and relationships among multiple traits have related mechanisms. Using the flowering time of a plant species as model, here we performed genetic mapping and identified a locus altering single-trait variability and multi-trait relationships. The effect likely results from the distinct thresholds required by its different alleles to trigger flowering, which can be explained by the interaction among this major locus, the variable genomic backgrounds, and the distinct environments. This view is supported by experiments showing epistatic effects of this major locus on flowering time and expression pattern of the candidate gene. Together, our results show that, at least for traits with major signal integrator genes such as flowering time, the genetic control of single-trait variability and multi-trait relationships may have a common underlying mechanism that may be generalizable to other genes or pathways, mediated by interaction among major loci, genomic backgrounds, and surrounding environments.
Introduction
Elucidating the genetic basis of quantitative traits enables analysis of the processes that shape trait evolution [1]. Two properties that characterize quantitative traits in a population are mean and (co)variance. Most genetic mapping studies focus on loci that influence trait means, while the genomic regions capable of altering trait (co)variances, in contrast, receive relatively little attention despite the crucial role of trait (co)variances in determining the potential for traits to respond to selection [but see 2]. Although researchers have long recognized the importance of genetic control over phenotypic variance [3]–[6], only recently have analyses begun to map genomic regions or genes responsible for trait (co)variance in organisms such as Arabidopsis thaliana [7]–[9], yeast [10], or mouse [11], [12]. In humans, recent studies also have identified variance-controlling loci with biomedical implications [13]–[16].
For a quantitative trait, the phenotypic variation, VP, can be decomposed as VP = VE+VG+VGxE+Ve, where VE is the major environmental variance from different growth chambers or experimental gardens, VG is the genetic variance, VGxE stands for the genotype-by-environment interaction, and Ve is the stochastic noise caused by micro-environmental differences or other factors. For experiments across several different major environments, ‘plasticity’ consists of VE and VGxE. Within the same major environment (where VE and VGxE can be ignored) canalized traits exhibit little phenotypic variation (VP) [6], and causes of phenotypic canalization can be environmental or genetic. That is, one genotype produces a constant phenotype despite environmental variation (environmental canalization reducing Ve), or genetically distinct individuals produce similar phenotypes despite different genetic backgrounds (genetic canalization reducing VG) [6], [17], [18]. Most mapping studies of canalization loci focused on environmental canalization, where the stochastic noise (Ve or similar measures) of inbred lines was often used as a quantitative trait in standard mapping algorithms [7], [9]–[12]; only in a few cases are we aware of attempts to specifically map loci controlling genetic canalization [8], [12]. While Shen et al. [8] identified loci whose alleles differ in the genetic variance among inbred lines (VG), Fraser and Schadt [12] employed separate approaches to map loci controlling genetic canalization and environmental canalization. Here similar to both studies [8], [12], we focus on genetic canalization, which epistatically reduces genetic variance conferred by other genes [4], [6], [17] without changing the extent of molecular polymorphism in the genome. Beyond single traits, in this study we further consider the genetic control of the relationship among multiple traits.
The relationship among traits is often expressed in the form of their genetic variance-covariance matrix, the G matrix [19]. The G matrix of different traits in the same environment indicates the magnitude of potential genetic constraints, whereas the G matrix of the same traits in different environments is algebraically related to the genotype-by-environment interaction component of plasticity (VGxE, sometimes referred to as GxE below) [20]–[22]. While the term ‘genetic constraint’ may be used more broadly for many different combinations of traits (such as the same trait in different ages) [23], here we use this term only to describe the relationship among different traits in the same environment or age. Genetics may control or alter the magnitude of single-trait genetic variance and the size, shape, or orientation of multi-trait genetic covariance structure (genetic constraint or the genotype-by-environment component of plasticity). While to date several studies are available for the genetic mapping of single-trait genetic canalization, few ecologically or evolutionarily important loci controlling trait covariance structure have been investigated, and it is unclear whether these three attributes of quantitative traits (genetic canalization, genetic constraint, and GxE) have related underlying genetic mechanisms.
Because plants often synchronize their phenology with specific environmental conditions [24], flowering time provides a useful model to investigate these attributes. We examined Boechera stricta, an ecological model organism closely related to Arabidopsis [25], [26]. Previously we showed that flowering time is under strong selection in nature [25], and a large-effect phenology QTL (nFT) exhibits trade-offs in flowering probability and fitness across different natural environments [27], [28], providing a good model to investigate the interaction between genetics and environments. Here, using phenological traits in this species, we provide a unifying framework by identifying the same QTL that alters the magnitude of genetic canalization, genetic constraint, and GxE, and proposing that the genetic mechanism likely involves major QTL by genomic background by environment interaction effects. We further test the proposed epistasis effect between major QTL and genomic background on plant phenological traits and candidate gene expression.
Results
Environment-dependent genetic canalization effect
Using recombinant inbred lines (RIL) between B. stricta parents from Colorado and Montana, we performed mapping for loci that affect the among-RIL genetic variance (i.e., genetic canalization) of phenological traits (flowering time and plant size [number of leaves] at flowering) in six different growth chamber environments. We identified three quantitative trait loci (QTL) under the stringent genome-wide significance threshold 0.01 (i.e., the observed Brown-Forsythe value is larger than the genome-wide maximum value from at least 990/1000 permutations) (Table 1, Figure S1). The significance threshold of 0.05 had additional QTL identified, but in this study we only focused on QTL with stronger effects. Two QTL (BST031941 and Bst004238) only had canalization effects on flowering time in one environment (Figure S1, 16 hour days, 25°C, 4 week vernalization; i.e., long days, elevated temperature, short winter). The effects of these two QTL were opposite (Figure S2): the Colorado genotype at BST031941 on linkage group 2 reduced among-RIL genetic variance of (canalized) flowering time, and the Montana genotype at Bst004238 on linkage group 7 caused flowering time canalization.
Tab. 1. List of variance-controlling QTL, the largest-effect marker within each QTL, the Brown-Forsythe statistics, <i>P</i>-value from genome-wide permutation, and proportion of trait variation (<i>V<sub>p</sub></i>) explained by the difference in mean (<i>V<sub>m</sub></i>) or variance (<i>V<sub>v</sub></i>) between two genotypes. 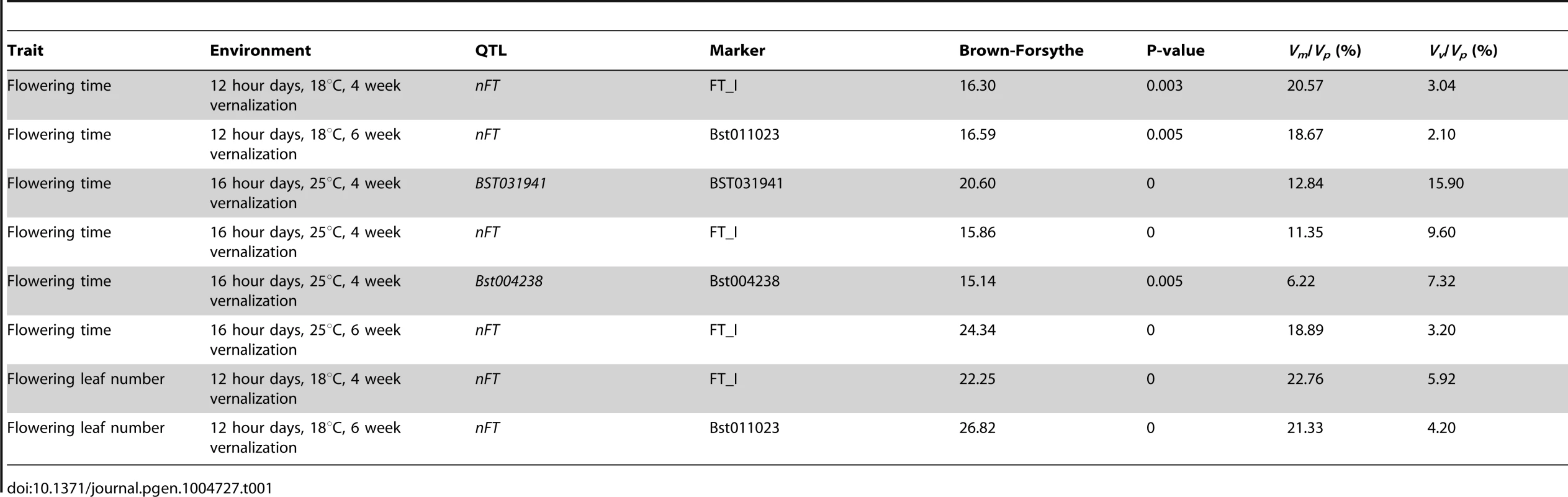
The third QTL, nFT, had widespread canalization effects in multiple environments. This QTL is syntenic with the region containing flowering time gene FT (AT1G65480, hence the name “near FT”) in Arabidopsis thaliana and is a major QTL influencing Boechera stricta phenology, life history and fitness in a broad range of environments [25], [27], [28]. The draft genome assembly from Joint Genome Institute also indicated that the FT gene locates within this region. The canalization effect of nFT was environment-dependent: under the genome-wide significance threshold of 0.01, its effect was significant for flowering time in four environments (both vernalization lengths in 12 hour 18°C and 16 hour 25°C treatments, Figure 1) and number of leaves at flowering in two environments (both vernalization lengths in 12 hour 18°C, Figure S3). For flowering time, ambient environment significantly influenced the canalization effect, but the duration of vernalization did not (Figure 1). Interestingly, the magnitude and direction of nFT's canalization effect depended on the environment (Figure 2). The Montana genotype reduced the among-RIL genetic variance of (i.e., canalized) phenological traits at 12 hour days and 18°C, but the Colorado genotype had this canalization effect in the 16 hour days, 25°C treatment. Although it is known that the existence and magnitude of genetic canalization vary among environments [29], as far as we know, our study may be the first to show that the direction of canalization effect can be reversed between environments (Figure 2).
Fig. 1. Flowering time distributions of families with the Montana (red bars) or Colorado (blue bars) homozygous genotypes of nFT locus in six environments. 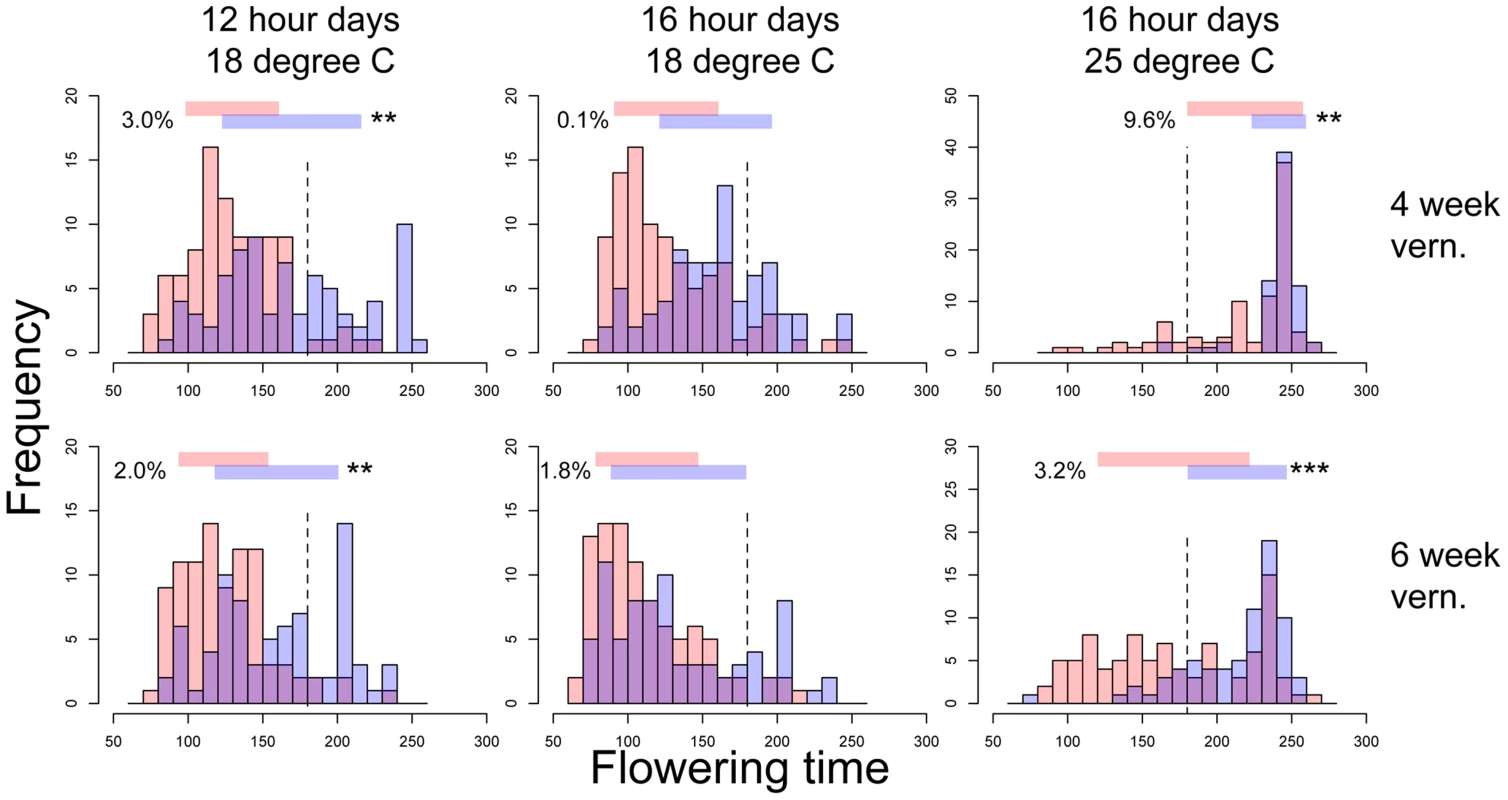
Panels in each column have the same ambient environment: first column – 12 hour days 18°C, second column – 16 hour days 18°C, third column – 16 hour days 25°C. Panels in each row have the same vernalization treatment: first row – 4 week vernalization, second row – 6 week vernalization. Vertical dashed lines (180 days) separate the two growing seasons in each environment. Above each graph, horizontal bars denote the mean plus or minus one standard deviation for each homozygous genotype, numbers on the left denote percent of total variation explained by the difference in variance of the two genotypes, and asterisks on the right denote genome-wide significance of the difference in variance. * P< = 0.05, ** P< = 0.01, *** P< = 0.001. Fig. 2. Distinct canalization effects of nFT locus across six different environments on standardized traits: (A) flowering time and (B) leaf number at first flowering. 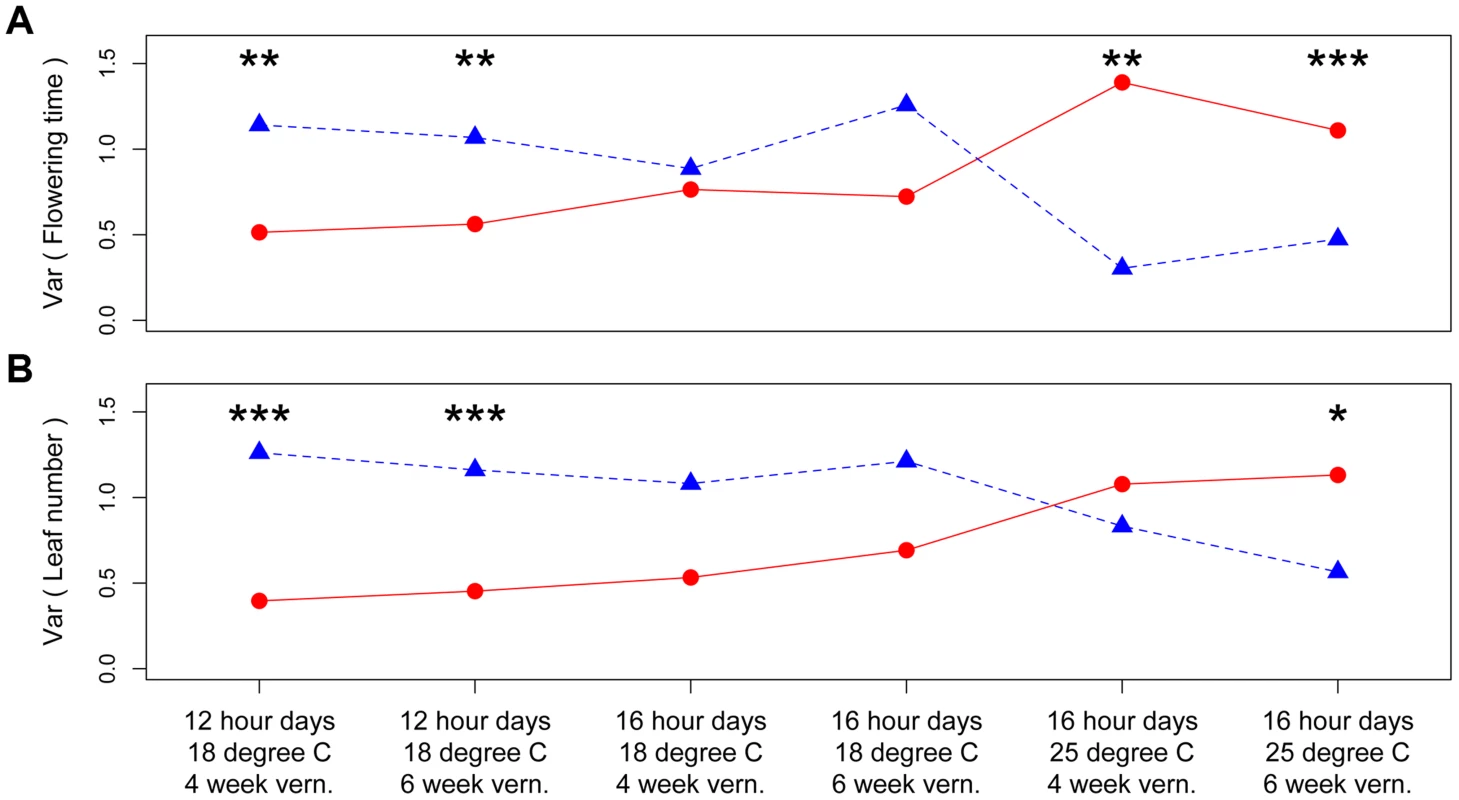
Shown are the genetic variances among families homozygous for the Montana (red dots and solid lines) or Colorado (blue triangles and dashed lines) genotypes. In each environment, asterisks above each genotype pair denote the genome-wide significance of difference in variance. * P< = 0.05, ** P< = 0.01, *** P< = 0.001. Based on these observations, we proposed a ‘threshold hypothesis’ to explain the environment-dependent magnitude and direction of nFT's canalization effect (Figure 3), hypothesizing that the FT gene may be the causal locus within the nFT QTL: In growth chambers, the Montana genotype of nFT accelerated flowering in all environments [25]. In addition to nFT, these recombinant inbred lines also segregate for other flowering time genes in the genome [25]. Since the FT gene within the nFT QTL serves as a hub, which promotes flowering after integrating signals from multiple upstream pathways in the Arabidopsis flowering time network [30], the environment-dependent canalization effect of nFT may be created by the interaction among these factors: 1) different growth chamber environments, 2) distinct genomic backgrounds among RILs created by segregating genotypes of other flowering genes, and 3) the different input-signal threshold needed for either FT genotype to trigger flowering (Figures 1 and 3). For plants in the flowering-promoting environment under long days and cool temperature (16 hour days 18°C, mean flowering time at 4 week vernalization = 141 days, and at 6 week vernalization = 122 days), nFT did not confer a canalization effect because all genomic backgrounds created high input signals for both FT genotypes to initiate flowering. Plants took longer to flower under short days and cool temperatures (12 hour days 18°C, mean flowering time = 147 or 139 days, at 4 or 6 week vernalization, respectively). In these slightly flowering-inhibiting environments, most genomic backgrounds generated lower input signals, which were still enough for the low-threshold Montana genotype to express (predominantly flowering in the first season, within 180 days), whereas a portion of families with the Colorado genotype did not flower until the second growing season because many genomic backgrounds did not generate enough input signals for the high-threshold Colorado genotype (Figures 1 and 3). This resulted in higher variance among nFT Colorado homozygotes, such that Montana was the canalization genotype in these environments. Finally, flowering was significantly delayed at elevated temperatures (16 hour days 25°C, mean flowering time at 4 week vernalization = 229 days, at 6 week vernalization = 190 days). In these flowering-inhibiting environments where most genomic backgrounds generated low input signal, some genomic backgrounds still had enough signal for the Montana genotype to flower in the first season, but some families with Montana genotype flowered only in the second season (Figure 1 and Figure 3). The majority of families homozygous for the Colorado genotype, however, did not flower until the second season due to nFT Colorado genotype's high threshold. Therefore, the Colorado genotype canalized the onset of reproduction in this environment.
Fig. 3. Illustration of the threshold hypothesis, proposing that nFT's reversible canalization effect results from the interaction among FT gene, genomic backgrounds, and environments. 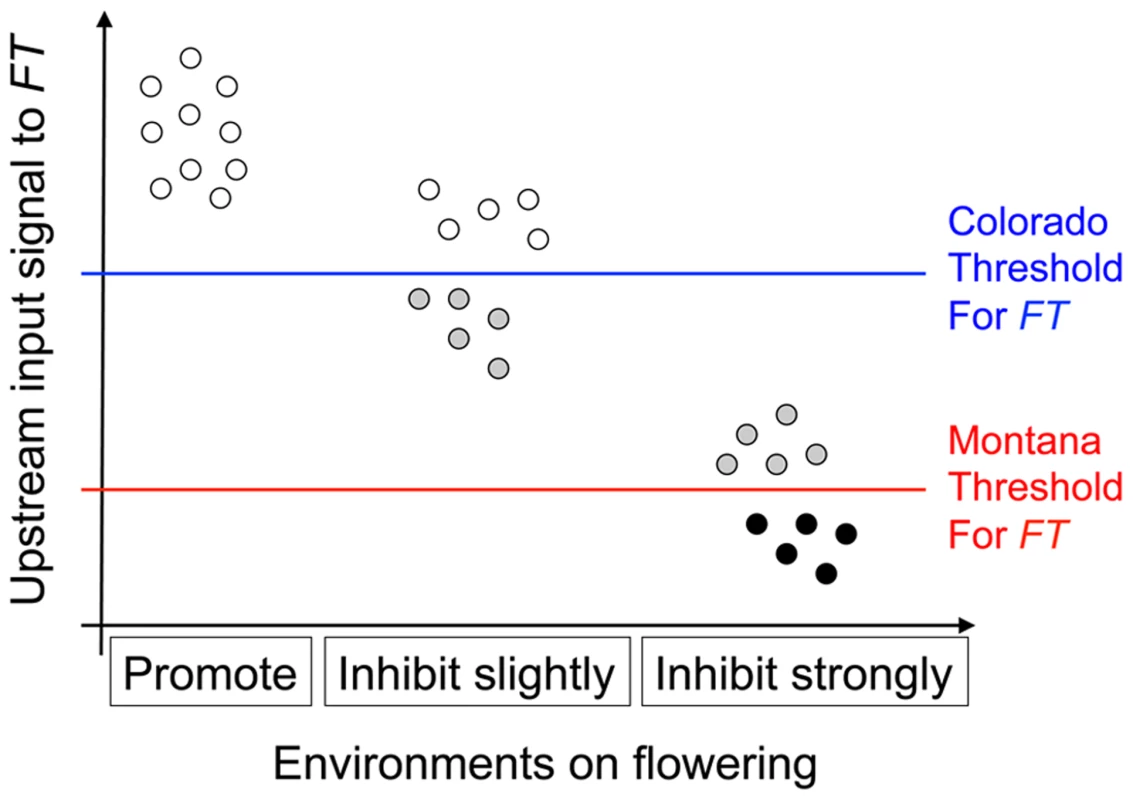
The horizontal axis denotes three different environments: that promotes flowering (16 hour days 18°C), that slightly inhibits flowering (12 hour days 18°C), and that strongly inhibits flowering (16 hour days 25°C). Here, the same set of genomic backgrounds (the ten dots within each environment, representing different combinations of upstream flowering genes) is replicated among environments, generating different amounts of signal input to FT (vertical axis). It is known that the Montana genotype of nFT locus accelerates flowering relative to the Colorado genotype in these growth chambers, therefore the Montana genotype has a lower flowering threshold. Based on the specific environment, a genomic background can generate enough signal for both FT genotypes to express (white dots), only enough signal for the Montana but not the Colorado genotype (grey dots), or not enough signal for either FT genotype (black dots). QTL altering the covariance structure among traits
While genetic canalization concerns the variance of single traits, the covariance structure of multiple traits may also be affected by genetic elements that canalized some traits but not others. The environment - and trait-dependent canalization effect of nFT therefore suggests that it may affect trait covariances (the G matrix; the pairwise genetic correlations were reported in Table S1). Indeed, we identified nFT as the strongest QTL altering the size (Box's M [31]) and orientation (the angle between the first principal component Gmax) of G matrices in different trait-by-environment combinations: flowering time in six environments, leaf number at flowering in six environments, and the combination of all 12 traits (Figure S4). The Krzanowski index method (see Materials and Methods) [32], [33], on the other had, only identified significant nFT effect on the covariance structure of flowering time between the six environments but not for plant leaf number at flowering. In contrast to Gmax angle, the Krzanowski method is likely conservative because it compares the angular difference between subspaces formed by many dimensions, some of which may explain little variation. Figure 4 indicated the difference in size, shape, and orientation between the G matrices from the two nFT genotypes, and the respective trait loadings on each axis were reported in Table S2. Another QTL, BST031941, was also mapped by the Box's M method for the six-flowering-time data set (Figures S4 and S5).
Fig. 4. nFT alters the covariance structure of multiple phenological traits. 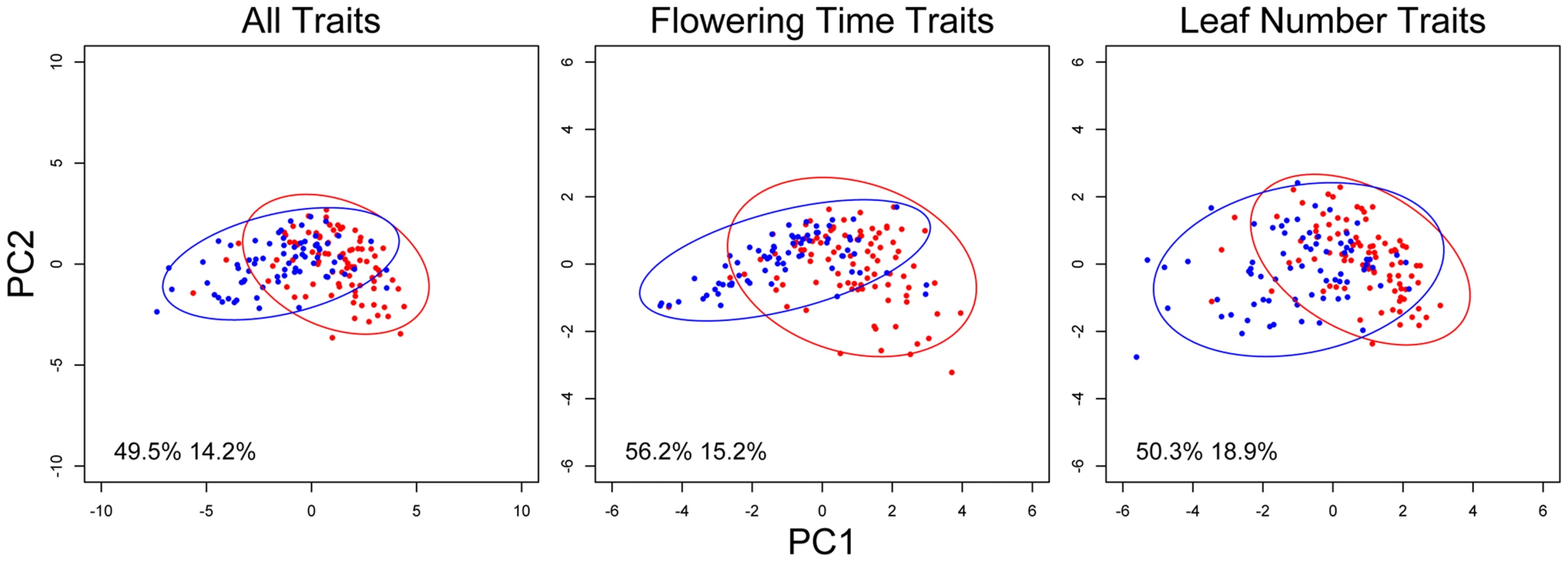
Each dot represents the trait values of one recombinant inbred family, and an ellipse represents the 95% confidence region of the covariance matrix defined by an nFT homozygous genotype. Montana genotype: red dots and ellipse. Colorado genotype: blue dots and ellipse. Numbers in each graph represent proportional variation explained by PC1 or PC2 of all families, respectively. We next mapped QTL controlling the G matrix between flowering time and leaf number in the same environment (indicating potential genetic constraint) and between the same traits in different environments (indicating the magnitude of the genotype-by-environment interaction component of plasticity). Again, nFT and BST031941 were the only QTL influencing most trait pairs. Similar to the canalization result for univariate traits (above), nFT altered the genetic covariance structure between flowering time and leaf number only in both vernalization lengths of two ambient environments: 12 hour days, 18°C and 16 hour days, 25°C, but not 16 hour days, 18°C (Figure 5). The nFT effects, however, were not strong (Figure 5) and only significantly influenced the relative size (Box's M) but not the orientation (Gmax angle) between two G matrices in each case. BST031941, on the other hand, had effects only in environment 16 hour days, 25°C, 4 week vernalization and altered both the size and orientation of the G matrix (Figure S6), consistent with the previous observation that its canalization effect on flowering time only existed in this environment (Figure S1 and S2).
Fig. 5. nFT effect on the structure of covariance between standardized flowering time and leaf number when flowering in each of the six environments. 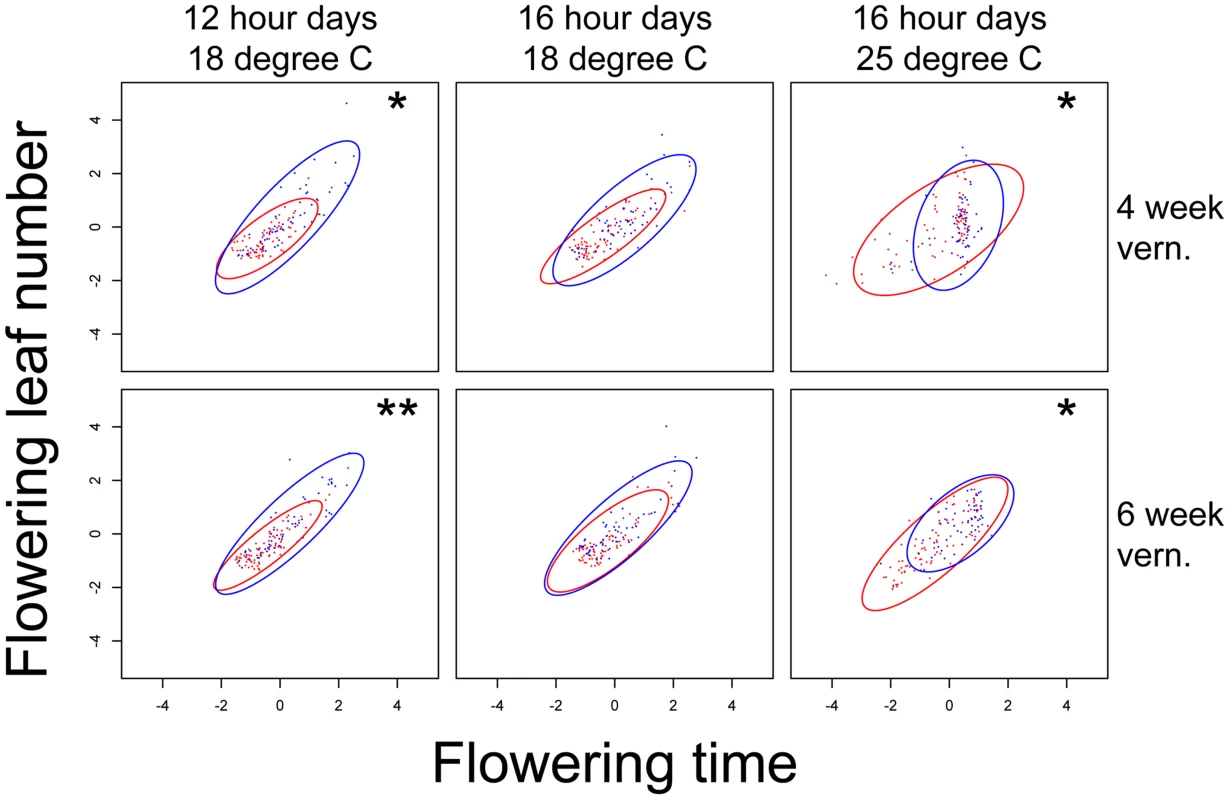
Asterisks on the upper right of each graph denote genome-wide significance for the Box's M method (ellipse size). nFT has no significant effect in the Gmax angle method (ellipse orientation) in any environment. Montana genotype: red dots and ellipse. Colorado genotype: blue dots and ellipse. * P< = 0.05, ** P< = 0.01. Finally, nFT influenced the magnitude of GxE (genotype by environment) interactions (Figure 6). For many trait pairs, nFT had significant effects on both the size and orientation of the covariance matrices, especially in the comparison between chambers 12 hour days 18°C and 16 hour days 25°C, where nFT had significant canalization effect with different directions on univariate traits (Figure 1 and S3). The BST031941 QTL had a significant effect on GxE for flowering time only in the comparison between 16 hour days, 25°C, 4 week vernalization and all other environments (Figure S7). In addition, the G matrices in each comparison differed in both size and orientation. This again is consistent with BST031941's environment-dependent effect described earlier.
Fig. 6. nFT effect on the cross-environment plasticity of standardized phenological traits. 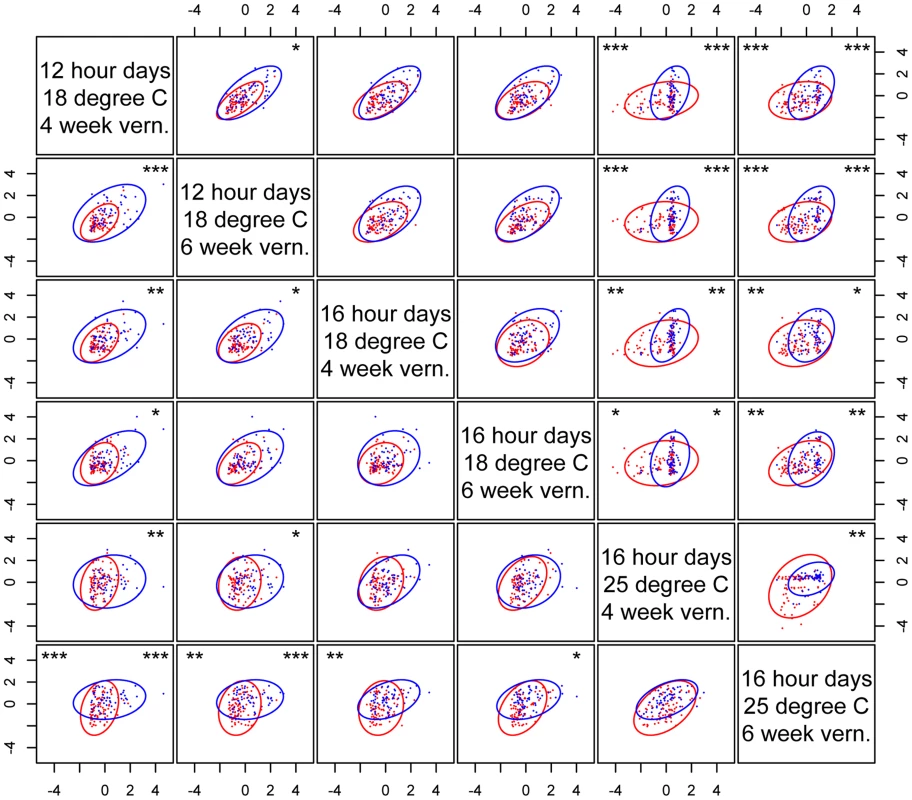
Each graph shows the relationship of the same trait (above the diagonal – flowering time; below diagonal – leaf number when flowering) between pairs of environments. Montana genotype: red dots and ellipse. Colorado genotype: blue dots and ellipse. In each graph, asterisks in the upper right denote genome-wide significance for the Box's M method (ellipse size), and asterisks on the upper left denote genome-wide significance for the Gmax angle method (ellipse orientation). * P< = 0.05, ** P< = 0.01, *** P< = 0.001. nFT epistatic effects in heterogeneous inbred families (HIF)
Since nFT influenced the genetic variance and covariance of phenological traits, we hypothesized that this QTL might interact epistatically with other flowering time genes in the genome and alter the magnitude of their effects, as predicted by our ‘threshold hypothesis’. Our previous study did not identify significant epistatic QTL in these growth chambers [25], nor did our re-analyses identify significant interaction effect between nFT and other QTL (Table S3). These results, however, did not contradict our prediction, since the threshold hypothesis emphasized the interaction between major QTL (nFT) and the cumulative effect from upstream genes (the genomic background), and epistasis between nFT and individual upstream QTL may be too weak to detect in the previous experiment.
To test the epistatic effect between nFT and genomic background, we conducted greenhouse experiments using several heterogeneous inbred families (HIF). Each family had almost identical genomic background and segregated for the two nFT genotypes, and the use of several such families allowed the test for genomic background by QTL epistatic effects (Figure S8). Univariate analyses revealed nFT by genomic background (HIF) interactions for all three traits in the greenhouse environment (flowering time, leaf number and height at flowering, Table 2 and Figure 7 A to C). These effects remained significant after sequential Bonferroni correction. Previously, we detected significant nFT effects on mean flowering time in F6 recombinant inbred lines [25]. Here, analyses in the HIF experiments showed significant epistasis but not main nFT effects on flowering time. This difference likely reflects the complex effects of nFT that depend on genetic background (see Discussion) and is consistent with the idea that the additive effect of a QTL depends on other epistatic genes in the genome [34]. There was, however, a main effect of nFT QTL on height at flowering: Montana homozygotes at nFT are shorter at flowering than Colorado homozygotes.
Fig. 7. Reaction norms showing the nFT by genomic background epistatic effects for three univariate traits (A to C) and three multivariate trait pairs (D to F) in the heterogeneous inbred family (HIF) greenhouse experiment. 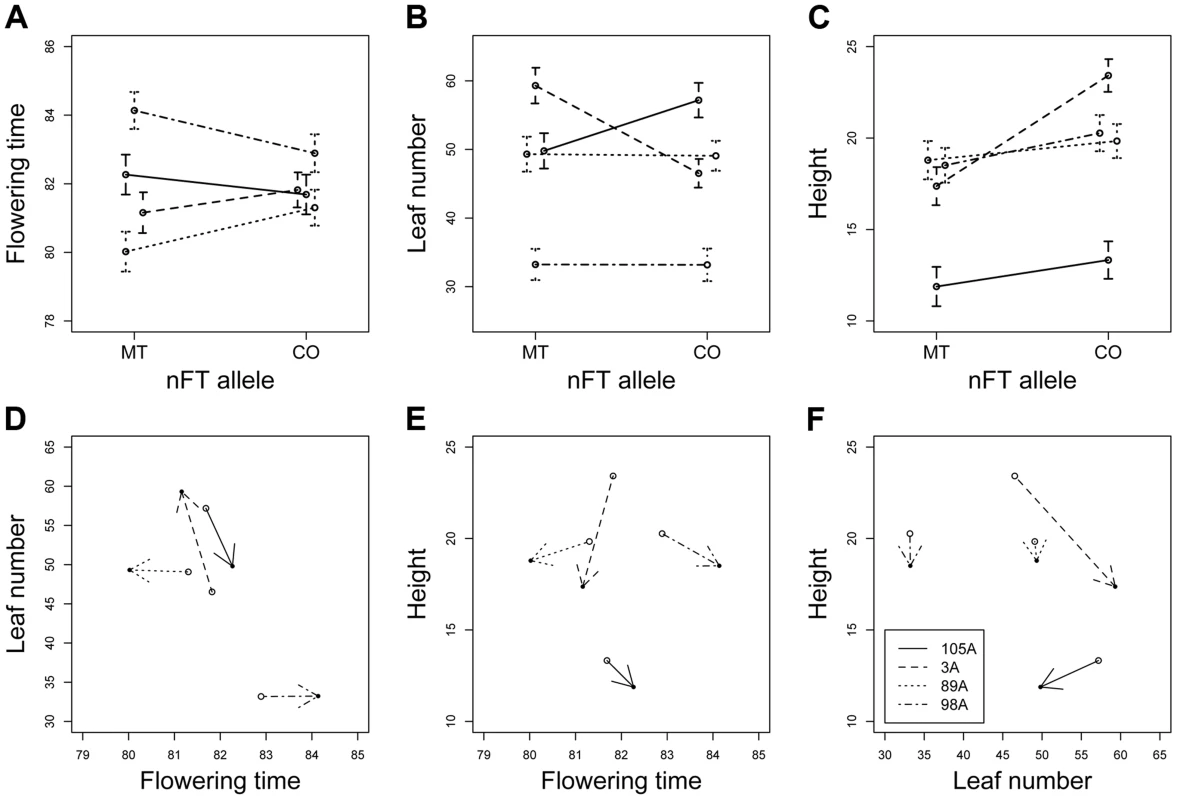
Lines represent the four HIFs and connect the Montana and Colorado nFT homozygous genotypes within each family. Panels A to C show the mean ±1 SE, and epistasis is indicated by the difference in line slopes. In panel D to F, within each family, the arrow points from Colorado to Montana genotype, and epistasis is signified by both the difference in line slopes and arrow directions. Standard error of each nFT genotype within each family is shown in panel A to C and is excluded in panel D to F for graph clarity. Tab. 2. Mixed-model ANOVA for the heterogeneous inbred family (HIF) experiment on phenological traits and FT gene expression in the greenhouse environment. 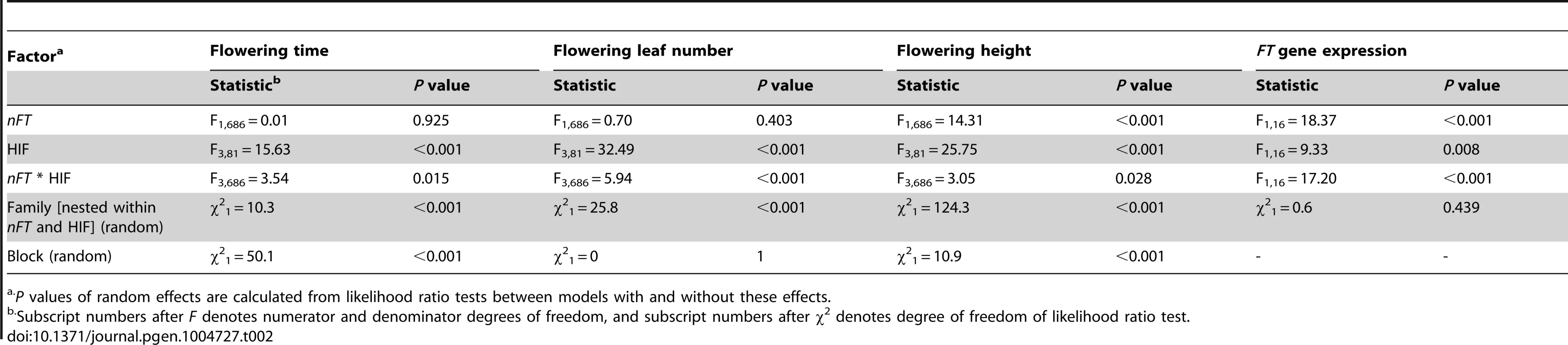
P values of random effects are calculated from likelihood ratio tests between models with and without these effects. In multivariate analysis (MANOVA) simultaneously treating all three traits as response variables, there were significant main effects for nFT (P = 0.024) and genomic background (P<0.001), as well as nFT by genomic background interaction effect (P = 0.005). Figure 7 D to F show nFT by genomic background reaction norms for each pair of traits, demonstrating this epistatic effect.
While our ‘threshold hypothesis’ focused on the effect of the FT gene, the HIF phenotypic experiments only showed effects of the nFT QTL. To further test this prediction that the FT gene interacts epistatically with other flowering genes in the genome, we used the same HIF experimental design (Figure S8) to test the nFT by HIF (genomic background) interaction effect on expression of the FT transcript, using two HIF backgrounds. This interaction effect was highly significant (Table 2). While the Montana genotype had low expression in both genomic backgrounds, the Colorado genotype had significantly higher expression in HIF 98A than in HIF 89A (Figure 8). In HIF 89A, both nFT genotypes conferred low FT gene expression, while in HIF 98A the Colorado nFT genotype conferred higher FT gene expression than the Montana genotype (Figure 8). This observation is consistent with the threshold hypothesis that the genetic variation of other flowering genes in the HIF 89A background does not generate enough input signals for either FT genotype to express. On the other hand, in the greenhouse the HIF 98A genomic background generated enough input signals for the Colorado FT genotype to express but not enough for the Montana genotype. In addition, we found a highly significant association between flowering phenotype (presence of visible flowering buds) and quantitative expression of the FT transcript in individual plants (F1,17 = 9.72, P value = 0.006). This supports that complex trait variation at the nFT QTL may be functionally mediated by the FT locus itself.
Fig. 8. Reaction norms showing the nFT by genomic background epistatic effects for expression level of the FT transcript. 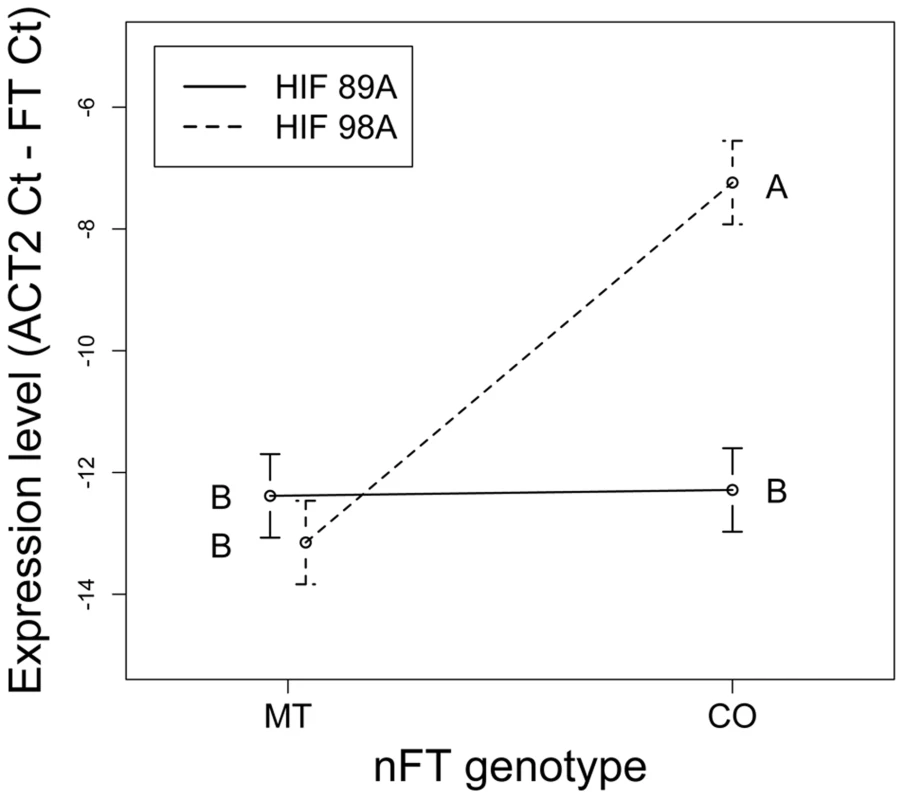
Lines represent the two HIFs and connect the Montana and Colorado nFT genotypes within each family (mean ±1 SE). Epistasis is signified by the difference in line slopes. Capital letters show the contrast between all four nFT genotype – HIF combinations, and FT gene has significantly higher expression in the nFT Colorado genotype with HIF 98A genomic background. Discussion
The genetic basis and evolutionary history of canalization in one trait, genetic constraint among multiple traits, and genotype-by-environment interaction (GxE) across different environments are active foci for research in evolutionary genetics [2]. While many genetic mapping studies are available for single-trait canalization, the majority concerned environmental canalization [7], [9]–[12], and only in a few studies are we aware of mapping for genetic canalization [8], [12]. Here we used similar approaches to previous studies for single-trait genetic canalization [8], [12], but extended our analysis beyond single traits and focused on the QTL altering trait covariance structures. We provide a unifying framework for these mechanisms in the flowering time of B. stricta by showing how one QTL (nFT, which contains the floral integrator gene FT) influences all three attributes for phenological traits of Boechera stricta. nFT influences single-trait genetic canalization, and the magnitude and direction of its effects can be reversed across environments. nFT's environmentally dependent and reversible effect in one trait, when extending to multiple traits, creates the distinct patterns of covariance structure among different traits in the same environment (altering the magnitude of genetic constraint) or among the same traits in different environments (altering the magnitude of GxE). We propose a ‘threshold hypothesis’ (see Results and Figure 3) to explain this pattern, and the hypothesis is supported by the significant nFT by genomic background epistatic effects on phenological traits and transcriptional variation of the candidate FT locus in the heterogeneous inbred family (HIF) experiment, echoing studies showing the prevalence of epistasis in both trait and molecular evolution [34]–[41].
The threshold hypothesis
In this study we proposed a ‘threshold hypothesis’ to explain the environment-dependent genetic canalization effects of nFT on flowering time, and the concept is illustrated in Figure 3. This hypothesis focuses on three components of flowering time regulation: the downstream floral signal integrator gene FT, the genomic backgrounds with different combinations of polymorphic upstream genes (each generating small input signals to FT), and multiple growth chamber environments that also generate different levels of input signals. In this hypothesis, the activation of FT expression (which then triggers flowering) depends on whether the upstream input signals, which vary with different combinations of genomic backgrounds and environmental stimuli, exceed the genotype-specific threshold of FT. The interaction among major threshold gene, genomic backgrounds, and environmental stimuli therefore triggers the environment-dependent canalization effect of flowering. The threshold model may also help explain how discrete and large-effect phenotypic changes may be caused by continuous and small-effect upstream genetic mechanisms.
In this simple threshold hypothesis, the effect of the genomic background on the initiation of FT expression is binary: input signals generated by different backgrounds or environments are either below or above the threshold for FT alleles to express. In a previous study of Arabidopsis thaliana, Welch et al. [42] used sigmoid functions to model genes in the flowering time pathway. These sigmoid functions model the relationship between quantitative upstream input signals and the response of downstream genes, and these models can be viewed as the quantitative generalization of our threshold hypothesis (see details in Figure S9). While in Welch et al. [42] the wild-type allele of each gene was assigned a sigmoid function and knockouts always have zero output, in our case the two FT alleles with different thresholds simply have different response curves (Figure S9). The threshold hypothesis is therefore supported by previous studies and may be applied to genes or networks that can be modeled with continuous functions.
Our threshold hypothesis also echoes the recent idea that cryptic genetic variation (CVG) is not ‘mechanistically special and mysterious’ [43], but instead that genetic effects are conditional on other genes (epistasis or dominance) or on the environment (GxE), and CVG can be viewed as ‘conditionally neutral genetic variation’ [43]. It is worth emphasizing that the mechanism underlying genetic canalization effects of nFT and the well-known heat shock protein 90 (Hsp90) [29], [44] may be different. Hsp90 has a specific function as a protein chaperone [45]–[47], whose expression pattern may be independent of the proteins it helps folding. On the other hand, expression of the FT gene is trigged by signals from upstream genes. As a consequence, we predict that distinct input-signal requirements for FT's different genotypes may generate QTL by genomic background interaction effects on phenological traits and on its own expression pattern, which is supported by our HIF experiments. Therefore, in contrast to Hsp90, whose specific function may not easily be extrapolated to most genes or pathways, our threshold hypothesis and the case of the FT gene in the flowering time pathway may represent an alternative mechanism for other cases of canalization, genetic constraint, and genotype-by-environment interaction in traits with major signal integrators such as flowering time.
In fact, a similar idea has been proposed and tested previously [48]–[50]. Siegal and Bergman [48] modeled the effect of biological networks on trait canalization and showed that canalization is ‘an inevitable consequence of complex developmental-genetic processes’ that does not require the force of stabilizing selection or a specific molecular function such as Hsp90. Further studies supported this model by showing that gene knock-outs can affect both genetic and environmental canalization of yeast gene expression [49] as well as phenotypes [50]. More importantly, they showed that ‘capacitors’ (canalization genes) are more likely to be network hubs [50], like the FT gene in this study. While these previous studies focus on artificial gene knockouts, here we provide an example of trait canalization from natural variation for ecologically important traits.
Different from other modeling studies, in this study our example of the threshold hypothesis separates the growth chambers into three categories (flowering promoting, slightly inhibitory, and strongly inhibitory) instead of by specific environmental factors (day length, ambient temperature, or vernalization length). For flowering time, pathways responding to different environmental signals converge at floral signal integrator genes such as FT, the current focus of the threshold hypothesis, and therefore it is more straightforward to classify environments based on their effect on flowering promotion (the horizontal axis in Figure 3). This is analogous to studies that classify research sites by their effect on plant growth or crop yield [51] and allows modeling flowering time variation without addition information on the expression of upstream genes. We recognize that the threshold hypothesis represents a simplification of the underlying continuous biological process into a qualitative factor (whether plants flower in the first season or not), and future work may explicitly consider the effect of individual environmental factors to allow detailed quantitative modeling of flowering time.
nFT controls univariate trait genetic variance
The link between epistasis and genetic canalization of flowering time has been established in the model plant Arabidopsis thaliana. Stinchcombe et al. [52] observed that the latitudinal cline in flowering time only exists in genotypes with the wild-type functional allele of FRIGIDA but not for the deletion allele (FRIΔ), and the flowering time of accessions bearing the deletion allele is canalized. This canalization effect is caused by epistasis between FRIGIDA and FLC [37], where the canalizing FRIΔ allele suppressed the effect between different alleles of FLC. Similarly, in our study we identified nFT as the canalization locus and demonstrated the epistatic effects in the HIF experiment, where the different nFT genotypes alter the phenotypic effect of different genomic backgrounds (specific allelic combinations of other flowering genes). In addition, as in other cases of canalization genes [29], we also find that nFT's canalization effect depends on the environment.
The adaptive value of canalization has received considerable attention [5], [6]. Theoretical analyses have modeled the conditions under which canalization will evolve [17], [53], [54] (but see [48]–[50]), and empirical studies in Drosophila have shown that traits with higher fitness effects have greater canalization [55], [56]. Rutherford et al. [29] suggested that the wild-type canalizing allele of Hsp90 gene in Drosophila may be favored because it buffers against potentially unfit background genetic variation. On the other hand, the non-canalizing allele might be favored when a trait is under directional or disruptive selection. Under both scenarios, however, the allelic polymorphism in canalization genes will be eliminated if trait canalization is universally favored or disfavored by natural selection. Our results provide a mechanism where the polymorphism of canalization genes can be maintained. Because which nFT genotype has the canalization effect depends on specific environments, different genotypes may be favored under distinct environments even with consistent natural selection for or against trait canalization, beyond mutation-selection balance [17]. For example, if natural selection favors flowering time canalization, in populations under 12 hour days 18°C the Montana genotype would be favored, and the Colorado genotype would be favored under 16 hour days 25°C because they are the canalization genotypes in these respective environments.
The environmental dependence of nFT canalization may also maintain the molecular polymorphism of other flowering genes in the genome. Canalization may change the selective influence on other genes by suppressing the genetic variation expressed in traits [18], [57]. In the case of heat shock protein 90 (Hsp90), the wild type allele buffers the phenotypic effect of potentially deleterious mutations in the genome, thereby reducing the force of purifying selection on these mutations [29], [44]. The accumulation of cryptic molecular variation in the genome may provide additional evolutionary potential [18] once the canalization effect is disrupted. The case of Boechera stricta flowering time, however, may be more complex due to the nFT by environment interaction effect on canalization. Even if the selection force on flowering time is identical across populations, other flowering loci in the genome may still be subject to different types and magnitude of natural selection depending on local environment and nFT genotype. Such variation in selection may in turn influence the molecular polymorphism of other flowering time genes.
In this study, flowering time was defined as the days elapsed since initial vernalization, excluding the duration of the second vernalization for plants that did not flower in the first growing season. Since the time of vernalization simulated ‘winter’ conditions with little plant growth, this approach quantifies the number of growing-season days the plants experienced before first flowering. Our results and the threshold hypothesis suggest that the canalization effect primarily reflects whether plants flowered in the first growing season, and therefore this approach captures both the variance between and within seasons. In addition to flowering time, the nFT locus also influenced the (co)variance of ‘leaf number when flowering’, a well-defined quantitative trait often used as an indicator of the reproductive phenology. We therefore think these phenological traits reflect important underlying biological processes.
nFT controls multivariate trait covariation
The covariance structure among multiple traits (G matrix) indicates the magnitude of potential genetic constraints and can have profound effect on the magnitude and direction of trait evolution under selection [3], [58]–[60]. While many methodological and empirical studies have compared the G matrix evolution among evolutionary lineages [e.g., 3], only a few studies have investigated the genetic mechanism or identified the genomic regions responsible for this G matrix difference. In Arabidopsis, Stinchcombe et al. [61] found that two alleles of the ERECTA gene confer different structure of the G matrix among four traits. In mice, Wolf et al. [62] also identified significant epistatic pleiotropy effects of QTL on the covariance between traits. Both examples investigated the change of covariance structure caused by candidate loci, and to our knowledge, our study may be one of the first attempts at genome-wide mapping of QTL altering the covariance structure among multiple traits.
In addition to canalization in single traits, we have identified nFT as the major QTL altering the genetic covariance structure in both multivariate trait combinations: 1) between different traits in the same environment (indicating the magnitude of genetic constraint), and 2) the same trait between different environments (indicating the magnitude of GxE, the genotype-by-environment interaction component of plasticity). This supports the idea that genetic constraint and plasticity are related concepts [63] and can be connected by trait - or environment-dependent canalization: When one trait is canalized but another is not, the magnitudes of genetic constraint or GxE are altered [55]. For example, considering the relationship between flowering time and leaf number at flowering under 16 hour days, 25°C, 4 week vernalization, the nFT Colorado genotypes canalize flowering time, but there is no nFT canalization effect for leaf number (Figure 5). This changes the orientation of covariance structure by ∼35°. For GxE, the nFT Montana genotype canalizes flowering time in 12 hour days, 18°C, 4 week vernalization, and the Colorado genotype canalizes flowering time in 16 hour days, 25°C, 4 week vernalization. This leads to a significant difference in the orientation of the G matrices for the two nFT genotypes (∼59°, Figure 6, row 1, column 5). Therefore, it is helpful to view the multi-trait covariance structure as a multivariate extension of single-trait variance, and our result supports the idea that the change of magnitude in genetic constraint or GxE may be a consequence of trait - or environment-dependent canalization effects [64]. Our results also suggest that, in a threshold-like gene regulation system, the change of trait genetic covariance structure may be achieved simply by the shift of the gene activation threshold (Figures 3 and S9).
As described in the Introduction, plasticity consists of VE and VGxE. In this study we showed that the nFT QTL altered the magnitude of VGxE. It is also possible that genetic mechanisms altering VE exist. With this genetic mechanism (here termed macro-environmental canalization, as opposed to micro-environmental canalization which concerns Ve, the variance from stochastic noise), one genotype of the QTL may exhibit similar phenotypes across diverse environments while the other genotype has varying phenotypes. While we did not specifically map for this macro-environmental canalization, the genetic mechanism altering VE may also be realized from the threshold hypothesis (Figure 3): consider the flowering time under two hypothetical environments, one strongly promotes flowering (‘ENV1’ hereafter: all genomic backgrounds generate signal above the Colorado threshold – all dots are white in Figure 3) and the other has effect between ‘slightly inhibiting’ and ‘strongly inhibiting’ (‘ENV2’ hereafter: all genomic backgrounds generate input signal above Montana but below the Colorado threshold – all dots are grey in Figure 3). Given the low threshold of the FT Montana genotype, all genomic backgrounds flower in both environments, and the VE for the Montana genotype is low. For the Colorado genotype, however, all genomic backgrounds flower under ENV1 but none flowers in ENV2, and VE is large for the Colorado genotype. Therefore, although in terms of upstream input signals the VE stays the same regardless of FT genotypes, for flowering time FT may control macro-environmental canalization due to the threshold-type reaction to upstream signals. This also suggests that environment-dependent genetic canalization, macro-environmental canalization, and the alteration of the magnitude in GxE may represent different viewpoints of the same concept.
HIF experiment and the effect of nFT
Results from the HIF experiment show strong nFT by genomic background epistatic effects on phenological traits and on expression of the FT locus, demonstrating: 1) nFT's role as an epistatic modifier of other flowering genes and 2) the effect of other flowering genes (different HIF genomic background) on gene expression of the FT locus itself, a network hub integrating signals from upstream genes in the flowering time pathway. These observations are consistent with the ‘threshold hypothesis’ illustrating how flowering pathway function can generate epistasis between FT and other flowering genes (Figure 3) and also echo studies with gene by genomic background epistatic effects in the flowering time pathway of Arabidopsis [65]. Unlike the strong and direct epistatic relationship between Arabidopsis flowering genes FRIGIDA (FRI) and FLOWERING LOCUS C (FLC) [37], [66], FT responds to the combined effect of multiple upstream pathways, and the one-to-one epistasis between nFT and individual flowering time loci may be too weak to be detected by our previous [25] or current study (Table S3). Our novel algorithm to map (co)variance QTL therefore serves as a valuable alternative to standard pairwise searches for epistasis, paralleling recent developments in human genetics [15], [67]. In the flowering time of B. stricta, this epistatic relationship between nFT and genomic background has been supported by our HIF experiment.
In this study we employed a linkage mapping approach to map (co)variance QTL, and the issue of sample size and statistical power may be a limitation [68]–[70]. We recognize that the experimental design may not have sufficient power to detect all QTL, especially those with minor effects. This limitation, however, does not affect the significant functional variation at nFT. Although it might be possible that the nFT QTL's effect on trait mean, variance, and covariance structure are effects of several closely linked genes, our threshold hypothesis and following HIF experiments both suggest that the FT gene may exhibit these pleiotropic effects: being a floral signal integrator, the two FT alleles may influence trait means due to different thresholds for activation by upstream signals (which predicts and is supported by our results that the two alleles vary in gene regulation patterns instead of amino acid substitutions). Such threshold differences may interact with various genomic backgrounds or environmental stimuli and thus alter the pattern of trait (co)variation (see Results and Figure 3). Further, it is not uncommon that genes or QTL can simultaneously control trait means and (co)variances, as previous studies mapping canalization loci have identified QTL or genes known to control trait means [7]–[10], and a recent study has shown strong genetic correlation between developmental instability (environmental canalization) and phenotypic plasticity [71]. Taken together, these results suggest that, at least in traits with major signal integrators such as flowering time, the control of trait means, (co)variances, and genotype-by-environment interaction may have a similar genetic basis.
Materials and Methods
Recombinant inbred line (RIL) data
All RIL data were obtained from our previous study [25]. Briefly, a cross was made between one genotype from Montana and one from Colorado [72], and F6 RIL were generated through self-pollination and single seed decent. From each family, one F6 individual was genotyped at 164 polymorphic molecular markers, with an average spacing of 5.5 cM between neighboring markers. The F6 RILs were predominantly homozygous (95.9%). Heterozygous genotype calls in any marker of any family were treated as missing data.
In the previous study, we measured flowering time and leaf number at flowering (N = 5 individuals/RIL/treatment and N = 35 individuals/parental line/treatment) in six distinct environments, composed of two vernalization lengths (four or six weeks) at 4°C and three growth conditions (12 hour days 18°C, 16 hour days 18°C, and 16 hour days 25°C). In this study, we analyze family mean trait values for the 178 RIL and 2 parental lines obtained from the previous study [25]. The growth chamber experiments consisted of two growing seasons. Individuals that had not flowered within 180 days after the first vernalization were subject to another 6-week vernalization. In addition, during the second growing season, plants from the 16 hour days 25°C chambers were moved to 16 hour days 18°C [25]. Two traits from each growing condition were used in this study: flowering time and leaf number at the time of first flowering. Flowering time is defined as the number of elapsed days since the end of the first vernalization, and the 6-week period of the second vernalization was excluded from the flowering time estimation. All traits were standardized to a mean of zero and standard deviation of one before further analysis.
QTL controlling variance of single traits
For each genetic marker, we used the Brown-Forsythe test, a modification of Levene's test based on median, to estimate the difference in trait variance between the Colorado homozygote and the Montana homozygote at markers across the genome. This approach is similar to Shen et al. [8] and can detect QTL responsible for genetic canalization. We determined the statistical significance by the genome-wide permutation method of Churchill and Doerge [73]. One thousand permuted datasets were generated by randomizing trait values with respect to marker genotypes. The marker-trait relationship was randomized, but the genotype vector and the trait vector for each individual were not altered. From each permuted data set, the Brown-Forsythe statistic was calculated at each genetic marker, and the genome-wide maximum Brown-Forsythe value was recorded, providing a genome-wide null probability distribution. The P-value of the Brown-Forsythe statistics for each marker in the observed data was obtained by comparing this value to the null distribution of Brown-Forsythe values from the 1,000 randomized datasets. Our genome-wide permutation procedure provides a straightforward control for multiple tests across all markers and is also robust to violations of the assumption of multivariate normality. The estimation of variance and covariance, however, may be limited by small sample size, perhaps resulting from missing data or segregation distortion. To prevent possible bias, we therefore excluded six markers with minor allele frequency less than 0.33. All computations were performed in R (http://www.r-project.org/) using scripts available upon request from CL.
Considering the effect of a QTL, the total trait variation (Vp) can be decomposed into:
where Vm is the variation explained by the difference in mean of the two homozygous genotypes, Vv is the variation explained by the difference in variance of the two genotypes, and Vr is residual variance arising from other sources [8]. For each significant QTL, we calculated the proportion of variation explained by Vm and Vv, following previously published equations designed for populations with two homozygous genotypes in each SNP [8]: where p and q are the genotype frequencies of the Colorado and Montana homozygotes, respectively. μCO and μMT are the mean, and σCO and σMT represent the standard deviation of the Colorado and Montana homozygotes.QTL controlling the structure of covariance matrix among multiple traits
Here we aim to map QTL altering the covariance structure of three groups of traits: 1) flowering time and plant size at flowering (number of leaves) in all six environments (G matrix with 12 traits); 2) flowering time in all environments (G matrix of six traits); 3) plant leaf number at flowering in all environments (G matrix with six traits). We further mapped QTL changing the covariance structure between flowering time and plant size at flowering separately for each environment (representing the magnitude of genetic constraint) and between the same trait in pairs of different environments (representing the magnitude of the genotype-by-environment interaction component of plasticity, GxE). Among the multiple ways to model plasticity (reviewed in [20], [74], here following Falconer [21]), we treat the same trait in distinct environments as separate traits and model their covariance structure. We choose this definition because this view generalizes both GxE and genetic constraint into the relationship among traits, allowing the use of established methods for G matrix comparisons.
For each molecular marker, we separated the data into two groups of homozygous genotypes. Two separate (co)variance matrices (G matrices) were estimated, and we assessed the QTL effect by comparing the G matrices via three methods: 1) Box's M statistics; 2) the angle between Gmax; 3) the Krzanowski index. Statistical significance is determined by the genome-wide permutation algorithm described above. We acknowledge that the covariance matrix estimated from family means may not be identical to the genetic covariance matrix estimated from individual-level mixed-model MANOVA. This simplification, however, was necessary to ensure computational feasibility since the G matrices needed to be calculated twice (one for each homozygous genotype of a marker) for ∼160 markers for each of the 1,000 permuted data sets.
Box's M statistic [31] compares the difference between the trace of multiple covariance matrices and the trace of their pooled covariance matrix:
where g is the number of matrices to be compared (two in our case), Vi is the degrees of freedom, and Si is the trace of the i-th matrix. N, the overall degrees of freedom, is the sum of all Vi values. The trace, S, of the pooled covariance matrix is: Since the trace of a covariance matrix is the sum of its diagonal elements and is equal to the sum of eigenvalues from its principal components, the Box's M value could be interpreted as the difference between the multivariate volumes occupied by different covariance matrices. In our case, the Box's M method compares the overall size of G matrices from the two genotypes at each genetic marker. Traditionally the significance is determined by an F-test and is sensitive to deviations from multivariate normality, but our genome-wide permutation procedure alleviates this parametric distributional requirement.Two covariance matrices could differ not only in size but also in their orientation. We used two methods to compare the orientation between G matrices [32], [75]. To estimate the radian angle between the respective Gmax (first principal component), we first calculated the angle between the first eigenvector, u and v, of the two G matrices respectively:
where the dot symbol calculates the dot product between vectors. Since eigenvectors are directional, θ may be larger than π/2 (90 degrees, the maximum possible angular difference between two non-directional axes). Therefore if θ is larger than π/2, the radian angle between Gmax is calculated as π - θ, otherwise the angle equals θ. This method estimates the angular difference between the respective axes with most variation in each G matrix.The Gmax method, however, has a caveat that when G matrices have many dimensions (traits), other principal components may carry substantial amounts of variation, and comparing Gmax may not be sufficient [32]. Therefore, we employed the method of Krzanowski [33], which has also been used in recent studies [32]. In brief, this method compares the k-dimensional subspace between two G matrices, where k is less than or equal to half of the dimension of the original G matrix. For example, in a data set with 10 traits, we estimated the degree of similarity between two subspaces formed by the first five eigenvectors of two G matrices. Similar to the Gmax method above, each eigenvector w that will be used in the analysis was first standardized by the square root of its dot product:
The ‘matrix of similarity’ (S) then is calculated as: where A and B are matrices containing the first five standardized eigenvectors of the two respective G matrices, and superscript T denotes matrix transpose. As in other studies [32], we used the sum of eigenvalues of this S matrix (the Krzanowski index) as a measure of overall similarity between the two subspaces. This index ranges from 0 to 5 in our example of 10 traits, with 0 signifying non-overlap and 5 indicating total overlap between subspaces. For our purpose of mapping QTL whose different genotypes confer the most dissimilar G matrices, we compared the negative Krzanowski index of each marker to the 1,000 maximum negative Krzanowski indexes from permutation.In summary, while the Gmax and Krzanowski methods compare the orientation of linear relationship among traits, Box's M tests the dispersion of points from this linear relationship. All mapping algorithms were written in R (http://www.r-project.org/). When only two traits are involved, the angle between Gmax captures all the difference in orientation between G matrices, and therefore the Krzanowski method is not necessary.
Heterogeneous inbred family phenotypic experiment
To test the existence of epistasis as predicted by the threshold hypothesis, we performed analysis of variance for the interaction effect between nFT and other flowering time QTL identified in the same growth chambers from our previous study [25]. The epistatic effects of other QTL were tested separately, using flowering time as response and nFT, the other QTL, and their interaction as fixed-effect predictor variables in each model.
We generated four heterogeneous inbred families (HIFs, Figure S8) to test the epistatic effect between nFT and genomic background (the cumulative effect of other genes in the genome). Based on the genotype data in the F6 generation [25] we identified four F5 parents heterozygous at nFT and mostly homozygous at other markers. From each F5 parent we planted approximately 250 seeds, which are self-full siblings of the original genotyped F6 individual in Anderson et al. [25] (N = 1097 plants total from four F5 parents). We genotyped the microsatellite marker C02 [∼5 cM from the FT gene,25] in all plants and collected seeds from those that were homozygous at C02. Seeds from the same F6 individual (a ‘family’ hereafter) have virtually identical genomic composition. All plants within the same HIF are nearly identical in other genomic regions but segregate for two nFT homozygous genotypes. With four HIFs that are different in genomic background, the interaction between nFT genotype and HIF (genomic background) provides a statistical test for epistatic effects on phenology.
The HIF experiment was conducted in the Duke University Greenhouse rather than in multiple growth chamber environments as in the RIL experiment. To provide independent replication for each homozygous nFT genotype, we selected at least 20 homozygous families from each HIF (24 families from HIF 3A; 22 families from HIF 89A; 23 families from HIF 98A; and 20 families from HIF 105A), for a total of 89 families. In November 2011 we place 10–15 seeds from each of the 89 families on moist filter paper in petri dishes in dark conditions at ambient temperature for 3 weeks until germination. As in other B. stricta greenhouse experiments [76], seedlings were then planted in Ray Leach SC10 ‘Cone-tainers’ (21 cm in depth and 3.8 cm in diameter, Stuewe & Sons Inc., Tangent, OR, USA), with the lower 80% of each Cone-tainer filled with Fafard 4P Mix soil (Conrad Fafard, Agawam, MA, USA) and top 20% with Sunshine MVP soil (Sun Gro Horticulture, Vancouver, BC, Canada). Greenhouse conditions were as follows: 16-hour days (6 AM to 10 PM), diurnal temperature of 18–21°C, and nocturnal temperature of 13–16°C. We used a random number generator to assign seedlings to distinct positions in 9 blocks, each containing 91–96 plants. Each block included individuals from all HIFs and most families from each HIF (In some cases, a family did not have enough siblings to be represented in each block). The blocks were rotated around a greenhouse bench once a week to minimize the effects of environmental gradients in the greenhouse.
In January 2012, all rosettes were vernalized at 4°C for 8 weeks. Plants were removed from vernalization on 29 February 2012, at which point we monitored them 7 days/week and recorded the date of first flowering as well as the number of leaves and plant height at first flowering. By April 23, 2012, we had collected phenological data from 8–10 full siblings per family (N = 785 F7 individuals flowered successfully). No individuals flowered after that date. Relevant data are available in Dataset S1.
Statistical analysis was performed with REML mixed-model ANOVA (Proc Mixed, SAS 9.3, SAS, Cary, NC). We first conducted a multivariate ANOVA (MANOVA) to address how the three response variables (day of first flowering, plant height and number of leaves at flowering) varied with HIF (3A/89A/98A/105A), nFT genotype (Montana/Colorado homozygote), and nFT by HIF interaction (all are fixed effects). We incorporated ‘family’ (nested within nFT homozygote, cross-classified with HIF) and block as random effects. We then conducted univariate ANOVA for each response variable with the same statistical model.
FT gene expression in HIF
The contrasting canalization effect of the nFT locus in different environments suggests a three way interaction of the major QTL (nFT) by genomic background (the combination of other flowering-related genes) by environment conditions, and the interaction between nFT and genomic background on phenological traits is tested in the HIF experiment. The nFT locus contains the ortholog of the FT gene in Arabidopsis (AT1G65480). FT serves as a major hub for integrating upstream signals of flowering, and its expression often correlates with the onset of flowering [30]. If the variation in the FT gene in Boechera stricta is responsible for the differential canalization effect of the nFT QTL in our Montana by Colorado cross, its expression pattern should vary depending on the nFT genotype and genomic background. We therefore test the expression pattern of FT in the same HIF experimental design.
Two HIFs (HIF 89A and HIF 98A) were used in this experiment. Within each HIF we obtained five families from each homozygous nFT genotype for a total of 20 families. Forty experimental plants (two individuals from each family) were completely randomized, and all planting procedures and greenhouse environmental settings were as above. Rosettes were grown in the Duke greenhouse for 12 weeks and stratified at 4°C for 8 weeks. In Arabidopsis, FT mainly expresses in leaves, where protein translation happens, and the proteins are transferred to floral meristems [77]. We therefore collected one young leaf from each plant four weeks after vernalization ended. FT in Arabidopsis exhibits circadian rhythm in gene expression, and under 16-hour days, its maximum expression is in the end of daytime [78]–[80]. We therefore collected leaves from all 40 experimental plants around 10 pm, when the 16-hour Duke greenhouse days end. Leaves were immediately flash frozen in liquid nitrogen and stored at −80°C. RNA was extracted with Sigma Spectrum Plant Total RNA Kit, and cDNA was synthesized with Thermo Scientific DyNAmo cDNA Synthesis Kit. Two samples failed during the RNA extraction and cDNA synthesis steps, leaving 38 samples in total.
Our partial genomic sequencing shows that there may be more than one FT gene copy in Boechera stricta (Joint Genome Institute and Mitchell-Olds lab, unpublished). Therefore, we cloned and sequenced FT full-length coding sequences from both parents. Only one copy is expressed, and both parents have the same expressing copy with identical coding region sequences (KJ576855 and KJ576856 in GenBank, where the Montana genotype is denoted as ‘LTM’ and Colorado genotype as ‘SAD12’). All primer sequences are available in Table S4. FT gene expression was measured by quantitative PCR (qPCR) with Thermo Scientific DyNAmo SYBR Green qPCR Kits. Following previous experiments [81], the ACTIN2 gene (ACT2) is used as reference gene, and FT expression level for each of the 38 samples was calculated as:
where CtACT2 is the Ct value in qPCR of the reference gene ACTIN2, and CtFT is the Ct value of FT. Since within each sample the Ct value of FT is always larger (i.e., the signal is lower) than ACT2, ΔCt is always negative, and larger ΔCt represents higher FT gene expression. The relative qPCR signal of FT to ACT2 can be calculated as 2ΔCt. This 2ΔCt value, however, has a skewed distribution among samples. Since log transformation of 2ΔCt yields a value that is proportional to ΔCt, we used the original ΔCt as the response variable for statistical analysis. Relevant data are available in Dataset S2.Statistical analysis was performed as in the HIF phenotypic experiment, where nFT genotype, HIF, and nFT by HIF interaction were treated as fixed effects, and family was treated as a random effect nested within nFT and HIF. All 40 plants were grown in the same block, so no block effect exists for this experiment. To further test if FT expression in Boechera stricta is related with flowering, we recorded whether each of the 40 experimental plants had visible flowering buds during the time of leaf-tissue collection. The analysis incorporates ΔCt as the response variable, and the phenological indicator ‘whether a plant has visible bud’ as a fixed-effect categorical predictor, and family as random-effect predictor variable.
Supporting Information
Zdroje
1. MackayTFC (2001) The Genetic Architecture Of Quantitative Traits. Annu Rev Genet 35 : 303–339.
2. KellyJK (2009) CONNECTING QTLS TO THE G-MATRIX OF EVOLUTIONARY QUANTITATIVE GENETICS. Evolution 63 : 813–825.
3. SteppanSJ, PhillipsPC, HouleD (2002) Comparative quantitative genetics: evolution of the G matrix. Trends Ecol Evol
4. ElenaSF, LenskiRE (2001) Epistasis between new mutations and genetic background and a test of genetic canalization. Evolution 55 : 1746–1752.
5. MeiklejohnCD, HartlDL (2002) A single mode of canalization. Trends Ecol Evol 17 : 468–473.
6. FlattT (2005) The evolutionary genetics of canalization. Q Rev Biol 80 : 287–316.
7. HallMC, DworkinI, UngererMC, PuruggananM (2007) Genetics of microenvironmental canalization in Arabidopsis thaliana. Proc Natl Acad Sci U S A 104 : 13717–13722.
8. ShenX, PetterssonM, RönnegårdL, CarlborgÖ (2012) Inheritance beyond plain heritability: variance-controlling genes in Arabidopsis thaliana. PLoS Genetics 8: e1002839.
9. Jimenez-GomezJM, CorwinJA, JosephB, MaloofJN, KliebensteinDJ (2011) Genomic analysis of QTLs and genes altering natural variation in stochastic noise. PLoS Genetics 7: e1002295.
10. AnselJ, BottinH, Rodriguez-BeltranC, DamonC, NagarajanM, et al. (2008) Cell-to-cell stochastic variation in gene expression is a complex genetic trait. PLoS Genetics 4: e1000049.
11. PerryGM, NehrkeKW, BushinskyDA, ReidR, LewandowskiKL, et al. (2012) Sex modifies genetic effects on residual variance in urinary calcium excretion in rat (Rattus norvegicus). Genetics 191 : 1003–1013.
12. FraserHB, SchadtEE (2010) The quantitative genetics of phenotypic robustness. PLoS One 5: e8635.
13. YangJ, LoosRJF, PowellJE, MedlandSE, SpeliotesEK, et al. (2012) FTO genotype is associated with phenotypic variability of body mass index. Nature 490 : 267–272.
14. HulseAM, CaiJJ (2013) Genetic variants contribute to gene expression variability in humans. Genetics 193 : 95–108.
15. PareG, CookNR, RidkerPM, ChasmanDI (2010) On the use of variance per genotype as a tool to identify quantitative trait interaction effects: a report from the Women's Genome Health Study. PLoS Genet 6: e1000981.
16. WangG, YangE, Brinkmeyer-LangfordCL, CaiJJ (2014) Additive, Epistatic, and Environmental Effects Through the Lens of Expression Variability QTL in a Twin Cohort. Genetics 196 : 413–425.
17. WagnerGP, BoothG, Bagheri-ChaichianH (1997) A population genetic theory of canalization. Evolution 329–347.
18. GibsonG, WagnerG (2000) Canalization in evolutionary genetics: a stabilizing theory? BioEssays 22 : 372–380.
19. LandeR (1979) Quantitative genetic analysis of multivariate evolution, applied to brain: body size allometry. Evolution 33 : 402–416.
20. De JongG (1995) Phenotypic plasticity as a product of selection in a variable environment. Am Nat 493–512.
21. FalconerDS (1952) The problem of environment and selection. Am Nat 293–298.
22. YamadaY (1962) Genotype by environment interaction and genetic correlation of the same trait under different environments. Jpn J Genet 37 : 498–509.
23. ArnoldSJ (1992) Constraints on phenotypic evolution. Am Nat S85–S107.
24. ForrestJ, Miller-RushingAJ (2010) Toward a synthetic understanding of the role of phenology in ecology and evolution. Philos Trans R Soc Lond B Biol Sci 365 : 3101–3112.
25. AndersonJT, LeeC-R, Mitchell-OldsT (2011) Life history QTLs and natural selection on flowering time in Boechera stricta, a perennial relative of Arabidopsis. Evolution 65 : 771–787.
26. RushworthCA, SongB-H, LeeC-R, Mitchell-OldsT (2011) Boechera, a model system for ecological genomics. Mol Ecol 20 : 4843–4857.
27. AndersonJT, LeeC-R, Mitchell-OldsT (2014) Strong selection genome-wide enhances fitness trade-offs across environments and episodes of selection. Evolution 68 : 16–31.
28. AndersonJT, LeeC-R, RushworthC, ColauttiRI, Mitchell-OldsT (2012) Genetic tradeoffs and conditional neutrality contribute to local adaptation. Mol Ecol 22 : 699–708.
29. RutherfordSL, LindquistS (1998) Hsp90 as a capacitor for morphological evolution. Nature 396 : 336–342.
30. PinPA, NilssonO (2012) The multifaceted roles of FLOWERING LOCUS T in plant development. Plant Cell Environ 35 : 1742–1755.
31. BoxGEP (1949) A general distribution theory for a class of likelihood criteria. Biometrika 317–346.
32. BlowsMW, ChenowethSF, HineE (2004) Orientation of the genetic variance-covariance matrix and the fitness surface for multiple male sexually selected traits. Am Nat 163 : 329–340.
33. KrzanowskiWJ (1979) Between-groups comparison of principal components. Journal of the American Statistical Association 74 : 703–707.
34. HuangW, RichardsS, CarboneMA, ZhuD, AnholtRRH, et al. (2012) Epistasis dominates the genetic architecture of Drosophila quantitative traits. Proc Natl Acad Sci 109 : 15553–15559.
35. BreenMS, KemenaC, VlasovPK, NotredameC, KondrashovFA (2012) Epistasis as the primary factor in molecular evolution. Nature 490 : 535–538.
36. KellyJK (2005) Epistasis in monkeyflowers. Genetics 171 : 1917–1931.
37. CaicedoAL, StinchcombeJR, OlsenKM, SchmittJ, PuruggananMD (2004) Epistatic interaction between Arabidopsis FRI and FLC flowering time genes generates a latitudinal cline in a life history trait. Proc Natl Acad Sci 101 : 15670–15675.
38. CarlborgO, JacobssonL, AhgrenP, SiegelP, AnderssonL (2006) Epistasis and the release of genetic variation during long-term selection. Nat Genet 38 : 418–420.
39. CarlborgO, HaleyCS (2004) Epistasis: too often neglected in complex trait studies? Nat Rev Genet 5 : 618-U614.
40. CamargoL, OsbornT (1996) Mapping loci controlling flowering time in Brassica oleracea. Theor Appl Genet 92 : 610–616.
41. SimpsonGG, DeanC (2002) Arabidopsis, the Rosetta stone of flowering time? Science 296 : 285–289.
42. WelchSM, RoeJL, DongZ (2003) A Genetic Neural Network Model of Flowering Time Control in Arabidopsis thaliana. Agron J 95 : 71–81.
43. PaabyAB, RockmanMV (2014) Cryptic genetic variation: evolution's hidden substrate. Nat Rev Genet 247–58.
44. RohnerN, JaroszDF, KowalkoJE, YoshizawaM, JefferyWR, et al. (2013) Cryptic variation in morphological evolution: HSP90 as a capacitor for loss of eyes in cavefish. Science 342 : 1372–1375.
45. SchlesingerMJ (1990) Heat shock proteins. J Biol Chem 265 : 12111–12114.
46. WiechH, BuchnerJ, ZimmermannR, JakobU (1992) Hsp90 chaperones protein folding in vitro. Nature 358 : 169–170.
47. Gething M-J, Sambrook J (1992) Protein folding in the cell.
48. SiegalML, BergmanA (2002) Waddington's canalization revisited: Developmental stability and evolution. PNAS 99 : 10528–14660.
49. BergmanA, SiegalML (2003) Evolutionary capacitance as a general feature of complex gene networks. Nature 424 : 549–552.
50. LevySF, SiegalML (2008) Network hubs buffer environmental variation in Saccharomyces cerevisiae. PLoS Biol 6: e264.
51. FinlayKW, WilkinsonGN (1963) The analysis of adaptation in a plant-breeding programme. Aust J Agric Res 14 : 742–754.
52. StinchcombeJR, WeinigC, UngererM, OlsenKM, MaysC, et al. (2004) A latitudinal cline in flowering time in Arabidopsis thaliana modulated by the flowering time gene FRIGIDA. Proc Natl Acad Sci 101 : 4712–4717.
53. ProulxSR, PhillipsPC (2005) The opportunity for canalization and the evolution of genetic networks. Am Nat 165 : 147–162.
54. PetterssonME, NelsonRM, CarlborgÖ (2012) Selection On Variance-Controlling Genes: Adaptability or Stability. Evolution 66 : 3945–3949.
55. StearnsSC, KaweckiTJ (1994) Fitness sensitivity and the canalization of life-history traits. Evolution 1438–1450.
56. StearnsSC, KaiserM, KaweckiTJ (1995) The differential genetic and environmental canalization of fitness components in Drosophila melanogaster. J Evol Biol 8 : 539–557.
57. WadeMJ (2001) Epistasis, complex traits, and mapping genes. Genetica 112–113 : 59–69.
58. ArnoldSJ, BürgerR, HohenlohePA, AjieBC, JonesAG (2008) Understanding the evolution and stability of the G-matrix. Evolution 62 : 2451–2461.
59. StinchcombeJR, SimonsenAK, BlowsM (2013) ESTIMATING UNCERTAINTY IN MULTIVARIATE RESPONSES TO SELECTION. Evolution 68 : 1188–1196.
60. AguirreJD, HineE, McGuiganK, BlowsMW (2014) Comparing G: multivariate analysis of genetic variation in multiple populations. Heredity 112 : 21–29.
61. StinchcombeJR, WeinigC, HeathKD, BrockMT, SchmittJ (2009) Polymorphic Genes of Major Effect: Consequences for Variation, Selection and Evolution in Arabidopsis thaliana. Genetics 182 : 911–922.
62. WolfJB, LeamyLJ, RoutmanEJ, CheverudJM (2005) Epistatic pleiotropy and the genetic architecture of covariation within early and late-developing skull trait complexes in mice. Genetics 171 : 683–694.
63. DebatV, DavidP (2001) Mapping phenotypes: canalization, plasticity and developmental stability. Trends Ecol Evol 16 : 555–561.
64. SgroCM, HoffmannAA (2004) Genetic correlations, tradeoffs and environmental variation. Heredity 93 : 241–248.
65. Mendez-VigoB, Martinez-ZapaterJM, Alonso-BlancoC (2013) The flowering repressor SVP underlies a novel Arabidopsis thaliana QTL interacting with the genetic background. PLoS Genet 9: e1003289.
66. KorvesTM, SchmidKJ, CaicedoAL, MaysC, StinchcombeJR, et al. (2007) Fitness effects associated with the major flowering time gene FRIGIDA in Arabidopsis thaliana in the field. Am Nat 169: E141–E157.
67. BrownAA, BuilA, ViñuelaA, LappalainenT, ZhengH-F, et al. (2014) Genetic interactions affecting human gene expression identified by variance association mapping. eLife 3.
68. BeavisWD (1994) The power and deceit of QTL experiments: Lessons from comparative QTL studies. Proceedings of the forty-ninth annual corn and sorghum industry research conference 49 : 250–266.
69. Beavis WD (1998) QTL analyses: power, precision, and accuracy. In: Paterson AH, editor. Molecular dissection of complex traits. Boca Raton: CRC Press. pp. 145–162.
70. XuSZ (2003) Theoretical basis of the Beavis effect. Genetics 165 : 2259–2268.
71. TonsorSJ, ElnaccashTW, ScheinerSM (2013) Developmental instability is genetically correlated with phenotypic plasticity, constraining heritability, and fitness. Evolution 67 : 2923–2935.
72. SchranzME, ManzanedaAJ, WindsorAJ, ClaussMJ, Mitchell-OldsT (2009) Ecological genomics of Boechera stricta: identification of a QTL controlling the allocation of methionine - vs branched-chain amino acid-derived glucosinolates and levels of insect herbivory. Heredity 102 : 465–474.
73. ChurchillGA, DoergeRW (1994) Empirical threshold values for quantitative trait mapping. Genetics 138 : 963–971.
74. ValladaresF, Sanchez-GomezD, ZavalaMA (2006) Quantitative estimation of phenotypic plasticity: bridging the gap between the evolutionary concept and its ecological applications. J Ecol 94 : 1103–1116.
75. SchluterD (1996) Adaptive radiation along genetic lines of least resistance. Evolution 50 : 1766–1774.
76. LeeC-R, Mitchell-OldsT (2013) Complex trait divergence contributes to environmental niche differentiation in ecological speciation of Boechera stricta. Mol Ecol 22 : 2204–2217.
77. CorbesierL, VincentC, JangS, FornaraF, FanQ, et al. (2007) FT Protein Movement Contributes to Long-Distance Signaling in Floral Induction of Arabidopsis. Science 316 : 1030–1033.
78. KimSY, YuX, MichaelsSD (2008) Regulation of CONSTANS and FLOWERING LOCUS T Expression in Response to Changing Light Quality. Plant Physiol 148 : 269–279.
79. ChengXF, WangZY (2005) Overexpression of COL9, a CONSTANS-LIKE gene, delays flowering by reducing expression of CO and FT in Arabidopsis thaliana. Plant J 43 : 758–768.
80. YanovskyMJ, KaySA (2002) Molecular basis of seasonal time measurement in Arabidopsis. Nature 419 : 308–312.
81. PrasadKVSK, SongBH, Olson-ManningC, AndersonJT, LeeCR, et al. (2012) A gain-of-function polymorphism controlling complex traits and fitness in nature. Science 337 : 1081–1084.
Štítky
Genetika Reprodukční medicína
Článek Oligoasthenoteratozoospermia and Infertility in Mice Deficient for miR-34b/c and miR-449 LociČlánek The Kinesin AtPSS1 Promotes Synapsis and is Required for Proper Crossover Distribution in MeiosisČlánek Payoffs, Not Tradeoffs, in the Adaptation of a Virus to Ostensibly Conflicting Selective PressuresČlánek Examination of Prokaryotic Multipartite Genome Evolution through Experimental Genome ReductionČlánek BMP-FGF Signaling Axis Mediates Wnt-Induced Epidermal Stratification in Developing Mammalian SkinČlánek Role of STN1 and DNA Polymerase α in Telomere Stability and Genome-Wide Replication in ArabidopsisČlánek RNA-Processing Protein TDP-43 Regulates FOXO-Dependent Protein Quality Control in Stress ResponseČlánek Integrating Functional Data to Prioritize Causal Variants in Statistical Fine-Mapping StudiesČlánek Salt-Induced Stabilization of EIN3/EIL1 Confers Salinity Tolerance by Deterring ROS Accumulation inČlánek Ethylene-Induced Inhibition of Root Growth Requires Abscisic Acid Function in Rice ( L.) SeedlingsČlánek Metabolic Respiration Induces AMPK- and Ire1p-Dependent Activation of the p38-Type HOG MAPK PathwayČlánek Signature Gene Expression Reveals Novel Clues to the Molecular Mechanisms of Dimorphic Transition inČlánek A Mouse Model Uncovers LKB1 as an UVB-Induced DNA Damage Sensor Mediating CDKN1A (p21) DegradationČlánek Dominant Sequences of Human Major Histocompatibility Complex Conserved Extended Haplotypes from to
Článek vyšel v časopisePLOS Genetics
Nejčtenější tento týden
2014 Číslo 10- IVF a rakovina prsu – zvyšují hormony riziko vzniku rakoviny?
- Akutní intermitentní porfyrie
- Souvislost haplotypu M2 genu pro annexin A5 s opakovanými reprodukčními ztrátami
- Transthyretinová amyloidóza z pohledu neurologa a kardiologa aneb jak se vyhnout „misdiagnostice“?
- Hypogonadotropní hypogonadismus u žen a vliv na výsledky reprodukce po IVF
-
Všechny články tohoto čísla
- An Deletion Is Highly Associated with a Juvenile-Onset Inherited Polyneuropathy in Leonberger and Saint Bernard Dogs
- Licensing of Yeast Centrosome Duplication Requires Phosphoregulation of Sfi1
- Oligoasthenoteratozoospermia and Infertility in Mice Deficient for miR-34b/c and miR-449 Loci
- Basement Membrane and Cell Integrity of Self-Tissues in Maintaining Immunological Tolerance
- The Kinesin AtPSS1 Promotes Synapsis and is Required for Proper Crossover Distribution in Meiosis
- Germline Mutations in Are Associated with Familial Gastric Cancer
- POT1a and Components of CST Engage Telomerase and Regulate Its Activity in
- Controlling Meiotic Recombinational Repair – Specifying the Roles of ZMMs, Sgs1 and Mus81/Mms4 in Crossover Formation
- Payoffs, Not Tradeoffs, in the Adaptation of a Virus to Ostensibly Conflicting Selective Pressures
- FHIT Suppresses Epithelial-Mesenchymal Transition (EMT) and Metastasis in Lung Cancer through Modulation of MicroRNAs
- Genome-Wide Mapping of Yeast RNA Polymerase II Termination
- Examination of Prokaryotic Multipartite Genome Evolution through Experimental Genome Reduction
- White Cells Facilitate Opposite- and Same-Sex Mating of Opaque Cells in
- BMP-FGF Signaling Axis Mediates Wnt-Induced Epidermal Stratification in Developing Mammalian Skin
- Genome-Wide Association Study of CSF Levels of 59 Alzheimer's Disease Candidate Proteins: Significant Associations with Proteins Involved in Amyloid Processing and Inflammation
- COE Loss-of-Function Analysis Reveals a Genetic Program Underlying Maintenance and Regeneration of the Nervous System in Planarians
- Fat-Dachsous Signaling Coordinates Cartilage Differentiation and Polarity during Craniofacial Development
- Identification of Genes Important for Cutaneous Function Revealed by a Large Scale Reverse Genetic Screen in the Mouse
- Sensors at Centrosomes Reveal Determinants of Local Separase Activity
- Genes Integrate and Hedgehog Pathways in the Second Heart Field for Cardiac Septation
- Systematic Dissection of Coding Exons at Single Nucleotide Resolution Supports an Additional Role in Cell-Specific Transcriptional Regulation
- Recovery from an Acute Infection in Requires the GATA Transcription Factor ELT-2
- HIPPO Pathway Members Restrict SOX2 to the Inner Cell Mass Where It Promotes ICM Fates in the Mouse Blastocyst
- Role of and in Development of Abdominal Epithelia Breaks Posterior Prevalence Rule
- The Formation of Endoderm-Derived Taste Sensory Organs Requires a -Dependent Expansion of Embryonic Taste Bud Progenitor Cells
- Role of STN1 and DNA Polymerase α in Telomere Stability and Genome-Wide Replication in Arabidopsis
- Keratin 76 Is Required for Tight Junction Function and Maintenance of the Skin Barrier
- Encodes the Catalytic Subunit of N Alpha-Acetyltransferase that Regulates Development, Metabolism and Adult Lifespan
- Disruption of SUMO-Specific Protease 2 Induces Mitochondria Mediated Neurodegeneration
- Caudal Regulates the Spatiotemporal Dynamics of Pair-Rule Waves in
- It's All in Your Mind: Determining Germ Cell Fate by Neuronal IRE-1 in
- A Conserved Role for Homologs in Protecting Dopaminergic Neurons from Oxidative Stress
- The Master Activator of IncA/C Conjugative Plasmids Stimulates Genomic Islands and Multidrug Resistance Dissemination
- An AGEF-1/Arf GTPase/AP-1 Ensemble Antagonizes LET-23 EGFR Basolateral Localization and Signaling during Vulva Induction
- The Proteomic Landscape of the Suprachiasmatic Nucleus Clock Reveals Large-Scale Coordination of Key Biological Processes
- RNA-Processing Protein TDP-43 Regulates FOXO-Dependent Protein Quality Control in Stress Response
- A Complex Genetic Switch Involving Overlapping Divergent Promoters and DNA Looping Regulates Expression of Conjugation Genes of a Gram-positive Plasmid
- ZTF-8 Interacts with the 9-1-1 Complex and Is Required for DNA Damage Response and Double-Strand Break Repair in the Germline
- Integrating Functional Data to Prioritize Causal Variants in Statistical Fine-Mapping Studies
- Tpz1-Ccq1 and Tpz1-Poz1 Interactions within Fission Yeast Shelterin Modulate Ccq1 Thr93 Phosphorylation and Telomerase Recruitment
- Salt-Induced Stabilization of EIN3/EIL1 Confers Salinity Tolerance by Deterring ROS Accumulation in
- Telomeric (s) in spp. Encode Mediator Subunits That Regulate Distinct Virulence Traits
- Ethylene-Induced Inhibition of Root Growth Requires Abscisic Acid Function in Rice ( L.) Seedlings
- Ancient Expansion of the Hox Cluster in Lepidoptera Generated Four Homeobox Genes Implicated in Extra-Embryonic Tissue Formation
- Mechanism of Suppression of Chromosomal Instability by DNA Polymerase POLQ
- A Mutation in the Mouse Gene Leads to Impaired Hedgehog Signaling
- Keeping mtDNA in Shape between Generations
- Targeted Exon Capture and Sequencing in Sporadic Amyotrophic Lateral Sclerosis
- TIF-IA-Dependent Regulation of Ribosome Synthesis in Muscle Is Required to Maintain Systemic Insulin Signaling and Larval Growth
- At Short Telomeres Tel1 Directs Early Replication and Phosphorylates Rif1
- Evidence of a Bacterial Receptor for Lysozyme: Binding of Lysozyme to the Anti-σ Factor RsiV Controls Activation of the ECF σ Factor σ
- Hsp40s Specify Functions of Hsp104 and Hsp90 Protein Chaperone Machines
- Feeding State, Insulin and NPR-1 Modulate Chemoreceptor Gene Expression via Integration of Sensory and Circuit Inputs
- Functional Interaction between Ribosomal Protein L6 and RbgA during Ribosome Assembly
- Multiple Regulatory Systems Coordinate DNA Replication with Cell Growth in
- Fast Evolution from Precast Bricks: Genomics of Young Freshwater Populations of Threespine Stickleback
- Mmp1 Processing of the PDF Neuropeptide Regulates Circadian Structural Plasticity of Pacemaker Neurons
- The Nuclear Immune Receptor Is Required for -Dependent Constitutive Defense Activation in
- Genetic Modifiers of Neurofibromatosis Type 1-Associated Café-au-Lait Macule Count Identified Using Multi-platform Analysis
- Juvenile Hormone-Receptor Complex Acts on and to Promote Polyploidy and Vitellogenesis in the Migratory Locust
- Uncovering Enhancer Functions Using the α-Globin Locus
- The Analysis of Mutant Alleles of Different Strength Reveals Multiple Functions of Topoisomerase 2 in Regulation of Chromosome Structure
- Metabolic Respiration Induces AMPK- and Ire1p-Dependent Activation of the p38-Type HOG MAPK Pathway
- The Specification and Global Reprogramming of Histone Epigenetic Marks during Gamete Formation and Early Embryo Development in
- The DAF-16 FOXO Transcription Factor Regulates to Modulate Stress Resistance in , Linking Insulin/IGF-1 Signaling to Protein N-Terminal Acetylation
- Genetic Influences on Translation in Yeast
- Analysis of Mutants Defective in the Cdk8 Module of Mediator Reveal Links between Metabolism and Biofilm Formation
- Ribosomal Readthrough at a Short UGA Stop Codon Context Triggers Dual Localization of Metabolic Enzymes in Fungi and Animals
- Gene Duplication Restores the Viability of Δ and Δ Mutants
- Selection on a Variant Associated with Improved Viral Clearance Drives Local, Adaptive Pseudogenization of Interferon Lambda 4 ()
- Break-Induced Replication Requires DNA Damage-Induced Phosphorylation of Pif1 and Leads to Telomere Lengthening
- Dynamic Partnership between TFIIH, PGC-1α and SIRT1 Is Impaired in Trichothiodystrophy
- Signature Gene Expression Reveals Novel Clues to the Molecular Mechanisms of Dimorphic Transition in
- Mutations in Moderate or Severe Intellectual Disability
- Multifaceted Genome Control by Set1 Dependent and Independent of H3K4 Methylation and the Set1C/COMPASS Complex
- A Role for Taiman in Insect Metamorphosis
- The Small RNA Rli27 Regulates a Cell Wall Protein inside Eukaryotic Cells by Targeting a Long 5′-UTR Variant
- MMS Exposure Promotes Increased MtDNA Mutagenesis in the Presence of Replication-Defective Disease-Associated DNA Polymerase γ Variants
- Coexistence and Within-Host Evolution of Diversified Lineages of Hypermutable in Long-term Cystic Fibrosis Infections
- Comprehensive Mapping of the Flagellar Regulatory Network
- Topoisomerase II Is Required for the Proper Separation of Heterochromatic Regions during Female Meiosis
- A Splice Mutation in the Gene Causes High Glycogen Content and Low Meat Quality in Pig Skeletal Muscle
- KDM5 Interacts with Foxo to Modulate Cellular Levels of Oxidative Stress
- H2B Mono-ubiquitylation Facilitates Fork Stalling and Recovery during Replication Stress by Coordinating Rad53 Activation and Chromatin Assembly
- Copy Number Variation in the Horse Genome
- Unifying Genetic Canalization, Genetic Constraint, and Genotype-by-Environment Interaction: QTL by Genomic Background by Environment Interaction of Flowering Time in
- Spinster Homolog 2 () Deficiency Causes Early Onset Progressive Hearing Loss
- Genome-Wide Discovery of Drug-Dependent Human Liver Regulatory Elements
- Developmentally-Regulated Excision of the SPβ Prophage Reconstitutes a Gene Required for Spore Envelope Maturation in
- Protein Phosphatase 4 Promotes Chromosome Pairing and Synapsis, and Contributes to Maintaining Crossover Competence with Increasing Age
- The bHLH-PAS Transcription Factor Dysfusion Regulates Tarsal Joint Formation in Response to Notch Activity during Leg Development
- A Mouse Model Uncovers LKB1 as an UVB-Induced DNA Damage Sensor Mediating CDKN1A (p21) Degradation
- Notch3 Interactome Analysis Identified WWP2 as a Negative Regulator of Notch3 Signaling in Ovarian Cancer
- An Integrated Cell Purification and Genomics Strategy Reveals Multiple Regulators of Pancreas Development
- Dominant Sequences of Human Major Histocompatibility Complex Conserved Extended Haplotypes from to
- The Vesicle Protein SAM-4 Regulates the Processivity of Synaptic Vesicle Transport
- A Gain-of-Function Mutation in Impeded Bone Development through Increasing Expression in DA2B Mice
- Nephronophthisis-Associated Regulates Cell Cycle Progression, Apoptosis and Epithelial-to-Mesenchymal Transition
- Beclin 1 Is Required for Neuron Viability and Regulates Endosome Pathways via the UVRAG-VPS34 Complex
- The Not5 Subunit of the Ccr4-Not Complex Connects Transcription and Translation
- Abnormal Dosage of Ultraconserved Elements Is Highly Disfavored in Healthy Cells but Not Cancer Cells
- Genome-Wide Distribution of RNA-DNA Hybrids Identifies RNase H Targets in tRNA Genes, Retrotransposons and Mitochondria
- The Chromosomal Association of the Smc5/6 Complex Depends on Cohesion and Predicts the Level of Sister Chromatid Entanglement
- Cell-Autonomous Progeroid Changes in Conditional Mouse Models for Repair Endonuclease XPG Deficiency
- PLOS Genetics
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- The Master Activator of IncA/C Conjugative Plasmids Stimulates Genomic Islands and Multidrug Resistance Dissemination
- A Splice Mutation in the Gene Causes High Glycogen Content and Low Meat Quality in Pig Skeletal Muscle
- Keratin 76 Is Required for Tight Junction Function and Maintenance of the Skin Barrier
- A Role for Taiman in Insect Metamorphosis
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání











