-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaAnalýza dat v neurologii
XXVIII. Hodnocení diagnostických testů – křivky ROC
Autoři: L. Dušek; T. Pavlík; Jiří Jarkovský
; J. Koptíková
Působiště autorů: Institut biostatistiky a analýz, Masarykova univerzita, Brno
Vyšlo v časopise: Cesk Slov Neurol N 2011; 74/107(4): 493-499
Kategorie: Okénko statistika
V předcházejících dílech seriálu jsme rozebrali různé aspekty hodnocení diagnostických testů s binárními výstupy typu 1/0 nebo pozitivní/negativní. Odvodili jsme řadu ukazatelů diagnostické síly testů, v první řadě senzitivitu, specificitu, prediktivní hodnotu a věrohodnostní poměr. Žádný z těchto parametrů ale nemůžeme přímočaře využít u testů, jejichž výstupem je spojitá (kvantitativní) proměnná, např. koncentrace analytu v krevním séru nebo systolický krevní tlak. Je-li kvantitativní test využíván v diagnostice dostatečně dlouho, má již vybudovanou škálu odlišující normální a patologické hodnoty. Na základě předchozích výzkumů tedy známe dělicí body, podle kterých můžeme spojitou hodnotu tzv. dichotomizovat, a dospět tak k výstupu typu pozitivní/negativní. Pokud ale v této fázi poznání nejsme, musíme pracovat přímo se spojitou proměnnou, přičemž cíl analýzy opět směřuje k objektivnímu posouzení diagnostické síly a věrohodnosti testu. Novým cílem je snaha nalézt vhodné dělicí body, kterými lze spojitou škálu kategorizovat, a usnadnit tak diagnostická rozhodnutí. Obdobný problém řešíme i v případě, kdy na výstupu testu stojí ordinální proměnná, neboť i ta nabývá více vzájemně odstupňovaných hodnot, a hledání diagnosticky využitelných dělicích bodů je na místě.
Práce se spojitými výsledky testů se v principech neliší od zpracování výstupů binárních. Opět na základě testu usuzujeme na přítomnost nemoci u hodnoceného jedince. A opět se můžeme rozhodnout správně i nesprávně, což znamená, že se dopustíme falešně pozitivního nebo falešně negativního závěru. Obr. 1a ukazuje modelovou situaci, kdy dle hodnot spojité proměnné X odlišujeme zdravé a nemocné jedince. Vidíme, že ačkoli se obě skupiny v hodnotách proměnné X liší, rozdělení obou skupin se částečně překrývají, a v hraničních hodnotách se tedy můžeme dopustit chyby. Cílem naší analýzy je:
- a) určit, zda je proměnná X vhodná pro diagnostické odlišování zdravých a nemocných jedinců; tedy zda pravděpodobnost chybných rozhodnutí nepřesahuje únosnou mez;
- b) stanovit dělicí bod na škále hodnot X (někdy také nazývaný prahový bod, hodnota prahu, hraniční hodnota, angl. „cut-off point“), abychom dosáhli diagnosticky přijatelné pravděpodobnosti falešně negativních a falešně pozitivních výsledků.
Tento postup s využitím tří různých dělicích bodů znázorňuje obrázek 1c–e. Obr. 1b představuje tzv. křivku ROC (Receiver Operating Characteristic), která je standardním nástrojem pro grafickou vizualizaci výstupů diagnostických testů. Konstrukce křivky využívá faktu, že jakákoli hodnota spojité proměněné X (označujeme xi, kde i = 1,…n) nějak rozlišuje zdravé a nemocné jedince (obr. 1), a tedy každá hodnota xi je spojena s nějakou specificitou a senzitivitou. Křivku ROC získáme spojením bodů určených senzitivitou a hodnotou (1 – specificita), které přísluší jednotlivým hodnotám proměnné X. ROC křivku lze také zakreslit jako spojnici bodů určených podílem správně pozitivních rozhodnutí mezi všemi pozitivními (vertikální osa) a podílem falešně pozitivních mezi všemi pozitivními rozhodnutími (horizontální osa), opět náležejících jednotlivým hodnotám proměnné X jako výstupu testu. Tento alternativní způsob vyjádření je v literatuře nazýván Relative Operating Characteristic Curve.
Obr. 1. Prezentace významu analýz ROC. 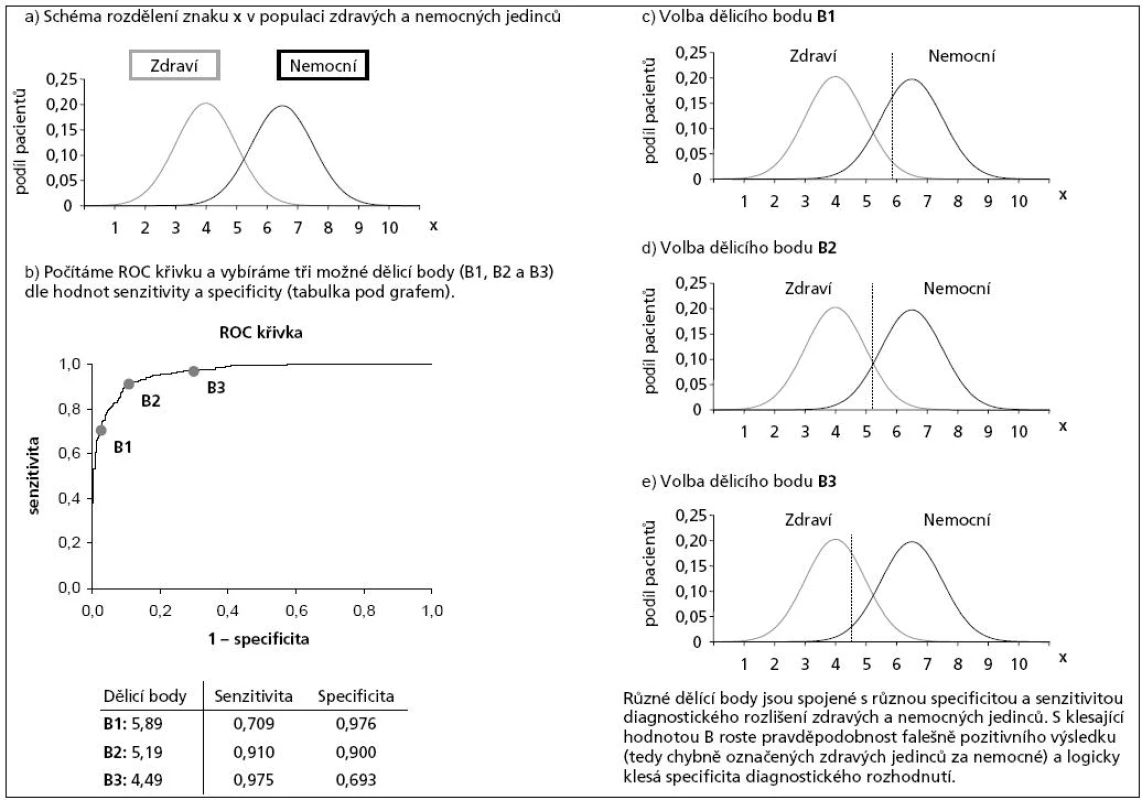
Ovšem ne každý výstup testu dobře rozlišuje sledované skupiny jedinců. Nadto i v případě dobrého rozlišení pouze některé hodnoty X nabízejí diagnosticky využitelné rozlišení skupin. Smyslem analýzy ROC je usnadnit výběr vhodných dělicích bodů. Opět využijme příkladu na obr. 1. Nízké hodnoty proměnné X (např. hodnoty < 2) nejsou dobrým dělicím kritériem, neboť všichni nemocní i převážná část zdravých jedinců nabývají hodnot větších. Tzn. hodnoty X menší než 2 znamenají sice 100% identifikaci zdravého jedince, ale hodnoty vyšší mají velmi slabý diagnostický potenciál. A obdobně např. hodnoty X > 8 se 100% pravděpodobností identifikují nemocného člověka, ale nižší hodnoty nepřispívají k rozlišení skupin. Extrémní hodnoty kvantitativních výstupů testu maximalizují buď specificitu, nebo senzitivitu, přičemž ale druhý z těchto ukazatelů nabývá minimálních až nulových hodnot. Takové hodnoty nejsou diagnosticky spolehlivé hraniční hodnoty. Diagnosticky nejlépe využitelné dělicí body nabízejí maximální součet hodnot senzitivity a specificity a vybalancovávají tak pravděpodobnost falešně pozitivních a falešně negativních závěrů. Tyto body většinou najdeme ve střední části křivky ROC (např. bod B2 na obr. 1). Význam volby dělicích bodů u spojité proměnné dále přibližuje obr. 2.
Obr. 2. Volba hraničních hodnot (dělicích bodů) pro označení/neoznačení jedince jako pacienta dle hodnot diagnostického testu. 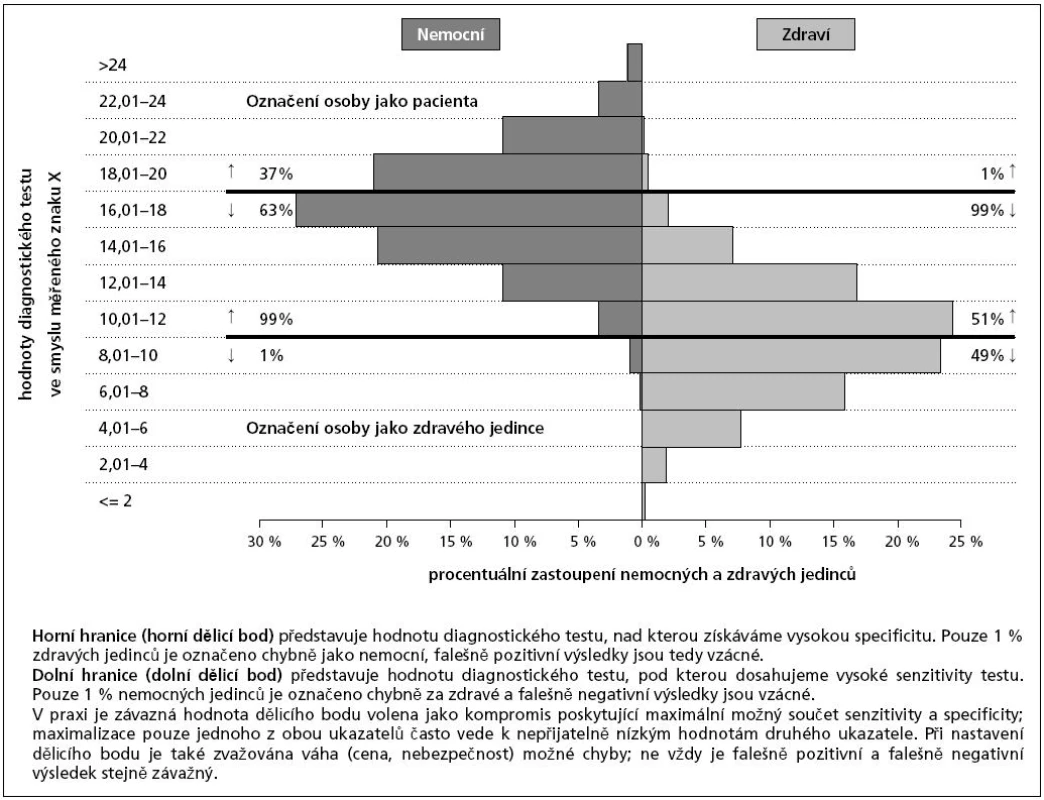
ROC analýza není omezena pouze na spojité (kvantitativní) výstupy testů, lze ji sestrojit i pro výstupy ordinální. ROC křivka z definice vyhodnocuje všechny možné dělicí body dané hodnotami získanými na výstupu diagnostického testu. Jakýkoli možný výsledek testu je dělicím bodem, protože pro něj lze zjistit senzitivitu a specificitu v odlišení skupiny zdravých a nemocných jedinců. Na grafu ROC křivky tyto body buď přímo vidíme (leží na samotné křivce – obr. 1b),anebo vykresleny nejsou. Logicky je pak křivka ROC generovaná z malého počtu hodnot ordinální proměnné méně vyhlazená, stupňovitá. Ukázka analýzy ROC pro ordinální znak včetně optimální volby dělicího bodu je uvedena v příkladu 1.
Další často využívanou přidanou hodnotou křivek ROC je fakt, že umožňují porovnat diagnostickou sílu různých testů, a to i s různou proměnnou na výstupu. Lze totiž vykreslit křivky ROC spojující pravděpodobnostní hodnoty specificity a senzitivity pro všechny možné hodnoty různých spojitých nebo ordinální proměnných. Můžeme tak v jednom grafu jednoduše porovnat diagnostickou sílu i velmi rozdílných testů. Příklady takových srovnání přinášejí obr. 3 a 4.
Obr. 3. Ukázky využití křivek ROC pro srovnání tří diagnostických testů (metod). 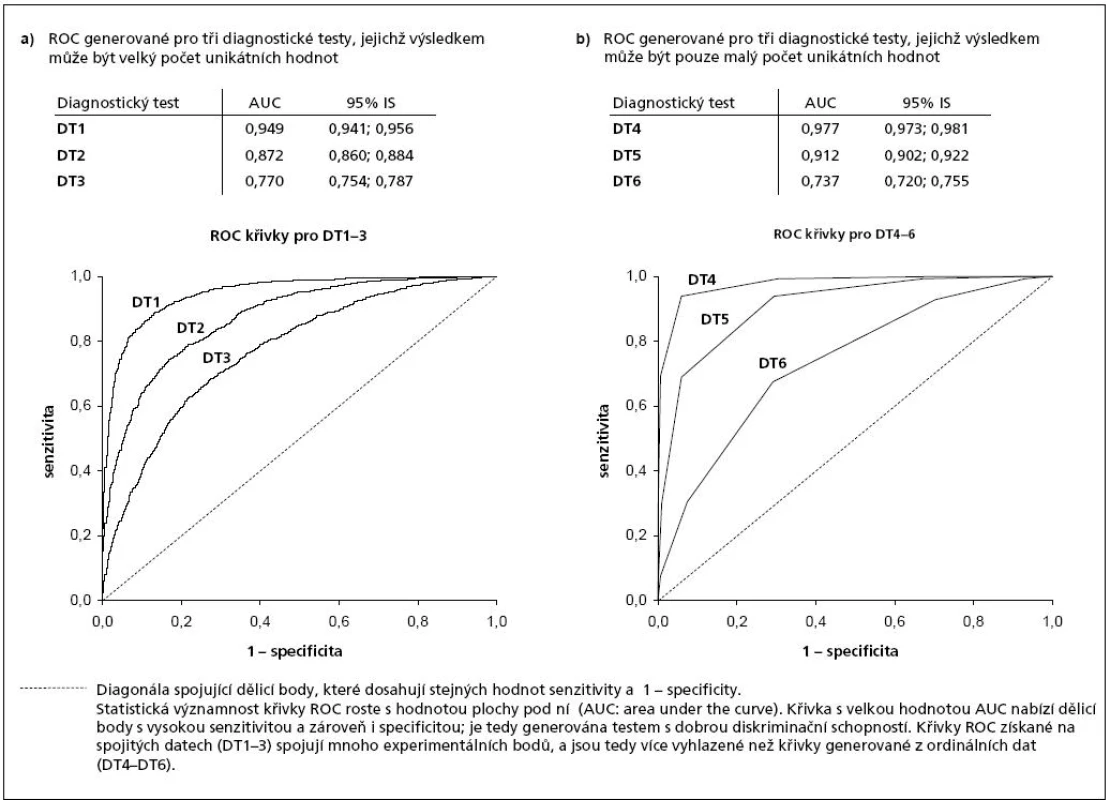
Obr. 4. Ukázka výstupů analýzy ROC dvou znaků, X1 a X2, diagnosticky odlišujících pacienty s a bez komplikací. 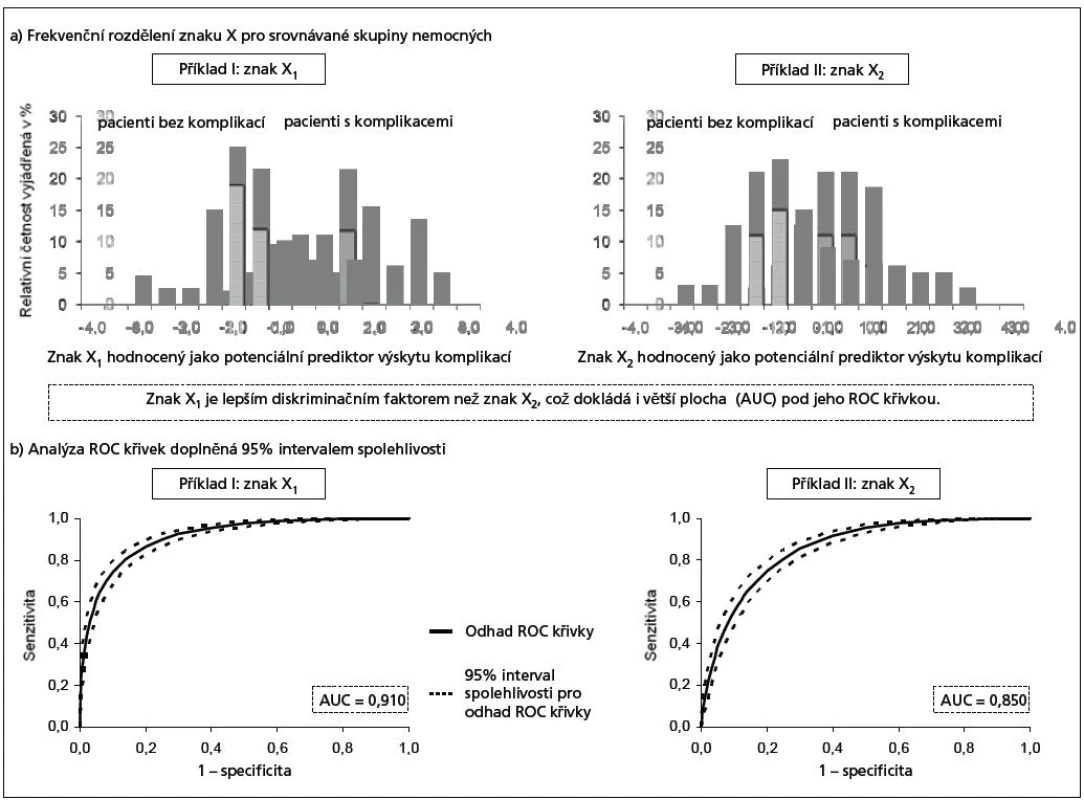
U testu, který nemá žádnou schopnost diskriminovat stav nemoci a zdraví, probíhá křivka ROC jako diagonála spojující body stejné numerické hodnoty (viz tečkovaná diagonála u křivek ROC na obr. 3). Body ležící na diagonále odpovídají výstupům testu, jehož diskriminační schopnost je rovna náhodnému tipování mezi zdravými a nemocnými jedinci. Obdobně také výstup testu, který generuje křivku ROC blízkou diagonále grafu, nenabízí v žádném bodě dostatečně vysokou senzitivitu a specificitu, a je tudíž diagnosticky nevyužitelný. Naopak nejlepší diagnostický potenciál náleží bodům ležícím v levé horní části ROC grafu, neboť vyjadřují výstup testu s vysokou senzitivitou i specificitou. Křivky ROC, které takové body zahrnují, jsou velmi vzdálené od diagonály, např. křivka pro test DT1 a DT4 na obr. 3.
Plocha grafu ROC (někdy nazývána ROC prostor) je vždy rovna 1, neboť senzitivita i (1 – specificita) mohou nabývat pouze hodnot od 0 do 1. Test s vysokou diagnostickou silou tedy poznáme podle křivek ROC, které obepínají co největší plochu grafu. Plocha pod ROC křivkou (AUC, Area Under the Curve) nabývá také hodnot 0 až 1 a slouží jako standardní vyjádření diagnostické efektivity testu. Je jasné, že výstup testu, který nerozlišuje mezi nemocnými a zdravými jedinci, nabídne ROC křivku s malou plochou. Následně nelze najít optimální dělicí body, neboť křivka nedosahuje uspokojivé hodnoty senzitivity a specificity (např. test DT6 na obr. 3). Jednou z možných interpretací hodnoty AUC je, že je rovna pravděpodobnosti, že náhodně vybraný jedinec ze skupiny negativních (zdravých) dopadl v testu lépe (nebo s nižší hodnotou), než náhodně vybraný jedinec z třídy pozitivních (nemocných).
Body a křivky ROC, které leží v ROC prostoru nad diagonálou, směřují k dobrému rozlišení zdravých a nemocných jedinců a naopak prostor pod diagonálou odráží špatnou klasifikaci. Body a křivky pod diagonálou mohou být ale zrcadlově překlopeny do oblasti nad diagonálou. Křivky ROC s plochou < 0,5 totiž popisují situaci, kdy na výstupu testu jsou nemocní (pozitivní) jedinci spojeni s nižšími hodnotami než jedinci zdraví (negativní). Prostým inverzním otočením škály testu převedeme body z plochy pod diagonálou do oblasti nad diagonálou, a získáme tak plochu pod křivkou ROC > 0,5.
V literatuře lze nalézt třídění hodnot AUC, které kvantifikuje diagnostickou sílu testů. Podle nejčastěji požívaného členění lze test s AUC nad 0,75 již považovat za uspokojivě diskriminující:
AUC: 0,9–1,0 výborně diskriminující
AUC: 0,8–0,9 velmi dobře diskriminující
AUC: 0,7–0,8 dobře diskriminující
AUC: 0,6–0,7 dostatečně diskriminující
AUC: 0,5–0,6 nedostatečně diskriminující.
Hodnotu AUC lze ovšem při konstrukci křivky ROC přesně odhadnout, a to včetně intervalu spolehlivosti a statistické významnosti. Samotný výpočet samozřejmě v dnešní době ponecháme na statistických programech. Uživatel pouze musí správně zvolit metodu výpočtu, přičemž v základní nabídce jsou metody parametrické a neparametrické. Parametrický výpočet předpokládá existenci tzv. binormálního rozdělení, kdy rozdělení proměnné X, která je výstupem testu, je normální v rámci nemocných i zdravých osob. Takovou situaci schematicky znázorňuje například obr. 1. Bohužel tento předpoklad nemusí být v praxi vždy splněn, rozdělení mohou být asymetrická, normalitu nelze ověřit z důvodu malého vzorku anebo je výstup testu ordinální (příklad 1). V takovém případě vysoce doporučujeme neparametrický odhad plochy pod křivkou, např. pomocí Wilcoxonovy pořadové statistiky. Ukázku neparametrického odhadu přinášíme v číselně zjednodušeném příkladu 2. Doufejme, že poněkud složitější matematické vztahy nejsou odrazující. Smyslem příkladu je doložit, že výpočet lze u menších souborů provést i bez počítače a specializovaného software.
Příklad 1. Výpočet křivky ROC pro ordinální skóre. 
Příklad 2. Využití Wilcoxonovy (Mann-Whitneyovy) statistiky pro odhad plochy pod křivkou ROC (Hanley a McNeil, 1982; Zhou et al, 2002). 
Odhady ploch pod různými křivkami ROC lze nejen doplnit intervalem spolehlivosti, ale také je mezi sebou statisticky srovnat. Nulová hypotéza je zde shoda plochy a výsledek se vyjadřuje pomocí standardní testové statistiky. Zjednodušenou ukázku takového testu přináší příklad 3. K testování jsou často využívány postupy, které stanoví plochu pod každou ROC křivkou a srovnání provedou pomocí modifikovaného Wilcoxonova pořadového testu (Hanley a McNeil, 1982, 1983). Opět zdůrazňujeme, že takto lze srovnat diagnostickou sílu zcela rozdílných testů, jež měří rozdílné proměnné. Křivka ROC je univerzální nástroj současně využitelný pro různé diagnostické postupy (Metz et al, 1998).
Příklad 3. Srovnání plochy pod křivkou ROC u souborů dat (Hanley a McNeil, 1983). 
Další využití křivek ROC představuje validace různých klasifikačních skóre. Body ležící na ROC křivce můžeme interpretovat jako klasifikátory, neboť klasifikují mezi zdravými a nemocnými jedinci s cílem minimalizovat pravděpodobnost nesprávné klasifikace. ROC analýzu lze využít k validaci i poměrně složitých klasifikátorů. Komplexní klasifikátor (vzniklý např. na základě součtu několika parametrů jako integrující rizikové skóre) nabízí ordinální škálu hodnot, které mohou být využity např. k rozlišení dvou skupin pacientů, dvou léčebných postupů apod. Hodnoty ordinální škály lze zpracovat pomocí ROC analýzy, odhadnout plochu pod křivkou a tu srovnat s výsledky, které nabízejí jiné klasifikátory. Aplikace křivek ROC tak dosáhla zobecnění jako nástroj podporující typologii subjektů nebo validaci různých rozhodovacích postupů. Analýza ROC je využívána i při optimalizaci diagnostických a léčebných schémat nebo obecněji managementu nemoci (clinical decision making).
Rovněž při hodnocení dopadu určité klasifikace (např. pacientů podle rizikovosti nemoci) je velmi významným krokem správné nastavení dělicí hranice; opět se můžeme dopustit chyby dvojího druhu, a tedy přijetí nesprávných rozhodnutí (nesprávně pozitivní nebo nesprávně negativní klasifikace). Tyto chyby ale nemusí vždy představovat stejné riziko, resp. nemusí mít stejnou cenu. Jestliže cena falešně pozitivních rozhodnutí je stejná jako cena falešně negativních rozhodnutí, je nejlepší hranice testu taková, kdy k oběma typům nesprávných rozhodnutí dochází se stejnou pravděpodobností. Pokud cena (váha) chyb stejná není, musíme nastavit hraniční bod spíše asymetricky tak, abychom minimalizovali negativní dopad následného rozhodování. K takovým analýzám bývá využívána tzv. ztrátová funkce, kterou stručně představíme jako nástroj k číselnému ohodnocení možných chyb (resp. ohodnocení ztráty, kterou utrpíme, pokud nesprávně zařadíme pozitivní jedince mezi negativní, či naopak). Ohodnocením ztráty nemusí být pouze finance, může jít o číselně vyjádřené riziko komplikací nebo ztráty léčebné odpovědi u pacienta anebo o číselné vyhodnocení poklesu kvality života pacientů apod. Hraniční bod je potom nastavován tak, aby následná rozhodnutí minimalizovala nejzávažnější rizika. Nastavením hraničního bodu ovšem nastavujeme i senzitivitu a specificitu prováděných testů nebo hodnocení.
K vykreslení křivek ROC, k odhadu plochy pod křivkou i k jejich vzájemnému srovnání lze dnes využít řadu statistických nástrojů. V podstatě každý z renomovaných softwarových nástrojů (SPSS, SAS, Statistica for Windows) nabízí algoritmy po tento typ analýz. Čtenářům doporučujeme portál http://metz-roc.uchicago.edu/MetzROC, kde lze získat rozsáhlý přehled literatury o ROC křivkách a také přístup ke specializovanému software, který vyvinul profesor radiologie Charles E. Metz (Metz a Kronman, 1980; Metz et al, 1998).
Na závěr nelze nezmínit poměrně zajímavou historii křivek ROC. K vývoji tohoto metodického konceptu došlo během 2. světové války, konkrétně po útoku Japonska na Pearl Harbour, s cílem posílit diagnostickou a indikační hodnotu radarových signálů. Optimalizovanou diagnostickou hodnotou byla schopnost radaru rozlišit mezi signálem a šumem. Po druhé světové válce se již připravený metodický aparát uplatnil v psychologii při výzkumu vnímavosti lidí a zvířecích modelů vůči různým podnětům. Využití pro validaci diagnostických testů a obdobných rozhodovacích schémat pak bylo dalším logickým krokem. U zrodu ROC analýz tedy stála radiační fyzika a radiologie. ROC křivky zůstaly své mateřské vědě věrné, neboť i dnes jsou využívány pro validaci nových radiodiagnostických metod (Obuchowski, 2003).
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz
Zdroje
Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982; 143 : 29–36.
Metz CE, Kronman HB. Statistical significance tests for binormal ROC curves. J Math Psychol 1980; 22 : 218–243.
Metz CE, Herman BA, Shen JH. Maximum-likelihood estimation of ROC curves from continuously--distributed data. Statistics in Medicine 1998; 17 : 1033–1053.
Obuchowski NA. Receiver operating characteristic curves and their use in radiology. Radiology 2003; 229 (1): 3–8.
Zhou XH, Obuchowski NA, McClish DA. Statistical methods in diagnostic medicine. 1st ed. New York: Wiley-Interscience 2002.
Hanley JA, McNeil BJ. A method of comparing the areas under receiver operating characteristic curves derived from the same cases. Radiology 1983; 148 : 839–843.
Štítky
Dětská neurologie Neurochirurgie Neurologie
Článek vyšel v časopiseČeská a slovenská neurologie a neurochirurgie
Nejčtenější tento týden
2011 Číslo 4- Rozpoznejte periferní neuropatii – dotazník pro pacienty, podpora pro lékaře
- Tři jsou více než jeden: Kombinace 3 vitaminů skupiny B prodlužuje délku neuritů
- Generalizovaná úzkostná porucha, její diagnostika a léčba
- Vitamin B12 − mnoho různých forem, žádný rozdíl v absorpci
-
Všechny články tohoto čísla
- Porucha pozornosti s hyperaktivitou (attention deficit/hyperactivity disorder – ADHD)
- Neurální komponenty motivačních a rozhodovacích procesů v lidském mozku
- Histopatologická diagnostika mitochondriálních myopatií – indikace a přínos svalové biopsie
- Vztah genotypu apolipoproteinu E ke klinickému průběhu a následkům poranění mozku u dětí a mladistvých
- Výskyt mutácií v géne Leucine rich repeat kinase 2 u pacientov s Parkinsonovou chorobou na Slovensku
- Glatiramer acetát (Copaxone®) v léčbě atakovité formy roztroušené sklerózy mozkomíšní – klinická účinnost a bezpečnostní profil
- Opožděný akutní subdurální hematom
- Víčkové implantáty v terapii lagoftalmu
- Kognitivní účinky dlouhodobé léčby subkutánními apomorfinovými infuzemi u pacientů s pokročilou Parkinsonovou nemocí
- Vrozená myotonie na podkladě mutací v genu pro chloridový kanál ClC-1
- Opakovaná intradetruzorová aplikace botulinumtoxinu A u dětí s hyperaktivitou detruzoru
- Radikulopatia spôsobená lumbálnymi epidurálnymi varixami – kazuistika
- Dehiscence stěny kanálu a výhřez lícního nervu – kazuistiky
- Spinální komplikace u genetických syndromů – kazuistiky
- Neurologické komplikace při onemocnění herpes zoster – kazuistika
- K životnímu jubileu primářky MUDr. Evy Urbánkové
- Webové okénko
-
Analýza dat v neurologii
XXVIII. Hodnocení diagnostických testů – křivky ROC - Aktuální informace o postgraduálním vzdělávání
- Česká a slovenská neurologie a neurochirurgie
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Porucha pozornosti s hyperaktivitou (attention deficit/hyperactivity disorder – ADHD)
- Opožděný akutní subdurální hematom
- Neurologické komplikace při onemocnění herpes zoster – kazuistika
- Vrozená myotonie na podkladě mutací v genu pro chloridový kanál ClC-1
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Revma Focus: Spondyloartritidy
nový kurz
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání



