-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaModeling the Effects of Vorinostat Reveals both Transient and Delayed HIV Transcriptional Activation and Minimal Killing of Latently Infected Cells
Combination antiretroviral therapy (cART) for HIV infection must be taken for life due to the existence of long lived latently infected cells. Recent efforts have focused on developing latency reversing agents to eliminate latently infected cells by activating HIV production. In this work, we assess the impact of a latency reversing agent, vorinostat, by fitting dynamic models to data from a clinical trial. Results show that vorinostat treatment induces HIV transcription transiently and that the sustained induction of HIV transcription may depend on the temporal impact of vorinostat on host gene expression. Our results also suggest that vorinostat treatment is not sufficient to induce killing of latently infected cells in a majority of HIV-infected individuals on cART.
Published in the journal: . PLoS Pathog 11(10): e32767. doi:10.1371/journal.ppat.1005237
Category: Research Article
doi: https://doi.org/10.1371/journal.ppat.1005237Summary
Combination antiretroviral therapy (cART) for HIV infection must be taken for life due to the existence of long lived latently infected cells. Recent efforts have focused on developing latency reversing agents to eliminate latently infected cells by activating HIV production. In this work, we assess the impact of a latency reversing agent, vorinostat, by fitting dynamic models to data from a clinical trial. Results show that vorinostat treatment induces HIV transcription transiently and that the sustained induction of HIV transcription may depend on the temporal impact of vorinostat on host gene expression. Our results also suggest that vorinostat treatment is not sufficient to induce killing of latently infected cells in a majority of HIV-infected individuals on cART.
Introduction
Treatment of HIV-infected individuals with combination antiretroviral therapy (cART) effectively suppresses HIV to levels below the limit of detection of conventional assays and substantially reduces morbidity and mortality of HIV infected patients [1]. However, it does not eradicate the virus and treatment is lifelong [2]. Therefore, developing novel therapeutics to cure HIV infection remains an important research priority [3,4]. A major barrier to cure is the presence of a population of long lived latently infected cells [4] that can persist indefinitely in patients treated with highly potent cART [5]. Recent efforts have focused on strategies that activate HIV production in latently infected cells. The idea, termed ‘shock and kill’ [6], is to first shock latently infected cells thereby activating HIV gene expression, such that the cells are then killed by viral cytopathic effects or immune-mediated cell death. Histone acetylation is one of several factors that regulate HIV transcription and is therefore important for establishing and maintaining latency [7]. Drugs such as histone deacetylase inhibitors (HDACi) enhance acetylation of both histones and proteins and thereby induce changes in gene transcription, including transcription of HIV [8].
Vorinostat, a histone deacetylase inhibitor licensed for the treatment of cutaneous T-cell lymphoma [9], has been shown to activate HIV transcription in resting memory CD4+ T-cells in vivo [10,11]. In a recent clinical trial, 20 HIV-1 infected individuals on suppressive cART were treated orally with 400 mg a day of vorinostat for 14 days and then followed for an additional 70 days. Overall, vorinostat induced a rapid and sustained increase of cell-associated unspliced (CA-US) HIV RNA [10]. However, the response pattern was highly variable among the participants. For example, in half of the participants, after an initial significant increase in CA-US HIV RNA, the level of CA-US HIV RNA decreased rapidly within 1–3 days before increasing again, and in 14 of the 20 participants, the level of CA-US HIV RNA continued to increase after vorinostat was stopped. These puzzling observations raise important questions about the temporal impact of vorinostat treatment on HIV transcription and the design of treatment strategies to eradicate the latent reservoir.
We constructed mathematical models to better understand the temporal changes in CA-US HIV RNA in individuals treated with vorinostat. Mathematical models have been widely applied to study viral dynamics in vivo [12–14]. They played an instrumental role in quantifying important parameters, such as the half-lives of virions and infected cells in vivo [14]. Recently, several models have been developed to understand the maintenance of the latent reservoir under cART treatment [15–17], the viral rebound time distribution after latency reversing agent (LRA) treatment [18], and the optimal time to start a LRA [19]. However, the dynamic response of HIV transcription in latently infected cells following treatment with a LRA has not been investigated. This question has important implications for future clinical trial design and optimizing treatment strategies to eliminate latently infected cells. Previous models have generally assumed that the HIV provirus in latently infected cells becomes fully activated following treatment with a LRA and that subsequent events will be identical to latently infected cells activated by normal immunological signals or through the T-cell receptor [18,19]. However, evidence suggests that current LRA treatments primarily activate HIV transcription and its impact on translation may be mild or minimal [20,21]. Here, we construct models that treat cells activated by a LRA and naturally activated cells separately. By fitting models to the clinical data, we show the complex dynamic response of latently infected cells to vorinostat can be explained. Furthermore, we use the models to quantify the extent to which vorinostat activates HIV transcription and induces cell death in vivo.
Results
Direct Activation Model
We first construct a mathematical model based on a previously published latency model by Rong et al. [15]. As the study participants were treated with suppressive cART for a medium of 5 years, we have chosen parameters in the Rong et al. model such that before vorinostat treatment the viral load is approximately 5 HIV RNA copies/ml, target cells levels are 750 T cells/μL similar to mean CD4 count in the 20 clinical trial subjects [10] and latently infected cell levels are 2/mL, which is approximately 2.7/million CD4 cells (roughly consistent with previous studies [22,23]). The major innovation in the direct activation model is that we assume latently infected cells become transcriptionally induced and express CA-US HIV RNA directly upon vorinostat treatment (Fig 1A; see Methods for full description of the model and Table 1 for parameter values). Thus, two equations are added to the Rong et al. model [15], one for the number of cells that have HIV transcription induced by vorinostat, LA, and one for the average amount of CA-US HIV RNA per transcriptionally activated cell, R. Also, cells that are transcriptionally induced by vorinostat are assumed to be in a different state than cells that are naturally activated.
Fig. 1. Schematic illustrations of two latency models that describe the impact of vorinostat treatment. 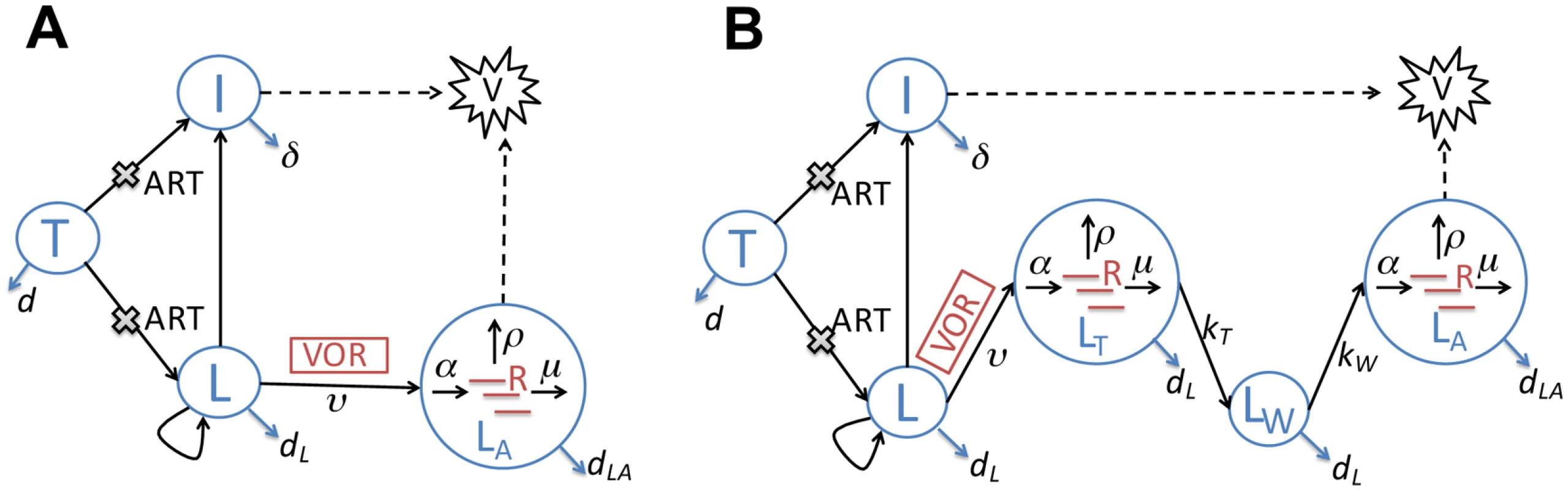
The models keep track of both the within-host infection dynamics and intracellular HCV transactivation dynamics. (A) The direct activation model. CD4+ target cells (T) can be infected by HIV (V). Upon infection, the majority of infected target cells become productively infected cells (I), while a small fraction become latently infected cells (L). Latently infected cells (L) undergo asymmetric division and their progeny can either be activated or remain latent. Under vorinostat treatment, the latently infected cells become sustainably activated (LA) at rate ν. In these cells, CA-US HIV RNAs (R) are produced at rate α, exported at rate ρ and degraded at rate μ. Combination antiretroviral therapy (cART) with reverse transcriptase and protease inhibitors inhibits infection and production of infectious virus. (B) The delayed activation model. This model extends the direct activation model by adding two additional states: latently infected cells that are transiently activated (LT) upon vorinostat treatment, and cells that were transiently activated and now are in a waiting state (LW), i.e. a period of delay, before transitioning to a sustained activation state (LA). CA-US HIV RNAs (R) are produced from both the transiently activated cells (LT) and the sustainably activated cells (LA). Key rate constants are shown on the transitions (arrows) between compartments (see Table 1 for notation). Tab. 1. Description of parameters and fixed parameter values in the model. 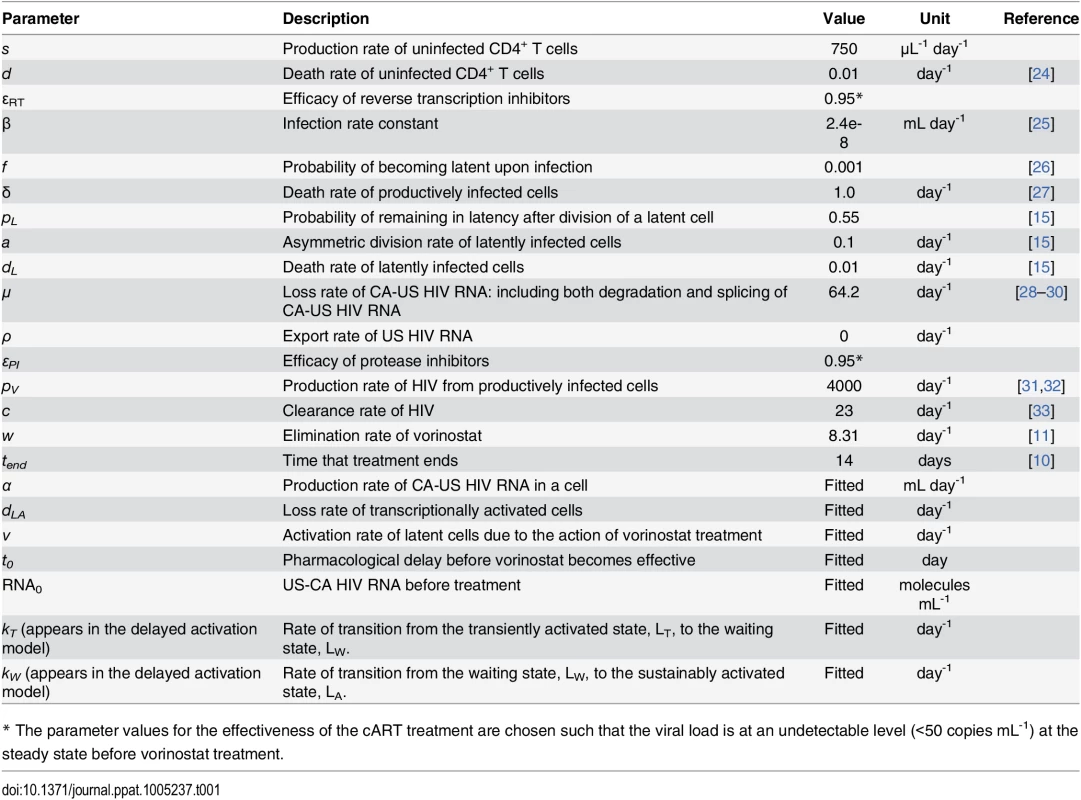
* The parameter values for the effectiveness of the cART treatment are chosen such that the viral load is at an undetectable level (<50 copies mL-1) at the steady state before vorinostat treatment. We fitted this model to the clinical data collected during the entire 84-day study period (see Methods for the fitting procedure and S1 Table for best-fit parameter values). In general, the direct activation model does not explain the data well especially during the first 1–3 days’ treatment (S1 Fig) and the period after treatment stops (S2 Fig). First, in 10 of the 20 participants, the level of CA-US HIV RNA first increased upon initiation of vorinostat, and then decreased rapidly after the first 1–3 days, whereas the best-fit model curves in these patients have CA-US HIV RNA increasing continuously during vorinostat treatment. Second, in 14 out of the 20 participants, the level of CA-US HIV RNA increased at variable time points after cessation of vorinostat at day 14, whereas the model predicts that the level always decreases over time after cessation of vorinostat.
To better understand the initial peaking pattern observed in half of the study participants soon after the initiation of vorinostat, we fitted the model to data obtained during the first 7 days of treatment only (Fig 2). The peaking pattern was well described by the model in five participants (VOR001, VOR004, VOR010, VOR016, VOR018). In these individuals, the estimated loss rate of transcriptionally activated cells, dLA, ranged between 1.8 and 10 day-1 (see S2 Table), and is much greater than the death rate of productively infected cells, i.e. 1.0 day-1 [27]. Rates of decrease of CA-US HIV RNA levels higher than 1.0 day-1 were also apparent in 5 other participants (VOR008, VOR019 and VOR021-023). This decrease can potentially result from either death of cells transcriptionally activated by vorinostat or from shutdown of HIV transcription and loss of CA-US HIV RNA. We reason that this decline is not due solely to cell death, as it is unlikely that cells activated by vorinostat die at a faster rate than productively infected cells. Then why would HIV transcription shut down during vorinostat treatment?
Fig. 2. Fitting results of the direct activation model to the clinical data from the first 7-day’s of treatment. 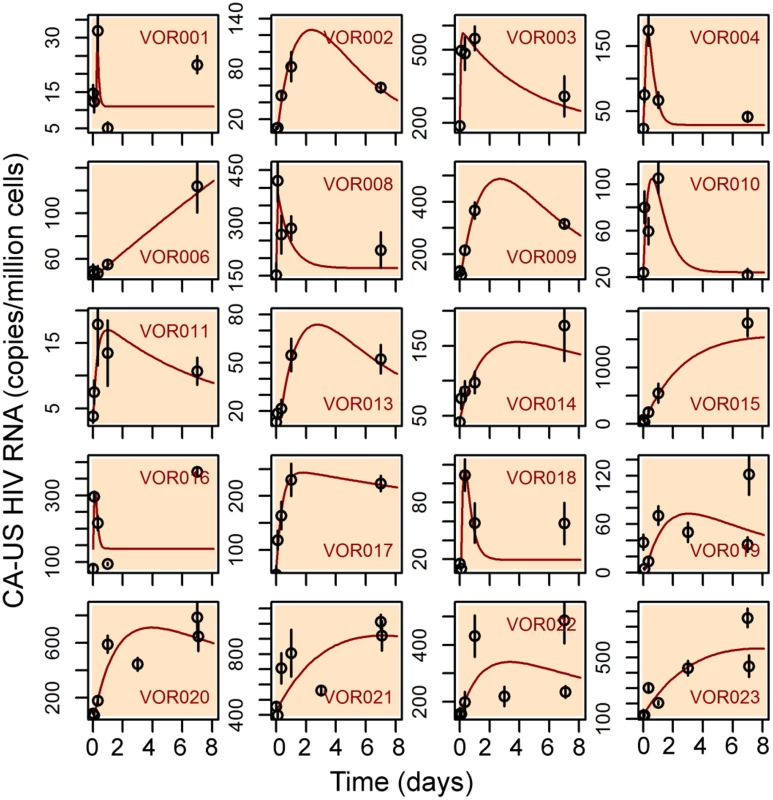
Each panel shows the fitting result for a participant. Red lines are model simulations using best-fit parameter values. The black circles and vertical black lines are the mean and standard deviation of four replicate measurements made at each time point. Previous in vitro studies have shown the activation of HIV transcription is a transient stochastic process, and that the duration of this transient process is dependent on the strength of Tat transcriptional feedback [34–36], as well as the availability and regulation of many host factors that are necessary for transcriptional activation, such as the NAD-dependent deacetylase sirtuin-1, NF-κB, Yin Yang 1 and the positive transcription elongation factor, P-TEFb [37–41]. In latently infected cells, mostly memory T cells, these transcription factors are likely to be at low levels [42–44], whereas many host enzymes such as Murr1 (a gene product that restricts HIV-1 replication), human schlafen 11 and the lipid raft associated protein tetherin, actively inhibit HIV transcription initiation [45], mRNA translation [46], and viral release [47]. Therefore, before vorinostat treatment, the host factors/enzymes required for full HIV gene activation are most likely limiting in latently infected cells. After vorinostat treatment initiation, host genes undergo rapid differential regulation at 2, 8 and 24 hours [10]; however, the immediate impact of vorinostat treatment may not be sufficient to induce HIV gene transcription sustainably. This unfavorable cellular environment and rapid changes in gene expression may lead to very short transcriptional pulses of Tat activity and CA-US HIV RNA production. Without further production of CA-US HIV RNA, the rapid decrease observed in the data may be a result of the loss of US HIV RNA by degradation and by splicing.
Delayed Activation Model
Vorinostat treatment not only induces rapid changes in host gene expression but also induces changes after treatment cessation [10]. It is therefore plausible that the late increase in HIV transcription after vorinostat treatment is due to a longer-term impact on host gene transcription. To test this hypothesis, we extended the direct activation model to include a ‘transiently activated’ state (LT) and a ‘waiting’ state (LW), and denote this as the ‘delayed activation’ model. We assume that upon vorinostat treatment latently infected cells first get activated transiently, i.e., enter the transient activation state, LT, where CA-US HIV RNAs are produced for a short period of time. We assume the cells then enter a waiting state, LW, in which there is no CA-US HIV RNA production before becoming sustainably activated cells, LA (Fig 1B). The waiting state reflects the time needed for the transcriptional programs to produce sufficiently high levels of host factors necessary for transcriptional activation such that the cellular environment becomes favorable for sustained HIV transcription. We assume that the cells in the transiently activated state and in the waiting state die at the same rate as in the latent state (L) as transient activation is not likely to be strong enough to produce the shock needed for kill. The ordinary differential equations (ODEs) describing this model are given in the Methods.
Next, we tested whether the above hypotheses explain both the short-term and the long-term dynamics of CA-US HIV RNAs by fitting the delayed activation model to the full data set (see S3 Table for best-fit parameter values), and found that the delayed activation model describes the data much better than the direct activation model in a majority of participants (compare S3 and S4 Figs with S1 and S2 Figs, respectively). It successfully describes the initial pattern of CA-US HIV RNA change following initiation of vorinostat in most individuals as well as the dynamics of CA-US HIV RNA in 6 of the 14 individuals where the level of CA-US HIV RNA increased after cessation of vorinostat. For the other 8 patients, the delayed activation model does not predict the magnitude of the late increase in CA-US HIV RNA level at some time points (S4 Fig). We speculate that the discrepancy may arise from the assumption of an exponentially distributed residence time for latently infected cells in the waiting state before becoming sustainably activated (an assumption implicitly assumed in the ODE system). This assumption is valid when a single event is needed for the transition to sustained activation. However, it is likely that multiple events must occur before the transition to sustained activation, such as upregulation of several host factors, HIV RNA splicing and expression of tat and other regulatory proteins including rev.
Multistage Delayed Activation Model
We, thus, further modified our model to assume that cells in the waiting state have to go through several stages before becoming sustainably activated as in previous work describing the multiple events needed to drive an initially infected cell into viral production [48]. We denote this model the ‘multistage delayed activation’ model and the equations describing this model are given in the Methods. See Table 2 for a summary of the assumptions made with regard to the impact of vorinostat on latently infected cells in the three different models.
Tab. 2. Comparison of assumptions made in the direct activation, the delayed activation, and the multistage delayed activation model. 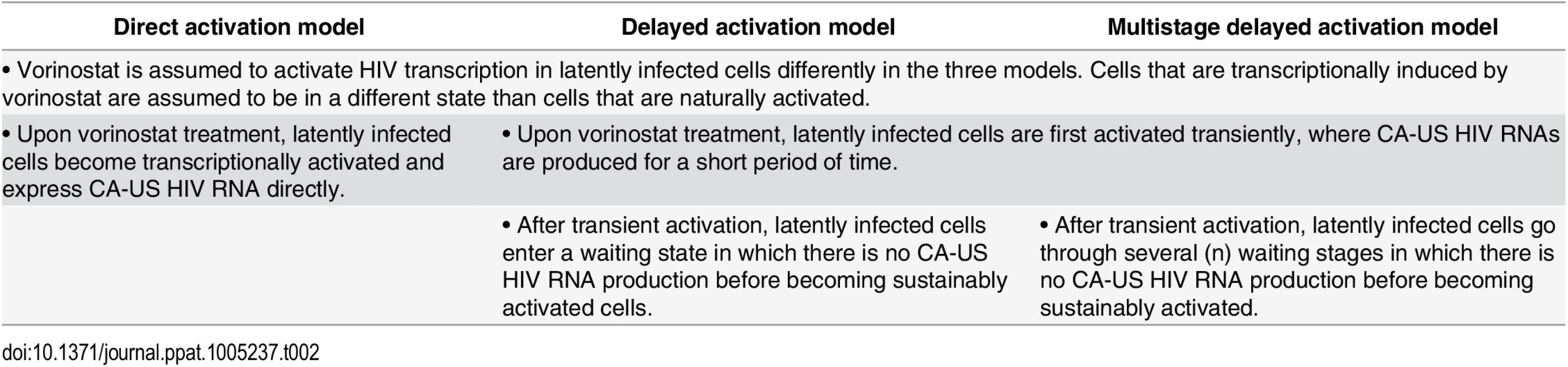
In this model, the LW state is divided into n identical sub-states, i.e. LW,1, LW,2, … LW,n. The transition rate from one sub-state to the next is set to nkw such that the average residence time in the overall waiting state is 1/kw. This model is equivalent to one in which we assume the transition out of the waiting state is stochastic with the delay described by a gamma probability distribution [49]. We let n change from 1 to 10, and fitted these 10 model variants to the clinical data from all 20 participants (S5 Fig). The fitting results show that this multistage delayed activation model describes the patterns of increases of CA-US HIV RNA after cessation of vorinostat as well as the initial peak following initiation of vorinostat (Fig 3 and S6 Fig; see S4 Table for best-fit parameter values).
Fig. 3. The multistage delayed activation model describes the clinical data well in a majority of the participants. 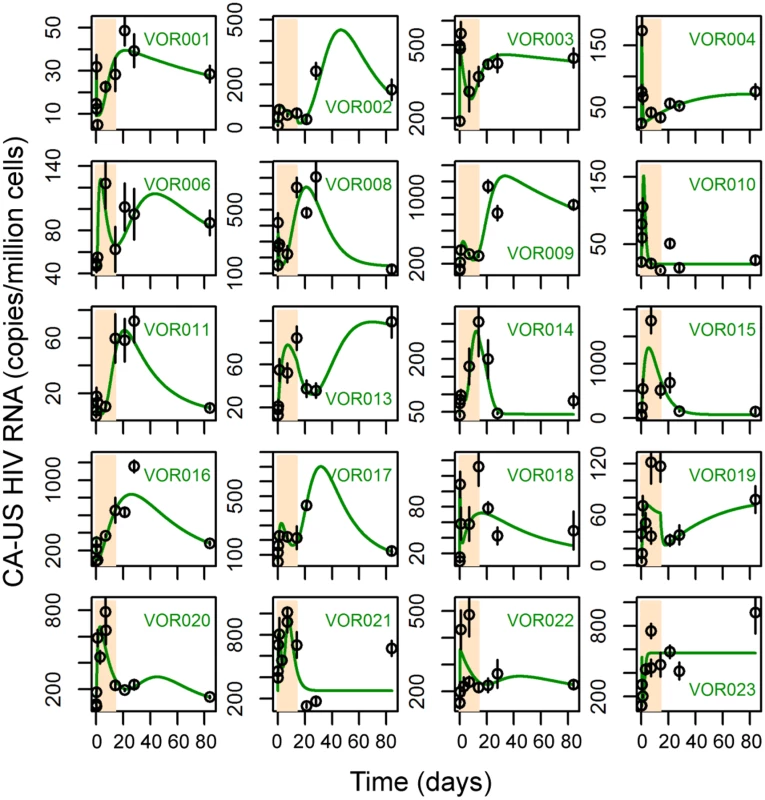
Each panel shows the simulation trajectories using best-fit parameters of the multistage delayed activation model (green lines) and the levels of CA-US RNA measured in the clinical trial. The period of vorinostat treatment is shaded in bisque. We further performed model selection using the corrected Akaike information criterion (AICc) (see Methods). The direct activation model significantly underperformed compared to the delayed activation model and the multistage delayed activation model in 19 out of the 20 participants. The multistage delayed activation model was significantly better than the delayed activation model in 12 participants (Table 3). These results support the hypothesis that the immediate impact of vorinostat treatment is to activate HIV transcription for a short period of time (1–3 days), possibly due to the limited availability of many host cellular factors and that sustained activation may take longer to attain and a number of events (possibly in host cell transcriptional regulation) must occur before sustained HIV transcription becomes possible. As the number of events required varied among the participants, cells in different individuals may be in different states of latency. Also, host gene expression patterns, which can differ among individuals, may play a role in determining the length of the delay. Analyzing the effect of changing the number of waiting stages on the model fit to the data using AICc shows that for 17 out of the 20 participants, using a model with more than 7 stages would be a good choice in general (S5 Fig).
Tab. 3. The average residual sum of squares per data point (RSS/n) and relative AICc (ΔAICc) scores for the direct activation model, the delayed activation model and the multistage delayed activation model fit to the data in 20 patients. 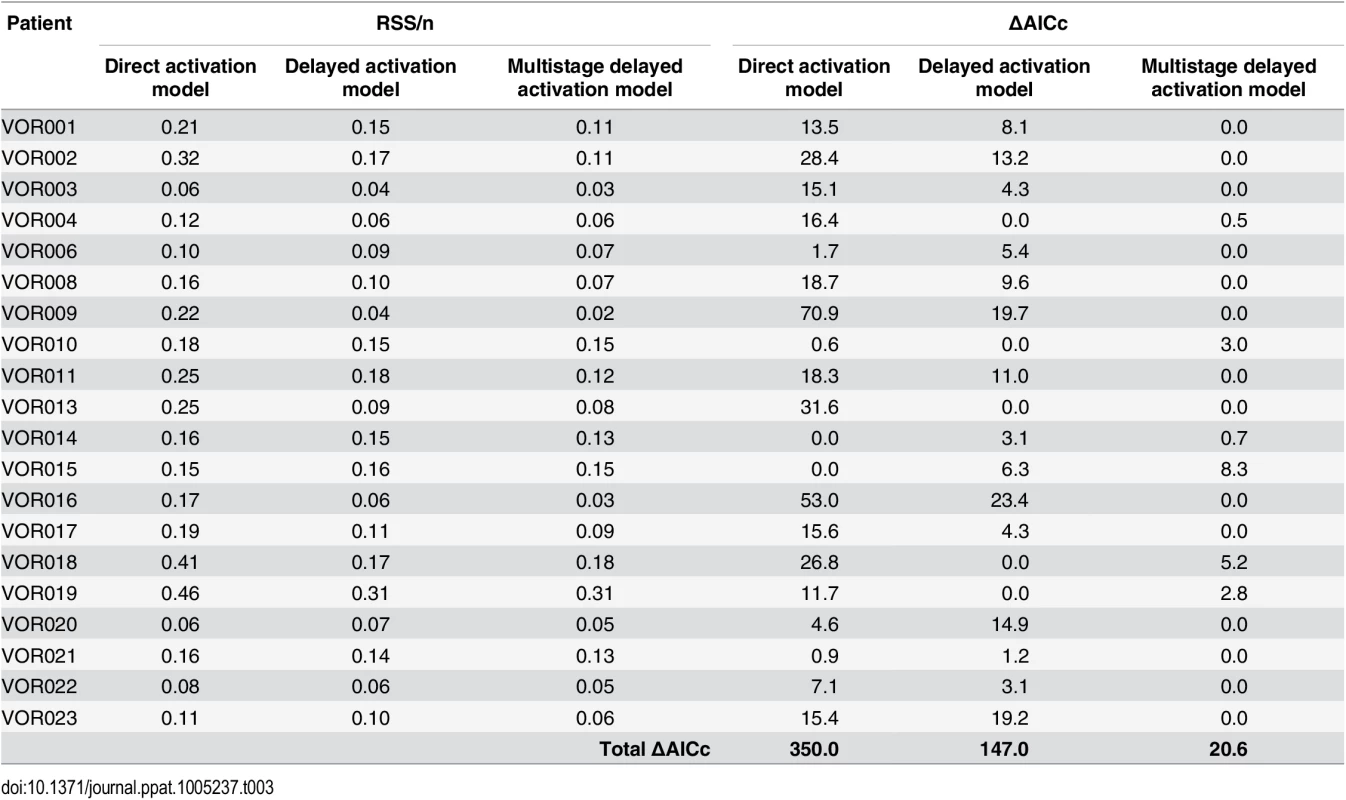
ΔAICc scores are calculated as the difference between the AICc score of a model and the AICc score of the best model in each patient, respectively. Thus ΔAICc = 0 indicates the best model. The total ΔAICc score is calculated as sum of ΔAICc scores in all 20 patients, where the lowest total ΔAICc indicates the best overall model. Quantitative Impact of Vorinostat Treatment on Latently Infected Cells
We next examined the best-fit parameter values of the multistage delayed activation model to assess the impact of vorinostat on latently infected cells in vivo. First, we find that the estimated values of α, the rate of CA-US HIV RNA production induced by vorinostat in latently infected cells, varies over a wide range (over 1.5 logs) among the 20 patients, suggesting the response to vorinostat is very heterogeneous across participants. In a majority of patients, the estimated values of α are smaller than the production rate of CA-US HIV RNA in productively infected cells, αI (Fig 4A; see Methods for calculation of αI). We then examined the estimated loss rate of transcriptionally activated latently infected cells, dLA, and found that in 12 participants the estimated loss rates are extremely low, close to the death rate of latently infected cells, dL (Fig 4B). Although the estimated loss rates are higher than dL in other patients, we were not able to distinguish whether the loss is through shutdown of HIV transcription or through cell death. Nonetheless, the low estimates of the loss rate in most participants suggest that vorinostat treatment does not induce killing of transcriptionally activated latent cells in vivo in a majority of individuals, and thus, according to this model, the reductions in reservoir size were minimal or absent in most participants.
Fig. 4. Distributions of best-fit values for the production rate of CA-US HIV RNA and the loss rate of sustainably activated cells in the 20 study participants. 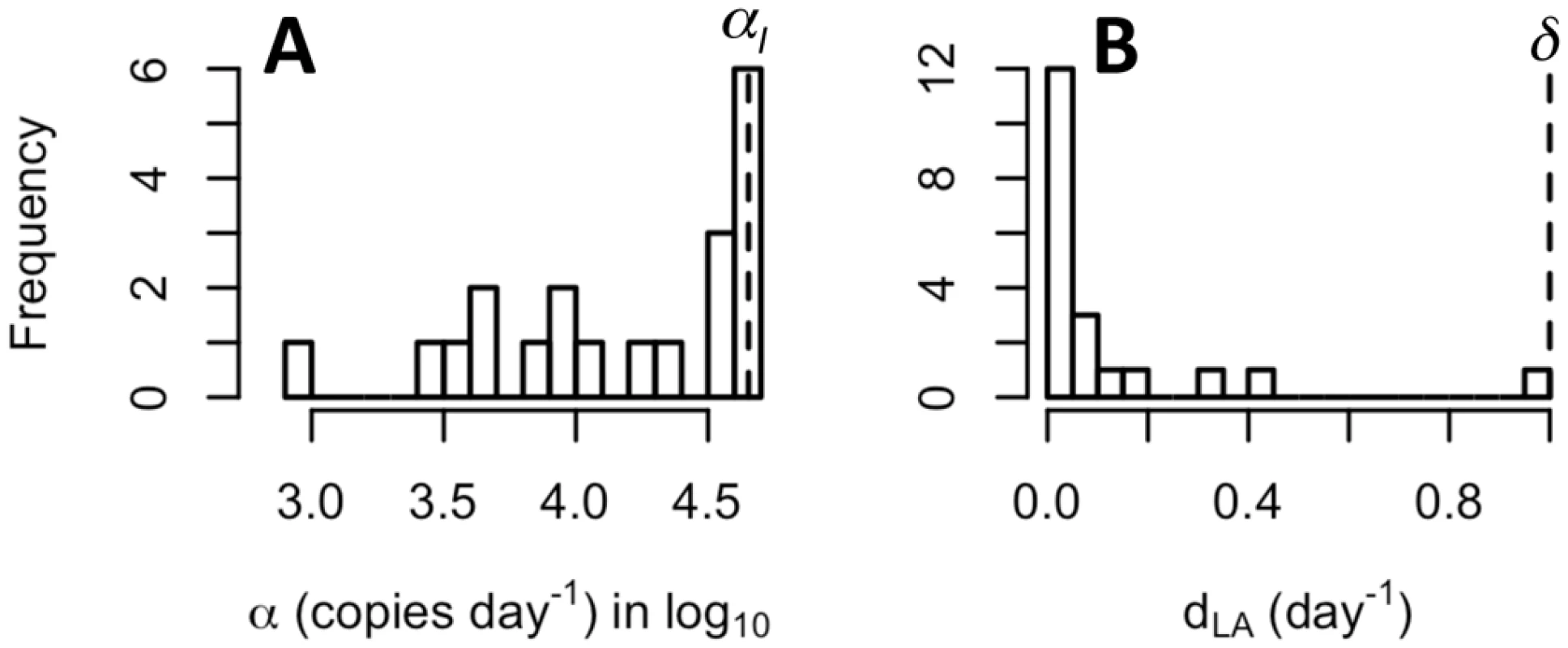
(A) The estimated production rates of CA-US HIV RNA, α, (in Log10) in transcriptionally activated latent cells. Dashed line shows the estimated production rate of CA-US RNA in productively infected cells, αI = 4x104 molecules day-1 [28] (see Methods). (B) The estimated loss rates of sustainably activated cells (LA), dLA. Dashed line shows the death rate of productively infected cells, δ = 1.0 day-1 [27]. We further tested the robustness of the parameter estimates to variations in our assumptions. First, we varied the values of two fixed parameter values that describe the intracellular dynamics of CA-US HIV RNAs, i.e. the rate of US HIV RNA export from the cell in the form of virions, ρ, which we initially assumed to be 0, and the combined rate of RNA splicing and degradation, μ. We find the parameter estimates are robust to changes in the value of ρ (S7 Fig), and that the estimated production rate of CA-US HIV RNAs, α, decreases approximately linearly with decreases in μ (S8 Fig). Thus, if the rate of CA-US HIV RNA loss is lower in cells activated by vorinostat than we have estimated, the estimated production rate of CA-US HIV RNA would also be lower. Last, we tested the robustness of our results to the assumption in the Rong et al. (15) model about how the latently infected cell population is maintained by employing a different model based on the work of Kim and Perelson [50] in which the latent population is maintained by homeostatic proliferation rather than asymmetric division (see Methods). We found the model fits to the CA-US HIV RNA data and the estimates of α and dL are largely unaffected (S9 Fig).
Discussion
We have constructed mathematical models to describe the dynamics of CA-US HIV RNA in HIV-infected individuals on ART who received multiple doses of the HDAC inhibitor vorinostat. By fitting these models to a clinical dataset, we have assessed the dynamic response of latently infected cells to vorinostat and estimated the quantitative impact of vorinostat on the latently infected cell population.
Model analyses show that the multistage delayed activation model, can describe both the short-term and the long-term patterns of change in CA-US HIV RNA induced by vorinostat in most individuals. This model assumes that in response to vorinostat treatment, HIV transcription in latently infected cells is induced transiently. Afterwards, the cells rather than returning to their original latent state go through several waiting stages where CA-US HIV RNAs are not produced but host gene expression patterns may change before becoming sustainably induced. The sustained induction of HIV transcription may even occur after vorinostat treatment is stopped. The induction of HIV gene expression depends on the availability of the HIV Tat protein as well as many host factors [34–36,42–44]. In latently infected cells, the number of Tat proteins [34] and the host factors necessary for inducing HIV transcription, such as P-TEFb, are likely to be at low levels [42–44], and at the same time, the presence of inhibitory molecules, such as Murr1, human schlafen 11 and tetherin, prevent transcriptional activation [45–47] before and at the early stage of response to vorinostat treatment. A recent proteomics and transcriptomics study showed that after 24 h of vorinostat treatment of primary CD4+ T cells the expression of a large number of host genes and proteins as well as genes and proteins previously reported to be involved in HIV transcription was modulated, with some effects appearing to be stimulatory and others inhibitory for HIV reactivation [51]. Therefore, it is likely that the immediate impact of vorinostat on histone acetylation and host gene transcription lead only to a transient induction of HIV RNA transcription and sustained HIV transcription may depend on the longer-term impact of vorinostat on host gene transcription [10]. This delay in sustained transcriptional induction may explain the later increase in the level of CA-US HIV RNA after cessation of vorinostat seen in this study, and the observed refractory periods in response to multiple doses of vorinostat in another study [52]. Note that the effect of vorinostat on host genes may also include the generation of read through transcripts containing HIV RNA [53], but a recent report suggests such transcripts are a minor fraction of total gag RNA [54].
Analyzing the model, we found that the number of stages latently infected cells goes through the waiting state and the total waiting period before sustained induced transcription varied among individuals. This suggests that latently infected cells in different individuals may be in different states, possibly due to variations in Tat protein copy number, host gene expression or alternatively different degrees of chromatin silencing or configuration potentially dependent on the sites of HIV integration. This, in turn, would cause responses to vorinostat to be heterogeneous. Interestingly, the maximal fold increase of CA-US HIV RNA was strongly correlated with the basal level of CA-US HIV RNA before vorinostat treatment [10]. Thus, it is plausible that the basal level of CA-US HIV RNA serves an indicator of the status of latency in a patient and the ease of induction of transcription using LRAs, suggesting that future treatment strategies may be able to be tailored to individual patients.
We further assessed the impact of vorinostat on the rate of loss of cells in the sustained activated state. This estimated loss rate, which serves as an upper bound on the death rate of activated cells (as cells could lose their activated state), is extremely low in most individuals, suggesting that vorinostat treatment does not induce killing of transcriptionally activated cells in most participants. This is in agreement with several previous in vitro and ex vivo studies showing vorinostat activates HIV transcription in only a subset of cells and that this level of HIV transcription and protein expression does not lead to cell death [21,52,53,55,56]. Interestingly, a recent in vitro study showed that vorinostat treatment only has significant impact on HIV transcriptional activation, with the impact on translation being minimal, suggesting that HIV proteins may not be produced sufficiently to lead to virion production or to induce viral cytopathic or cytotoxic T cell mediated cell death [20]. Thus, new treatment strategies aiming at both transcriptional and translational activation of HIV may be needed to induce efficient killing of latently infected cells.
In the model, we have assumed that in each participant, latently infected cells are a homogeneous population and respond to vorinostat by going through two activation steps. However, because of limited data sampling there could have been additional transient activation steps that we were unable to detect. In addition, the latent state of individual infected cells in vivo may differ [57] and it is possible that within an individual, some cells go through a different number of activation steps or have different waiting periods before becoming sustainably activated. This may give rise to the minor discrepancies between the data and the model seen in some participants (VOR010, VOR018, VOR019, VOR021, VOR023 in Fig 3). Although a model that accounts for different responses of latently infected cell subpopulations or has additional activation steps might explain the data, such a model would have more unknown parameters than our current model with only a marginal improvement in model fit. Nonetheless, the possibility that there exist different cell populations in individual patients in terms of their response to vorinostat or additional activation steps cannot be excluded. Further experiments examining the dynamics of host factors/enzymes that are responsible for transcriptional activation and inhibition under LRA treatment could validate our model, improve our understanding of the impact of vorinostat, and ultimately aid the design of treatment strategies to eradicate the latent reservoir.
To conclude, our results suggest that vorinostat induces both immediate transient induction and delayed sustained induction of HIV transcription. Similar dynamic patterns of CA-US HIV RNA were also observed in clinical trials of the LRAs panobinostat and romidepsin [58,59], suggesting LRAs may induce both transient and delayed transcription activation in latently infected cells in general. Therefore, designing clinical trials with frequent longitudinal sampling during both treatment and the follow-up period would help quantify the impact of LRAs. To our knowledge, our work represents the first mathematical model to assess the impact of a LRA on the dynamics of CA-US HIV RNA in vivo. Our model can be easily adapted to study other LRAs as well as combinations of these agents once data are available. In addition, our model or variants of it could be used to assess the efficacy of different candidate treatments, such as those using anti-HIV monoclonal antibodies combined with LRAs, and ultimately suggest optimal drug combinations to eliminate latently infected cells in HIV-infected individuals.
Methods
Clinical Data
As described by Elliot et al. [10], 20 chronically HIV-infected adults receiving at least three antiretroviral agents, having plasma HIV RNA < 50 copies per mL for at least three years (excluding single viral ‘blips’), a CD4+ T-cell count > 500 cells/μL and documented subtype B HIV-1 infection were recruited into a vorinostat trial (ClinicalTrials.gov, NCT01365065). Participants received vorinostat 400 mg orally once daily for 14 days. Levels of CA-US HIV RNA were measured in peripheral blood mononuclear cells at 0, 2, 8 and 24 hours, and on days 7, 14, 21, 28 and 84 (as well as on day 3 for participants VOR019-023). For each blood sample, four replicate q-PCR runs were performed to measure the levels of CA-US HIV RNA. The total number of data points in each patient ranges from 35 to 44.
The Direct Activation Model
The ordinary differential equations (ODEs) describing the model are:
In this model, target cells, T, are produced at a constant rate, s, and die at per capita rate, dT. In the absence of cART, they are infected at per capita rate, βVI, where β is a rate constant and VI is the concentration of infectious virus. The effect of reverse transcriptase inhibitors (RTI) is to multiply the rate of infection by the factor 1-εRT, where εRT is the effectiveness of the RTI with 0 ≤ εRT ≤ 1. Under protease inhibitor treatment, a fraction, εPI, of produced viruses are non-infectious (VNI). Upon infection with viruses, a fraction, f, of infected cells becomes latently infected, and the remaining fraction, 1-f, becomes productively infected. Productively infected cells, I, die at per capita rate, δI1.44, where the power 1.44 models the effects of both viral cytopathicity and cell-mediated immune responses [60,61].
We assume that latently infected cells, L, when activated by antigen at rate a, undergo an asymmetric division in which a daughter cell remains in latency with probability, pL, and becomes productively infected and produces virus with probability, 1-pL [15]. Latently infected cells die at per capita rate, dL. We assume that vorinostat causes latently infected cells to move into a transcriptionally activated state, LA, at rate ν. The transcriptionally activated cells are lost at rate, dLA. We also assume there is a pharmacological delay, t0, in the effect of vorinostat upon treatment initiation such that the rate of activation remains 0 when t<t0, and it becomes ν when t0≤t≤14 days. After treatment is terminated, we assume the effectiveness declines exponentially as νe-w(t-14) for t>14 days, where w is the rate at which vorinostat is cleared from the system. We also model the population average of the amount of CA-US HIV RNA (R) within transcriptionally activated cells. We assume that CA-US HIV RNA is produced at a constant rate, α, once vorinostat becomes effective, i.e. when t≥ t0. CA-US HIV RNA is encapsidated and exported as virions at per capita rate, ρ, and lost by degradation and splicing at per capita rate, μ. Here, we assume that the transcriptionally activated cells do not produce mature viral particles, i.e. ρ = 0, because recent work shows that the production of virus from cells treated with vorinostat is minimal [20,53]. As other LRAs may induce viral production, we leave ρ in the model. Viruses are produced from productively infected cells at rate pv and from transcriptionally activated cells at rate ρR (note that ρ is set to 0 for vorinostat). Viruses are cleared at per capita rate c. The amount of CA-US HIV RNAs, US, is calculated as the sum of the basal level of CA-US HIV RNA, US0, and the average number of US HIV RNAs per activated cell, R, multiplied by the number of activated cells, LA.
The Delayed Activation Model
In the delayed activation model, the equations describing the transient activation state, LT, the waiting state, LW, the transcriptionally activated state, LA, and the total number of CA-US HIV RNAs, US, are
where kT and kw are transition rate constants. The ODEs describing other variables are kept the same as in the direct activation model.The Multistage Delayed Activation Model
The ODEs describing the multistage waiting states are:
where the waiting state is divided into n identical sub-states, i.e. LW,1, LW,2, … LW,n. The transition rate from one sub-state to the next is set to nkw, so that the average residence time in the waiting state, 1/kw, is the same as in the delayed activation model. The ODEs describing other variables are the same as in the delayed activation model.A Model Assuming Constant Proliferation of Latently Infected Cells
To test the assumption about how the population of latently infected cells is maintained, we modified the multi-stage delayed activation such that the latently infected cells proliferate at a constant rate as in Kim and Perelson [50] instead of asymmetric division in the main text. The ordinary differential equations (ODEs) describing the productively infected population and latently infected population are shown below and other terms in the model are kept the same as in the main text.
In this model, the latently infected cells becomes activated at per capita rate a and proliferate at per capita rate r. We set a = 0.0088 day-1 according to [62] and r = 0.0183 day-1, such that the half-life of the latent reservoir is 44 months as estimated before [63].
Parameter Values
The fixed parameter values are based on prior work to yield a baseline state with a plasma viral load of 5 copies/mL and a latently infected cell population of ~2 cells/million cells (Table 1). The production and death rates of uninfected CD4+ T cells were chosen to yield a baseline CD4 count similar to the average level in patients in Elliot et al. [10]. Changes in the values of the fixed parameters that govern the dynamics of target cells and productively infected cells do not impact the estimation of the fitted parameters (S10 Fig). This is because cART is so effective that the contribution of new infections to the latent reservoir is negligible over the time period we study here. We also tested the robustness of the parameter estimates against changes in the fixed parameters that govern intracellular HIV transactivation in latently infected cells and to the structure of the model with regard to how latently infected cells proliferate (S7–S9 Figs).
The CA-US HIV RNA production rate in a productively infected cell, αI, is calculated based on the derivations in Ref. [28]. The basal transcription rate in eukaryotic cells is estimated to be approximately 40 nucleotides/s [64]. The HIV genome has around 9500 nucleotides. Thus, the basal production rate of CA-US HIV RNA production can be estimated as 40/9500≈0.0047 s-1≈406 day-1. In the presence of Tat, the transcription is upregulated to 100 fold [65]. Then, the production rate of CA-US HIV RNA in a productively infected cell, α0, can be calculated as approximately 40,000 transcripts day-1. This maybe a minimal estimate if productively infected cells live approximately one day while producing virus, as Chen et al. [32] have estimated that a productively infected cell produces between 40,000 and 55, 000 virions over its lifespan.
Model Fitting and Model Selection
To fit the direct activation model to the data, we varied 5 unknown model parameters: the production rate of CA-US HIV RNA in a transcriptionally activated cell (α), the death rate of transcriptionally activated cells (dLA), the rate of transcriptional activation (ν), the initial delay of vorinostat effectiveness (t0) and the baseline US HIV RNA level (US0). To fit the delayed activation model and the multistage delayed activation model, we allow 2 additional parameters to be estimated (together with the 5 parameters in the direct-activation model): the transition rate, kT, from the transiently activated state to the waiting state, and the transition rate, kw, from one sub-state of the waiting state to the next.
To estimate the parameter values in each model, we first calculate the residual sum of squares (RSS) between model predicted log CA-US RNA level and log transformed data, and then minimize the RSS using the Nelder-Mead algorithm [66]. 1,000 individual fits were performed for each model starting from parameter values randomly sampled within biologically plausible ranges. The parameter values with the smallest RSS among the 1,000 fits are taken as the best-fit parameter values for each model.
We perform model selection using the corrected Akaike information criterion (AICc) to account for the low number of data points (ranges from 35 to 44) for each patient [67]. The AICc score is calculated as
where n is the number of data points and K is the number of fitted parameters. When comparing models, the model with the lowest score is the best model, although small difference in AICc scores, e.g. ≤ 2, is not significant [67].Supporting Information
Zdroje
1. Palella FJ, Delaney KM, Moorman AC, Loveless MO, Fuhrer J, et al. (1998) Declining morbidity and mortality among patients with advanced human immunodeficiency virus infection. New England Journal of Medicine 338 : 853–860. 9516219
2. Phillips AN, Neaton J, Lundgren JD (2008) The role of HIV in serious diseases other than AIDS. AIDS 22 : 2409–2418. doi: 10.1097/QAD.0b013e3283174636 19005264
3. Deeks SG, Autran B, Berkhout B, Benkirane M, Cairns S, et al. (2012) Towards an HIV cure: a global scientific strategy. Nat Rev Immunol 12 : 607–614. doi: 10.1038/nri3262 22814509
4. Richman DD, Margolis DM, Delaney M, Greene WC, Hazuda D, et al. (2009) The challenge of finding a cure for HIV infection. Science 323 : 1304–1307. doi: 10.1126/science.1165706 19265012
5. Siliciano JD, Kajdas J, Finzi D, Quinn TC, Chadwick K, et al. (2003) Long-term follow-up studies confirm the stability of the latent reservoir for HIV-1 in resting CD4+ T cells. Nat Med 9 : 727–728. 12754504
6. Deeks SG (2012) HIV: Shock and kill. Nature 487 : 439–440. doi: 10.1038/487439a 22836995
7. Van Lint C, Emiliani S, Ott M, Verdin E (1996) Transcriptional activation and chromatin remodeling of the HIV-1 promoter in response to histone acetylation. Embo Journal 15 : 1112–1120. 8605881
8. Peart MJ, Smyth GK, van Laar RK, Bowtell DD, Richon VM, et al. (2005) Identification and functional significance of genes regulated by structurally different histone deacetylase inhibitors. Proc Natl Acad Sci U S A 102 : 3697–3702. 15738394
9. Mann BS, Johnson JR, Cohen MH, Justice R, Pazdur R (2007) FDA approval summary: vorinostat for treatment of advanced primary cutaneous T-cell lymphoma. Oncologist 12 : 1247–1252. 17962618
10. Elliott JH, Wightman F, Solomon A, Ghneim K, Ahlers J, et al. (2014) Activation of HIV transcription with short-course vorinostat in HIV-infected patients on suppressive antiretroviral therapy. PLoS Pathog 10: e1004473. doi: 10.1371/journal.ppat.1004473 25393648
11. Archin NM, Liberty AL, Kashuba AD, Choudhary SK, Kuruc JD, et al. (2012) Administration of vorinostat disrupts HIV-1 latency in patients on antiretroviral therapy. Nature 487 : 482–485. doi: 10.1038/nature11286 22837004
12. Nowak M, May R (2001) Virus dynamics: Mathematical principles of immunology and virology.: Oxford University Press. 256 p.
13. Perelson AS, Nelson PW (1999) Mathematical analysis of HIV-1 dynamics in vivo. Siam Review 41 : 3–44.
14. Perelson AS, Neumann AU, Markowitz M, Leonard JM, Ho DD (1996) HIV-1 dynamics in vivo: Virion clearance rate, infected cell life-span, and viral generation time. Science 271 : 1582–1586. 8599114
15. Rong LB, Perelson AS (2009) Asymmetric division of activated latently infected cells may explain the decay kinetics of the HIV-1 latent reservoir and intermittent viral blips. Mathematical Biosciences 217 : 77–87. doi: 10.1016/j.mbs.2008.10.006 18977369
16. Rong L, Perelson AS (2009) Modeling HIV persistence, the latent reservoir, and viral blips. J Theor Biol 260 : 308–331. doi: 10.1016/j.jtbi.2009.06.011 19539630
17. Rong L, Perelson AS (2009) Modeling latently infected cell activation: viral and latent reservoir persistence, and viral blips in HIV-infected patients on potent therapy. PLoS Comput Biol 5: e1000533. doi: 10.1371/journal.pcbi.1000533 19834532
18. Hill AL, Rosenbloom DI, Fu F, Nowak MA, Siliciano RF (2014) Predicting the outcomes of treatment to eradicate the latent reservoir for HIV-1. Proc Natl Acad Sci U S A 111 : 13475–13480. doi: 10.1073/pnas.1406663111 25097264
19. Petravic J, Martyushev A, Reece JC, Kent SJ, Davenport MP (2014) Modeling the timing of antilatency drug administration during HIV treatment. J Virol 88 : 14050–14056. doi: 10.1128/JVI.01701-14 25253352
20. Mohammadi P, di Iulio J, Munoz M, Martinez R, Bartha I, et al. (2014) Dynamics of HIV latency and reactivation in a primary CD4+ T cell model. PLoS Pathog 10: e1004156. doi: 10.1371/journal.ppat.1004156 24875931
21. Cillo AR, Sobolewski MD, Bosch RJ, Fyne E, Piatak M Jr., et al. (2014) Quantification of HIV-1 latency reversal in resting CD4+ T cells from patients on suppressive antiretroviral therapy. Proc Natl Acad Sci U S A 111 : 7078–7083. doi: 10.1073/pnas.1402873111 24706775
22. Ho YC, Shan L, Hosmane NN, Wang J, Laskey SB, et al. (2013) Replication-competent noninduced proviruses in the latent reservoir increase barrier to HIV-1 cure. Cell 155 : 540–551. doi: 10.1016/j.cell.2013.09.020 24243014
23. Chun TW, Carruth L, Finzi D, Shen X, DiGiuseppe JA, et al. (1997) Quantification of latent tissue reservoirs and total body viral load in HIV-1 infection. Nature 387 : 183–188. 9144289
24. Mohri H, Bonhoeffer S, Monard S, Perelson AS, Ho DD (1998) Rapid turnover of T lymphocytes in SIV-infected rhesus macaques. Science 279 : 1223–1227. 9469816
25. Perelson AS, Kirschner DE, De Boer R (1993) Dynamics of HIV infection of CD4+ T cells. Math Biosci 114 : 81–125. 8096155
26. Jones LE, Perelson AS (2007) Transient viremia, plasma viral load, and reservoir replenishment in HIV-infected patients on antiretroviral therapy. J Acquir Immune Defic Syndr 45 : 483–493. 17496565
27. Markowitz M, Louie M, Hurley A, Sun E, Di Mascio M, et al. (2003) A novel antiviral intervention results in more accurate assessment of human immunodeficiency virus type 1 replication dynamics and T-cell decay in vivo. J Virol 77 : 5037–5038. 12663814
28. Kim H, Yin J (2005) Robust growth of human immunodeficiency virus type 1 (HIV-1). Biophys J 89 : 2210–2221. 16055539
29. Malim MH, Cullen BR (1993) Rev and the fate of pre-mRNA in the nucleus: implications for the regulation of RNA processing in eukaryotes. Mol Cell Biol 13 : 6180–6189. 8105371
30. Blanchard JM, Weber J, Jelinek W, Darnell JE (1978) In vitro RNA-RNA splicing in adenovirus 2 mRNA formation. Proc Natl Acad Sci U S A 75 : 5344–5348. 281684
31. Hockett RD, Kilby JM, Derdeyn CA, Saag MS, Sillers M, et al. (1999) Constant mean viral copy number per infected cell in tissues regardless of high, low, or undetectable plasma HIV RNA. J Exp Med 189 : 1545–1554. 10330433
32. Chen HY, Di Mascio M, Perelson AS, Ho DD, Zhang L (2007) Determination of virus burst size in vivo using a single-cycle SIV in rhesus macaques. Proc Natl Acad Sci U S A 104 : 19079–19084. 18025463
33. Ramratnam B, Bonhoeffer S, Binley J, Hurley A, Zhang L, et al. (1999) Rapid production and clearance of HIV-1 and hepatitis C virus assessed by large volume plasma apheresis. Lancet 354 : 1782–1785. 10577640
34. Razooky BS, Pai A, Aull K, Rouzine IM, Weinberger LS (2015) A hardwired HIV latency program. Cell 160 : 990–1001. doi: 10.1016/j.cell.2015.02.009 25723172
35. Weinberger LS, Dar RD, Simpson ML (2008) Transient-mediated fate determination in a transcriptional circuit of HIV. Nat Genet 40 : 466–470. doi: 10.1038/ng.116 18344999
36. Weinberger LS, Burnett JC, Toettcher JE, Arkin AP, Schaffer DV (2005) Stochastic gene expression in a lentiviral positive-feedback loop: HIV-1 Tat fluctuations drive phenotypic diversity. Cell 122 : 169–182. 16051143
37. Burnett JC, Miller-Jensen K, Shah PS, Arkin AP, Schaffer DV (2009) Control of stochastic gene expression by host factors at the HIV promoter. PLoS Pathog 5: e1000260. doi: 10.1371/journal.ppat.1000260 19132086
38. Pagans S, Pedal A, North BJ, Kaehlcke K, Marshall BL, et al. (2005) SIRT1 regulates HIV transcription via Tat deacetylation. PLoS Biol 3: e41. 15719057
39. Chen L, Fischle W, Verdin E, Greene WC (2001) Duration of nuclear NF-kappaB action regulated by reversible acetylation. Science 293 : 1653–1657. 11533489
40. Barboric M, Nissen RM, Kanazawa S, Jabrane-Ferrat N, Peterlin BM (2001) NF-kappaB binds P-TEFb to stimulate transcriptional elongation by RNA polymerase II. Molecular Cell 8 : 327–337. 11545735
41. Romerio F, Gabriel MN, Margolis DM (1997) Repression of human immunodeficiency virus type 1 through the novel cooperation of human factors YY1 and LSF. J Virol 71 : 9375–9382. 9371597
42. Budhiraja S, Famiglietti M, Bosque A, Planelles V, Rice AP (2013) Cyclin T1 and CDK9 T-loop phosphorylation are downregulated during establishment of HIV-1 latency in primary resting memory CD4+ T cells. J Virol 87 : 1211–1220. doi: 10.1128/JVI.02413-12 23152527
43. Bartholomeeusen K, Fujinaga K, Xiang YH, Peterlin BM (2013) Histone deacetylase inhibitors (HDACis) that release the positive transcription elongation factor b (P-TEFb) from its inhibitory complex also activate HIV transcription. Journal of Biological Chemistry 288 : 14400–14407. doi: 10.1074/jbc.M113.464834 23539624
44. Coiras M, Lopez-Huertas MR, Rullas J, Mittelbrunn M, Alcami J (2007) Basal shuttle of NF-kappaB/I kappaB alpha in resting T lymphocytes regulates HIV-1 LTR dependent expression. Retrovirology 4 : 56. 17686171
45. Ganesh L, Burstein E, Guha-Niyogi A, Louder MK, Mascola JR, et al. (2003) The gene product Murr1 restricts HIV-1 replication in resting CD4+ lymphocytes. Nature 426 : 853–857. 14685242
46. Jakobsen MR, Mogensen TH, Paludan SR (2013) Caught in translation: innate restriction of HIV mRNA translation by a schlafen family protein. Cell Res 23 : 320–322. doi: 10.1038/cr.2012.155 23128674
47. Neil SJ, Zang T, Bieniasz PD (2008) Tetherin inhibits retrovirus release and is antagonized by HIV-1 Vpu. Nature 451 : 425–430. doi: 10.1038/nature06553 18200009
48. Mittler JE, Sulzer B, Neumann AU, Perelson AS (1998) Influence of delayed viral production on viral dynamics in HIV-1 infected patients. Mathematical Biosciences 152 : 143–163. 9780612
49. MacDonald N (1989) Biological delay systems: linear stability theory. Cambridge: Cambridge University Press. 248 p.
50. Kim H, Perelson AS (2006) Viral and latent reservoir persistence in HIV-1-infected patients on therapy. PLoS Comput Biol 2: e135. 17040122
51. White CH, Johnston HE, Moesker B, Manousopoulou A, Margolis DM, et al. (2015) Mixed effects of suberoylanilide hydroxamic acid (SAHA) on the host transcriptome and proteome and their implications for HIV reactivation from latency. Antiviral Res 123 : 78–85. doi: 10.1016/j.antiviral.2015.09.002 26343910
52. Archin NM, Bateson R, Tripathy MK, Crooks AM, Yang KH, et al. (2014) HIV-1 expression within resting CD4(+) T cells after multiple doses of vorinostat. Journal of Infectious Diseases 210 : 728–735. doi: 10.1093/infdis/jiu155 24620025
53. Bullen CK, Laird GM, Durand CM, Siliciano JD, Siliciano RF (2014) New ex vivo approaches distinguish effective and ineffective single agents for reversing HIV-1 latency in vivo. Nat Med 20 : 425–429. doi: 10.1038/nm.3489 24658076
54. Pasternak A, O'Doherty U, Berkhout B (2015) Minor contribution of host-HIV readthrough transcripts to the level of HIV-1 gag RNA. The annual conference on retroviruses and opportunistic infections (CROI). Seattle, Washington.
55. Shan L, Deng K, Shroff NS, Durand CM, Rabi SA, et al. (2012) Stimulation of HIV-1-specific cytolytic T lymphocytes facilitates elimination of latent viral reservoir after virus reactivation. Immunity 36 : 491–501. doi: 10.1016/j.immuni.2012.01.014 22406268
56. Blazkova J, Chun TW, Belay BW, Murray D, Justement JS, et al. (2012) Effect of histone deacetylase inhibitors on HIV production in latently infected, resting CD4(+) T cells from infected individuals receiving effective antiretroviral therapy. J Infect Dis 206 : 765–769. doi: 10.1093/infdis/jis412 22732922
57. Archin NM, Vaidya NK, Kuruc JD, Liberty AL, Wiegand A, et al. (2012) Immediate antiviral therapy appears to restrict resting CD4+ cell HIV-1 infection without accelerating the decay of latent infection. Proc Natl Acad Sci U S A 109 : 9523–9528. doi: 10.1073/pnas.1120248109 22645358
58. Sogaard OS, Graversen ME, Leth S, Olesen R, Brinkmann CR, et al. (2015) The Depsipeptide Romidepsin Reverses HIV-1 Latency In Vivo. PLoS Pathog 11: e1005142. doi: 10.1371/journal.ppat.1005142 26379282
59. Rasmussen TA, Tolstrup M, Brinkmann CR, Olesen R, Erikstrup C, et al. (2014) Panobinostat, a histone deacetylase inhibitor, for latent-virus reactivation in HIV-infected patients on suppressive antiretroviral therapy: a phase 1/2, single group, clinical trial. Lancet HIV 1: e13–21. doi: 10.1016/S2352-3018(14)70014-1 26423811
60. Holte SE, Melvin AJ, Mullins JI, Tobin NH, Frenkel LM (2006) Density-dependent decay in HIV-1 dynamics. J Acquir Immune Defic Syndr 41 : 266–276. 16540927
61. Callaway DS, Perelson AS (2002) HIV-1 infection and low steady state viral loads. Bull Math Biol 64 : 29–64. 11868336
62. Conway JM, Coombs D (2011) A stochastic model of latently infected cell reactivation and viral blip generation in treated HIV patients. PLoS Comput Biol 7: e1002033. doi: 10.1371/journal.pcbi.1002033 21552334
63. Finzi D, Blankson J, Siliciano JD, Margolick JB, Chadwick K, et al. (1999) Latent infection of CD4+ T cells provides a mechanism for lifelong persistence of HIV-1, even in patients on effective combination therapy. Nat Med 5 : 512–517. 10229227
64. Lewin B (2000) Genes VII. New York: Oxford University Press. 990 p.
65. Graeble MA, Churcher MJ, Lowe AD, Gait MJ, Karn J (1993) Human immunodeficiency virus type 1 transactivator protein, tat, stimulates transcriptional read-through of distal terminator sequences in vitro. Proc Natl Acad Sci U S A 90 : 6184–6188. 8327498
66. Nelder JA, Mead R (1965) A simplex-method for function minimization. Computer Journal 7 : 308–313.
67. Burnham KP, Anderson DR (2002) Model selection and multimodel inference: a practical information-theoretic approach. New York: Springer. 488 p.
Štítky
Hygiena a epidemiologie Infekční lékařství Laboratoř
Článek TRIM21 Promotes cGAS and RIG-I Sensing of Viral Genomes during Infection by Antibody-Opsonized VirusČlánek Effector OspB Activates mTORC1 in a Manner That Depends on IQGAP1 and Promotes Cell ProliferationČlánek Fundamental Roles of the Golgi-Associated Aspartyl Protease, ASP5, at the Host-Parasite InterfaceČlánek Modulation of the Surface Proteome through Multiple Ubiquitylation Pathways in African Trypanosomes
Článek vyšel v časopisePLOS Pathogens
Nejčtenější tento týden
2015 Číslo 10- Jak souvisí postcovidový syndrom s poškozením mozku?
- Stillova choroba: vzácné a závažné systémové onemocnění
- Perorální antivirotika jako vysoce efektivní nástroj prevence hospitalizací kvůli COVID-19 − otázky a odpovědi pro praxi
- Diagnostika virových hepatitid v kostce – zorientujte se (nejen) v sérologii
- Diagnostický algoritmus při podezření na syndrom periodické horečky
-
Všechny články tohoto čísla
- Expression of Concern: Misregulation of Underlies the Developmental Abnormalities Caused by Three Distinct Viral Silencing Suppressors in Arabidopsis
- Preparing for the Next Epidemic with Basic Virology
- Effectively Communicating the Uncertainties Surrounding Ebola Virus Transmission
- Translating Basic Research into Clinical Applications: Malaria Research at an NIH Lab
- A Gut Odyssey: The Impact of the Microbiota on Spore Formation and Germination
- Papillomavirus E6 Oncoproteins Take Common Structural Approaches to Solve Different Biological Problems
- Chronobiomics: The Biological Clock as a New Principle in Host–Microbial Interactions
- Dimensions of Horizontal Gene Transfer in Eukaryotic Microbial Pathogens
- Addressing the Complications of Ebola and Other Viral Hemorrhagic Fever Infections: Using Insights from Bacterial and Fungal Sepsis
- Time for Chocolate: Current Understanding and New Perspectives on Cacao Witches’ Broom Disease Research
- Ganglioside and Non-ganglioside Mediated Host Responses to the Mouse Polyomavirus
- Crosslinking of a Peritrophic Matrix Protein Protects Gut Epithelia from Bacterial Exotoxins
- Structure Elucidation of Coxsackievirus A16 in Complex with GPP3 Informs a Systematic Review of Highly Potent Capsid Binders to Enteroviruses
- CD39 Expression Identifies Terminally Exhausted CD8 T Cells
- Abiotic Stresses Antagonize the Rice Defence Pathway through the Tyrosine-Dephosphorylation of OsMPK6
- Dissociation of Tissue Destruction and Bacterial Expansion during Bubonic Plague
- Interferon-γ: The Jekyll and Hyde of Malaria
- CCR2 Inflammatory Dendritic Cells and Translocation of Antigen by Type III Secretion Are Required for the Exceptionally Large CD8 T Cell Response to the Protective YopE Epitope during Infection
- A New Glycan-Dependent CD4-Binding Site Neutralizing Antibody Exerts Pressure on HIV-1
- The Suramin Derivative NF449 Interacts with the 5-fold Vertex of the Enterovirus A71 Capsid to Prevent Virus Attachment to PSGL-1 and Heparan Sulfate
- Trans-generational Immune Priming Protects the Eggs Only against Gram-Positive Bacteria in the Mealworm Beetle
- Peripheral Vγ9Vδ2 T Cells Are a Novel Reservoir of Latent HIV Infection
- Respiratory Syncytial Virus Disease Is Mediated by Age-Variable IL-33
- TRIM21 Promotes cGAS and RIG-I Sensing of Viral Genomes during Infection by Antibody-Opsonized Virus
- Modeling the Effects of Vorinostat Reveals both Transient and Delayed HIV Transcriptional Activation and Minimal Killing of Latently Infected Cells
- Identification of a Novel Lipoprotein Regulator of Spore Germination
- Calcium Regulation of Hemorrhagic Fever Virus Budding: Mechanistic Implications for Host-Oriented Therapeutic Intervention
- Antigen-Specific Th17 Cells Are Primed by Distinct and Complementary Dendritic Cell Subsets in Oropharyngeal Candidiasis
- Comparative Life Cycle Transcriptomics Revises Genome Annotation and Links a Chromosome Duplication with Parasitism of Vertebrates
- The Autophagy Receptor TAX1BP1 and the Molecular Motor Myosin VI Are Required for Clearance of Salmonella Typhimurium by Autophagy
- Carcinogenic Parasite Secretes Growth Factor That Accelerates Wound Healing and Potentially Promotes Neoplasia
- Effector OspB Activates mTORC1 in a Manner That Depends on IQGAP1 and Promotes Cell Proliferation
- Dengue Virus Infection of Requires a Putative Cysteine Rich Venom Protein
- Distinct Viral and Mutational Spectrum of Endemic Burkitt Lymphoma
- Fundamental Roles of the Golgi-Associated Aspartyl Protease, ASP5, at the Host-Parasite Interface
- Phenotypic and Functional Alterations in Circulating Memory CD8 T Cells with Time after Primary Infection
- Systematic Identification of Cyclic-di-GMP Binding Proteins in Reveals a Novel Class of Cyclic-di-GMP-Binding ATPases Associated with Type II Secretion Systems
- Influenza Transmission in the Mother-Infant Dyad Leads to Severe Disease, Mammary Gland Infection, and Pathogenesis by Regulating Host Responses
- Myeloid Cell Arg1 Inhibits Control of Arthritogenic Alphavirus Infection by Suppressing Antiviral T Cells
- The White-Nose Syndrome Transcriptome: Activation of Anti-fungal Host Responses in Wing Tissue of Hibernating Little Brown Myotis
- Influenza Virus Reassortment Is Enhanced by Semi-infectious Particles but Can Be Suppressed by Defective Interfering Particles
- Identification of the Mechanisms Causing Reversion to Virulence in an Attenuated SARS-CoV for the Design of a Genetically Stable Vaccine
- Differentiation-Dependent KLF4 Expression Promotes Lytic Epstein-Barr Virus Infection in Epithelial Cells
- The Histone Acetyltransferase Hat1 Regulates Stress Resistance and Virulence via Distinct Chromatin Assembly Pathways
- C-di-GMP Regulates Motile to Sessile Transition by Modulating MshA Pili Biogenesis and Near-Surface Motility Behavior in
- Modulation of the Surface Proteome through Multiple Ubiquitylation Pathways in African Trypanosomes
- Crystal Structure of the Human Cytomegalovirus Glycoprotein B
- Depletion of . GlmU from Infected Murine Lungs Effects the Clearance of the Pathogen
- Immunologic Control of Papillomavirus Type 1
- Requires Host Rab1b for Survival in Macrophages
- Structure Analysis Uncovers a Highly Diverse but Structurally Conserved Effector Family in Phytopathogenic Fungi
- PD-L1 Expression on Retrovirus-Infected Cells Mediates Immune Escape from CD8 T Cell Killing
- Phospho-dependent Regulation of SAMHD1 Oligomerisation Couples Catalysis and Restriction
- IL-4 Induced Innate CD8 T Cells Control Persistent Viral Infection
- Crystal Structures of a Piscine Betanodavirus: Mechanisms of Capsid Assembly and Viral Infection
- BCG Skin Infection Triggers IL-1R-MyD88-Dependent Migration of EpCAM CD11b Skin Dendritic cells to Draining Lymph Node During CD4+ T-Cell Priming
- Antigenic Characterization of the HCMV gH/gL/gO and Pentamer Cell Entry Complexes Reveals Binding Sites for Potently Neutralizing Human Antibodies
- Rescue of a Plant Negative-Strand RNA Virus from Cloned cDNA: Insights into Enveloped Plant Virus Movement and Morphogenesis
- Geminivirus Activates to Accelerate Cytoplasmic DCP2-Mediated mRNA Turnover and Weakens RNA Silencing in
- Disruption of Sphingolipid Biosynthesis Blocks Phagocytosis of
- The Fungal Exopolysaccharide Galactosaminogalactan Mediates Virulence by Enhancing Resistance to Neutrophil Extracellular Traps
- The Timing of Stimulation and IL-2 Signaling Regulate Secondary CD8 T Cell Responses
- Structural and Functional Analysis of Murine Polyomavirus Capsid Proteins Establish the Determinants of Ligand Recognition and Pathogenicity
- The Dual Role of an ESCRT-0 Component HGS in HBV Transcription and Naked Capsid Secretion
- PLOS Pathogens
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Chronobiomics: The Biological Clock as a New Principle in Host–Microbial Interactions
- Interferon-γ: The Jekyll and Hyde of Malaria
- Crosslinking of a Peritrophic Matrix Protein Protects Gut Epithelia from Bacterial Exotoxins
- Antigen-Specific Th17 Cells Are Primed by Distinct and Complementary Dendritic Cell Subsets in Oropharyngeal Candidiasis
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání








