-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaSelection against Heteroplasmy Explains the Evolution of Uniparental Inheritance of Mitochondria
Mitochondria contain genes that encode the machinery needed to power cells. Unlike the nuclear genome, the mitochondrial genome is typically inherited from one parent only (uniparental inheritance). The most common explanation for uniparental inheritance is the genomic conflict theory, which states that uniparental inheritance evolved to prevent the spread of ‘selfish’ mitochondria that replicate quickly but produce energy inefficiently. Current explanations have a major problem: when using realistic parameters, mathematical models cannot show that uniparental inheritance can replace biparental inheritance. Clearly, we need a new explanation that fits with standard population-genetic theory. Recent evidence suggests cells may incur a cost when they carry multiple types of mitochondria. Here we show mathematically that uniparental inheritance could have evolved to avoid the costs of maintaining multiple mitochondrial lineages within a cell. Our results explain the long-standing evolutionary mystery of uniparental inheritance and provide insight into the evolution of mating types and binary sexes. Selection against heteroplasmy also has implications for the evolution of the mitochondrial genome because new mitochondrial haplotypes always lead to heteroplasmy before becoming fixed in the population. Thus, selection against heteroplasmy may explain why mtDNA coding-genes have slower substitution rates than analogous genes within the nucleus.
Published in the journal: . PLoS Genet 11(4): e32767. doi:10.1371/journal.pgen.1005112
Category: Research Article
doi: https://doi.org/10.1371/journal.pgen.1005112Summary
Mitochondria contain genes that encode the machinery needed to power cells. Unlike the nuclear genome, the mitochondrial genome is typically inherited from one parent only (uniparental inheritance). The most common explanation for uniparental inheritance is the genomic conflict theory, which states that uniparental inheritance evolved to prevent the spread of ‘selfish’ mitochondria that replicate quickly but produce energy inefficiently. Current explanations have a major problem: when using realistic parameters, mathematical models cannot show that uniparental inheritance can replace biparental inheritance. Clearly, we need a new explanation that fits with standard population-genetic theory. Recent evidence suggests cells may incur a cost when they carry multiple types of mitochondria. Here we show mathematically that uniparental inheritance could have evolved to avoid the costs of maintaining multiple mitochondrial lineages within a cell. Our results explain the long-standing evolutionary mystery of uniparental inheritance and provide insight into the evolution of mating types and binary sexes. Selection against heteroplasmy also has implications for the evolution of the mitochondrial genome because new mitochondrial haplotypes always lead to heteroplasmy before becoming fixed in the population. Thus, selection against heteroplasmy may explain why mtDNA coding-genes have slower substitution rates than analogous genes within the nucleus.
Introduction
During sexual reproduction, offspring receive two genomes: nuclear genomes from both parents and haploid cytoplasmic genomes, contained in mitochondria and chloroplasts (in plants and algae), usually from one parent. Although uniparental inheritance is nearly ubiquitous, the reasons behind its evolution remain unresolved [1, 2]. Cells contain multiple mitochondria, and the mitochondrial genome (mtDNA) encodes polypeptide subunits of the electron transport chain, which the cell uses to generate ATP via oxidative phosphorylation [2]. If mutations increase mtDNA replication rate but simultaneously decrease respiration, then increased mtDNA fitness comes at the expense of cell and organism fitness [3–5]. Nuclear and mitochondrial genomes are thus potentially in conflict. The genomic (or selfish) conflict theory argues that uniparental inheritance evolved because biparental inheritance facilitates the spread of such selfish mitochondria [1, 3–6]. Although the conflict theory has been the predominant explanation for uniparental inheritance for over three decades [3, 4], other explanations exist. A second theory suggests that uniparental inheritance facilitates the removal of deleterious mutations. Uniparental inheritance decreases variation of mtDNA within cells, but increases variation between cells, allowing purifying selection against cells with increased mutation load [1, 7]. A third hypothesis argues that because the oxidative phosphorylation pathway is composed of interacting nuclear - and mitochondrial-encoded polypeptides, uniparental inheritance optimizes mitochondrial-nuclear coadaptation by maintaining coevolved mitochondrial-nuclear combinations [1, 8]. While uniparental inheritance spreads in mathematical models of the above hypotheses [1, 5, 6], it cannot replace biparental inheritance under realistic assumptions and parameter values [1, 5]. Thus, despite decades of theoretical work, we still lack a convincing explanation for why uniparental inheritance is widespread amongst extant organisms [1, 2].
Although uniparental inheritance is the general rule in eukaryotes, there are a few exceptions. Probably the best-known exception is baker’s yeast (Saccharomyces cerevisiae) in which both parents contribute mitochondria to offspring [9, 10]. However, the repeated division of cells that contain two mitochondrial lineages (heteroplasmy) leads to cells that contain a single type of mitochondria (homoplasmy) [9, 10]. Another example is the male bivalve (Mytilus), which also inherits mitochondria from both parents. But in this case maternal and paternal mitochondria do not mix within single cells, as maternal mitochondria segregate to the soma while paternal mitochondria segregate to the gonads [11]. Thus, even when mitochondria are inherited from both parents, heteroplasmy is avoided. Recent experimental evidence suggests that this is because heteroplasmy imposes a cost on the organism. A study on mice found that the mere mixing of different, but phenotypically normal, mitochondria within a cell leads to physiological and behavioral abnormalities [12]. Could uniparental inheritance have evolved simply because carrying multiple mitochondrial types imposes a cost on the organism? Here we use a mathematical model to explore whether selection against heteroplasmy could have led to the evolution of uniparental inheritance.
Basic model description
Our model is based on an idealized life cycle of a single-cell diploid eukaryotic organism, such as the algae Chlamydomonas reinhardtii. Diploid cells contain n mitochondria and haploid cells have n/2 mitochondria. All mitochondria are initially wild type but mitochondria can mutate from wild type to mutant (and vice versa). The starting population contains haploid gametes with a nuclear allele regulating biparental inheritance (B). Gametes are evenly split between two nuclear self-incompatible mating types (B1 and B2). In the basic model, we assume no recombination between the mitochondrial inheritance and mating type loci because these are tightly linked in many isogamous organisms [9] (later we explore recombination and no mating types). Cell types are characterized by the proportion of wild type and mutant mitochondria that they carry and their nuclear allele (haploid) or genotype (diploid).
Our life cycle has four discrete stages and is similar to the life cycles used in previous models [1, 5, 8]. Since we begin with a population of gametes, the first stage is random mating. Here, gametes randomly mate with the opposite mating type to produce diploid cells. Matings are controlled by the nuclear allele in gametes. In biparental inheritance (between B1 and B2 gametes), both gametes contribute mitochondria to the B1B2 diploid cells (see later for uniparental inheritance). The second stage is mutation. Each mitochondrion can mutate to the other haplotype with probability μ. The third stage is selection. Here, diploid cells have a relative fitness based on the proportion of each haplotype in the cell. We assume that fitness decreases as the level of heteroplasmy increases. The fourth stage is meiosis, where diploid cells produce gametes that contain a single nuclear allele and n/2 mitochondria. As mitochondria are stochastically partitioned into gametes [9], diploid heteroplasmic cells produce gametes with varying degrees of heteroplasmy.
First, we let the population of B1 and B2 gametes reach mutation-selection equilibrium. We then simulate a mutation leading to uniparental inheritance of mitochondria by converting a small proportion (10−2) of B1 gametes to U1 gametes. We assume no further mutations between B and U alleles. Matings between U1 and B2 gametes result in uniparental inheritance, in which the U1B2 cell inherits mitochondria from U1 alone. (Matings between U1 and B1 are not possible as they are the same mating type.) The population now consists of three alleles (U1, B1 and B2) and two genotypes (U1B2 and B1B2). The model tracks the proportion of each cell type at each stage of the life cycle. U1 spreads at the expense of B1 when uniparental inheritance is more advantageous than biparental inheritance (the frequency of B2 always remains at 0.5), and the simulation ends when the alleles reach equilibrium (see Model and S1–S6 Model for details of the model).
To explore whether a cost to heteroplasmy could have led to the evolution of uniparental inheritance, we study several scenarios. We first examine the simplest case, where mutations in mitochondria are neither advantageous nor disadvantageous (neutral mutations), but heteroplasmic cells incur a fitness cost proportional to the degree of heteroplasmy. Because no empirical data relate fitness to the degree of heteroplasmy, we consider three forms of fitness function to describe selection against heteroplasmy: concave, linear and convex (Fig 1A). For each fitness function, we vary the cost of heteroplasmy (ch), given by ch = 1 − h where h is the fitness of the most heteroplasmic cell in the population, to see how this affects the spread of U1. We generate the concave fitness function by
the linear function by and the convex function byFig. 1. Uniparental inheritance replaces biparental inheritance for all tested parameter values. 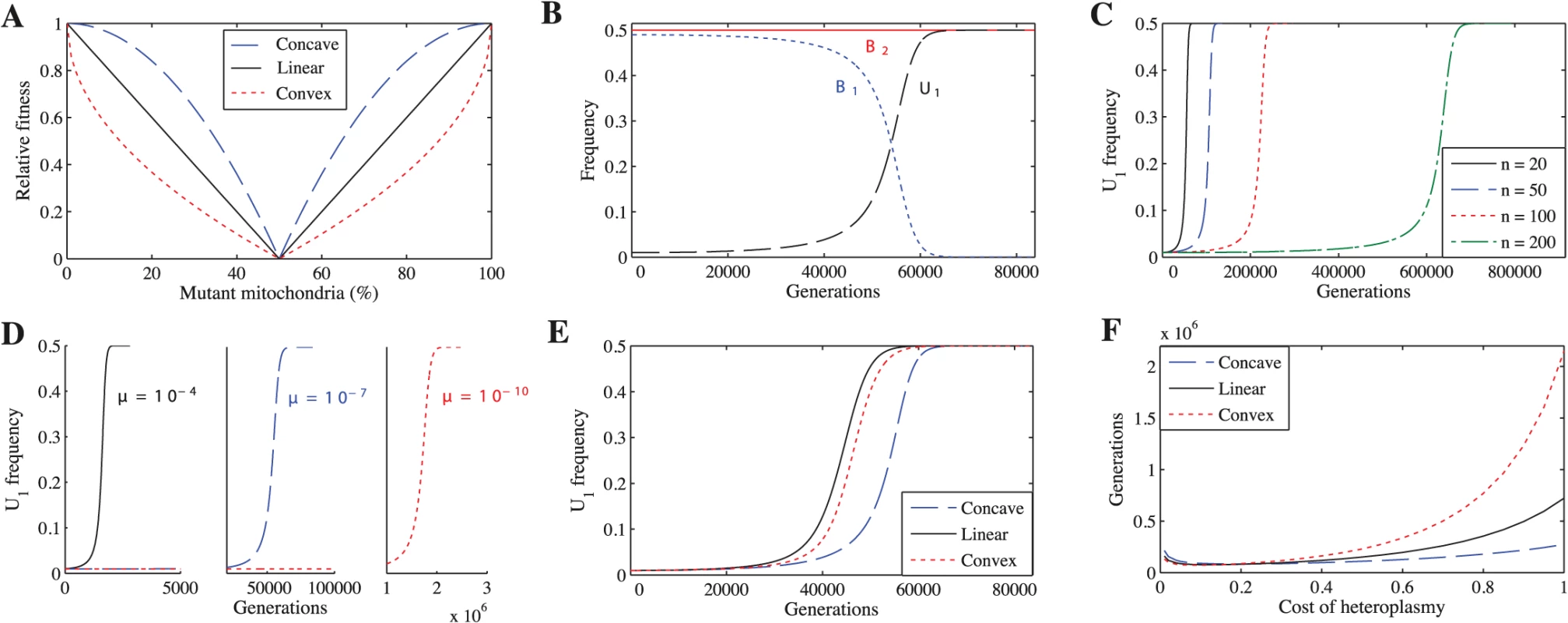
(A) The three fitness functions when ch = 1. Unless indicated otherwise, the parameters for B-F are n = 20, μ = 10−7, ch = 0.2 and concave fitness. (B) U1 replaces B1. (C) U1 takes longer to replace B1 as n increases. (D) U1 takes longer to replace B1 as μ decreases. (E) U1 replaces B1 under all three fitness functions. (F) Number of generations for U1 to replace B1 across a range of costs of heteroplasmy. U1 replaces B1 even if the cost of heteroplasmy is extremely low. We also vary μ (mutation rate) and n (number of mitochondria) to ensure that our findings are robust. Second, we explore the effect of advantageous or deleterious mutations (non-neutral mutations) on the spread of U1. Third, we relax the assumption of tight linkage between mating type and inheritance loci by exploring two cases: recombination between mating types and the absence of mating types altogether. Finally, we examine whether selection against heteroplasmy can explain the rare, but nevertheless important, exceptions to uniparental inheritance. To ensure that our results generalize to more than two mitochondrial types, we developed a second model that considers three mitochondrial types (S6 Model).
Results
When both mitochondrial haplotypes are neutral
We find that U1 always replaces B1, resulting in complete uniparental inheritance in the population (Fig 1B). These findings are independent of the number of mitochondria per cell (Fig 1C), mutation rate (Fig 1D), fitness function (Fig 1E), and cost of heteroplasmy (Fig 1F) (see S1–S10 Tables for more parameter combinations). We find the same results when we generalize the model to three mitochondrial haplotypes (S1 Fig).
General patterns
In our model, heteroplasmic cells are generated by mutation. During meiosis, heteroplasmic cells produce gametes with varying levels of heteroplasmy, including homoplasmic gametes. Uniparental inheritance maintains this variation created by meiosis, which leads to homoplasmic U1B2 cells (Fig 2A–2B and S2A–S2B Fig). Mutants that arise in U1B2 cells quickly segregate into U1 gametes that carry mutant haplotypes only (Fig 3A–3B and S3A–S3B Fig), which leads to U1B2 cells that are homoplasmic for mutant mitochondria (Fig 2B and S2B Fig). Since we assume that mutations are neutral, cells homoplasmic for mutant mitochondria suffer no fitness costs.
Fig. 2. Fitness and distribution of cell types. 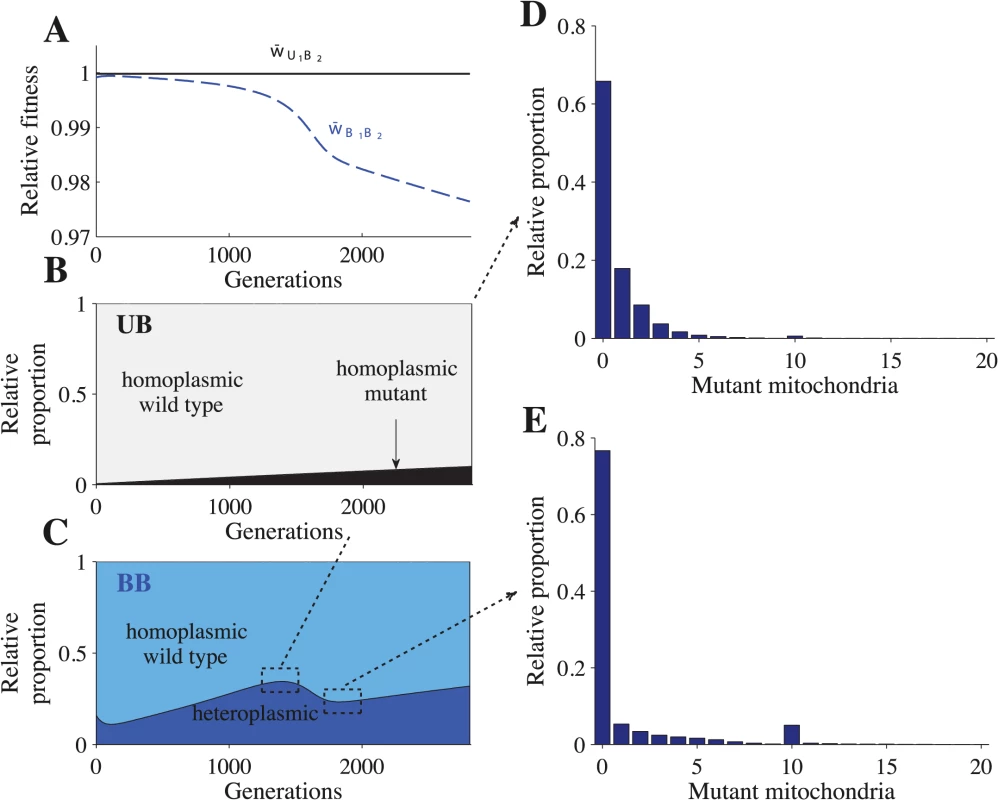
Parameters: n = 20, μ = 10−4, ch = 0.2 and concave fitness. U1B2 cells appear at generation 0, which is the point at which the B1 and B2 gametes reach mutation-selection equilibrium. (A) Relative advantage of each genotype through time (see Model for details). For B-E, the relative proportion is the sum of a particular cell type divided by the sum of all cells that carry the same genotype. The heteroplasmic category includes all cells with any level of heteroplasmy. B-C shows the distribution of cells carrying the U1B2 genotype (B) and the B1B2 genotype (C). D-E show a more detailed distribution of cell types carrying the B1B2 genotype at generation 1350 (D) and at generation 1820 (E). The decrease in heteroplasmy in B1B2 cells between generations 0–100 is an artifact of introducing U1 at a frequency of 0.01 (the influx of U1 gametes homoplasmic for the wild type haplotype converts some heteroplasmic B1 and B2 gametes into homoplasmic gametes, which increases the proportion of homoplasmic B1B2 cells). From generations 1350–1820, the proportion of heteroplasmic B1B2 cells decreases (C) but the level of heteroplasmy increases (compare D with E). This more than offsets the decrease in the proportion of heteroplasmic cells and w¯B1B2 continues to decrease (A). Fig. 3. Fitness and distribution of gamete types. 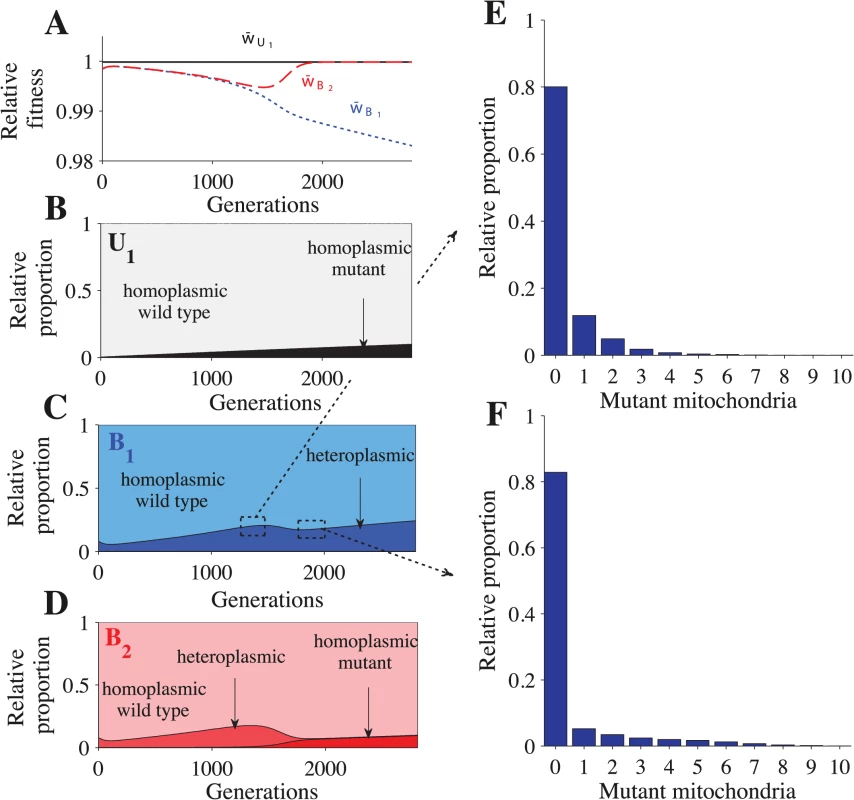
Parameters: n = 20, μ = 10−4, ch = 0.2 and concave fitness. U1 gametes appear at generation 0, which is the point at which the B1 and B2 gametes reach mutation-selection equilibrium. (A) Relative advantage of each gamete through time (see Model for details). For B-F, the relative proportion is the sum of a particular gamete type (e.g. a homoplasmic wild type U1 gamete) divided by the sum of all cells carrying that allele (all gametes carrying the U1 allele). Thus, the relative proportion describes how an allele is distributed across different gamete types but it does not show their actual frequencies in the population. The heteroplasmic category combines all gametes with any level of heteroplasmy. B-D show the distribution of gametes carrying the U1 allele (B), B1 allele (C) and the B2 allele (D). E-F show a more detailed distribution of gametes carrying the B1 allele at generation 1350 (E) and generation 1820 (F). The decrease in heteroplasmy in B1 and B2 gametes between generations 0–100 is an artifact of introducing U1 at a frequency of 0.01 (the influx of U1 gametes homoplasmic for the wild type haplotype converts some heteroplasmic B1 and B2 gametes into homoplasmic gametes). From generations 1350–1820, the proportion of heteroplasmic B1 and B2 gametes decreases (C and D) but the level of heteroplasmy increases (compare E with F). This more than offsets the decrease in the proportion of heteroplasmic cells and w¯B1 continues to decrease (A). Around generation 1350, B2 gametes homoplasmic for mutant mitochondria begin to appear, which causes w¯B2 to increase and eventually converge with w¯U1. U1B2 cells carrying mutant mitochondria produce B2 gametes that also carry mutant mitochondria (Fig 3D and S3D Fig). When these B2 gametes mate with B1 gametes carrying wild type mitochondria, the resulting B1B2 cells are highly heteroplasmic (Fig 2C–2E and S2C Fig). As U1 spreads, matings between U1 and B2 become more likely, increasing the level of heteroplasmy in both B1B2 cells and in B1 and B2 gametes (Figs. 2C–2E and 3C–3F and S2C and S3C–S3D Figs.). Increased levels of heteroplasmy reduce the fitness of both B1 and B2 gametes (w¯B1, w¯B2 in Fig 3A and S3A Fig) and B1B2 cells (w¯B1B2 in Fig 2A and S2A Fig). The difference in fitness between B1 and B2 becomes stronger (Fig 3A and S3A Fig) as more B2 gametes that carry mutant mitochondria are produced (Fig 3D and S3D Fig). As a result U1 spreads at the expense of B1.
In the above description (Figs. 2 and 3), the mutation from B1 to U1 occurred in gametes homoplasmic for wild type mitochondria. When U1 is introduced into heteroplasmic gametes, it takes fewer generations to reach equilibrium because B2 gametes homoplasmic for mutant mitochondria are produced more quickly (S4 Fig). Our results are robust to changes in the frequency at which U1 gametes are introduced (S5 Fig). For more detailed model dynamics, see S1 Text and S1–S2 Videos.
The effect of varying parameters
U1 spreads more slowly when mutation rate (μ) is lower (Fig 1D) and number of mitochondria (n) is higher (Fig 1C). Reducing μ slows the spread of U1 because mutant mitochondria are produced more slowly, slowing the generation of B2 gametes that only carry the mutant haplotype. Increasing n has the same effect.
While varying the cost of heteroplasmy does not change the qualitative behavior of the model, it does affect the number of generations required for U1 to replace B1 (Fig 1F). In general, U1 spreads more quickly when the cost of heteroplasmy is low for all three fitness functions (Fig 1F). Strong selection against heteroplasmy (e.g. ch = 1) slows the production of B2 gametes homoplasmic for the mutant haplotype because a transition via heteroplasmy is needed to lead to U1B2 cells homoplasmic for mutant mitochondria. Heteroplasmy levels thus remain low in B1B2 cells, and U1 takes longer to replace B1 (S6A and S6D Fig). At lower costs of heteroplasmy (e.g. ch = 0.2), more B2 gametes that are homoplasmic for the mutant haplotype are produced and levels of heteroplasmy in B1B2 cells increase, leading to a faster spread of U1 (S6B and S6E Fig). Although levels of heteroplasmy in B1B2 cells increase even further as the cost of heteroplasmy approaches 0 (e.g. ch = 0.01), selection against heteroplasmy is now very weak, which slows the spread of U1 compared with ch = 0.2 (S6C and S6F Fig). When the number of mitochondria is higher, U1 spreads more quickly when the cost of heteroplasmy is low. This is because B2 gametes homoplasmic for mutant mitochondria are produced more slowly at higher values of n and strong selection against heteroplasmy compounds this problem (S7 Fig). A similar logic can be applied to understand the differences between the three fitness functions. Since heteroplasmic cells are under weaker selection when fitness is concave (followed by linear and convex respectively) (Fig 1A), the level of heteroplasmy is highest using a concave function (S8 Fig). Thus, U1 spreads more quickly using a concave function (followed by linear and convex respectively) when the cost of heteroplasmy is high because it is easier to generate heteroplasmic cells, and thus easier to generate B2 gametes homoplasmic for mutant mitochondria, when selection against heteroplasmic cells is weaker (Fig 1F and S8 Fig). As the cost of heteroplasmy decreases, the number of generations for U1 to spread under the three fitness functions converges because it becomes easier to generate B2 gametes homoplasmic for mutant mitochondria (Fig 1F).
When mutations are deleterious
We next investigate how the U1 allele spreads when mutations are non-neutral, as is the case for most mtDNA mutations [13]. We start by assuming that mutations are deleterious so that cells carrying mutant mitochondria are more strongly selected against than cells that carry wild type mitochondria. We assume that a mutation from wild type to mutant haplotype is more common than the reverse [14]. We let the probability of a mutation from mutant to wild type haplotype be μb = μ/100. We vary the selection coefficient of the mutant haplotype to see how this affects the spread of the U1 allele (the fitness of a cell homoplasmic for the mutant haplotype is 1 − sd, where sd is the selection coefficient of the mutant haplotype). Essentially there are now two fitness functions: one governing the effect of mitochondria on cell fitness (where the selection coefficient determines the magnitude of the effect) and one governing the cost of heteroplasmy. For deleterious mutations, we assume that fitness decreases as a concave function of the number of mutants, as this relationship is experimentally established [15]. We examine both concave and convex fitness functions for selection against heteroplasmy (yielding two combinations).
Again, U1 replaces B1 unless the fitness of heteroplasmic cells and the fitness of deleterious mutants are governed by a concave function and the selection coefficient is sufficiently large (S9 Fig and S11–S12 Tables). U1 generally spreads more slowly as sd increases and it always spreads more slowly compared to when mutations are neutral (S11–S12 Tables). Stronger selection against mutant haplotypes leads to fewer B2 gametes homoplasmic for mutant mitochondria, which slows the spread of U1 (S10 Fig).
When mutations are advantageous
Next we explore the effect of advantageous mutations on the spread of U1. In this case, cells that carry mutant haplotypes have an advantage over those carrying wild type haplotypes (the fitness of a cell homoplasmic for the wild type haplotype is 1 − sa, where sa is the selection coefficient of the mutant haplotype). We account for the rarity of advantageous mutations by setting μb = 100μ. Because it is unknown how fitness relates to the accumulation of advantageous mtDNA mutations, we model this relationship with both a concave and convex function. As in the deleterious case, we model selection against heteroplasmy by testing both concave and convex fitness functions (giving four combinations).
U1 always replaces B1 unless mutations are highly advantageous (sa = 0.1) and both the fitness of heteroplasmic cells and the fitness of advantageous mutants are governed by a concave function (S9 Fig and S13–S14 Tables). U1 spreads more quickly when sa = 0.001 and sa = 0.01 because B2 gametes homoplasmic for mutant haplotypes now have a fitness advantage and are produced more quickly (S10 Fig). In contrast, U1 spreads more slowly when sa = 0.1 because the mutant haplotype quickly replaces the wild type as the dominant haplotype before U1 has replaced B1. Once B1 gametes carry mostly mutant haplotypes, B1 × B2 matings are less costly because they predominantly involve mutant haplotypes. We find the same patterns for non-neutral mutations when we generalize our model to three mitochondrial types (S15 Table).
Recombination between mating type and inheritance loci
Previously, U × U matings were not possible because we assumed tight linkage between mating type and inheritance loci. But if we allow recombination to occur between these loci, U1 × U2 matings become possible. In this scenario, the number of gametes increases to four (B1, B2, U1 and U2), as does the number of genotypes (B1B2, U1B2, U1U2 and U2B1). There are three main ways in which mitochondrial inheritance could be regulated in U1 × U2 matings. (1) One U allele is dominant to the other, leading to uniparental inheritance; (2) each U allele ensures inheritance of its mitochondria, resulting in biparental inheritance; or (3) inheritance is more or less random so that some matings result in uniparental inheritance and some in biparental inheritance. We model all three cases.
When U1 × U2 matings lead to uniparental inheritance, the U1U2 genotype always spreads until it is fixed in the population, leading to complete uniparental inheritance (Fig 4A and S16–S18 Tables). When U1 × U2 matings lead to biparental inheritance, however, uniparental inheritance does not become fixed and the population reaches a polymorphic equilibrium (Fig 4B–4C). Under these conditions, the frequency of uniparental inheritance at equilibrium is ≤ 0.5 (S19–S21 Tables). Uniparental inheritance cannot exceed 0.5 because increasing the frequency of U1 or U2 simply increases the proportion of biparental U1 × U2 matings. The frequency of uniparental inheritance remains very low when we assume a concave fitness function (Fig 4B), but reaches its maximum (0.5) when we assume a linear or convex fitness function (Fig 4C) (see S12–S13 Figs. for an explanation).
Fig. 4. Recombination and no mating types scenarios. 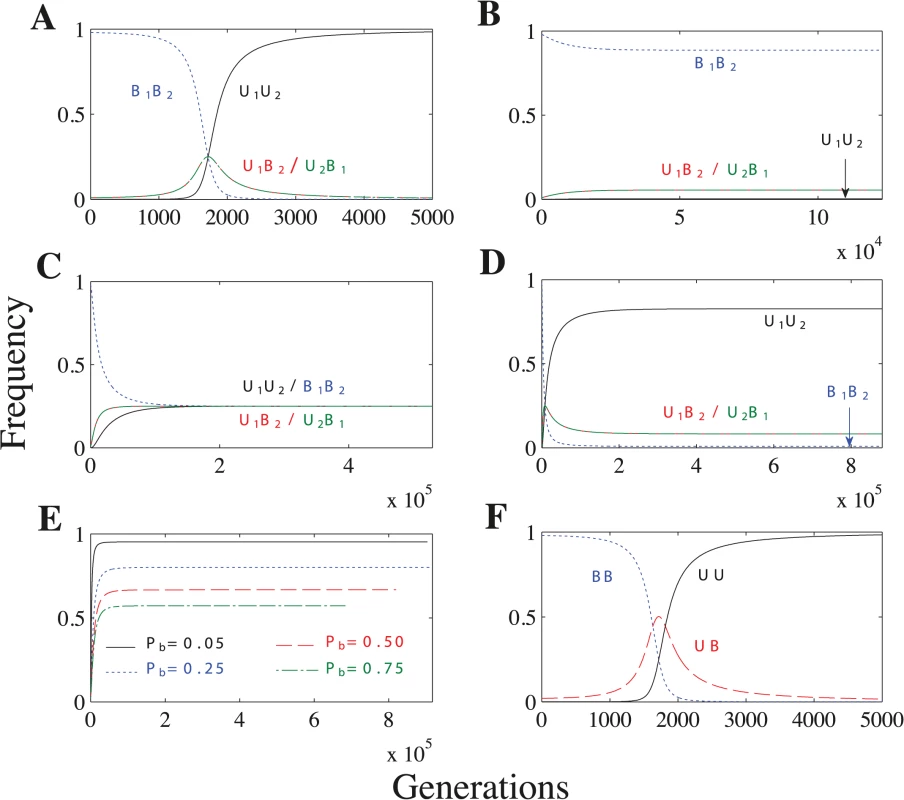
Parameters: n = 20, μ = 10−4, ch = 0.2. (A) As the U allele initially spreads (generations 0–1700), the U1B2/U2B1 genotypes increase in frequency. But, because U1B2 and U2B1 cells lead to B1B2 cells through meiosis and random mating, the U1U2 genotype soon takes over and uniparental inheritance becomes fixed. Additional parameters: Pr = 0.5 and concave fitness. (B) Biparental inheritance dominates when U × U matings are biparental and fitness is concave. (C) Uniparental inheritance invades to its maximum value (0.5) when U × U matings are biparental and fitness is linear or convex. (The frequency of uniparental inheritance is the sum of U1U2 and U2B1.) Additional parameters: linear fitness. (D) U × U matings have a mixture of uniparental and biparental inheritance. Unlike in B, U1U2 no longer becomes fixed because some U × U matings now have biparental inheritance and further increasing U1U2 would only increase the overall level of biparental inheritance. Additional parameters: Pb = 0.1 and linear fitness. (E) Lines represent the frequency of uniparental inheritance in separate simulations with linear fitness and varying probabilities of biparental inheritance (Pb) when U × U matings have a mixture of uniparental and biparental inheritance. As Pb increases, U × U matings are more likely to lead to biparental inheritance, which decreases the frequency of uniparental inheritance at equilibrium. (F) No mating types scenario under concave fitness. F is identical to A except that the frequency of UB in F is the sum of the U1B2 and U2B1 freqencies in A. When the probability of recombination (Pr) is sufficiently high (10−4 ≤ Pr ≤ 0.5 in S11 Fig), the U1B2 and U2B1 genotypes have the same frequency at equilibrium (S11B–S11D Fig). Now uniparental inheritance is no longer associated with a single mating type but is evenly split between the two mating types (S19–S21 Tables). When Pr is sufficiently small (Pr = 10−5 in S11 Fig), the recombination rate is so low that the mating type and inheritance loci are essentially linked and the U1B2 genotype becomes fixed (as in the general model) (S11A Fig).
When we assume a mixture of uniparental inheritance and biparental inheritance, we let U1 × U2 matings lead to biparental inheritance with probability Pb and to uniparental inheritance with probability 1 − Pb. Lowering Pb increases the frequency of uniparental inheritance, and uniparental inheritance becomes fixed when Pb = 0 (Fig 4A and 4E). Under linear and convex fitness functions, the equilibrium always maximizes the level of uniparental inheritance (Tables S22–S23). Under concave fitness, however, uniparental inheritance is only maximized for particular values of Pb (roughly Pb ≤ 0.2 for the parameter values we considered) (S22 Table; rows 2–3). (See S5 Model for how we determine when uniparental inheritance is maximized.)
We also find that uniparental inheritance can evolve in the complete absence of mating types. The no mating types scenario differs from the recombination case in that UB equals the sum of U1B2 and U2B1 at equilibrium (Fig 4A and 4F) (see S2 Text for more details).
Can selection against heteroplasmy explain the exceptions to uniparental inheritance?
In this section, we explore whether relaxing some of the assumptions in our general model can lead to mitochondrial inheritance patterns that resemble some of the known exceptions to uniparental inheritance. Exceptions to uniparental inheritance fall in three main categories: organisms that (1) regularly inherit mitochondria from both parents; (2) normally inherit mitochondria from one of the two parents but on occasion inherit mitochondria from both; and (3) inherit mitochondria from either or both parents.
Baker’s yeast, Saccharomyces cerevisiae, regularly inherits mitochondria from both parents (though uniparental inheritance also occurs), but heteroplasmy is transient because the diploid cell has only a few mitochondria [16] and divides repeatedly, which separates heteroplasmic cells into cells homoplasmic for either mitochondrial type (vegetative segregation) [9, 10]. Vegetative segregation is usually completed within twenty generations, but up to 50% of zygotes may be homoplasmic after the first division ([10] and references therein). Thus, Saccharomyces may restore homoplasmy as quickly as organisms that actively destroy one mitochondrial lineage [17]. Similarly, the geranium Pelargonium zonale often inherits cytoplasmic organelles from both parents (chloroplasts in this case). As with Saccharomyces, heteroplasmy is transient in Pelargonium because of rapid vegetative segregation of heteroplasmic cells shortly after syngamy [9]. We added mitotic divisions to our model to test whether vegetative segregation could maintain biparental inheritance under selection against heteroplasmy. When we include mitosis before selection (which assumes that vegetative segregation occurs swiftly, before selection has time to act), uniparental inheritance does not spread, provided that the number of mitochondria is low (n = 4) and the number of divisions is high (S24 Table; rows 7–8). Under these conditions, biparental inheritance is stable because heteroplasmic cells resulting from biparental inheritance segregate into homoplasmic cells before selection acts. If there are insufficient mitotic divisions, or if selection acts before vegetative segregation is complete, then uniparental inheritance replaces biparental inheritance, although it spreads much more slowly than when there are no mitotic divisions (S24 (rows 3–6) and S25 Tables). When there are more mitochondria per cell (e.g. n = 8), biparental inheritance is only stable if the number of cell divisions increases to compensate (S24 Tables; rows 9–10). Thus, biparental inheritance can be stable under selection against heteroplasmy but only under a narrow set of conditions, explaining why this form of inheritance is rare.
In other isogamous organisms, including the acellular slime molds Physarum polycephalum and Didymium iridis and the algae Chlamydomonas reinhardtii, mitochondria from both gametes mix before one mitochondrial lineage is destroyed post-fertilization, often by nucleases [18–20]. This mechanism is not perfect and these organisms sometimes deviate from strict uniparental inheritance [9, 18–20]. While uniparental inheritance is the norm in the slime mold P. polycephalum, sometimes both mitochondrial lineages survive, leading to varying degrees of biparental inheritance [18]. Could uniparental inheritance still spread under such conditions? Since mating types and inheritance loci are tightly linked in Physarum [18], we explore this question using our general model that assumes linkage. Now, U1 × B2 matings lead to biparental inheritance with probability Pb and to uniparental inheritance with probability 1 − Pb. For the parameter values that we examined, the U1B2 genotype always goes to fixation when Pb < 1 and the fitness function is linear or convex (S26 Table). (When fitness is concave, Pb must be roughly <0.05 for the U1B2 genotype to become fixed.) Under these conditions, the frequency of biparental inheritance at equilibrium is equal to Pb (S26 Table). In this scenario, the level of biparental inheritance in the population simply reflects the likelihood that an individual mating results in biparental inheritance.
Chlamydomonas reinhardtii and Didymium iridis can inherit mitochondria from either or both parents [19, 20]. Chlamydomonas normally inherits mitochondria from the mt − parent and chloroplasts from the mt + parent, but under some circumstances it can inherit mitochondria from mt + and chloroplasts from mt − or mitochondria and chloroplasts from both [20]. Didymium iridis has random, biased, or dominant patterns of uniparental inheritance. Under random uniparental inheritance, either parental strain is equally likely to be the mitochondrial donor while, under biased inheritance, one strain is more likely to be the mitochondrial donor [19]. Under dominant inheritance, one strain is always the donor. Didymium also has low levels of biparental inheritance [19]. In this scenario, we test whether selection against heteroplasmy could lead to the evolution of a system with a mixture of uniparental inheritance (from either parent) and biparental inheritance. We assume that mating types can recombine and that U1 × U2 matings can lead to mitochondria being inherited from U1, U2 or both. Mitochondria are inherited from U1 with probability PU1, from U2 with probability PU2 and from both parents with probability Pb (where PU1+PU2+Pb=1). Now, uniparental inheritance comes from U1 × B2 matings, U2 × B1 matings and those U1×U2 matings with uniparental inheritance. Irrespective of the values of PU1 and PU2, we find the same results as with our earlier model in which U1×U2 matings led to a mixture of uniparental and biparental inheritance (S22–S23 Tables). This is because equilibrium depends only on the value of Pb. (Since uniparental inheritance quickly eliminates most heteroplasmic cells, U1U2 cells are almost entirely homoplasmic regardless of which gamete donates mitochondria.) Consequently, different probabilities of inheriting mitochondria biparentally (Pb), from mating type 1 (PU1) or from mating type 2 (PU2) lead to a range of inheritance patterns that include uniparental inheritance (from both parents) and biparental inheritance (see S27 Table for some examples).
Lastly, selection against heteroplasmy provides an explanation for the cases in which mitochondria are inherited from one parent while chloroplasts are inherited from the other (e.g. in Chlamydomonas and pines [20, 21]). If uniparental inheritance simply evolved to maintain homoplasmy in cells, it should not matter which parent donates mitochondria or chloroplasts.
Discussion
Our model shows that selection against heteroplasmy can lead to the fixation of uniparental inheritance in an ancestrally biparental population. We find that uniparental inheritance replaces biparental inheritance under almost all tested scenarios and parameter values. Our model also explains many of the known exceptions to strict uniparental inheritance. We show that uniparental inheritance can replace biparental inheritance whether mutations lead to neutral or non-neutral haplotypes. Relaxing our initial assumptions of pre-existing mating types and lack of recombination does not prevent uniparental inheritance from evolving. As we make no attempt to resolve the evolution of mating types within the context of mitochondrial inheritance, as others have previously attempted [1, 22], our findings thus leave open the possibility that mating types preceded uniparental inheritance, evolved as a consequence of uniparental inheritance, or evolved after uniparental inheritance.
In contrast to previous models, we show that uniparental inheritance can spread under realistic mutation rates and number of mitochondria per cell. The lowest value of μ that we tested (10−10) is eight orders of magnitude lower than required by the genomic conflict theory [1] and compares favorably with empirical mutation rates (10−7 to 10−8 per site per generation [23–25]). Both the genomic conflict and mutation clearance hypotheses require unrealistic mutation rates and number of mitochondria per cell for uniparental inheritance to replace biparental inheritance, while uniparental inheritance cannot replace biparental inheritance under any parameter values in the mitochondrial-nuclear coadaptation model [1]. The genomic conflict model requires a mutation rate of 1% per generation before uniparental inheritance can replace biparental inheritance [1]. The only known example that satisfies this assumption is the petite mutant in Saccharomyces cerevisiae, which is a hyper-mutable selfish mitochondrion that can spontaneously arise at a rate of 1% per generation [26]. Under this mutation rate, however, the genomic conflict model requires that cells contain at least 50 mitochondria [1], whereas most extant isogamous species, including Saccharomyces, contain fewer than 20 mitochondria at syngamy [16, 18]. As mutant mitochondria lack a transmission advantage over wild type mitochondria in the mutation clearance hypothesis, the mutation clearance model requires even higher mutation rates [1]. To the best of our knowledge, no extant organism satisfies the assumptions of the genomic conflict or mutation clearance hypotheses.
Why do our results differ from the findings of previous models? In the genomic conflict and mutation clearance models, wild type mitochondria mutate to selfish or deleterious mitochondria. Biparental inheritance results in cells that are heteroplasmic for wild type and mutant mtDNA, while U1 gametes mostly contain wild type mitochondria [1]. Because U1 purges B2 gametes of mutant mitochondria, B1×B2 matings involve increasingly fewer mutant mitochondria as the frequency of U1 increases [1, 5]. U1 is thus subject to negative frequency-dependent selection, and the population reaches equilibrium well before uniparental inheritance replaces biparental inheritance at realistic mutation rates [1]. The mitochondrial-nuclear coadaptation model assumes that mitochondria are well matched or poorly matched to nuclear alleles [1, 8]. Because mutation can lead to matched nuclear-mitochondrial states becoming unmatched, the effective mitochondrial mutation rate is lower in the mitochondrial-nuclear coadaptation model, which prevents uniparental inheritance from displacing biparental inheritance under any parameter values [1].
Evidence for a cost of heteroplasmy comes from a recent study that compared the effect of two mtDNA haplotypes (NZB and 129S6) in a cogenic nuclear background on the functioning of mice [12]. Mice homoplasmic for NZB or 129S6 were phenotypically normal, but NZB-129S6 heteroplasmic mice suffered from reduced activity, lowered food intake, compromised respiration, heightened stress response, and impaired cognition [12]. While the mechanism(s) behind the cost of heteroplasmy is unknown, there are a few possibilities. Heteroplasmy may disrupt cell signaling by altering production of reactive oxygen species (ROS) [27] and there are indications that heteroplasmy can increase mitochondrial ROS levels [28, 29], leading to phenotypes that differ from cells that are homoplasmic for either haplotype [29, 30]. Alternatively heteroplasmy may lead to deleterious interactions between polypeptides from different mitochondria within the same electron transport chain [12, 31]. Because chloroplasts also contain independent genomes, are involved in cellular bioenergetics, and generally show uniparental inheritance [9], our findings likely apply to both mitochondria and chloroplasts.
Although the evidence in mice is compelling [12], it is unknown whether selection against heteroplasmy is a general phenomenon in eukaryotes. While Sharpley and colleagues [12] used different mitochondrial lineages to construct heteroplasmic individuals, our model assumes that mutations accumulated within a single generation can cause mitochondrial types to become sufficiently distinct to lead to negative effects for the cell. At this stage we do not know how different mitochondrial genomes have to be for selection against heteroplasmy to apply. It could also be that there are regions of the genome in which heteroplasmic mutations have a stronger effect on fitness than others. To support or refute our model, we now need solid empirical data on a range of organisms showing the cost, if any, of heteroplasmy on organism fitness.
While we have referred to n as the number of mitochondria in the cell, n actually refers to the number of segregating units of mtDNA at syngamy. Mitochondria pack DNA into DNA-protein complexes called nucleoids, which themselves may contain multiple copies of mtDNA [32, 33]. It is currently unknown whether the segregating unit is the mtDNA molecule itself, the nucleoid, the mitochondrion or another level of mtDNA organization [33]. But as nucleoids are predominantly homoplasmic, even in heteroplasmic tissues [32, 33], the number of mitochondria may be a reasonable approximation of the number of segregating units in the cell. If the segregating unit is at a lower level of organization (e.g. the mtDNA molecule), then n, as used in our model, will apply to the number of segregating units not the number of mitochondria per cell (e.g. n = 200 would then apply to a cell with 200 segregating units, which may be a cell with far fewer than 200 mitochondria).
By assuming an infinite population size, a common assumption in studies of this kind [1, 5, 6, 8] we have ignored genetic drift, which can be a powerful force in population genetics. While it is beyond the scope of this study to formally model the effects of genetic drift on the evolution of uniparental inheritance, we can anticipate some of its effects. As the mutation leading to uniparental inheritance has a small advantage when its frequency is low, genetic drift will lead to the frequent loss of those mutations. Thus, the initial invasion of a mutation for uniparental inheritance may be largely determined by genetic drift rather than by positive selection. As the frequency of uniparental inheritance increases, however, so too does its advantage, reducing the probability that the mutation is lost to drift. The potential for rare mutations to be lost to drift is not unique to our model. The genomic conflict hypothesis requires stringent conditions for uniparental inheritance mutations to invade [6, 34]. Under this hypothesis, a mutation for uniparental inheritance must arise within a population that contains selfish mutants but in which the selfish mutant is not fixed. Otherwise, uniparental inheritance cannot become associated with non-selfish mitochondria. Any mutations leading to uniparental inheritance that arise outside of this window will have no selective advantage and will be more likely to be lost by genetic drift [6, 34].
Conclusion
Selection against heteroplasmy has implications for the evolution of the mitochondrial genome. Because of a smaller effective population size, which is more strongly affected by genetic drift, and higher mutation rates, mtDNA should be less conserved than the nuclear genome [35, 36]. Indeed, mitochondrial transfer RNAs and synonymous sites mutate 5–50 times more frequently than comparable elements in the nuclear genome [35, 37]. Because the mitochondrial genome is effectively asexual, any deleterious mutations in the fittest haplotype cannot be rescued (except by unlikely back mutations). This effect, known as Muller's Ratchet, should eventually lead to irreparable genome meltdown [38, 39]. In stark contrast to theoretical predictions, however, mitochondrial coding genes are more conserved than analogous nuclear oxidative phosphorylation genes [36]. When mtDNA mutates, only one of the many mtDNA molecules in the cell is affected, leading to a heteroplasmic cell. Selection against heteroplasmy should reduce the probability that mtDNA mutations spread throughout the cell, which, in turn, should oppose changes to mtDNA. Thus, selection against heteroplasmy may not only explain the evolution of uniparental inheritance but also why mitochondrial coding genes have thus far managed to resist the effects of Muller's Ratchet.
Model
Our model tracks the distribution of cell types through each stage of the life cycle across multiple generations. The redistribution of cell types is based on probability theory, but the model itself is deterministic. We assume that the population is effectively infinite and unaffected by genetic drift, as is regularly assumed in models such as ours [1, 5, 6, 8]. Consequently, the probability that a cell takes a particular state equates to the proportion of that cell type in the population. We take a similar approach to previous models [1, 5], but our model differs slightly in our treatment of mutation. Hastings does not include mutation [5], while Hadjivasiliou and colleagues treat mutation as a one-way process from wild-type to mutant mitochondria in the conflict and mutation clearance models [1]. When examining the mitochondrial-nuclear coadaptation model, however, Hadjivasiliou and colleagues allow mutation to proceed both ways as we have done here [1]. In our model, mutation is designed to capture the ability of a mitochondrial type to mutate from its current state to other haplotypes (one type in our main model and two types in our supplementary model, but an extremely large number of haplotypes in reality).
Diploid cell types are described by the vector Mt,τα=(i,G), where i corresponds to the number of mutant mitochondria and takes values in {0,1…n}, t indicates the generation, and τα indicates the stage of the life cycle. If we know the number of mutant mitochondria (i), the number of wild type mitochondria (which we denote j) is fixed as j = n – i. G indicates the nuclear genotype and takes values in {U1B2,B1B2}. Gametes are described by the vector Mt,τα=(p,g), where p is the number of mutant mitochondria and takes values in {0,1…n / 2} and g represents the nuclear allele and takes values in {U1,B1,B2}. The probability of obtaining a particular diploid cell type is written as P(Mt,τα=(i,G)) and the probability of obtaining a particular gamete is written as P(Mt,τα=(p,g)).
These probabilities can also be thought of as the proportion of the population with that particular cell or gamete type.
There are n+1 total mitochondrial states for diploid cells and n / 2+1 possible mitochondrial states for haploid cells. For the case in which mating type and inheritance loci are linked, the total number of diploid cell types is 2(n+1) while the total number of haploid cell types is 3(n / 2+1). We obtained numerical solutions to our model via scripts that we developed in MATLAB (version 2013b).
Initialization
The starting population is evenly split between B1 and B2 gametes, and all gametes contain type wild type mitochondria (i.e. P(M0,τ1=(0,B1))=0.5,P(M0,τ1=(0,B2))=0.5 and P(M0,τ1=(p,g))=0,∀p>0andg=U1). We first allow this population to reach equilibrium, which we define as the point at which the proportion of cell types change by less than 10−12 (except when the probability that a mitochondrion mutates into another mitochondrion is 10−10 (μ = 10−10), in which case we define equilibrium to be a change of less than 10−13). We then introduce U1 gametes that are homoplasmic for wild type mitochondria by setting P(Mge1,τ1=(0,U1))=0.01, where ge1 is the number of generations taken to reach the first equilibrium. To maintain the total proportion of the population at 1, we remove the corresponding proportion of cells from the B1 population (i.e.P(Mge1,τ1=(0,U1))=P(Mge1,τ1=(0,U1))−0.01). In two instances, we alter the way in which U1 is introduced. In S4 Fig, we introduce U1 into the most heteroplasmic gamete with a frequency greater than 0.01, and in S5 Fig we vary the introductory frequency of U1. Our life cycle is very similar to the life cycle used by Hadjivasiliou and colleagues [1], which examined the genomic conflict, mutational clearance, and mitochondrial-nuclear coadaptation hypotheses.
Random mating
Gametes with n / 2 mitochondria randomly mate with the opposite mating type to produce diploid cells containing n mitochondria. In effect, this is random mating in which all matings between the same mating type (i.e. U1U1, B1B1, B2B2 and U1B1) are lethal, and the only viable genotypes are U1B2 and B1B2.
Biparental mating
Consider a biparental mating involving a gamete in state Mt,τ1=(p,B1), where τ1 is the gamete stage of the life cycle. For this gamete to produce a diploid cell with type Mt,τ2=(i,B1B2), where τ2 is the diploid cell stage of the life cycle that precedes mutation, it must mate with a gamete of type Mt,τ1=(i−p,B2). The probability of this mating is 2P(Mt,τ1=(p,B1))P(Mt,τ1=(i−p,B2)), where the factor of 2 accounts for the two ways in which we can choose B1 and B2 (B1 then B2 or B2 then B1). We restrict the values of p and i – p to biologically valid combinations. First, 0 ≤ p ≤ n / 2, as the B1 gamete cannot carry negative numbers of mutant mitochondria nor can it contain more mutant mitochondria than the total number of mitochondria in the gamete. Likewise, 0 ≤ i – p ≤ n / 2 for the B2 gamete, which, when rearranged, gives i – (n / 2) ≤ p ≤ i. Valid values for p lie in the range of intersection of these two inequalities, giving max(0,i – (n / 2)) ≤ p ≤ min(n / 2,i).
We can thus obtain the probability of forming any given diploid cell type after random mating with the sum,
Uniparental mating
Because uniparental matings between U1 and B2 gametes contain mitochondria from U1 alone, U1B2 cells initially have n / 2 mitochondria. To restore the total complement of n mitochondria, we sample n / 2 mitochondria with replacement from the n / 2 mitochondria in the U1B2 cell and add the n / 2 sampled mitochondria to the original set of mitochondria to form a cell with n mitochondria.
For a gamete with identity Mt,τ1=(p,U1) to produce a diploid cell with identity Mt,τ2=(i,U1B2), it must sample n / 2 mitochondria containing i – p mutant mitochondria and n / 2 – (i – p) wild type mitochondria. The mitochondrial state of the B2 gamete is irrelevant because its mitochondria are discarded and we will refer to this cell as Mt,τ1=(r,B2).
Sampling of the n / 2 mitochondria follows a binomial distribution, which we denote T(i – p;n / 2,(2p) / n), where i – p refers to the number of mutant mitochondria that need to be sampled, n / 2 refers to the number of mitochondria being sampled, and (2p) / n is the probability of drawing a single mutant mitochondrion from a U1B2 cell with p (out of n / 2) mutant mitochondria (where (2p) / n is obtained by rearranging p / (n / 2)).
The probability of sampling i – p mutant mitochondria (and (n / 2) – (i – p) wild type mitochondria) is given by
The restrictions on p and i – p are the same as those in biparental mating. Since U1 will form the same initial U1B2 cell regardless of the B2 gamete with which it mates, the probability of producing each type of U1 gamete is multiplied by the probability of selecting any B2 gamete. The probability of forming a given U1B2 cell after random mating is determined by
Mutation
We denote the post-mutation states of cells as Mt,τ3=(i,G), (where τ3 indicates the post-mutation life cycle stage). If we define the number of wild type mitochondria that mutate to mutant mitochondria to be a and the number of mutant mitochondria that mutate to wild type mitochondria as b, a post-mutation cell in state Mt,τ3=(i,G) must be derived from a pre-mutation cell in state Mt,τ2=(i−a+b,G) (because the pre-mutation cell gains a mutant mitochondria and loses b mutant mitochondria to form the post-mutation cell). Similarly, if the post-mutation cell has j wild type mitochondria, then the pre-mutation cell must have j + a – b wild type mitochondria, where j = n – i.
First, we must work out the probability that a cell mutates a of its wild type mitochondria to mutant mitochondria. We define Y(a;n – i + a – b,μ) as the probability that a pre-mutation cell has a mutations in its n – i + a – b wild type mitochondria given that each mitochondrion mutates with probability μ. The accumulation of mutations is binomially distributed such that
Similarly, we define Y(b;i – a + b,μb) to be the probability that a pre-mutation cell acquires b mutations in its i – a + b mutant mitochondria given that each mitochondrion mutates with probability μb. This probability is given by
For any combination of values for a, b and i, multiplying Y(a;n – i + a – b,μ) by Y(b;i – a + b,μb) gives the probability of a particular transition from a pre-mutation cell with identity Mt,τ3=(i−a+b,G) to a post-mutation cell with identity Mt,τ3=(i,G). To get the overall probability that such a transition occurs, we multiply the probability of the transition by the proportion of pre-mutation cells in the population. To produce the post-mutation population, we sum all possible transitions between pre-mutation and post-mutation cells. All valid transitions must satisfy 0 ≤ a ≤ i (because the post-mutation cell cannot receive more than i mutant mitochondria) and 0 ≤ b ≤ n – i (because the post-mutation cell cannot receive more than n – i wild type mitochondria). Thus, we can determine the post-mutation population by
In the neutral scenario, μ = μb (i.e. the rate of mutation from wild type to mutant is equal to the rate of mutation from mutant to wild type).
Selection
The relative fitness of a cell, w(i), is a measure of how likely a cell type is to survive and reproduce, and we assume that cells carrying multiple mitochondrial types have lower fitness. For the first fitness function, the relative fitness of a cell with i mutant mitochondria is determined according to the following piecewise concave function:
for even values of n and 0 ≤ ch ≤ 1, where ch is the cost of heteroplasmy. In this function, a cell containing n / 2 mutant and n / 2 wild type mitochondria has minimum relative fitness.The post-selection population of each cell type is then given by:
We also make use of two alternative fitness functions. The first of these is the piecewise linear function:
The third fitness function is the piecewise convex function:
We normalize the post-selection population by
where so that the sum of the proportions of the population equals 1.Meiosis
The cell must first duplicate its chromosomes and double its mitochondrial complement (from n to 2n). This cell with 2n mitochondria then produces gametes with n / 2 mitochondria. Meiosis occurs in two steps. First, we sample n mitochondria with replacement from a cell containing n mitochondria and add the set of sampled mitochondria to the original set of mitochondria to form a cell containing 2n mitochondria (this is the same process that occurs in uniparental mating only with n mitochondria rather than n / 2 mitochondria). We let Mt,τ6=(l,2G) represent the cell with doubled mitochondria and nuclear genotype, where l takes values in {0,1…2n} and 2G takes values in {U1U1B2B2,B1B1B2B2}.
For a cell to contain l mutant mitochondria after duplication of its mitochondria, it must sample l – i mutant mitochondria. We denote the probability of sampling l – i mutant mitochondria from Mt,τ5=(i,G) as F(l – i;n,i / n). Sampling follows a binomial distribution such that
We obtain Mt,τ6=(l,2G) by
During the second step of meiosis, the cells with 2n mitochondria produce gametes with n / 2 mitochondria. Biologically, this occurs in two steps. In meiosis 1, the homologous chromosomes are pulled apart to produce two haploid cells that contain two identical nuclear alleles (sister chromatids) and n mitochondria. In meiosis 2, the two cells divide to produce four gametes, each with a single nuclear allele and n / 2 mitochondria. Since mitochondria segregate independently of nuclear alleles during cell partitioning, we model this as a single step.
We define S(p;2n,l,n / 2) to be the probability of obtaining p mutant mitochondria in n / 2 draws from a cell in state Mt,τ6=(l,m,2G). Here, sampling is without replacement and follows a hypergeometric distribution, giving
Gametes produced by meiosis are represented by Mt+1,τ1=(p,g). We determine the probability of obtaining a particular gamete using
andFactors of 1 / 2 in the above three equations take into account that half of the gametes produced from parent cells with nuclear genotype U1B2 will carry the U1 allele and the other half will carry the B2 allele (with similar logic applied for gametes produced from parent cells with nuclear genotype B1B2). Meiosis completes a single generation of the life cycle.
Relative fitness of cells
The relative fitness of U1B2 cells is given by
while the relative fitness of B1B2 cells isRelative fitness of gametes
Although gametes are not subject to selection in our model, and thus do not technically have fitness values, it is informative to track gamete relative fitness throughout the simulation. We define a gamete’s relative fitness as the fitness that a diploid cell would have if it had the same mitochondrial composition as the gamete. Since gametes contain n / 2 mitochondria, they will have minimum fitness when they carry n / 4 wild type and n / 4 mutant mitochondria. To rescale the fitness function, we substitute n / 2 for n in the diploid cell fitness functions. For example, Equation (1) becomes
Once the fitness function is scaled to gametes, we can determine the relative fitness of the three gametes by
andSee S1–S6 Model for details of the other models.
Supporting Information
Zdroje
1. Hadjivasiliou Z, Lane N, Seymour RM, Pomiankowski A. Dynamics of mitochondrial inheritance in the evolution of binary mating types and two sexes. Proc R Soc Lond B Biol Sci. 2013;280(1769):20131920-. doi: 10.1098/rspb.2013.1920 23986113
2. Mishra P, Chan DC. Mitochondrial dynamics and inheritance during cell division, development and disease. Nat Rev Mol Cell Biol. 2014;15(10):634–46. doi: 10.1038/nrm3877 25237825
3. Grun P. Cytoplasmic genetics and evolution. New York: Columbia University Press; 1976.
4. Cosmides LM, Tooby J. Cytoplasmic inheritance and intragenomic conflict. J Theor Biol. 1981;89(1):83–129. 7278311
5. Hastings IM. Population genetic-aspects of deleterious cytoplasmic genomes and their effect on the evolution of sexual reproduction. Genet Res. 1992;59(3):215–25. 1511870
6. Law R, Hutson V. Intracellular symbionts and the evolution of uniparental cytoplasmic inheritance. Proc R Soc Lond B Biol Sci. 1992;248(1321):69–77. 1355912
7. Bergstrom CT, Pritchard J. Germline bottlenecks and the evolutionary maintenance of mitochondrial genomes. Genetics. 1998;149(4):2135–46. 9691064
8. Hadjivasiliou Z, Pomiankowski A, Seymour RM, Lane N. Selection for mitonuclear co-adaptation could favour the evolution of two sexes. Proc R Soc Lond B Biol Sci. 2012;279(1734):1865–72. doi: 10.1098/rspb.2011.1871 22158961
9. Birky CW. Uniparental inheritance of mitochondrial and chloroplast genes—mechanisms and evolution. Proc Natl Acad Sci USA. 1995;92(25):11331–8. 8524780
10. Birky CW, Strausberg RL, Perlman PS. Vegetative segregation of mitochondria in yeast: estimating parameters using a random model. Mol Gen Genet. 1978;158(3):251–61.
11. Zouros E, Ball AO, Saavedra C, Freeman KR. An unusual type of mitochondrial DNA inheritance in the blue mussel Mytilus. Proc Natl Acad Sci USA. 1994;91(16):7463–7. 8052604
12. Sharpley MS, Marciniak C, Eckel-Mahan K, McManus M, Crimi M, Waymire K, et al. Heteroplasmy of mouse mtDNA is genetically unstable and results in altered behavior and cognition. Cell. 2012;151(2):333–43. doi: 10.1016/j.cell.2012.09.004 23063123
13. Rand DM. The units of selection on mitochondrial DNA. Annu Rev Ecol Syst. 2001;32 : 415–48.
14. Eyre-Walker A, Keightley PD. The distribution of fitness effects of new mutations. Nature Reviews Genetics. 2007;8(8):610–8. 17637733
15. Rossignol R, Faustin B, Rocher C, Malgat M, Mazat JP, Letellier T. Mitochondrial threshold effects. Biochem J. 2003;370(Pt 3):751–62. Epub 2002/12/07. 12467494
16. Hoffmann HP, Avers CJ. Mitochondrion of yeast: Ultrastructural evidence for one giant, branched organelle per cell. Science. 1973;181(4101):749–51. 4579683
17. Beckers MC, Munaut C, Minet A, Matagne RF. The fate of mitochondrial DNAs of mt+ and mt - origin in gametes and zygotes of Chlamydomonas. Curr Genet. 1991;20(3):239–43. Epub 1991/08/01. 1934130
18. Moriyama Y, Kawano S. Rapid, selective digestion of mitochondrial DNA in accordance with the matA hierarchy of multiallelic mating types in the mitochondrial inheritance of Physarum polycephalum. Genetics. 2003;164(3):963–75. 12871907
19. Silliker ME, Liles JL, Monroe JA. Patterns of mitochondrial inheritance in the myxogastrid Didymium iridis. Mycologia. 2002;94(6):939–46. 21156568
20. Nakamura S. Paternal inheritance of mitochondria in Chlamydomonas. J Plant Res. 2010;123(2):163–70. doi: 10.1007/s10265-009-0295-8 20069335
21. Neale DB, Sederoff RR. Paternal inheritance of chloroplast DNA and maternal inheritance of mitochondrial DNA in loblolly pine. Theor Appl Genet. 1989;77(2):212–6. Epub 1989/02/01. doi: 10.1007/BF00266189 24232531
22. Hurst LD, Hamilton WD. Cytoplasmic fusion and the nature of sexes. Proc R Soc Lond B Biol Sci. 1992;247(1320):189–94.
23. Denver DR, Morris K, Lynch M, Vassilieva LL, Thomas WK. High direct estimate of the mutation rate in the mitochondrial genome of Caenorhabditis elegans. Science. 2000;289(5488):2342–4. 11009418
24. Lynch M, Sung W, Morris K, Coffey N, Landry CR, Dopman EB, et al. A genome-wide view of the spectrum of spontaneous mutations in yeast. Proc Natl Acad Sci USA. 2008;105(27):9272–7. doi: 10.1073/pnas.0803466105 18583475
25. Haag-Liautard C, Coffey N, Houle D, Lynch M, Charlesworth B, Keightley PD. Direct estimation of the mitochondrial DNA mutation rate in Drosophila melanogaster. PLoS Biol. 2008;6(8):e204. doi: 10.1371/journal.pbio.0060204 18715119
26. Ephrussi B. Nucleocytoplasmic relations in microorganisms. Oxford: Clarendon Press; 1953.
27. Lane N. The problem with mixing mitochondria. Cell. 2012;151(2):246–8. doi: 10.1016/j.cell.2012.09.028 23063117
28. Fan W, Waymire KG, Narula N, Li P, Rocher C, Coskun PE, et al. A Mouse Model of Mitochondrial Disease Reveals Germline Selection Against Severe mtDNA Mutations. Science. 2008;319(5865):958–62. doi: 10.1126/science.1147786 18276892
29. Park JS, Sharma LK, Li H, Xiang R, Holstein D, Wu J, et al. A heteroplasmic, not homoplasmic, mitochondrial DNA mutation promotes tumorigenesis via alteration in reactive oxygen species generation and apoptosis. Hum Mol Genet. 2009;18(9):1578–89. doi: 10.1093/hmg/ddp069 19208652
30. Picard M, Zhang J, Hancock S, Derbeneva O, Golhar R, Golik P, et al. Progressive increase in mtDNA 3243A>G heteroplasmy causes abrupt transcriptional reprogramming. Proc Natl Acad Sci USA. 2014;111(38):E4033–E42. doi: 10.1073/pnas.1414028111 25192935
31. Wallace DC. Why do we still have a maternally inherited mitochondrial DNA? Insights from evolutionary medicine. Annu Rev Biochem. 2007;76 : 781–821. 17506638
32. Poe BG III, Duffy CF, Greminger MA, Nelson BJ, Arriaga EA. Detection of heteroplasmy in individual mitochondrial particles. Anal Bioanal Chem. 2010;397(8):3397–407. doi: 10.1007/s00216-010-3751-3 20467729
33. Gilkerson RW, Schon EA, Hernandez E, Davidson MM. Mitochondrial nucleoids maintain genetic autonomy but allow for functional complementation. J Cell Biol. 2008;181(7):1117–28. doi: 10.1083/jcb.200712101 18573913
34. Hoekstra RF. Evolution of uniparental inheritance of cytoplasmic DNA. In: Maynard Smith J, Vida G, editors. Organizational constraints on the dynamics of evolution. New York: Manchester University Press; 1990.
35. Lynch M. Mutation accumulation in transfer RNAs: Molecular evidence for Muller's ratchet in mitochondrial genomes. Mol Biol Evol. 1996;13(1):209–20.. 8583893
36. Popadin KY, Nikolaev SI, Junier T, Baranova M, Antonarakis SE. Purifying selection in mammalian mitochondrial protein-coding genes is highly effective and congruent with evolution of nuclear genes. Mol Biol Evol. 2013;30(2):347–55. doi: 10.1093/molbev/mss219 22983951
37. Lynch M. The origins of genome architecture: Sinauer Associates Inc; 2007.
38. Muller HJ. The relation of recombination to mutational advance. Mutation Research/Fundamental and Molecular Mechanisms of Mutagenesis. 1964;1(1):2–9.
39. Felsenstein J. The evolutionary advantage of recombination. Genetics. 1974;78(2):737–56. 4448362
Štítky
Genetika Reprodukční medicína
Článek Retraction: Astakine 2—the Dark Knight Linking Melatonin to Circadian Regulation in CrustaceansČlánek Adventures in WonderlandČlánek Genomic Location of the Major Ribosomal Protein Gene Locus Determines Global Growth and InfectivityČlánek Spatial Fluctuations in Expression of the Heterocyst Differentiation Regulatory Gene in FilamentsČlánek Genome-Wide Negative Feedback Drives Transgenerational DNA Methylation Dynamics in ArabidopsisČlánek Systematic Dissection of the Sequence Determinants of Gene 3’ End Mediated Expression ControlČlánek The Chromatin Remodeler CHD8 Is Required for Activation of Progesterone Receptor-Dependent EnhancersČlánek The DNA Helicase Recql4 Is Required for Normal Osteoblast Expansion and Osteosarcoma FormationČlánek Dual-Specificity Anti-sigma Factor Reinforces Control of Cell-Type Specific Gene Expression in
Článek vyšel v časopisePLOS Genetics
Nejčtenější tento týden
2015 Číslo 4- Souvislost haplotypu M2 genu pro annexin A5 s opakovanými reprodukčními ztrátami
- Jak zlepšit účinnost psychofarmakoterapie a adherenci k ní pomocí farmakogenetiky? – kazuistiky z české praxe
- Akutní intermitentní porfyrie
- Spolehlivost LH testů
- Doc. Eva Vlčková: Transthyretinová amyloidóza již díky moderní terapii nemusí být fatální diagnózou, musíme ji však zachytit a léčit včas
-
Všechny články tohoto čísla
- Retraction: Astakine 2—the Dark Knight Linking Melatonin to Circadian Regulation in Crustaceans
- Adventures in Wonderland
- Experimental Swap of 's Assortative Mating Preferences Demonstrates Key Role of X-Chromosome Divergence Island in Incipient Sympatric Speciation
- Chromosome Replacement and Deletion Lead to Clonal Polymorphism of Berry Color in Grapevine
- The Protein Quality Control Machinery Regulates Its Misassembled Proteasome Subunits
- Genome-Wide Association Study Identifies as a Critical Gene for Susceptibility to Noise-Induced Hearing Loss
- Genomic Location of the Major Ribosomal Protein Gene Locus Determines Global Growth and Infectivity
- Viable Neuronopathic Gaucher Disease Model in Medaka () Displays Axonal Accumulation of Alpha-Synuclein
- Multi-locus Analysis of Genomic Time Series Data from Experimental Evolution
- The Genetic Legacy of the Expansion of Turkic-Speaking Nomads across Eurasia
- Lack of GDAP1 Induces Neuronal Calcium and Mitochondrial Defects in a Knockout Mouse Model of Charcot-Marie-Tooth Neuropathy
- The Pif1 Helicase, a Negative Regulator of Telomerase, Acts Preferentially at Long Telomeres
- Inhibiting K63 Polyubiquitination Abolishes No-Go Type Stalled Translation Surveillance in
- SYD-1C, UNC-40 (DCC) and SAX-3 (Robo) Function Interdependently to Promote Axon Guidance by Regulating the MIG-2 GTPase
- Spatial Fluctuations in Expression of the Heterocyst Differentiation Regulatory Gene in Filaments
- Synergistic and Independent Actions of Multiple Terminal Nucleotidyl Transferases in the 3’ Tailing of Small RNAs in Arabidopsis
- Host Genetic Variation Influences Gene Expression Response to Rhinovirus Infection
- Contribution of Large Region Joint Associations to Complex Traits Genetics
- Volatility of Mutator Phenotypes at Single Cell Resolution
- Proteolysis of Virulence Regulator ToxR Is Associated with Entry of into a Dormant State
- Genome-Wide Negative Feedback Drives Transgenerational DNA Methylation Dynamics in Arabidopsis
- A Multi-layered Protein Network Stabilizes the FtsZ-ring and Modulates Constriction Dynamics
- Systematic Dissection of the Sequence Determinants of Gene 3’ End Mediated Expression Control
- Genome Sequencing of the Perciform Fish Provides Insights into Molecular and Genetic Mechanisms of Stress Adaptation
- Natural Variant E610G Is a Semi-dominant Suppressor of IAP-Induced RNA Processing Defects
- The Alkaline Response Pathway: Identification of a Novel Rim Pathway Activator
- Transgenerational Inheritance of Diet-Induced Genome Rearrangements in Drosophila
- A Single Nucleotide Polymorphism Uncovers a Novel Function for the Transcription Factor Ace2 during Hyphal Development
- DNA Damage Response and Spindle Assembly Checkpoint Function throughout the Cell Cycle to Ensure Genomic Integrity
- The Functional Interplay Between the t(9;22)-Associated Fusion Proteins BCR/ABL and ABL/BCR in Philadelphia Chromosome-Positive Acute Lymphatic Leukemia
- Extreme Recombination Frequencies Shape Genome Variation and Evolution in the Honeybee,
- Beyond Glycolysis: GAPDHs Are Multi-functional Enzymes Involved in Regulation of ROS, Autophagy, and Plant Immune Responses
- Comprehensive Profiling of Amino Acid Response Uncovers Unique Methionine-Deprived Response Dependent on Intact Creatine Biosynthesis
- Windpipe Controls Intestinal Homeostasis by Regulating JAK/STAT Pathway via Promoting Receptor Endocytosis and Lysosomal Degradation
- Ataxin-2 Regulates Translation in a New BAC-SCA2 Transgenic Mouse Model
- Cross-Population Joint Analysis of eQTLs: Fine Mapping and Functional Annotation
- The Power of Gene-Based Rare Variant Methods to Detect Disease-Associated Variation and Test Hypotheses About Complex Disease
- The Chromatin Remodeler CHD8 Is Required for Activation of Progesterone Receptor-Dependent Enhancers
- Competition between VanU Repressor and VanR Activator Leads to Rheostatic Control of Vancomycin Resistance Operon Expression
- A Missense Change in the Gene Links Aberrant Autophagy to a Neurodegenerative Vacuolar Storage Disease
- Simultaneous Discovery, Estimation and Prediction Analysis of Complex Traits Using a Bayesian Mixture Model
- Selection against Heteroplasmy Explains the Evolution of Uniparental Inheritance of Mitochondria
- Genome-Destabilizing Effects Associated with Top1 Loss or Accumulation of Top1 Cleavage Complexes in Yeast
- Imputation-Based Population Genetics Analysis of Malaria Parasites
- Heterozygosity for a Hypomorphic Polβ Mutation Reduces the Expansion Frequency in a Mouse Model of the Fragile X-Related Disorders
- Neto-Mediated Intracellular Interactions Shape Postsynaptic Composition at the Neuromuscular Junction
- Ndd1 Turnover by SCF Is Inhibited by the DNA Damage Checkpoint in
- Frameshift Variant Associated with Novel Hoof Specific Phenotype in Connemara Ponies
- The DNA Helicase Recql4 Is Required for Normal Osteoblast Expansion and Osteosarcoma Formation
- Spastin Binds to Lipid Droplets and Affects Lipid Metabolism
- Maintenance of Glia in the Optic Lamina Is Mediated by EGFR Signaling by Photoreceptors in Adult Drosophila
- Auxin Influx Carriers Control Vascular Patterning and Xylem Differentiation in
- Dual-Specificity Anti-sigma Factor Reinforces Control of Cell-Type Specific Gene Expression in
- The Lowe Syndrome Protein OCRL1 Is Required for Endocytosis in the Zebrafish Pronephric Tubule
- Postnatal Loss of Hap1 Reduces Hippocampal Neurogenesis and Causes Adult Depressive-Like Behavior in Mice
- CAPER Is Vital for Energy and Redox Homeostasis by Integrating Glucose-Induced Mitochondrial Functions via ERR-α-Gabpa and Stress-Induced Adaptive Responses via NF-κB-cMYC
- Distinct and Cooperative Activities of HESO1 and URT1 Nucleotidyl Transferases in MicroRNA Turnover in
- The Evolutionary Origination and Diversification of a Dimorphic Gene Regulatory Network through Parallel Innovations in and
- MAPK Signaling Pathway Alters Expression of Midgut ALP and ABCC Genes and Causes Resistance to Cry1Ac Toxin in Diamondback Moth
- Spatio-temporal Remodeling of Functional Membrane Microdomains Organizes the Signaling Networks of a Bacterium
- Asymmetric Transcript Discovery by RNA-seq in . Blastomeres Identifies , a Gene Important for Anterior Morphogenesis
- A Stress-Induced Small RNA Modulates Alpha-Rhizobial Cell Cycle Progression
- Systematic Profiling of Poly(A)+ Transcripts Modulated by Core 3’ End Processing and Splicing Factors Reveals Regulatory Rules of Alternative Cleavage and Polyadenylation
- The UPR Branch IRE1- in Plants Plays an Essential Role in Viral Infection and Is Complementary to the Only UPR Pathway in Yeast
- A Non-canonical RNA Silencing Pathway Promotes mRNA Degradation in Basal Fungi
- Co-chaperone p23 Regulates . Lifespan in Response to Temperature
- Re-replication of a Centromere Induces Chromosomal Instability and Aneuploidy
- Shade Avoidance Components and Pathways in Adult Plants Revealed by Phenotypic Profiling
- Lipid-Induced Epigenomic Changes in Human Macrophages Identify a Coronary Artery Disease-Associated Variant that Regulates Expression through Altered C/EBP-Beta Binding
- PLOS Genetics
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Lack of GDAP1 Induces Neuronal Calcium and Mitochondrial Defects in a Knockout Mouse Model of Charcot-Marie-Tooth Neuropathy
- Proteolysis of Virulence Regulator ToxR Is Associated with Entry of into a Dormant State
- Frameshift Variant Associated with Novel Hoof Specific Phenotype in Connemara Ponies
- Ataxin-2 Regulates Translation in a New BAC-SCA2 Transgenic Mouse Model
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání




























