-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaCommon Inherited Variation in Mitochondrial Genes Is Not Enriched for Associations with Type 2 Diabetes or Related Glycemic Traits
Mitochondrial dysfunction has been observed in skeletal muscle of people with diabetes and insulin-resistant individuals. Furthermore, inherited mutations in mitochondrial DNA can cause a rare form of diabetes. However, it is unclear whether mitochondrial dysfunction is a primary cause of the common form of diabetes. To date, common genetic variants robustly associated with type 2 diabetes (T2D) are not known to affect mitochondrial function. One possibility is that multiple mitochondrial genes contain modest genetic effects that collectively influence T2D risk. To test this hypothesis we developed a method named Meta-Analysis Gene-set Enrichment of variaNT Associations (MAGENTA; http://www.broadinstitute.org/mpg/magenta). MAGENTA, in analogy to Gene Set Enrichment Analysis, tests whether sets of functionally related genes are enriched for associations with a polygenic disease or trait. MAGENTA was specifically designed to exploit the statistical power of large genome-wide association (GWA) study meta-analyses whose individual genotypes are not available. This is achieved by combining variant association p-values into gene scores and then correcting for confounders, such as gene size, variant number, and linkage disequilibrium properties. Using simulations, we determined the range of parameters for which MAGENTA can detect associations likely missed by single-marker analysis. We verified MAGENTA's performance on empirical data by identifying known relevant pathways in lipid and lipoprotein GWA meta-analyses. We then tested our mitochondrial hypothesis by applying MAGENTA to three gene sets: nuclear regulators of mitochondrial genes, oxidative phosphorylation genes, and ∼1,000 nuclear-encoded mitochondrial genes. The analysis was performed using the most recent T2D GWA meta-analysis of 47,117 people and meta-analyses of seven diabetes-related glycemic traits (up to 46,186 non-diabetic individuals). This well-powered analysis found no significant enrichment of associations to T2D or any of the glycemic traits in any of the gene sets tested. These results suggest that common variants affecting nuclear-encoded mitochondrial genes have at most a small genetic contribution to T2D susceptibility.
Published in the journal: . PLoS Genet 6(8): e32767. doi:10.1371/journal.pgen.1001058
Category: Research Article
doi: https://doi.org/10.1371/journal.pgen.1001058Summary
Mitochondrial dysfunction has been observed in skeletal muscle of people with diabetes and insulin-resistant individuals. Furthermore, inherited mutations in mitochondrial DNA can cause a rare form of diabetes. However, it is unclear whether mitochondrial dysfunction is a primary cause of the common form of diabetes. To date, common genetic variants robustly associated with type 2 diabetes (T2D) are not known to affect mitochondrial function. One possibility is that multiple mitochondrial genes contain modest genetic effects that collectively influence T2D risk. To test this hypothesis we developed a method named Meta-Analysis Gene-set Enrichment of variaNT Associations (MAGENTA; http://www.broadinstitute.org/mpg/magenta). MAGENTA, in analogy to Gene Set Enrichment Analysis, tests whether sets of functionally related genes are enriched for associations with a polygenic disease or trait. MAGENTA was specifically designed to exploit the statistical power of large genome-wide association (GWA) study meta-analyses whose individual genotypes are not available. This is achieved by combining variant association p-values into gene scores and then correcting for confounders, such as gene size, variant number, and linkage disequilibrium properties. Using simulations, we determined the range of parameters for which MAGENTA can detect associations likely missed by single-marker analysis. We verified MAGENTA's performance on empirical data by identifying known relevant pathways in lipid and lipoprotein GWA meta-analyses. We then tested our mitochondrial hypothesis by applying MAGENTA to three gene sets: nuclear regulators of mitochondrial genes, oxidative phosphorylation genes, and ∼1,000 nuclear-encoded mitochondrial genes. The analysis was performed using the most recent T2D GWA meta-analysis of 47,117 people and meta-analyses of seven diabetes-related glycemic traits (up to 46,186 non-diabetic individuals). This well-powered analysis found no significant enrichment of associations to T2D or any of the glycemic traits in any of the gene sets tested. These results suggest that common variants affecting nuclear-encoded mitochondrial genes have at most a small genetic contribution to T2D susceptibility.
Introduction
Mitochondrial dysfunction has been implicated in both rare and common forms of type 2 diabetes (T2D) [1]–[4]. Individuals with T2D contain less mitochondria in their skeletal muscle [5], [6], and impaired mitochondrial function has been associated with T2D and insulin resistance, an intermediate phenotype and risk factor of diabetes [7]. In particular, oxidative phosphorylation (OXPHOS) activity in mitochondria, central for energy production in the cell, is reduced in certain populations of diabetic and insulin-resistant individuals [5], [8]. Furthermore, we found that the expression of OXPHOS genes is coordinately downregulated in diabetic versus healthy muscle [9], [10]. It has been proposed that decreased OXPHOS activity may contribute to T2D development by causing fatty acid accumulation in muscle cells, which in turn may inhibit insulin-stimulated glucose uptake [1], [2], [7], [8], [11], or by indirectly reducing glucose-stimulated insulin secretion from pancreatic ß-cells due to a decrease in ATP production [1]. However, it is still not clear whether the molecular and physiologic associations of mitochondria with diabetes are a cause or effect of the common form of T2D [1], [2], [12].
One way to test whether mitochondrial genes play a causal role in the pathogenesis of T2D is to search for inherited DNA variants in mitochondrial genes that influence T2D risk. Proof of concept comes from rare mutations in mitochondrial DNA (mtDNA) that cause Maternally Inherited Diabetes with Deafness (OMIM #520000). This raises the question of whether inherited variants affecting mitochondrial biology play a more general causal role in the common form of T2D. Candidate gene studies of mitochondria-related genes have yet to conclusively demonstrate (at genome-wide significance) that common variants in nuclear-encoded mitochondrial genes or transcriptional regulators of mitochondrial genes associate with T2D risk [13]–[15]. Also, we published a systematic scan for associations of common single-nucleotide polymorphisms (SNPs) in mtDNA (that encodes 13 genes) that failed to identify significant associations with T2D [16].
Recently, several genome-wide association (GWA) studies of ∼2,000 to 5,000 individuals [17]–[19], and a meta-analysis of 10,128 individuals [20], all of European descent, have identified ∼18 common nuclear DNA variants robustly associated with T2D that collectively explain ∼6% of the genetic contribution to T2D risk. While these associations suggest genes involved in various biological processes, such as WNT signaling, NOTCH signaling and the cell cycle, none have implicated mitochondrial processes. The only gene with a mitochondrial isoform near a validated T2D SNP is the insulin-degrading enzyme, IDE (Entrez ID 3416), but it exerts its insulin degrading activity primarily in the cytoplasm [21].
Given the large number of nuclear-encoded mitochondrial genes (∼1,000 known based on the mitochondrial protein compendium MitoCarta [22]) and the largely unexplained genetic basis of T2D, it is possible that many (tens or hundreds of) common variants in or near mitochondrial genes are associated with T2D. While each gene might have a modest effect too small to be detected on its own, together they could have a more substantial collective impact. It is also possible that several nuclear regulators of mitochondrial genes could harbor common variants of modest effects on T2D risk.
These hypotheses could be tested using a Gene Set Enrichment Analysis (GSEA) approach applied to genetic variant association data [23]. We originally described GSEA to test whether predefined biological processes or gene sets are enriched for genes with coordinate modest expression differences between two samples, differences that are hard to detect when inspecting each gene separately [9], [24]. In fact, GSEA was first used to show that OXPHOS genes are collectively downregulated in human muscle in diabetic compared to non-diabetic individuals [9].
In the context of genetic association data, GSEA has been suggested to be a promising approach to identify sets of functionally related genes, such as biological pathways, enriched for associations of modest effects (hard to detect with single-marker analysis) on a polygenic disease or trait [23]. Several groups have begun to apply different variations of GSEA to GWA studies to study disorders such as Parkinson's disease [23], dyslipidemia [25], T2D [26]–[28], Crohn's disease [25], [29], [30], and multiple sclerosis [31]. While the principal concept is similar in these studies, alternative implementations differ substantially, for example in how genes are scored or enrichment is evaluated. In addition, researchers have only begun to evaluate the ranges of parameters (e.g. effect size or fraction of causal genes) under which gene-set approaches have power to identify associations not found by single-variant analysis [32], [33].
To maximize power, it is critical to make use of meta-analyses of multiple independent GWA studies whose increasing sample size (from thousands of people in single studies to tens of thousands in meta-analyses) boosts the statistical power for detecting clustering of modest associations. Yet, as opposed to traditional GWA studies, information about individual genotypes is not available for most meta-analyses, making it impossible to evaluate statistical significance through standard phenotype permutation analysis. While several GSEA variations have been recently applied to meta-analyses, the extent to which they account for confounding effects on gene association scores has not been tested.
Here we introduce a GSEA approach applied to genome-wide variant association data, which we named “Meta-Analysis Gene-set Enrichment of variaNT Associations” (MAGENTA). MAGENTA does not require genotype data, making it especially relevant to GWA study meta-analyses. We tested and validated MAGENTA using the Diabetes Genetics Initiative (DGI) GWA study [17], and three GWA meta-analyses of cholesterol and lipid blood levels [34]. Using simulations, we identified the conditions under which our method has increased power to detect associations for which there is low detection power with single SNP analysis. Finally, to test whether mitochondrial dysfunction may be causal to T2D, we applied MAGENTA to a set of known nuclear regulators of mitochondrial genes [35], the OXPHOS genes [9], and all known (∼1,000) autosomal human mitochondrial genes [22], using the latest T2D meta-analysis of a total of 47,117 individuals (DIAGRAM+) [36], as well as meta-analyses (up to 46,186 individuals) of seven glucose and insulin-related traits relevant to T2D pathogenesis (MAGIC; [37], [38], Soranzo N. et al., unpublished data).
Results
Meta-Analysis Gene-set Enrichment of variaNT Associations (MAGENTA) evaluates pre-specified gene sets for enrichment of modest associations with a complex disease or trait. MAGENTA consists of four main steps: First, DNA variants, e.g. single-nucleotide polymorphisms (SNPs), are mapped onto genes (Figure 1A). Second, each gene is assigned a gene association score that is a function of its regional SNP association p-values (Figure 1B). Third, confounding effects on gene association scores are identified and corrected for, without requiring genotype data (enabling use of meta-analyses or other types of GWA studies where only variant association statistics are available) (Figure 1C). Fourth, a Gene Set Enrichment Analysis (GSEA)-like statistical test is applied to predefined biologically relevant gene sets to determine whether any of the gene sets are enriched for highly ranked gene association scores compared to randomly sampled gene sets of identical size from the genome (Figure 1D). These four steps are described below, and further detailed in the Materials and Methods section.
Fig. 1. Description of Meta-Analysis Gene-set Enrichment of variaNT Associations (MAGENTA) method. 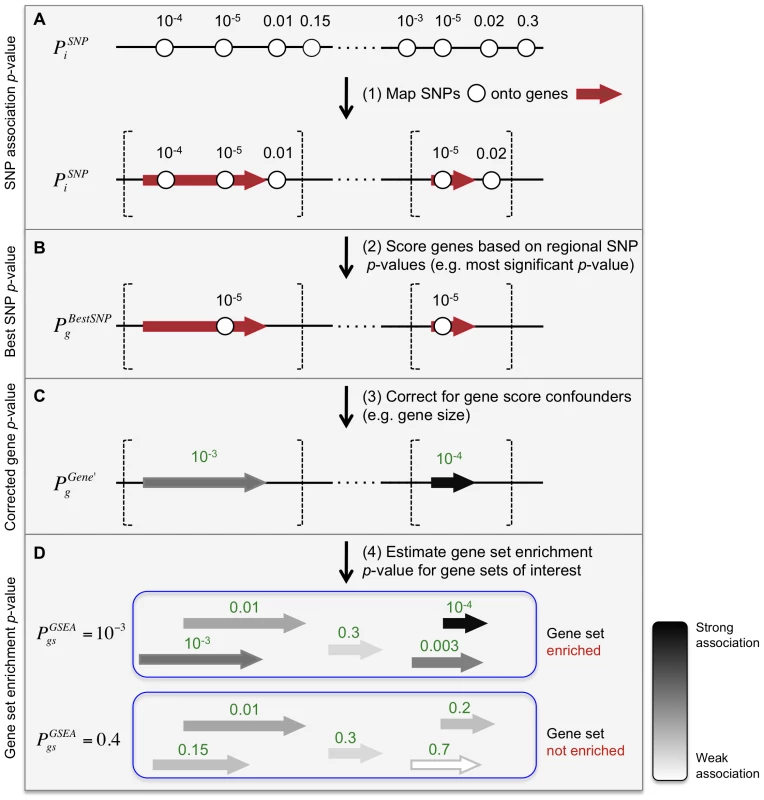
(A) Step 1: Map genetic variants and their association scores onto genes. MAGENTA uses as input the association z-scores or p-values of DNA sequence variants across the entire genome. In this work, we used association p-values of single-nucleotide polymorphisms, SNPs (circles) from a genome-wide association study or meta-analysis, denoted as for SNP i. Gene boundaries (vertical dashed lines) are defined here as predetermined physical distances added upstream and downstream to the most extreme transcript start and end sites of the gene (red arrow), respectively. Linkage-based distances can also be used. Each gene is assigned a set of SNPs that fall in its gene region boundaries. Two genes are shown for simplicity. (B) Step 2: Score genes based on their local SNP . Here the most significant of all SNPs i that lie within the extended gene boundaries is assigned to each gene g in the genome (). (C) Step 3: Correct for confounding effects on the gene score, in the absence of genotype data. In this study we used step-wise multivariate linear regression analysis to regress out of the confounding effects of several physical and genetic properties of genes (listed in Table 1); refers to the corrected gene p-value for gene g. In cases where two genes are assigned the same best SNP p-value, tends to be more significant for small genes than for large genes. (D) Step 4: Calculate a gene set enrichment p-value for each biological pathway or gene set of interest. We used a non-parametric statistical test to test whether for all genes in gene set gs are enriched for highly ranked gene scores more than would be expected by chance, compared to randomly sampled gene sets of identical size from the genome. refers to the nominal gene set enrichment p-value for gene set gs. From SNPs to genes: scoring genes based on SNP association scores
To analyze genetic association data at the level of genes and gene sets, we first needed to compute a gene score based on local SNPs. We assigned to each gene g in the genome a set of SNPs that lie within 110 kilobase (kb) upstream and 40 kb downstream of the gene's most extreme transcript boundaries, in attempt to capture signals from potential causal variants affecting regulatory elements, in addition to coding sequence (Figure 1A; see Materials and Methods for boundary choice). Each gene g is then assigned a score , defined in this instantiation as the most significant p-value among the association p-values of all individual SNPs i within the extended gene boundaries (Figure 1B). We used the best SNP rather than an average value, as we expect only one or a few associated variants per gene.
When was calculated for all 966 nuclear-encoded mitochondrial genes using the T2D DIAGRAM+ GWA meta-analysis, we found that their scores were on average less significant than random (Figure S1). Observing that the mitochondrial genes are smaller on average than all other genes in the genome (Table S1), we next examined the effect of confounders on the most significant SNP p-value per gene, . Towards this goal, we generated 1,000 null distributions of gene scores, through phenotype permutations of the Diabetes Genetics Initiative (DGI) GWA study, for which we have access to genotype data (see Materials and Methods). In these randomized data sets no genome-wide significant associations are expected. We observed significant correlations of the scores for each gene across permutations (mean Pearson's correlation coefficient across all genes for pairs of permutations: r = 0.36). This suggested that inherent properties of genes (not specific to the phenotype studied) confound gene scores.
When we explicitly tested the potential confounding role of gene size, previously suggested [23], [25], we observed that large genes tended to receive more significant scores than small genes in the randomized data set (Figure S2).
Correcting for confounding effects on gene association scores in the absence of genotype data
When genotype data are available, such as in individual GWA studies, confounding effects on , e.g. gene size, can be corrected for using phenotype permutation analysis that does not require a priori knowledge of the confounders (described in Materials and Methods). However, to exploit the power of large GWA study meta-analyses, where permutation analysis cannot be performed due to unavailability of genotype data, we needed an alternative correction method. We chose a linear regression-based approach that adjusts for the effects of multiple confounders on the gene score. This required identifying a substantial amount of the confounding effects on .
To find confounders on we systematically tested for correlations between the unadjusted gene score, calculated from permuted DGI GWA study (see Materials and Methods) and six potential gene score confounders (listed in Table 1; correlations reported for z-scores). We examined both physical properties of genes - physical gene size and number of SNPs per kilobase for each gene, and genetic properties that consider the dependency between subsets of SNPs due to genetic linkage between proximal markers. The genetic properties tested included estimated number of independent SNPs per gene (SNPs in linkage equilibrium), number of recombination hotspots spanning each gene, genetic distance of the gene, and linkage disequilibrium (LD) unit distance per gene, normalized to the size of the gene and its extended boundaries (see Materials and Methods). We found significant correlations for all six properties tested (average values across 1,000 permuted data sets: 0.17<r<0.38; p<2e-70) (Table 1), suggesting that all variables may have a confounding effect on . A similar trend was observed using from the actual DGI GWA study (Table 1, column 2; 0.14<r<0.39, p<1e-74), and the T2D GWA meta-analysis, used below to test the mitochondria-diabetes hypothesis (Table S2).
Tab. 1. Correlation between type 2 diabetes gene association scores and potential gene score confounders. 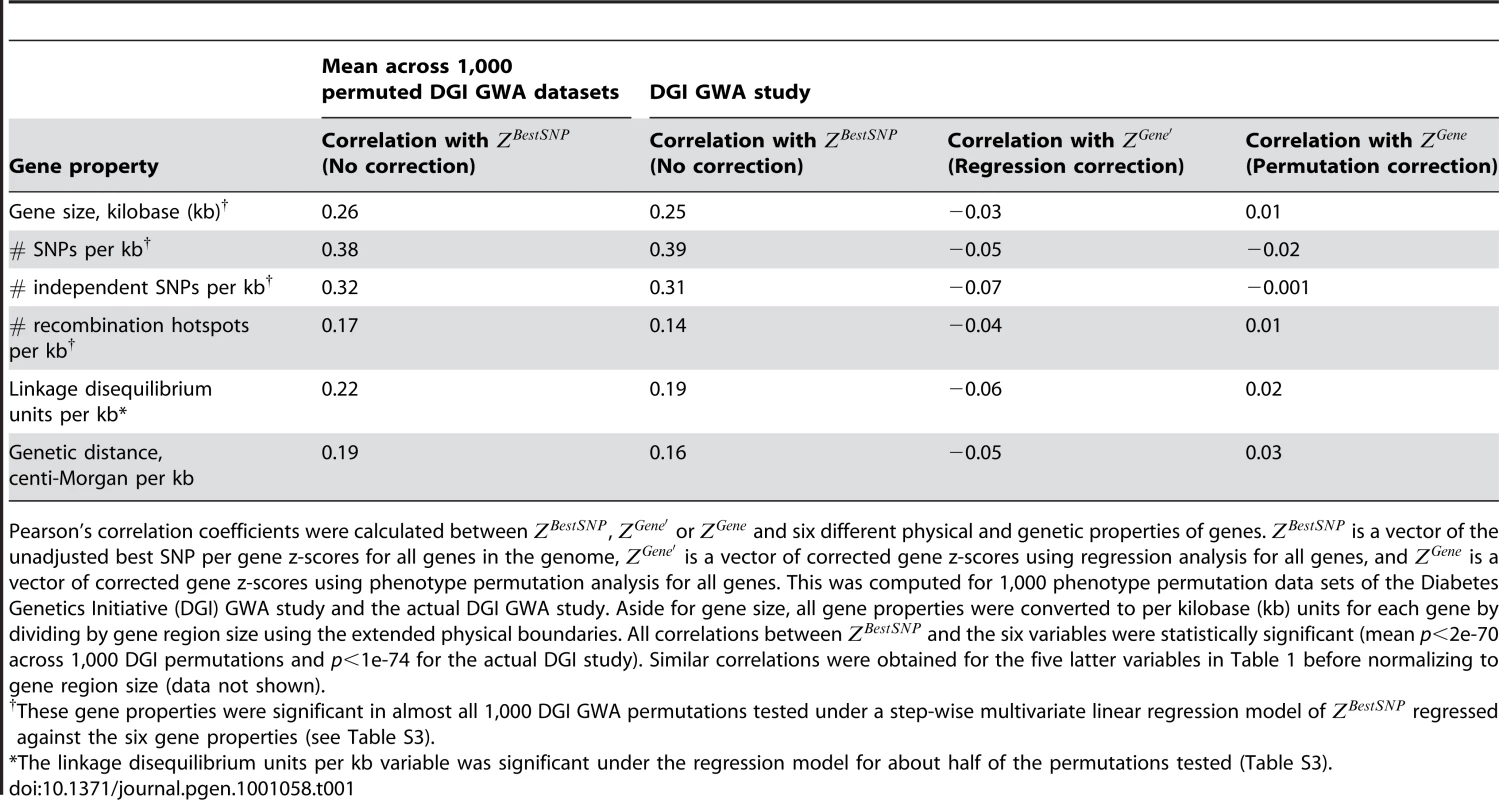
Pearson's correlation coefficients were calculated between , or and six different physical and genetic properties of genes. is a vector of the unadjusted best SNP per gene z-scores for all genes in the genome, is a vector of corrected gene z-scores using regression analysis for all genes, and is a vector of corrected gene z-scores using phenotype permutation analysis for all genes. This was computed for 1,000 phenotype permutation data sets of the Diabetes Genetics Initiative (DGI) GWA study and the actual DGI GWA study. Aside for gene size, all gene properties were converted to per kilobase (kb) units for each gene by dividing by gene region size using the extended physical boundaries. All correlations between and the six variables were statistically significant (mean p<2e-70 across 1,000 DGI permutations and p<1e-74 for the actual DGI study). Similar correlations were obtained for the five latter variables in Table 1 before normalizing to gene region size (data not shown). Having identified six potential gene score confounders, we used step-wise multivariate linear regression to remove these confounding effects from , to generate a corrected gene score, (see Materials and Methods and Figure 1C). In this analysis the confounders are removed sequentially, accounting for the correlations between the various gene properties. Aside from the genetic distance, all five remaining properties listed in Table 1 were significant under the step-wise linear regression model (p<0.05) applied to in either about half or all of the 1,000 permuted DGI data sets (Table S3). As a result the first five properties listed in Table 1 were used for subsequent analyses (see Table S4 for model coefficients and p-values for the DGI study and the DIAGRAM+ T2D meta-analysis).
The effectiveness of this approach was confirmed by comparing the DGI gene scores corrected with step-wise regression analysis to the corresponding gene scores corrected with traditional permutation analysis, as the latter corrects for all confounding effects (Figure 2; see Materials and Methods). The high correlation between the regression-corrected gene scores, and the permutation-corrected gene scores, for all genes (Pearson's correlation coefficients, r = 0.95; p<1e-30, Figure 2B) compared to before correction (r = 0.69, Figure 2A) indicates that only a small fraction of the confounding effects on is not explained by our regression method. Similar results were obtained when gene score ranks were compared (r = 0.95 versus r = 0.82; p<1e-30). A comparison of the distributions of for different sized genes using the permuted DGI data sets, demonstrates that the regression-based correction has indeed removed the confounding effect of gene size on (Figure S2).
Fig. 2. Regression analysis corrects for majority of confounding effects on gene association scores in a genotype-independent manner. 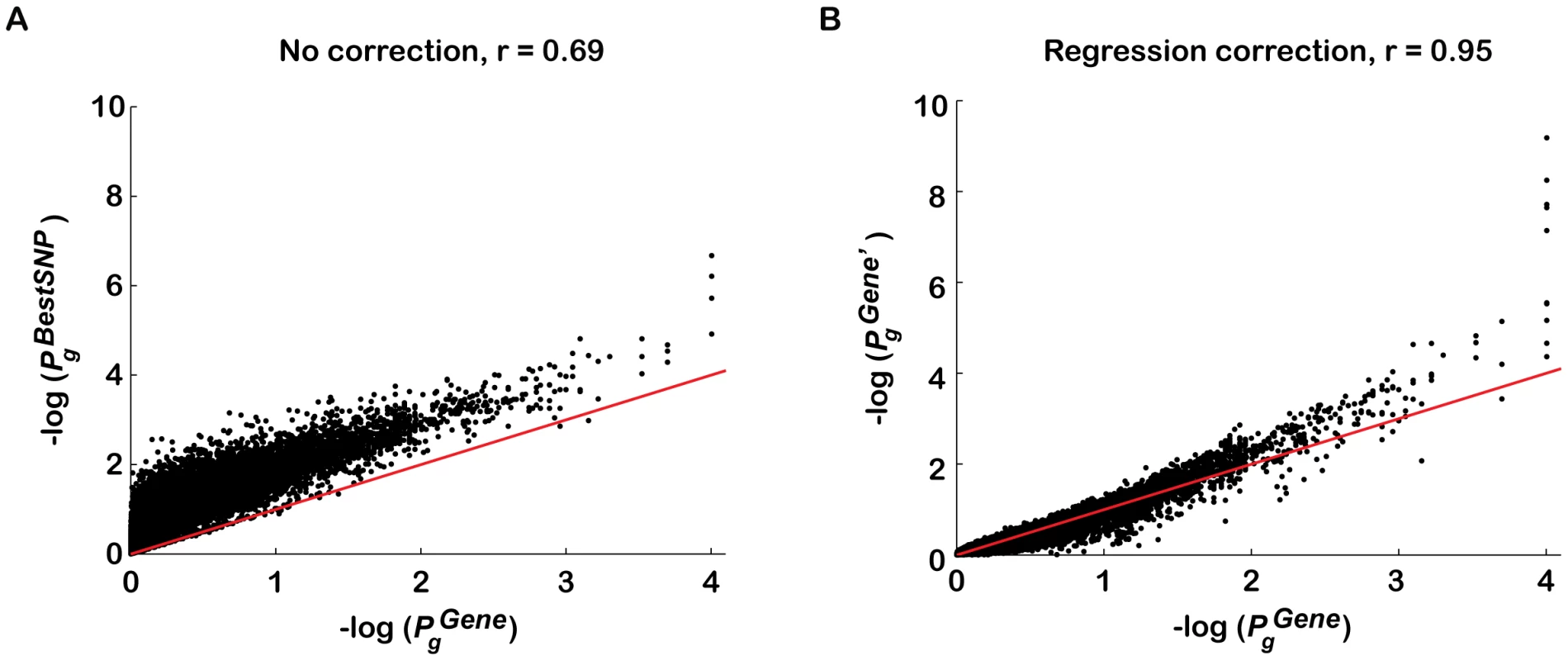
The performance of a step-wise regression analysis approach in correcting for confounders on was evaluated against permutation analysis correction, since the latter corrects for all confounders without requiring a priori knowledge of them. T2D gene association p-values were plotted for all genes g in the genome (A) before gene score adjustment () and (B) after correction for confounders using regression analysis (), as a function of corrected gene p-values using phenotype permutation analysis (). The Diabetes Genetics Initiative (DGI) GWA study was used for the analysis, since we had access to all individuals' genotypes. is the association p-value of the best regional SNP for gene g before correction (y-axis in A). To compute (y-axis in B), step-wise multivariate linear regression analysis was applied to against the first four confounders listed in Table 1 (this approach does not require genotype data). The Pearson's correlation coefficient (calculated between p-value vectors before log transformation) increased significantly following the regression-based correction (from r = 0.69 to r = 0.95). The spread around the diagonal (red line) also decreased following the regression correction (from a coefficient of variation (mean/std) of 1.13 to 0.56). The minimum is 10−4 as the p-values were calculated based on 1,000 permutations for genes with , and 10,000 permutations for genes with . Some of the variation in the low p-value tail is due to having done only 10,000 permutations (), and some to limitations of the linear regression method. Note that the four dots in (A) with contain ten overlapping dots that refer to four sets of 2–3 genes, each set assigned the same . Gene association p-values are plotted on a −log10(p-value) scale. We next compared the performance of the regression-based correction to an analytical method previously proposed to correct for the difference in number of (genotyped or imputed) SNPs per gene (Sidak's correction, [26], [39]). The Sidak correction did not perform as well as the regression-based correction (correlation with permutation-corrected gene p-values: r = 0.94, p<1e-30, but most gene p-values lie below diagonal; see Figure S3 for details). This is probably due to the method's assumption of independence between all SNPs in a gene region (eq. 4 in Materials and Methods). We then tested a modification of Sidak's correction proposed by Saccone et al. [40], which assumes that about 50% of all SNPs in a given chromosomal region are in high linkage disequilibrium (eq. 5 in Materials and Methods). This correction was comparable to, or slightly better than the regression method in the DGI test case (correlation with permutation-corrected gene p-values: r = 0.97, p<1e-30; Figure S3). These results are in concordance with our findings that number or density of SNPs is a dominant confounder on the best SNP per gene score, (Table 1), and that correcting for linkage disequilibrium between SNPs is necessary.
For the current study we used the regression-based correction, as it seems to behave equally well for different GWA studies (e.g. DGI study and DIAGRAM+ meta-analysis; see Figure S4A, S4B), while the modified Sidak's correction (in particular its correction for dependency between SNPs) may need to be adjusted for specific studies, e.g. due to different SNP densities (see Figure S4C, S4D). In any case, we later show that all GSEA results presented in this work are robust relative to the correction method used.
From genes to gene sets: estimating power of MAGENTA using simulations
After correcting for the majority of confounding effects on gene association scores, we next combined gene scores at the level of gene sets. We developed an approach similar to GSEA that tests whether predefined sets of functionally related genes are enriched for genes associated with a given complex disease or phenotype, more than would be expected by chance (Figure 1D). Specifically, the GSEA algorithm in MAGENTA tests for over-representation of genes in a given gene set above a predetermined gene score rank cutoff. The enrichment is evaluated against a null distribution of gene sets of identical set size that are randomly sampled from the genome multiple times (see Materials and Methods for details). The 95th percentile of all gene scores for a given GWA study or meta-analysis was used here as the enrichment cutoff (see Figure S5 for cutoff choice). Since subsets of genes in biological pathways are often physically proximal in the genome [25], for each gene set, we removed all but one gene from each subset of genes assigned the same best SNP, to prevent inflation of an enrichment signal due to positional clustering of genes (assuming one gene per associated variant).
We first evaluated the power (sensitivity) of the method to identify enrichment of modest associations. We considered models in which there is low detection power with single SNP analysis. We varied as parameters gene set size, fraction of genes in the set assigned a causal SNP (referred to as causal genes), effect size of the causal SNPs, and total number of causal genes. We performed multiple computer simulations where small effect sizes were randomly assigned to SNPs near different fractions of genes in a given gene set, against a background of randomized DGI for all SNPs i. Power was estimated for a given set of parameters as the fraction of simulation runs in which gene set enrichment was detected (described in Materials and Methods).
Figure 3 shows how the power of MAGENTA increases proportionately with the fraction (Figure 3A) or number (Figure 3B) of causal genes in three different gene set sizes, for a set of parameters chosen to be consistent with the lower bound effect size found to date in T2D and glycemic traits studied herein. For a given number of causal genes, small gene sets are more powerful; for a given fraction of causal genes, big gene sets have more power. Furthermore, as may be expected, power increases with the associated SNP effect size, and decreases with the total number of causal genes in the genome (Figure S6).
Fig. 3. Estimating power of the GSEA algorithm in MAGENTA using computer simulations. 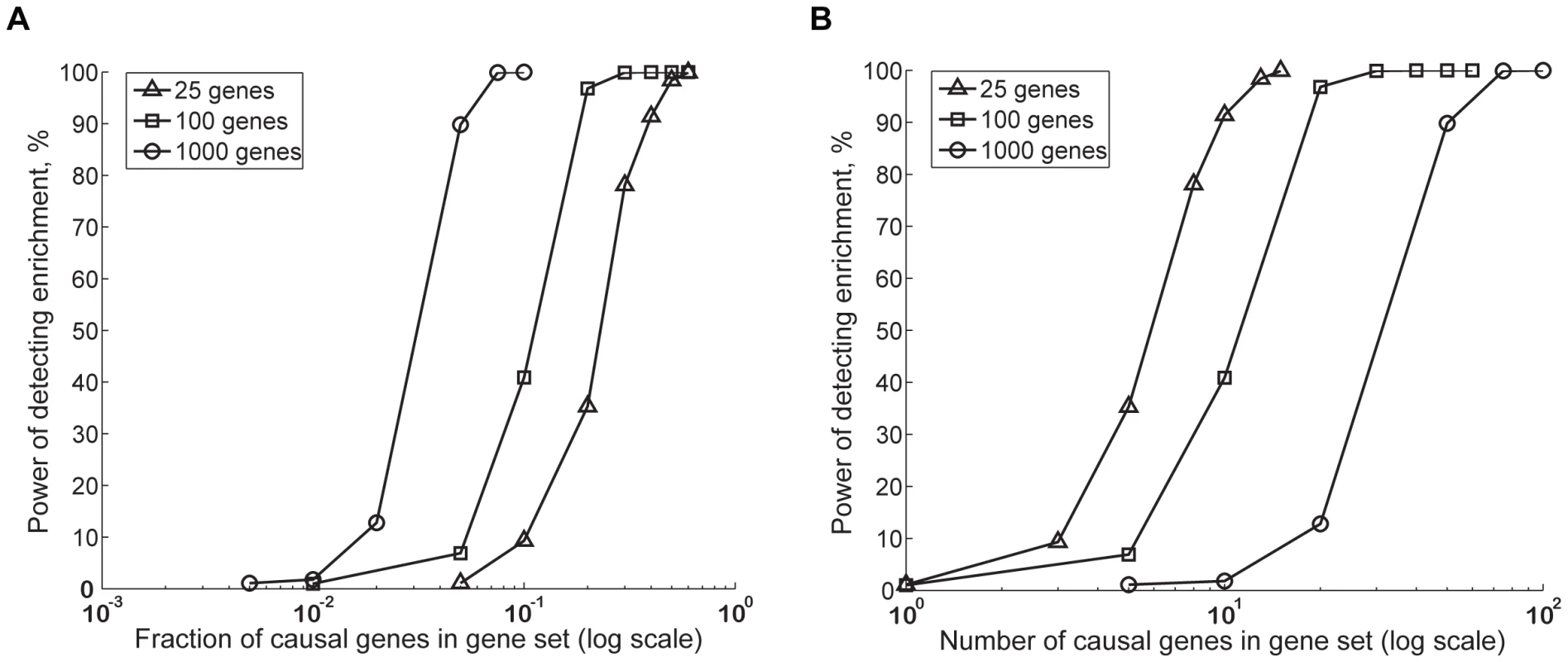
We used simulations to assess the power (sensitivity) of the gene set enrichment analysis (GSEA) algorithm in MAGENTA to detect enrichment of genes with modest effect sizes that are hard to detect with single SNP analysis. Power is plotted as a function of fraction (A) or number (B) of causal genes of modest effect in gene sets of 25 (triangles), 100 (squares), or 1,000 (circles) genes. The modest effect size spiked into genes is equivalent to 1% power of detecting an association at genome-wide significance using single SNP analysis. A total of 100 causal genes in the genome were assumed here. Randomized vectors from case/control permutations of the DGI study were used as the background association values. Simulations were repeated 1,000 times for each unique set of parameters. Power was calculated as the fraction of times the simulated gene set received a <0.01. For specificity estimations we used SNPs with no effect size, sampled from a null distribution that assumes no association. The false positive rate of the method (1-specificity) was comparable to the p-value cutoff used (0.3–1.7%). Note the x-axis in both panels is on a log10 scale. Our simulations identified scenarios under which analysis of GWA SNP data at the level of gene sets adds power in detecting associations of small effect (e.g. odds ratio of 1.07 for an allele frequency of 0.2–0.3 and sample size of 10,000 individuals [41]) compared to single SNP analysis. For example, consider a total of 100 causal genes in the genome each with an effect size, sufficient to provide 1% power of detecting an association at the individual SNP level at genome-wide significance. In this setting, MAGENTA has 50% power of detecting enrichment if a given set of 1,000 genes (e.g. nuclear-encoded mitochondrial genes) contains ∼3% or 30 genes with a modest effect, when 100 genes (e.g. OXPHOS genes) contain ∼10% or 10 genes with a modest effect, or when 25 genes (e.g. on the order of the number of nuclear regulators of mitochondrial genes) contain ∼25% or 6 genes with a modest effect.
Validation of MAGENTA on lipoprotein and lipid GWA study meta-analyses
We next tested empirically the performance of MAGENTA on LDL cholesterol, HDL cholesterol and triglyceride blood levels. The molecular pathways involved in lipid and lipoprotein metabolism are relatively well known, and many of the genes that lie near the 30 SNPs so far reported to be associated with one or more of these traits function in known processes related to lipid or lipoprotein metabolism [34]. MAGENTA was applied to three GWA meta-analyses [34], whose sample size (19,840 individuals) is on the same order of magnitude as that of the largest available T2D meta-analysis (DIAGRAM+) used below to test for mitochondria-related associations with T2D. A total of 51 (partially overlapping) gene sets related to lipid, lipoprotein and fatty acid metabolism were tested (defined by PANTHER [42] and Gene Ontology [43] databases; see Materials and Methods). Of these gene sets, we found biological processes related to lipid, lipoprotein and fatty acid metabolism, binding and transport activities, and triglyceride metabolism to be significantly enriched for LDL cholesterol, HDL cholesterol and/or triglyceride associations after Bonferroni correction (top gene sets are listed in Table 2; full list in Tables S5, S6, S7). These results are robust relative to the method used to correct for confounders on gene association scores (Tables S8, S9, S10). Enrichment of LDL and HDL associations in the lipid transport process has been previously reported [25]. While most of the enriched processes contain at least one gene near a validated lipid SNP, this analysis also found enrichment in a pathway with unknown associations (the fatty acid metabolic process). The fact that the enrichment signals for many of the significant processes were still detectable after removing the known lipid genes from the GSEA analysis, suggests that some of the nominally significant associations in these pathways may represent true associations of more modest effects yet to be identified.
Tab. 2. Top GSEA results for lipid-related pathways using LDL cholesterol, HDL cholesterol, and triglyceride GWA meta-analyses. 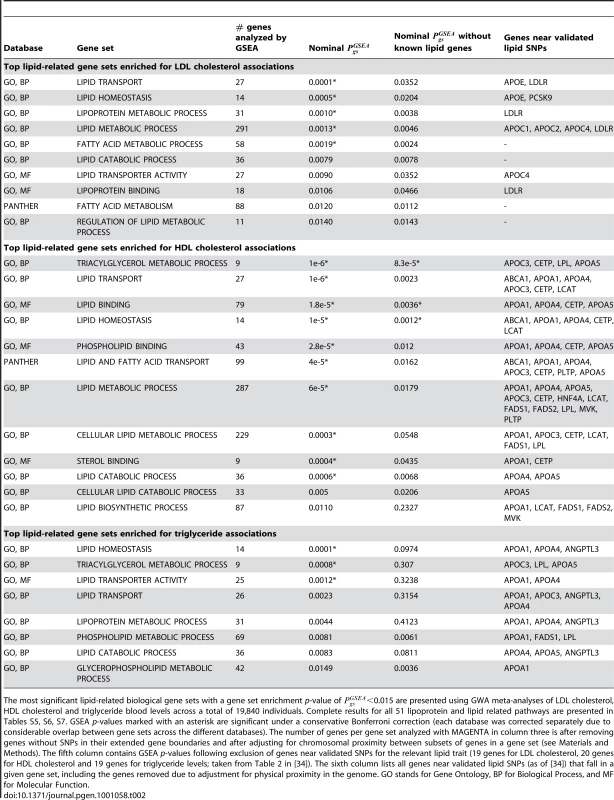
The most significant lipid-related biological gene sets with a gene set enrichment p-value of <0.015 are presented using GWA meta-analyses of LDL cholesterol, HDL cholesterol and triglyceride blood levels across a total of 19,840 individuals. Complete results for all 51 lipoprotein and lipid related pathways are presented in Tables S5, S6, S7. GSEA p-values marked with an asterisk are significant under a conservative Bonferroni correction (each database was corrected separately due to considerable overlap between gene sets across the different databases). The number of genes per gene set analyzed with MAGENTA in column three is after removing genes without SNPs in their extended gene boundaries and after adjusting for chromosomal proximity between subsets of genes in a gene set (see Materials and Methods). The fifth column contains GSEA p-values following exclusion of genes near validated SNPs for the relevant lipid trait (19 genes for LDL cholesterol, 20 genes for HDL cholesterol and 19 genes for triglyceride levels; taken from Table 2 in [34]). The sixth column lists all genes near validated lipid SNPs (as of [34]) that fall in a given gene set, including the genes removed due to adjustment for physical proximity in the genome. GO stands for Gene Ontology, BP for Biological Process, and MF for Molecular Function. Gene set enrichment analysis of T2D associations in mitochondria-related gene sets
Having validated the utility of MAGENTA, we next used the method to test whether mitochondria-related gene sets are enriched for multiple genes that lie near common variants with modest effects on T2D susceptibility. We tested three molecular hypotheses based on the observations of reduced OXPHOS activity and expression levels and fewer and smaller mitochondria in diabetic muscle (described in the Introduction). The three hypotheses were: DNA variants that alter the function of different nuclear regulators of the OXPHOS pathway and/or other mitochondrial processes are associated with T2D, variants that cause core defects in OXPHOS activity that may result in compensatory alterations of OXPHOS levels are associated with T2D, and variants that affect other mitochondrial functions in addition to the OXPHOS process are associated with T2D. To test these hypotheses, we tested for enrichment of T2D associations in the following three gene sets: a set of known nuclear regulators of mitochondrial genes, the OXPHOS genes, and all known nuclear-encoded mitochondrial genes. In parallel to testing the relevance of these three sets to T2D, we explored their possible associations (in non-diabetic individuals) with seven specific glycemic traits that are risk factors for T2D (listed below).
We first analyzed a set of 16 nuclear regulators of mitochondrial genes assembled based on the literature (listed in Table S11) [35], [44]–[48], using the latest DIAGRAM+ T2D GWA meta-analysis of 8,130 cases and 38,987 controls from eight GWA studies [36]. Since no individual mitochondria regulator was found to date to be significantly associated with T2D at genome-wide significance, we tested the hypothesis that common variants in more than one regulator may affect T2D risk (possibly through OXPHOS downregulation) in the diabetic populations analyzed here. Upon applying MAGENTA to the set of nuclear regulators we did not observe significant enrichment of T2D associations compared to the genomic background of gene scores (Table 3; = 0.19; Quantile-quantile plot of gene p-values in Figure S7A). The peroxisome proliferator-activated receptor delta, PPARD (Entrez ID 5467) [44], received the best T2D gene p-value, although it was not gene-wide significant ( = 0.0089). The gene scores of the 16 known nuclear regulators of mitochondrial functions are listed in Table S11.
Tab. 3. Mitochondria-related gene sets are not enriched for associations with type 2 diabetes. 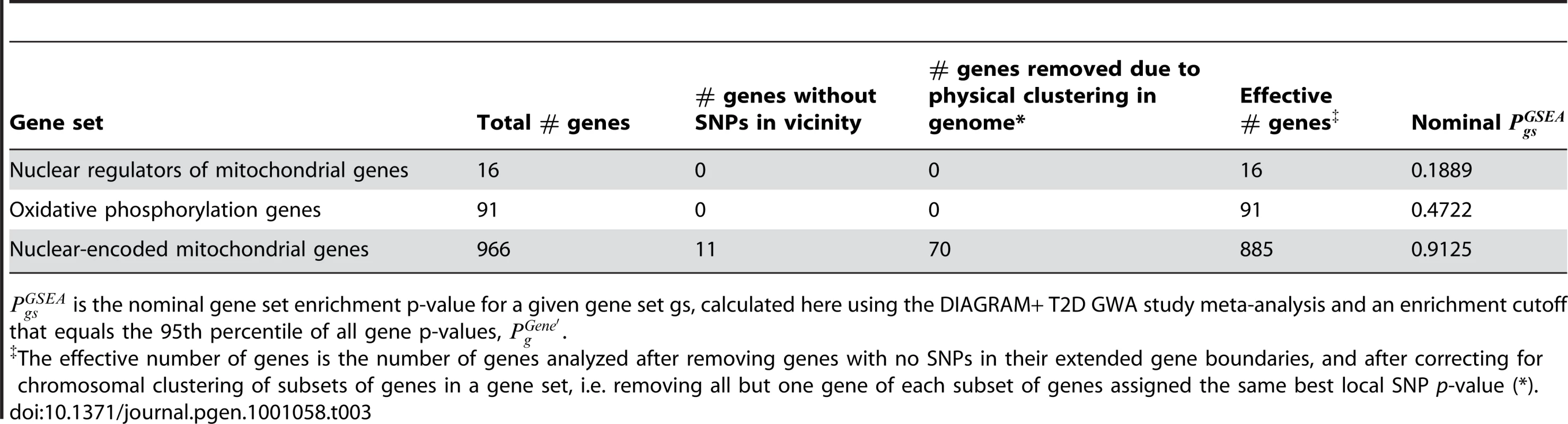
is the nominal gene set enrichment p-value for a given gene set gs, calculated here using the DIAGRAM+ T2D GWA study meta-analysis and an enrichment cutoff that equals the 95th percentile of all gene p-values, . Next, we tested for enrichment of T2D associations in a set of 91 autosomal OXPHOS genes (highlighted in the full list of mitochondrial gene scores in Table S12). Using MAGENTA, no significant enrichment of T2D associations was found among the 91 OXPHOS genes analyzed (Table 3; = 0.47). A plot of the OXPHOS T2D gene scores against an expected distribution of gene scores is shown in Figure S7B.
Finally, we applied MAGENTA to 966 nuclear-encoded human mitochondrial genes taken from the MitoCarta compendium (∼85% of all mitochondrial genes; see Materials and Methods) [22]. We did not observe significant enrichment of T2D associations for the whole set of mitochondrial genes either (Table 3; nominal = 0.91). A more detailed view of the mitochondrial gene score distribution is shown in Figure S7C (see Table S12 for a list of all mitochondrial gene association p-values).
While the above findings show no evidence of association between relevant mitochondrial gene sets and T2D, these genes could still display causal associations with specific intermediate phenotypes linked to the disease. Support for this comes from reported mitochondrial dysfunction in insulin-resistant individuals [8]. Therefore, we tested the same three gene sets described above for enrichment of associations with seven different glucose and insulin-related traits characteristic of T2D, using GWA meta-analyses of up to 46,186 non-diabetic individuals [37], [38] (Soranzo N. et al., unpublished data). The quantitative traits analyzed include fasting levels of glucose and insulin, glucose and insulin levels 2 hours following a 75-gram oral glucose tolerance test, indices of β-cell function (HOMA-B) and insulin resistance (HOMA-IR) [49], and glycated hemoglobin levels (HbA1C), which reflect long-term plasma glucose concentrations (see Materials and Methods).
No significant enrichment of genes associated with either of the seven glycemic traits tested was observed for the set of nuclear regulators of mitochondrial genes, the OXPHOS genes or the full set of nuclear-encoded mitochondrial genes, after correcting for multiple hypothesis testing (Table 4). Similar results were obtained between all three gene sets and T2D or the seven glycemic traits tested, using an alternative GSEA statistical test based on a rank-sum test (see Materials and Methods and Table S13) or using an alternative gene score correction method (modified Sidak's correction; Table S14), confirming the robustness of these results.
Tab. 4. Mitochondria-related gene sets are not enriched for associations with type 2 diabetes-related glycemic traits. 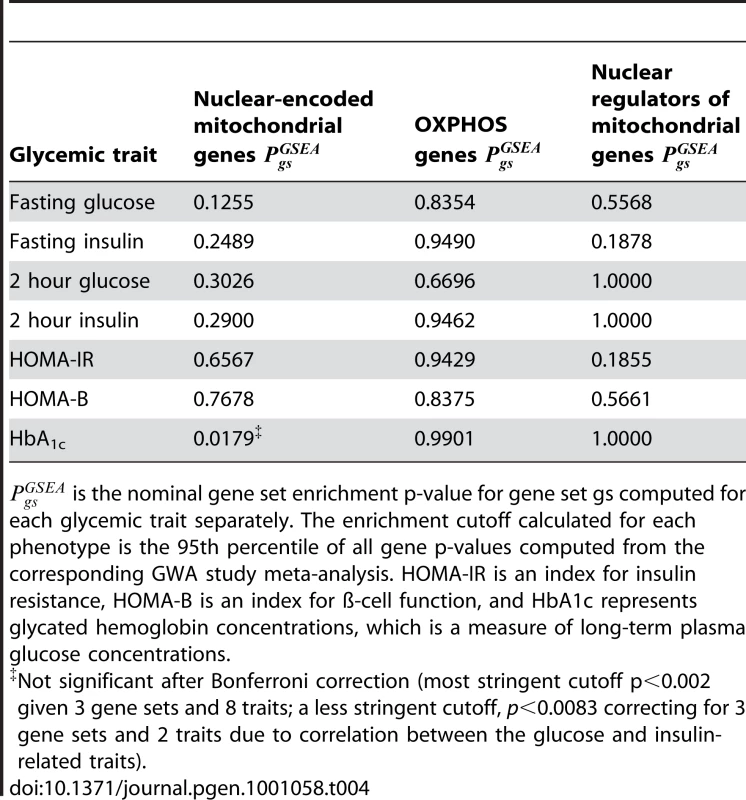
is the nominal gene set enrichment p-value for gene set gs computed for each glycemic trait separately. The enrichment cutoff calculated for each phenotype is the 95th percentile of all gene p-values computed from the corresponding GWA study meta-analysis. HOMA-IR is an index for insulin resistance, HOMA-B is an index for ß-cell function, and HbA1c represents glycated hemoglobin concentrations, which is a measure of long-term plasma glucose concentrations. In summary, our gene set analysis of T2D and glycemic traits did not provide support for many weak mitochondria-related associations.
Discussion
We tested the open question of whether mitochondrial dysfunction is a primary cause of type 2 diabetes (T2D) as opposed to a secondary cause or an outcome of the disease. Using a genetic approach, we comprehensively analyzed common variant associations at the level of genes and gene sets, in search for multiple modest genetic effects on T2D pathogenesis in a set of nuclear regulators of mitochondrial activity, the oxidative phosphorylation (OXPHOS) genes, or the full known set of ∼1,000 nuclear-encoded mitochondrial genes (an estimated 85% of all mitochondrial genes). For this analysis, we developed a modified GSEA approach applied to genetic association data (p-values or z-scores), which we named MAGENTA. MAGENTA was especially designed to exploit the increased power of meta-analyses of multiple GWA studies. In the process we identified and adjusted for confounders on gene scores and gene set enrichment scores in the absence of genotype information. This method was rigorously tested and evaluated using real and simulated GWA data, and we demonstrate realistic scenarios in which this approach could identify significant set-wide association signal that is likely to be overlooked in individual SNP analysis.
Identifying and correcting for confounders on SNP to gene association p-values
In testing for possible confounding effects, we observed that the unadjusted most significant SNP per gene p-value is affected by several gene properties, most notably physical gene size and number or density of SNPs per gene, and the genetic properties: number or density of SNPs across a gene that are in linkage equilibrium to each other and number or density of recombination hotspots that span a gene. While gene size and number of SNPs per gene have been recently reported to be correlated with the unadjusted best SNP p-value [23], [25], [33], we have quantitatively demonstrated the magnitude of these and linkage-based effects using randomized GWA study data, confirming their potential confounding effects. We show that large genes tend to receive a more significant score than small genes by chance (Figure S2).
By using regression analysis to adjust the gene scores for the confounding effects we identified, we provide a viable approach to determine gene association p-values in the absence of genotype data, which should prove useful for mining large GWA study meta-analyses or other types of GWA studies where only variant association statistics are available. Using the Diabetes Genetics Initiative (DGI) study, we showed that our correction accounts for most of the confounding effects on the most significant SNP score and yields gene scores that are much more accurate than those obtained without correction [31]. Notably, this regression approach and the DGI permutation system can be used to identify and adjust for confounders on other types of SNP to gene scores (e.g. considering best SNP per LD block [25], [33] or the set–based test in PLINK http://pngu.mgh.harvard.edu/~purcell/plink/anal.shtml#set). While in the current work we focus largely on developing a gene set approach following gene score correction, we envisage that the corrected gene p-values might be valuable in future gene-centric studies, allowing one to properly weigh specific genes (e.g. small genes) that may otherwise be missed.
Power of MAGENTA evaluated using simulated and true association data
Using computer simulations, we show that MAGENTA has considerable power (i.e. sensitivity) in detecting multiple modest effects relative to traditional single SNP analysis for a range of parameters. For example, for a gene set size of 100 genes, our method has 50% power of detecting enrichment when ∼10 genes have weak effects (that are equivalent to 1% detection power at single SNP level) versus 10% power of detecting only one of the 10 genes in single SNP analysis. By applying MAGENTA to GWA scan meta-analyses for LDL cholesterol, HDL cholesterol and triglyceride levels, we confirmed the method's ability to pick out relevant biological processes. We note that the nominal MAGENTA p-values for these positive controls were not exceedingly low (on the order of 10−2 to 10−6), emphasizing the limited power of the gene set approach. Our simulations allowed us to provide quantitative estimates of these limitations, and indications of possible limiting factors. For example, we found that power levels increase considerably with gene set size, fraction of causal genes in a gene set, and effect size of associated SNPs, and decrease with total number of causal genes in the genome. Similar trends, as a function of effect size and fraction of causal SNPs, have been shown with other types of GSEA methods that test for enrichment in SNP sets across pathways [32], [33].
No evidence for a causal role of mitochondrial dysfunction in T2D
Despite a large sample size, comprehensive gene lists, and a calibrated statistical method, we did not find evidence that common variants in proximity to ∼1,000 known nuclear-encoded mitochondrial genes contribute to T2D susceptibility. Similarly, we found no indication of significant associations between variants near these genes and intermediate physiological phenotypes related to T2D. Simulations of MAGENTA performance suggest that if there is a genetic contribution it is small - probably no more than 2–4% of nuclear-encoded mitochondrial genes (∼20–40 genes) harbor common variants of modest effect (e.g. an odds ratio of ∼1.07 for allele frequency of 0.2–0.3 and sample size of 10,000 individuals) on T2D risk. This number may vary to some extent depending on the actual effect sizes and total number of causal genes for the disease (see Figure S6). As of the latest T2D meta-analysis used here (DIAGRAM+), three mitochondrial genes (IDE, C8orf38 (Entrez ID 137682), and ACADS (Entrez ID 35)) lie near validated T2D SNPs amongst other genes in the interval [20], but a causal connection for these genes with T2D has not yet been shown.
Although the expression of multiple OXPHOS genes is downregulated in skeletal muscle of patients with diabetes [9], and OXPHOS activity is reduced in diabetic and insulin-resistant individuals, we did not find evidence that OXPHOS genes lie near genetic variants that affect T2D risk or related glycemic traits. This is consistent with a previously reported pathway analysis of one of the T2D GWA studies included in the DIAGRAM+ meta-analysis [27]. Lack of enrichment in the OXPHOS genes suggests that either the changes in expression are an effect and not a cause of diabetes, or that one or few regulators of OXPHOS [35] contain yet undetected rare or common variants, or inherited epigenetic changes associated with T2D or a related phenotype. Since, to date, there is no conclusive evidence for a strong association of any of the 16 known nuclear regulators of mitochondrial genes to T2D, we tested whether several regulators might harbor common variants with modest effect on T2D risk in the population. In our analysis we could not find strong support for this possibility. Our simulations suggest that we would have considerable power to detect enrichment if at least ∼9 OXPHOS genes or at least ∼3 nuclear regulators were modestly associated with T2D or a related trait. While specific genes ranked high among the 16 regulators (but not at gene-wide significance), such as GABPA (the GA binding protein transcription factor, alpha subunit) [50] with respect to T2D associations or SIRT1 (sirtuin, silent mating type information regulation 2 homolog 1; Entrez ID 23411) [51], [52] with respect to fasting insulin levels and measures of insulin resistance and ß-cell function, our statistical tests do not constitute a proof of their involvement in T2D. Future gene-centric approaches using our corrected gene scoring system or others may be used to examine more closely these and similar instances.
We note that while lack of enrichment of associations with T2D and related-traits does not provide support for a causal connection, it does not eliminate the possibility that individual genes could still be found to have a genetic effect and thus be instrumental to T2D predisposition. For example, the absence of enrichment in the OXPHOS genes does not disprove the association to T2D of one of its genes, C8orf38 (an assembly factor in Complex I, the first complex in the mitochondrial electron transfer chain; Entrez ID 137682) [22], which lies near a validated T2D SNP found in the recent DIAGRAM+ T2D meta-analysis [36], but it does not provide further support for C8orf38 being causal.
Limitations of MAGENTA and other GSEA approaches applied to variant association data
Our finding that specific mitochondria-related gene sets functionally implicated in T2D are not enriched for associations could be due to several reasons, of potential relevance also to the study of other diseases: (i) The fraction of causal genes in the given gene set, while considerable, may not be significantly higher than the total fraction of causal genes in the genome (especially relevant to gene permutation analysis); (ii) The causal variants may be spread across a large number of biological processes or there may be allelic heterogeneity in the population, making it hard to detect clustering of associations into pathways; (iii) Causal genes for certain phenotypes may cluster in small pathways, which are more sensitive to individual gene score fluctuations than large pathways; (iv) The relevant pathways or sets of functionally related genes may have not yet been tested; (v) By considering only variants within a given distance around each gene, potential signals from more distant transcriptional regulatory elements, such as enhancers or epigenetic marks, might be missed; future genome-wide maps of regulatory elements may be used to generate a discontinuous and precise map of potential causal regions per gene; and finally (vi) Rare variants were not tested, but when the data are available the MAGENTA framework can be applied to this class of variants.
General applications of MAGENTA and other GSEA approaches to GWA studies
Certain common diseases and traits may be more amenable to GSEA approaches than others, depending on their genetic architecture. In addition to identifying new biological pathways or processes associated with disease risk or trait variation, GSEA methods, such as MAGENTA, may provide predictions for new disease or trait genes of modest effects (top ranked gene scores in enriched gene sets). Such joint analysis of SNPs (or other types of variants) at the gene and gene set levels should be most useful for detecting associations in a narrow range of nominal significance levels (between noise levels, e.g. p<0.1, and SNP replication cutoff, e.g. p>∼0.0001), a range that has been shown to contain associations of small effect in polygenic disorders [53]. The GSEA approach may also help prioritize potential causal genes in validated association regions that contain multiple genes.
Our method which explicitly accounts for important confounders on the association scores of genes (e.g. gene size) and gene sets (e.g. positional effects of genes in a gene set) in the absence of genotype data, and that provides upper-bound estimates of number of associations per gene set, should provide accurate tests of gene sets of interest, especially for analyzing large GWA scan meta-analyses. MAGENTA can also be applied to sets of genetic loci other than genes, such as linkage disequilibrium blocks. More generally, such GSEA approaches may be valuable for gene and pathway analysis of other types of genetic studies that deal with multiple measurements per gene, such as exon resequencing in case-control studies.
Materials and Methods
Ethics statement
The study constitutes a secondary analysis of genetic data derived from de-identified samples, and thus has an IRB exemption.
GWA studies and meta-analyses analyzed
Two type 2 diabetes (T2D) GWA studies were analyzed in this work. The first is the Diabetes Genetics Initiative (DGI) GWA study, used for method development purposes. 381,099 genotyped SNPs were analyzed using only the population-based individuals, that consist of 1,022 diabetic patients and 1,075 matched control individuals (a total of 2,097 individuals) [17]. The second study is the most recent T2D GWA meta-analysis (DIAGRAM+) [36], used to test the mitochondrial-diabetes hypothesis with MAGENTA. The meta-analysis was performed across eight GWA studies, with a total of 8,130 diabetic patients and 38,987 non-diabetic controls (47,117 individuals total, effective sample size n = 22,044), and 2,255,856 genotyped and imputed autosomal SNPs.
The GWA study meta-analyses of seven diabetes-related glycemic traits analyzed in this work were part of the Meta-Analyses of Glucose and Insulin-related traits Consortium (MAGIC) [37], [38] (Soranzo N. et al., unpublished data). These seven traits include fasting glucose concentrations, fasting insulin concentrations, 2-hour glucose and 2-hour insulin concentrations after an oral glucose tolerance test, indices of β-cell function (HOMA-B) and of insulin resistance (HOMA-IR), calculated from fasting glucose and insulin measures using homeostasis model assessment [49], and HbA1C (glycated hemoglobin) levels. The meta-analyses for fasting glucose, fasting insulin, HOMA-B and HOMA-IR were performed on 20 or 21 GWA studies with a total of 36,466 to 46,186 non-diabetic individuals [37], [38], the meta-analyses for 2-hour glucose and 2-hour insulin were performed across 9 studies and a total of 15,234 individuals [37], [38], and the meta-analysis for HbA1C was performed across 23 cohorts with a total of 35,920 non-diabetic individuals (Soranzo N. et al., unpublished data). The total number of genotyped and imputed autosomal SNPs analyzed in these seven meta-analyses varied between 2,323,569 and 2,748,910 SNPs.
To test the performance of MAGENTA on traits whose underlying biology has been well studied, we analyzed three GWA study meta-analyses of low-density lipoprotein (LDL) cholesterol, high-density lipoprotein (HDL) cholesterol and triglyceride blood levels [34]. All three meta-analyses were performed with 19,840 individuals from seven GWA studies, on 2,552,754, 2,552,580 and 2,552,773 genotyped and imputed SNPs for the LDL cholesterol, HDL cholesterol and triglyceride meta-analyses, respectively.
The association tests of all the aforementioned GWA studies were performed at the single SNP level, assuming an additive allelic model. The individuals in all GWA studies are of European descent.
Meta-Analysis Gene-set Enrichment of variaNT Associations (MAGENTA)
Step 1: Mapping SNPs onto genes
A list of 26,914 human gene transcripts was downloaded from the UCSC Genome Browser (http://genome.ucsc.edu/) in RefFlat format based on the human March 2006 (hg18) assembly. In the current study, 18,434 unique genes were used (17,680 on autosomes, and 754 on sex chromosomes), after filtering out genes with two or more transcripts that lie more than 1Mb apart on the same chromosome or that lie on separate chromosomes. All the genotyped or imputed SNPs that lie within an added physical distance upstream or downstream to a gene's most extreme transcript start and end sites of all its known splicing isoforms (intron and other non-coding sequences included) were assigned to each of the 18,434 genes. For gene set enrichment analysis of T2D, glycemic traits, and lipid and lipoprotein traits we used 110 kb upstream to the gene's most extreme transcript start site and 40 kb downstream to the gene's most extreme transcript end site. These boundaries were chosen as they represent the 99th percentile of the distances of cis-eQTLs from their adjacent gene's transcript start and end sites. This is according to a comprehensive genome-wide analysis of putative functional regulatory elements (cis-eQTLs) using expression data from human lymphoblastoid cell lines [54]. These boundaries were chosen in attempt to capture association signals from proximal regulatory regions, in addition to the coding region. For the analysis of the DGI GWA study and the DGI permutations (used for method development purposes), ±50 kb was used, as these analyses were done before the Veyrieras et al. publication [54]. In the future, when transcriptional elements are comprehensively characterized for all genes in the genome, a discontinuous and more precise map of regulatory regions for each gene could be used for assigning SNPs to genes.
Steps 2 and 3: Scoring genes based on SNP association scores and correcting for confounders
For each gene g in the genome we calculated a score, that is the probability that the gene is associated with a given disease or trait. In computing this score we corrected for the confounding effects of physical and genetic properties of genes on the gene p-value.
Step 2
The scoring metric used here is as follows: For each gene g, the minimum GWA p-value of all SNPs with index i that fall within the extended gene boundaries (see Step 1) is chosen, :(1)where I(g) is the set of indeces of SNPs whose chromosome positions fall between the extended gene boundaries. is the association p-value for SNP i calculated in a GWA study or meta-analysis (see GWA studies and meta-analyses section). A z-score is then computed based on for each gene g, using a mean of 0 and standard deviation of 1, assuming a normal distribution. should be most powerful for genes that contain one major target region or haplotype with potential causal mutations in or around their coding sequence. Other SNP to gene scoring metrics can be used here.
Step 3
To correct for confounding effects on we regressed out the effect of several potential confounders from , using step-wise multiple linear regression analysis [55]. The method begins by regressing out the effect of a variable with high correlation with the gene score; it then adds the next significant variable, and evaluates whether the added variable should be kept and whether any existing variables should be eliminated from the regression model. The latter step is repeated until all variables are considered. A variable was added at p<0.05 and removed at p>0.1. The step-wise nature of this method should account for correlations between the variables. We initially tested this model using 1,000 DGI GWA permutations and six gene properties as potential confounders (predictor variables). In this case, step-wise multivariate linear regression was applied to using the full list of genes, and the coefficients α, β, δ, γ, η, and were estimated such that for every gene g one can calculate:(2)where is the residual of the association score for gene g that cannot be explained by the effects of the predictor variables considered. After the regression a corrected gene z-score, can be written as follows:(3)A corrected gene p-value is calculated from assuming a normal distribution and a mean of 0 and standard deviation of 1 (reasonable approximation but not perfect, in particular for the less significant values of ; see Figure S8). Of all six gene properties tested, only the genetic distance, , was not significant (p>0.05) in most of the DGI permutations subjected to the regression analysis (Table S3), and hence was used for all analyses in this paper. Similar GSEA results were obtained for all gene sets and traits analyzed in this paper when only the first four variables listed in Table 1 (significant in almost all 1,000 DGI permutations tested; see Table S3) were used for the regression-based correction of gene scores ( and ) (data not shown).
This step-wise linear regression approach can be used to adjust for confounders on other types of variant to gene scoring metrics, and an appropriate set of potential confounders can be identified using the DGI permutation system described below.
Comparison to analytical gene score correction methods
The regression-based method was compared to Sidak's combination test, also known as Sidak's correction [26], and to a modified version of Sidak's correction [40]. The corrected gene p-value, based on Sidak's correction is defined as follows for gene g:(4)where , defined in eq. 1, is the most significant SNP p-value for gene g, and N is the total number of SNPs with available association statistics for gene g. A modification of eq. 4 proposed in [40] uses (N+1)/2 as the exponent to adjust for linkage disequilibrium between regional SNPs, assuming ∼50% of SNPs in a given genomic region are in tight linkage disequilibrium:(5)
Step 4: Gene set enrichment analysis of genome-wide association data
To test for over-representation of genes with modest genetic effects on a complex disease or trait in predefined sets of genes, we developed a gene set enrichment analysis (GSEA) algorithm that is applied to gene association p-values adjusted for confounding effects. This algorithm does not require the genotypes of individuals in the association scans in order to estimate gene set enrichment significance. Our GSEA test was inspired by the original GSEA algorithm applied to expression data [9], [24], more recently modified for SNP association data [23], [25], [28], [32], but uses a different statistical test. The null hypothesis is that the gene association score ranks of all genes with index g that belong to a given gene set gs are randomly distributed. The alternative hypothesis is that there is an over-representation in gene set gs of gene score ranks above a given rank cutoff compared to multiple random gene sets of identical size that were randomly sampled from all genes in the genome.
The specific steps of the GSEA statistical test employed here are as follows: (i) Corrected gene association p-values were calculated for all genes in the genome, based on a given GWA study or meta-analysis. In this study, we used the corrected gene p-value, as it can be computed for studies where individuals' genotypes are not available. If genotype data are available, the gene score can also be computed (see above for definition and section below for definition). (ii) Several types of genes were removed from gene sets. Genes with no SNPs in their extended gene boundaries were not included in the analysis. In addition, for each subset of genes in a given gene set that were assigned the same most significant SNP, all genes but one were removed from the analysis; the gene with the most significant gene score was retained. This was done to eliminate potential inflation of gene set enrichment significance due to two or more genes in a gene set that are physically proximal along the chromosome and hence may capture the same association signal (assuming one causal gene per associated locus). This yielded an effective number and set of genes that was used for the next steps of the GSEA test. (iii) For each gene set gs the fraction of genes with < was recorded (denoted here as the ‘leading edge fraction’), where is a predetermined gene p-value cutoff, defined as a given percentile of all gene p-values in the genome. is specific for a given GWA study or meta-analysis. In this study, we used = 95th percentile of for all genes g in the genome, as it gave the optimal power of five cutoffs tested (99th, 95th, 90th, 75th, and 50th percentile of all gene p-values) with power simulations (see Figure S5 and Simulations section below). (iv) Finally, a nominal GSEA p-value, was calculated for each gene set gs, defined as the fraction of randomly sampled gene sets of identical set size, whose leading edge fraction is equivalent to or larger than the observed leading edge fraction of gene set gs. The null distribution of leading edge fractions was generated for each gene set gs by randomly sampling 10,000 gene sets from the genome (or more when <10−4) that are of identical set size to the effective size of gene set gs (after adjusting for physical clustering in the genome of subsets of genes in each randomly sampled gene set separately, as described above). Genes in gene set gs were not excluded from the random sampling procedure. (v) To correct for multiple hypothesis testing, Bonferroni correction was used (i.e. significance cutoff p = 0.05 divided by the number of hypotheses tested). This may be too stringent when a large number of gene sets is tested due to overlap of genes between the different gene sets.
To test the robustness of our GSEA results for the mitochondria-related gene sets, we applied an alternative GSEA statistical test, based on a one-tailed Mann-Whitney rank-sum test (Table S13). First, for each gene set gs we calculated a one-tailed rank-sum p-value that tests the alternative hypothesis that ranks for all genes in gene set gs are skewed towards high ranks compared to the gene score ranks of the rest of the genes in the genome. Second, a similar one-tailed rank sum p-value was calculated for 10,000 random gene sets of identical size that were randomly sampled from the genome and adjusted for chromosome clustering of subsets of genes in the gene set. Finally, a rank-sum based GSEA p-value, was computed for gene set gs as the fraction of randomly sampled gene sets whose rank-sum p-value was equivalent to or more significant than the rank-sum p-value of the tested gene set gs.
Identifying confounders on gene association scores
The potential confounding effects of six gene properties on the most significant SNP p-value, for all genes g were examined using 1,000 DGI study permutations, described below. The gene features tested include: (1) Physical gene size for gene g, dg, defined as the distance in kilobase (kb) units between the most extreme transcript start and end sites of all isoforms of a given gene (including introns), plus an added distance. For the extended boundaries of −110kb/+40kb used for the mitochondrial and lipid analyses, 150 kb were added, and for the ±50 kb boundaries used for method development purposes, 100 kb were added; (2) Number of genotyped and imputed (if available) SNPs per kb for each gene g, ng; (3) Estimated number of independent SNPs (that are in approximate linkage equilibrium with each other) per kb for each gene g, ug. This was calculated using the –indep option in PLINK that prunes SNPs based on the variance inflation factor, VIF (http://pngu.mgh.harvard.edu/~purcell/plink/summary.shtml#prune; default parameters were used). The genotypes of the CEU population from HapMap version 19 were used, since the GWA samples analyzed in this work are of European descendent. This yielded 310,399 independent autosomal SNPs; (4) Number of recombination hotspots spanning gene g per kb, hg. Recombination hotspot positions were taken from [56]; (5) Genetic distance of each gene g, cg in centi-Morgan (cM) per kb units calculated based on a fine-scale map of recombination rates [56]; and (6) Linkage disequilibrium units (LDU) per kb for each gene g, lg, calculated based on an LDU map downloaded from http://cedar.genetics.soton.ac.uk/pub/PROGRAMS/LDMAP [57]. All variables were calculated based on the extended gene boundaries. All variables but gene size, dg were transformed to ‘per kilobase’ units: variables ng, ug, and hg, were divided by dg, and variables cg and lg were divided by the physical distance between the most extreme genetic markers within the gene boundaries for which genetic distance or LDU data were available. All six variables showed a significant correlation with for all genes g, using 1,000 DGI study permutations, both before and after normalization to gene region size.
Permutation analysis of Diabetes Genetics Initiative GWA study
We used the Diabetes Genetics Initiative (DGI) GWA study [17] as a test case for developing MAGENTA, as we had access to genotypes of all individuals in this study (as opposed to the GWA meta-analyses analyzed in this paper where we do not have access to genotype data). The analysis was done only on the population-based samples of the DGI study - 1,022 cases and 1,075 controls that were matched for age, gender, body mass index and region of origin. Specifically, the T2D case/control labels were randomly permuted 1,000 times between individuals from the same collection center and the same gender. A genome-wide association test (logistic regression) that assumes an additive allelic model (1 degree of freedom) followed by a genomic control (adjustment for lambda larger than 1) was then applied to each of the 381,099 genotyped SNPs across the 1,000 permutations, resulting in an association p-value, for each SNP i and each permutation. was calculated for all genes in the genome, across the 1,000 DGI permutations. A gene p-value adjusted for confounding effects with permutation analysis, was then calculated for each gene g in the genome. is defined as the fraction of permutations whose is equal to or lower (more significant) than the observed DGI . We performed an additional 10,000 case/control permutations for SNPs within ±50 kb around genes with to increase resolution. Genes with were assigned .
The gene score vectors before correction () calculated for the 1,000 DGI permuted data sets were used to quantify the correlation between six gene properties of potential confounding effects on and (Table 1). The permutations were also used to evaluate which of the correlated gene properties had a significant confounding effect on based on a step-wise multivariate linear regression model (Table S3). The resulting significant confounders were used in all gene set analyses presented in this study. To assess the performance of our regression-based correction of confounders on , Sidak's correction and a modified Sidak's correction, we compared the corrected gene p-values, to the corresponding gene p-values corrected with permutation analysis, for all genes g, using the actual DGI study. Permutation analysis was used as the gold standard for adjusting for confounders on SNP to gene scores as it generates gene-specific null distributions while maintaining the physical and genetic structure of SNPs across gene regions. This enables correcting for all possible confounding effects on gene association scores without requiring a priori knowledge of the confounders. The performance of our regression-based correction, Sidak's correction and a modified Sidak's correction were evaluated by comparing the Pearson's correlation coefficient between and to the correlation coefficient between the unadjusted gene score, and for all genes g in the genome.
The permuted for all SNPs i were also used for power simulations described in the next section.
Simulations used to estimate sensitivity and specificity of MAGENTA
We developed a simulation framework to evaluate the power of MAGENTA to identify enrichment of multiple associations for which we have low detection power with single SNP analysis. SNPs with a small effect size were randomly spiked into varying numbers of genes (referred to as causal genes) in pre-specified gene sets (one SNP per gene), and into genes outside the gene set, maintaining the total number of causal genes in the genome. The simulations were performed on a background of randomized SNP association p-values, for all SNPs i in the genome, generated with phenotype permutations of the DGI study (see section above). For each set of parameters tested, 1,000 simulation runs were performed. In each simulation run, the genes representing a simulated gene set of a given size were randomly chosen from the genome, and the various fractions of genes assigned a SNP of small effect size were also randomly chosen from all genes in the gene set. The remaining number of causal SNPs was randomly assigned to genes outside the gene set. The small effects were randomly assigned to SNPs within the ±50kb extended gene boundaries (see above for boundary definition). To eliminate artifacts that could arise from using one specific vector of permuted , each simulation run was done on a different GWA study permutation background that was randomly chosen from 1,000 different DGI phenotype permutations. For each of the 1,000 simulation runs, gene p-values corrected with multivariate regression analysis (see above), were calculated for all genes g in the genome. The GSEA algorithm in MAGENTA was then applied to the simulated gene set with a given fraction of causal genes of weak effect. Finally, GSEA power (i.e. sensitivity) was estimated as the fraction of 1,000 spike-in simulations whose gene set enrichment p-value, exceeded a given significance level (in this study ≤0.01, a suitable cutoff for the few hypotheses tested in the mitochondrial gene set analysis). The power does not decrease significantly when a more stringent cutoff is used: ≤0.001 (Figure S9).
The parameters used in the simulations are: (i) Gene set size of 25, 100 or 1000 genes; (ii) Fraction of genes in a gene set that got assigned a SNP with a modest effect size: 0 (negative control), 1%, 5%, and 10%, 20%, 30%, 40%, 50% and 60%; (iii) The small effect size of each spiked-in SNP was estimated by randomly sampling from a noncentral chi-square distribution with one degree of freedom (assuming an additive allelic test). The non-centrality parameters (NCP) used were: NCP = 0 for estimating specificity or false positive rate of our GSEA method, NCP = 2.5 for a very weak effect size (equivalent to 1% power of detection at p≤1e-4 using single SNP analysis; e.g. odds ratio of 1.03–1.04 for an allele frequency of 0.2–0.3 and sample size of 10,000 individuals [41]; Figure S6A), and NCP = 10 for a modest effect size (equivalent to 1% power of detection at genome-wide significance (p≤5e-8) using single SNP analysis; e.g. odds ratio of 1.07 for an allele frequency of 0.2–0.3 and sample size of 10,000 individuals [41]; Figure 3); and (iv) A total of 100 (Figure 3) or 500 (Figure S6B) causal genes in the genome. The chi-square test statistic was then converted to a z-score by taking the square root of the chi-square test statistic. Parameters were chosen in attempt to reflect what we know about the genetic architecture of complex diseases and traits.
This simulation framework was also used to choose an optimal gene score enrichment cutoff, for our GSEA algorithm. Five cutoffs were tested: 99th, 95th, 90th, 75th, and 50th percentile of all gene p-values for two effect sizes: NCP = 2.5 and NCP = 10, assuming a total of 100 causal genes in the genome. A equivalent to the 95th percentile of for all genes g in the genome yielded the optimal power, when considering power plots for both effect sizes (Figure S5). The 75th percentile cutoff performed a bit better than the 95th percentile cutoff for very weak effects (NCP = 2.5; Figure S5B), especially when assuming a total of 500 causal genes (data not shown). Hence, the 75th percentile cutoff could be used for diseases or traits that are highly polygenic with many associations of weak effects.
Gene sets analyzed with MAGENTA
Mitochondria-related gene sets
Of the 1,012 unique human mitochondrial genes described in MitoCarta [22], we analyzed 966 autosomal mitochondrial genes. This number was obtained after removing 13 genes encoded by the mitochondrial DNA and 31 mitochondrial genes that lie on the X and Y chromosomes, as they were not analyzed in the GWA studies and meta-analyses used in this work. Two autosomal genes were removed, as they were absent from the human gene list used for our analyses. For the DIAGRAM+ T2D meta-analysis, the effective gene set size of all mitochondrial genes was 885 genes, as 11 genes did not have any genotyped or imputed SNPs within their extended gene boundaries (110 kb upstream and 40 kb downstream to the most extreme transcript boundaries) and 70 genes were removed following physical proximity adjustment described in the GSEA section. There are 110,060 unique SNPs that fall within the gene regions of the 966 nuclear-encoded mitochondrial genes, based on the DIAGRAM+ meta-analysis (4.9% of all SNPs).
A list of 91 oxidative phosphorylation (OXPHOS) genes out of the 966 autosomal, mitochondrial genes was manually curated (marked in Table S12). This list does not include 12 OXPHOS genes encoded by the mitochondrial DNA and 3 genes on chromosome X. There are 9,693 SNPs that fall within the gene regions of the 91 OXPHOS genes based on the DIAGRAM+ meta-analysis (0.4% of all SNPs).
A set of 16 known nuclear transcriptional regulators of mitochondrial functions was assembled based on the literature [35], [44]–[48] (Table S11). All mitochondria regulators had SNPs in their extended gene boundaries using the DIAGRAM+ meta-analysis.
Lipid - and lipoprotein-related gene sets
We tested 15 biological processes related to lipid, fatty acid and steroid metabolism defined by the PANTHER classification method (http://www.pantherdb.org/) [42], and 36 gene sets related to lipid, lipoprotein and fatty acid metabolism defined by Gene Ontology [43], which include 7 molecular functions and 29 biological processes. The Gene Ontology gene sets were taken from the Molecular Signatures Database (MsigDB, http://www.broad.mit.edu/gsea/msigdb/collections.jsp).
In this paper we analyzed gene sets with an initial gene set size of 10 genes or more.
Software
MAGENTA is freely available for use at http://broadinstitute.org/mpg/magenta.
Supporting Information
Zdroje
1. LowellBB
ShulmanGI
2005 Mitochondrial dysfunction and type 2 diabetes. Science 307 384 387 doi:10.1126/science.1104343
2. DumasJ
SimardG
FlammentM
DucluzeauP
RitzP
2009 Is skeletal muscle mitochondrial dysfunction a cause or an indirect consequence of insulin resistance in humans? Diabetes Metab 35 159 167 doi:10.1016/j.diabet.2009.02.002
3. TaylorRW
TurnbullDM
2005 Mitochondrial DNA mutations in human disease. Nat Rev Genet 6 389 402 doi:10.1038/nrg1606
4. JinW
PattiM
2009 Genetic determinants and molecular pathways in the pathogenesis of Type 2 diabetes. Clin Sci 116 99 111 doi:10.1042/CS20080090
5. KelleyDE
HeJ
MenshikovaEV
RitovVB
2002 Dysfunction of mitochondria in human skeletal muscle in type 2 diabetes. Diabetes 51 2944 2950
6. ChoYM
ParkKS
LeeHK
2007 Genetic factors related to mitochondrial function and risk of diabetes mellitus. Diabetes Res Clin Pract 77 Suppl 1 S172 177 doi:10.1016/j.diabres.2007.01.052
7. TurnerN
HeilbronnLK
2008 Is mitochondrial dysfunction a cause of insulin resistance? Trends Endocrinol Metab 19 324 330 doi:10.1016/j.tem.2008.08.001
8. PetersenKF
DufourS
BefroyD
GarciaR
ShulmanGI
2004 Impaired mitochondrial activity in the insulin-resistant offspring of patients with type 2 diabetes. N Engl J Med 350 664 671 doi:10.1056/NEJMoa031314
9. MoothaVK
LindgrenCM
ErikssonK
SubramanianA
SihagS
2003 PGC-1alpha-responsive genes involved in oxidative phosphorylation are coordinately downregulated in human diabetes. Nat Genet 34 267 273 doi:10.1038/ng1180
10. PattiME
ButteAJ
CrunkhornS
CusiK
BerriaR
2003 Coordinated reduction of genes of oxidative metabolism in humans with insulin resistance and diabetes: Potential role of PGC1 and NRF1. Proc Natl Acad Sci USA 100 8466 8471 doi:10.1073/pnas.1032913100
11. KovesTR
UssherJR
NolRC
SlentzD
MosedaleM
n.d. Mitochondrial Overload and Incomplete Fatty Acid Oxidation Contribute to Skeletal Muscle Insulin Resistance. Cell Metabolism Available: http://www.sciencedirect.com.ezp-prod1.hul.harvard.edu/science?_ob=ArticleURL&_udi=B7MFH-4RJ518M-8&_user=209690&_coverDate=01%2F31%2F2008&_alid=1179716171&_rdoc=1&_fmt=high&_orig=search&_cdi=23259&_st=1&_docanchor=&_ct=14&_acct=C000014438&_version=1&_urlVersion=0&_userid=209690&md5=d8d4b7c3bc5ff26bd8514308c4d89cd5. Accessed 25 Jan 2010
12. SchiffM
LoublierS
CoulibalyA
BénitP
Ogier de BaulnyH
2009 Mitochondria and diabetes mellitus: untangling a conflictive relationship? J Inherit Metab Dis Available: http://www.ncbi.nlm.nih.gov.ezp-prod1.hul.harvard.edu/pubmed/19821144. Accessed 7 Dec 2009
13. ReilingE
van Vliet-OstaptchoukJV
van 't RietE
van HaeftenTW
ArpPA
2009 Genetic association analysis of 13 nuclear-encoded mitochondrial candidate genes with type II diabetes mellitus: the DAMAGE study. Eur J Hum Genet 17 1056 1062 doi:10.1038/ejhg.2009.4
14. JiaJ
TianY
CaoZ
TaoL
ZhangX
n.d. The polymorphisms of UCP1 genes associated with fat metabolism, obesity and diabetes. Molecular Biology Reports Available: http://dx.doi.org.ezp-prod1.hul.harvard.edu/10.1007/s11033-009-9550-2. Accessed 7 Dec 2009
15. AndrulionytèL
ZacharovaJ
ChiassonJ
LaaksoM
2004 Common polymorphisms of the PPAR-gamma2 (Pro12Ala) and PGC-1alpha (Gly482Ser) genes are associated with the conversion from impaired glucose tolerance to type 2 diabetes in the STOP-NIDDM trial. Diabetologia 47 2176 2184 doi:10.1007/s00125-004-1577-2
16. SaxenaR
de BakkerPIW
SingerK
MoothaV
BurttN
2006 Comprehensive association testing of common mitochondrial DNA variation in metabolic disease. Am J Hum Genet 79 54 61 doi:10.1086/504926
17. SaxenaR
VoightBF
LyssenkoV
BurttNP
de BakkerPIW
2007 Genome-wide association analysis identifies loci for type 2 diabetes and triglyceride levels. Science 316 1331 1336 doi:10.1126/science.1142358
18. ScottLJ
MohlkeKL
BonnycastleLL
WillerCJ
LiY
2007 A genome-wide association study of type 2 diabetes in Finns detects multiple susceptibility variants. Science 316 1341 1345 doi:10.1126/science.1142382
19. ZegginiE
WeedonMN
LindgrenCM
FraylingTM
ElliottKS
2007 Replication of genome-wide association signals in UK samples reveals risk loci for type 2 diabetes. Science 316 1336 1341 doi:10.1126/science.1142364
20. ZegginiE
ScottLJ
SaxenaR
VoightBF
MarchiniJL
2008 Meta-analysis of genome-wide association data and large-scale replication identifies additional susceptibility loci for type 2 diabetes. Nat Genet 40 638 645 doi:10.1038/ng.120
21. FarrisW
LeissringMA
HemmingML
ChangAY
SelkoeDJ
2005 Alternative splicing of human insulin-degrading enzyme yields a novel isoform with a decreased ability to degrade insulin and amyloid beta-protein. Biochemistry 44 6513 6525 doi:10.1021/bi0476578
22. PagliariniDJ
CalvoSE
ChangB
ShethSA
VafaiSB
2008 A mitochondrial protein compendium elucidates complex I disease biology. Cell 134 112 123 doi:10.1016/j.cell.2008.06.016
23. WangK
LiM
BucanM
2007 Pathway-Based Approaches for Analysis of Genomewide Association Studies. Am J Hum Genet 81 Available: http://www.ncbi.nlm.nih.gov.ezp-prod1.hul.harvard.edu/pubmed/17966091. Accessed 5 Nov 2009
24. SubramanianA
TamayoP
MoothaVK
MukherjeeS
EbertBL
2005 Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc Natl Acad Sci USA 102 15545 15550 doi:10.1073/pnas.0506580102
25. HongM
PawitanY
MagnussonPKE
PrinceJA
2009 Strategies and issues in the detection of pathway enrichment in genome-wide association studies. Hum Genet 126 289 301 doi:10.1007/s00439-009-0676-z
26. PengG
LuoL
SiuH
ZhuY
HuP
2010 Gene and pathway-based second-wave analysis of genome-wide association studies. Eur J Hum Genet 18 111 117 doi:10.1038/ejhg.2009.115
27. PerryJRB
McCarthyMI
HattersleyAT
ZegginiE
WeedonMN
2009 Interrogating type 2 diabetes genome-wide association data using a biological pathway-based approach. Diabetes 58 1463 1467 doi:10.2337/db08-1378
28. ElbersCC
van EijkKR
FrankeL
MulderF
van der SchouwYT
2009 Using genome-wide pathway analysis to unravel the etiology of complex diseases. Genet Epidemiol 33 419 431 doi:10.1002/gepi.20395
29. EleftherohorinouH
WrightV
HoggartC
HartikainenA
JarvelinM
2009 Pathway Analysis of GWAS Provides New Insights into Genetic Susceptibility to 3 Inflammatory Diseases. PLoS ONE 4 e8068 doi:10.1371/journal.pone.0008068
30. WangK
ZhangH
KugathasanS
AnneseV
BradfieldJP
2009 Diverse genome-wide association studies associate the IL12/IL23 pathway with Crohn Disease. Am J Hum Genet 84 399 405 doi:10.1016/j.ajhg.2009.01.026
31. BaranziniSE
GalweyNW
WangJ
KhankhanianP
LindbergR
2009 Pathway and network-based analysis of genome-wide association studies in multiple sclerosis. Hum Mol Genet 18 2078 2090 doi:10.1093/hmg/ddp120
32. ChasmanDI
2008 On the utility of gene set methods in genomewide association studies of quantitative traits. Genet Epidemiol 32 658 668 doi:10.1002/gepi.20334
33. ChaiH
SicotteH
BaileyKR
TurnerST
AsmannYW
2009 GLOSSI: a method to assess the association of genetic loci-sets with complex diseases. BMC Bioinformatics 10 102 doi:10.1186/1471-2105-10-102
34. KathiresanS
WillerCJ
PelosoGM
DemissieS
MusunuruK
2009 Common variants at 30 loci contribute to polygenic dyslipidemia. Nat Genet 41 56 65 doi:10.1038/ng.291
35. KellyDP
ScarpullaRC
2004 Transcriptional regulatory circuits controlling mitochondrial biogenesis and function. Genes Dev 18 357 368 doi:10.1101/gad.1177604
36. VoightBF
ScottLJ
SteinthorsdottirV
MorrisAP
DinaC
2010 Twelve type 2 diabetes susceptibility loci identified through large-scale association analysis. Nature Genetics (in press)
37. DupuisJ
LangenbergC
ProkopenkoI
SaxenaR
SoranzoN
2010 New genetic loci implicated in fasting glucose homeostasis and their impact on type 2 diabetes risk. Nat Genet 42 105 116 doi:10.1038/ng.520
38. SaxenaR
HivertM
LangenbergC
TanakaT
PankowJS
2010 Genetic variation in GIPR influences the glucose and insulin responses to an oral glucose challenge. Nat Genet 42 142 148 doi:10.1038/ng.521
39. NealeBM
ShamPC
2004 The future of association studies: gene-based analysis and replication. Am J Hum Genet 75 353 362 doi:10.1086/423901
40. SacconeSF
HinrichsAL
SacconeNL
ChaseGA
KonvickaK
2007 Cholinergic nicotinic receptor genes implicated in a nicotine dependence association study targeting 348 candidate genes with 3713 SNPs. Hum Mol Genet 16 36 49 doi:10.1093/hmg/ddl438
41. PurcellS
ChernySS
ShamPC
2003 Genetic Power Calculator: design of linkage and association genetic mapping studies of complex traits. Bioinformatics 19 149 150
42. ThomasPD
CampbellMJ
KejariwalA
MiH
KarlakB
2003 PANTHER: A Library of Protein Families and Subfamilies Indexed by Function. Genome Research 13 2129 2141 doi:10.1101/gr.772403
43. AshburnerM
BallCA
BlakeJA
BotsteinD
ButlerH
2000 Gene ontology: tool for the unification of biology. The Gene Ontology Consortium. Nat Genet 25 25 29 doi:10.1038/75556
44. WanJ
JiangL
LüQ
KeL
LiX
2009 Activation of PPARdelta up-regulates fatty acid oxidation and energy uncoupling genes of mitochondria and reduces palmitate-induced apoptosis in pancreatic beta-cells. Biochem Biophys Res Commun Available: http://www.ncbi.nlm.nih.gov.ezp-prod1.hul.harvard.edu/pubmed/20040361. Accessed 13 Jan 2010
45. GoffartS
WiesnerRJ
2003 Regulation and co-ordination of nuclear gene expression during mitochondrial biogenesis. Exp Physiol 88 33 40
46. FinckBN
KellyDP
2006 PGC-1 coactivators: inducible regulators of energy metabolism in health and disease. J Clin Invest 116 615 622 doi:10.1172/JCI27794
47. GiguèreV
2008 Transcriptional control of energy homeostasis by the estrogen-related receptors. Endocr Rev 29 677 696 doi:10.1210/er.2008-0017
48. YuJ
AuwerxJ
2009 The role of sirtuins in the control of metabolic homeostasis. Ann N Y Acad Sci 1173 Suppl 1 E10 19 doi:10.1111/j.1749-6632.2009.04952.x
49. MatthewsDR
HoskerJP
RudenskiAS
NaylorBA
TreacherDF
1985 Homeostasis model assessment: insulin resistance and beta-cell function from fasting plasma glucose and insulin concentrations in man. Diabetologia 28 412 419
50. MoothaVK
HandschinC
ArlowD
XieX
St PierreJ
2004 Erralpha and Gabpa/b specify PGC-1alpha-dependent oxidative phosphorylation gene expression that is altered in diabetic muscle. Proc Natl Acad Sci USA 101 6570 6575 doi:10.1073/pnas.0401401101
51. FinleyLWS
HaigisMC
2009 The coordination of nuclear and mitochondrial communication during aging and calorie restriction. Ageing Res Rev 8 173 188 doi:10.1016/j.arr.2009.03.003
52. LiangF
KumeS
KoyaD
2009 SIRT1 and insulin resistance. Nat Rev Endocrinol 5 367 373 doi:10.1038/nrendo.2009.101
53. PurcellSM
WrayNR
StoneJL
VisscherPM
O'DonovanMC
2009 Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature 460 748 752 doi:10.1038/nature08185
54. VeyrierasJ
KudaravalliS
KimSY
DermitzakisET
GiladY
2008 High-resolution mapping of expression-QTLs yields insight into human gene regulation. PLoS Genet 4 e1000214 doi:10.1371/journal.pgen.1000214
55. SokalRR
RohlfFJ
1995 Biometry: The principles and Practice of Statistics in Biological Research. Third Edition. W.H. Freeman and Company, New York
56. MyersS
BottoloL
FreemanC
McVeanG
DonnellyP
2005 A fine-scale map of recombination rates and hotspots across the human genome. Science 310 321 324 doi:10.1126/science.1117196
57. TapperW
CollinsA
GibsonJ
ManiatisN
EnnisS
2005 A map of the human genome in linkage disequilibrium units. Proc Natl Acad Sci USA 102 11835 11839 doi:10.1073/pnas.0505262102
Štítky
Genetika Reprodukční medicína
Článek vyšel v časopisePLOS Genetics
Nejčtenější tento týden
2010 Číslo 8- Akutní intermitentní porfyrie
- Souvislost haplotypu M2 genu pro annexin A5 s opakovanými reprodukčními ztrátami
- Primární hyperoxalurie – aktuální možnosti diagnostiky a léčby
- Doc. Miloš Kubánek: Nemocní se srdeční amyloidózou jsou často skryti a sledováni pod jinými diagnózami
- Transthyretinová amyloidóza z pohledu neurologa a kardiologa aneb jak se vyhnout „misdiagnostice“?
-
Všechny články tohoto čísla
- A Model for Damage Load and Its Implications for the Evolution of Bacterial Aging
- Mutation in the Gene Encoding Ubiquitin Ligase LRSAM1 in Patients with Charcot-Marie-Tooth Disease
- Identification of the Bovine Arachnomelia Mutation by Massively Parallel Sequencing Implicates Sulfite Oxidase (SUOX) in Bone Development
- Did Genetic Drift Drive Increases in Genome Complexity?
- The 5p15.33 Locus Is Associated with Risk of Lung Adenocarcinoma in Never-Smoking Females in Asia
- An Alpha-Catulin Homologue Controls Neuromuscular Function through Localization of the Dystrophin Complex and BK Channels in
- Epigenetically-Inherited Centromere and Neocentromere DNA Replicates Earliest in S-Phase
- Survival and Growth of Yeast without Telomere Capping by Cdc13 in the Absence of Sgs1, Exo1, and Rad9
- Tuberous Sclerosis Complex 1 Regulates dE2F1 Expression during Development and Cooperates with RBF1 to Control Proliferation and Survival
- Disease-Associated Mutations That Alter the RNA Structural Ensemble
- The Transcriptomes of Two Heritable Cell Types Illuminate the Circuit Governing Their Differentiation
- Inactivation of VCP/ter94 Suppresses Retinal Pathology Caused by Misfolded Rhodopsin in
- Multiple Independent Loci at Chromosome 15q25.1 Affect Smoking Quantity: a Meta-Analysis and Comparison with Lung Cancer and COPD
- Transcriptional Regulation by CHIP/LDB Complexes
- Conserved Role of in Ethanol Responses in Mutant Mice
- A Global Overview of the Genetic and Functional Diversity in the Pathogenicity Island
- Common Inherited Variation in Mitochondrial Genes Is Not Enriched for Associations with Type 2 Diabetes or Related Glycemic Traits
- Extracellular Dopamine Potentiates Mn-Induced Oxidative Stress, Lifespan Reduction, and Dopaminergic Neurodegeneration in a BLI-3–Dependent Manner in
- Genetic Analysis of Baker's Yeast Msh4-Msh5 Reveals a Threshold Crossover Level for Meiotic Viability
- Genome-Wide Association Studies of Serum Magnesium, Potassium, and Sodium Concentrations Identify Six Loci Influencing Serum Magnesium Levels
- Something New: An Interview with Radoje Drmanac
- The Extinction Dynamics of Bacterial Pseudogenes
- Microtubule Actin Crosslinking Factor 1 Regulates the Balbiani Body and Animal-Vegetal Polarity of the Zebrafish Oocyte
- Consistent Association of Type 2 Diabetes Risk Variants Found in Europeans in Diverse Racial and Ethnic Groups
- Transmission of Mitochondrial DNA Diseases and Ways to Prevent Them
- Telomere Disruption Results in Non-Random Formation of Dicentric Chromosomes Involving Acrocentric Human Chromosomes
- Chromosome Axis Defects Induce a Checkpoint-Mediated Delay and Interchromosomal Effect on Crossing Over during Drosophila Meiosis
- Dynamic Chromatin Organization during Foregut Development Mediated by the Organ Selector Gene PHA-4/FoxA
- Ancient Protostome Origin of Chemosensory Ionotropic Glutamate Receptors and the Evolution of Insect Taste and Olfaction
- A Wnt-Frz/Ror-Dsh Pathway Regulates Neurite Outgrowth in
- PLOS Genetics
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Identification of the Bovine Arachnomelia Mutation by Massively Parallel Sequencing Implicates Sulfite Oxidase (SUOX) in Bone Development
- Common Inherited Variation in Mitochondrial Genes Is Not Enriched for Associations with Type 2 Diabetes or Related Glycemic Traits
- A Model for Damage Load and Its Implications for the Evolution of Bacterial Aging
- Did Genetic Drift Drive Increases in Genome Complexity?
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání



