A Model for Damage Load and Its Implications for the Evolution of Bacterial Aging
Deleterious mutations appearing in a population increase in frequency until stopped by natural selection. The ensuing equilibrium creates a stable frequency of deleterious mutations or the mutational load. Here I develop the comparable concept of a damage load, which is caused by harmful non-heritable changes to the phenotype. A damage load also ensues when the increase of damage is opposed by selection. The presence of a damage load favors the evolution of asymmetrical transmission of damage by a mother to her daughters. The asymmetry is beneficial because it increases fitness variance, but it also leads to aging or senescence. A mathematical model based on microbes reveals that a cell lineage dividing symmetrically is immortal if lifetime damage rates do not exceed a threshold. The evolution of asymmetry allows the lineage to persist above the threshold, but the lineage becomes mortal. In microbes with low genomic mutation rates, it is likely that the damage load is much greater than the mutational load. In metazoans with higher genomic mutation rates, the damage and the mutational load could be of the same magnitude. A fit of the model to experimental data shows that Escherichia coli cells experience a damage rate that is below the threshold and are immortal under the conditions examined. The model estimates the asymmetry level of E. coli to be low but sufficient for persisting at higher damage rates. The model also predicts that increasing asymmetry results in diminishing fitness returns, which may explain why the bacterium has not evolved higher asymmetry.
Published in the journal:
. PLoS Genet 6(8): e32767. doi:10.1371/journal.pgen.1001076
Category:
Research Article
doi:
https://doi.org/10.1371/journal.pgen.1001076
Summary
Deleterious mutations appearing in a population increase in frequency until stopped by natural selection. The ensuing equilibrium creates a stable frequency of deleterious mutations or the mutational load. Here I develop the comparable concept of a damage load, which is caused by harmful non-heritable changes to the phenotype. A damage load also ensues when the increase of damage is opposed by selection. The presence of a damage load favors the evolution of asymmetrical transmission of damage by a mother to her daughters. The asymmetry is beneficial because it increases fitness variance, but it also leads to aging or senescence. A mathematical model based on microbes reveals that a cell lineage dividing symmetrically is immortal if lifetime damage rates do not exceed a threshold. The evolution of asymmetry allows the lineage to persist above the threshold, but the lineage becomes mortal. In microbes with low genomic mutation rates, it is likely that the damage load is much greater than the mutational load. In metazoans with higher genomic mutation rates, the damage and the mutational load could be of the same magnitude. A fit of the model to experimental data shows that Escherichia coli cells experience a damage rate that is below the threshold and are immortal under the conditions examined. The model estimates the asymmetry level of E. coli to be low but sufficient for persisting at higher damage rates. The model also predicts that increasing asymmetry results in diminishing fitness returns, which may explain why the bacterium has not evolved higher asymmetry.
Introduction
Evolution by natural selection generally produces phenotypes that maximize fitness, but many factors can interfere. Genetic constraints can lead to a suboptimal phenotype, but an optimal phenotype may not be achieved even when an optimal genotype is possible. If the rate of deleterious mutations is sufficiently high, selection is unable to eliminate all mutations and a mutation-selection equilibrium at a lower fitness ensues. An asexual population has at equilibrium a mean fitness of(1)where U is the deleterious genomic mutation rate [1], [2]. The mutational load equals (references [3]–[5]).
However, an optimal phenotype can also be prevented by the direct action of non-heritable damage. Bones can be broken, muscles torn, and macromolecules oxidized. All these lower fitness despite the perfection of the genotype. Although the study of deleterious mutations is long standing in evolution [1]–[7], interest in damage is recent. The transmission of deleterious mutations across generations follows the rules of genetics. While damage is not heritable, it can still be transmitted from mother to daughter and its transmission rules are just being explored as an evolutionary phenomenon [8]–[11]. Here I develop the concept of a damage load and analyze its evolutionary consequences. Mutational and damage loads may appear on the surface similar, but key and fundamental differences are revealed by a comparison. Because recent experimental work has stimulated an interest in the effects of damage in microbes [12]–[14], the analysis focuses on a single-celled organism reproducing by binary fission.
A model for damage load can be developed by allowing the generation of damage, the operation of selection, and the attainment of the ensuing damage-selection equilibrium. Recent models have in fact used such an approach to examine the evolution of transmission rules for damage, i.e. how a mother cell distributes her damage to her two daughter cells [8]–[11]. However, with the exception of the most recent model by Erjavec et al. [11] all of these models were limited because a key difference between damage and mutations is the timing of their effects. In metazoans, the consequences of damage are immediate because the soma is affected. Mutational damage to the germline is delayed to the next generation. Because somatic mutations are not inherited through the germline, they are effectively non-heritable in most organisms and equivalent to damage for the present analysis. For single-celled organisms damage such as oxidized proteins has immediate effects, while genetic damage is again delayed in expression. If damage acts immediately, an early event during the lifetime of an organism has more impact than a later one. More importantly, an early damage can extend generation time and expose the organism to even more damage.
To incorporate the timing of damage, a new model was developed. The model shared some similarities with the one by Erjavec et al., but it assumed instead that the effect of damage was linear. Ackermann et al. [8] examined a range of damage effects, including a linear relationship, but their effects were mapped directly to fitness and thus did not incorporate the timing of damage. Given that evidence supporting either a linear or higher order effect of damage is lacking, a linear assumption is parsimoniously reasonable and provides more statistical power by reducing the number of parameters. Linearity additionally allows for simpler but explicit solutions and facilitates fitting data to estimate key parameters in the model.
Model
Let k0 be the amount of damage a mother cell receives at birth. She immediately acquires new damage and, if λ is the intrinsic rate of damage, her damage at any time t is
To divide into two daughter cells, the mother cell is assumed to build up an intracellular product P to a checkpoint Π. Assuming that damage hinders function linearly, P accumulates at a rate(2a)(2b)by integration and letting t = T0 and P(T0) = Π when the mother cell divides and T0 is her doubling time. The integration constant P(0) is set to zero because a new pool of the product P is assumed to be built de novo for every cell division. If k0 = λ = 0, T0 = Π in Equation 2b. Thus, Π represents both the checkpoint and the shortest possible doubling time achieved by the fittest and damage-free bacteria. The dual meaning of Π results because dP/dt is scaled to have a maximum value of 1 in the absence of damage (k0 = λ = 0 in Equation 2a). The scaling assumes that P increases linearly with time in the absence of damage and also renders time into units of P. Although the true regulator of bacterial division is not known [15], [16], a model requiring the build-up of a product to a checkpoint is reasonable [11]. Various cellular (volume, mass and length) and biochemical attributes have been postulated to serve as checkpoints, but distinguishing between primary (causative) and secondary (downstream) regulators has been difficult. Regardless, the constancy of bacterial cell size shows that some accounting mechanism and a checkpoint must exist.
Upon dividing, the mother cell partitions her damage D0 to two daughters andTo allow for variation in the partitioning, let a and (1−a) be the proportion of D0 given to the daughters, which are subscripted 1 and 2 and 0≤a≤½. Thus, daughter 1 always receives less damage if a<½ and the damage given to the daughters is(3a)(3b)Because each daughter in turn becomes a mother, Equation 2b can be subscripted to describe the daughters or(4)(5)by the quadratic formula and i = 1 or 2.
Thus, given T0 for a mother cell, Ti of her two daughters can be determined. k0 in Equations 3a and 3b is obtained by rearranging Equation 2b as(6)The ability to predict T1 and T2 given T0 allows projecting forward in time the doubling time, and hence fitness, of every individual in a population. T1 and T2 serve as T0 for the next generation and Equations 3, 5 and 6 only need to be reiterated. Equations 3, 5 and 6 are hereafter referred to as the model.
Results
Equilibrium Conditions
To determine if a lineage of dividing cells converged to a determinable level of damage over successive generations, the model was examined for equilibria. Daughter cells reach an equilibrium when and . Substituting these conditions into Equations 3a and 3b, yields(7a)(7b)where α = a/(1−a). Substituting Equations 7a and 7b into Equation 4(8a)(8b)Equilibrium values and are possible if roots to the quadratic solutions of Equations 8a and 8b are real or(9a)(9b)Thus, equilibria are possible, depending on the level of asymmetry and the product of the two parameters Π and λ. The linking of Π and λ into a single product or fundamental parameter facilitates the analysis of the model by reducing the effective number of parameters in the model from three to two. Because λ is the intrinsic damage rate and Π is the doubling or life time of a damage-free individual (Equation 2b), all damage in such a cell is acquired over its lifetime and Πλ represents its total or lifetime damage rate.
Equilibrium with Symmetrical Transmission
The partitioning of damage from the mother cell to her daughter cells is symmetrical if a = ½, in which case the daughters are identical, k1 = k2, and T1 = T2. Letting i = 1 represent both daughters, the equilibrium conditions are provided by Equation 8a with α = 1 or(10)The roots to Equation 10 are real if(11)
The equilibrium can be locally stable and the stability can be assessed graphically (Figure 1A). The stability results because the doubling times in a lineage descending from a mother cell with a doubling time less than increase until equaling . On the other hand, if the doubling time of a mother cell is greater than , the doubling time of her lineage decreases to .
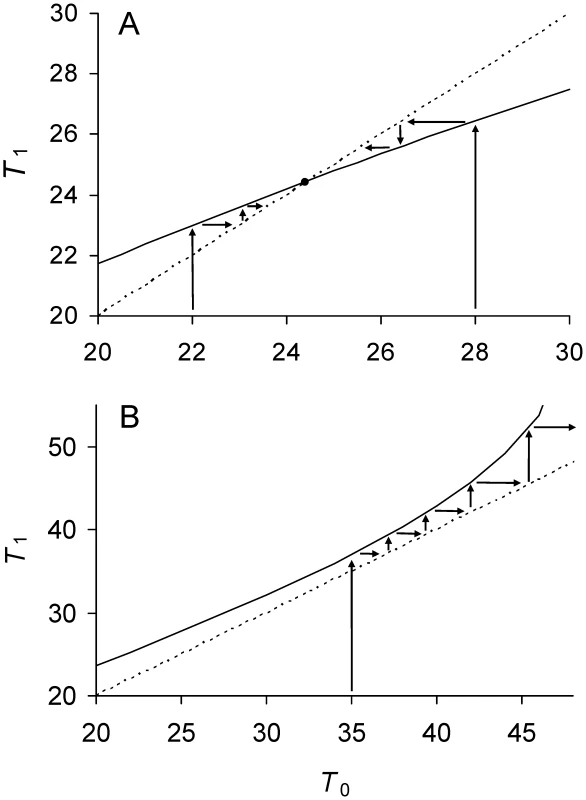
If Πλ>1/6, the doubling time of a lineage never attains an equilibrium and it increases over generations until it is infinitely long (Figure 1B). When doubling time is infinitely long, a mother cell is alive but unable to divide because its damage content is too high and P cannot be built up to Π. At the threshold of Πλ = 1/6, P is built up to Π and, by Equation 10, , which corresponds to the equilibrium doubling time of the least fit symmetrical cell.
To obtain an estimate of the damage load as with symmetrical transmission, the equilibrium mean fitness was estimated for a population of cells with doubling time of relative to a population with the highest fitness or the shortest possible doubling time of Π (Equation 2b). A population with doubling time of Π increases by definition by a factor of 2 during a time period Π. A population with a doubling time of increases during the same period by a factor of . The mean relative fitness at equilibrium resulting from damage is therefore the ratio of , or(12)(13)by letting equal Equation 10.
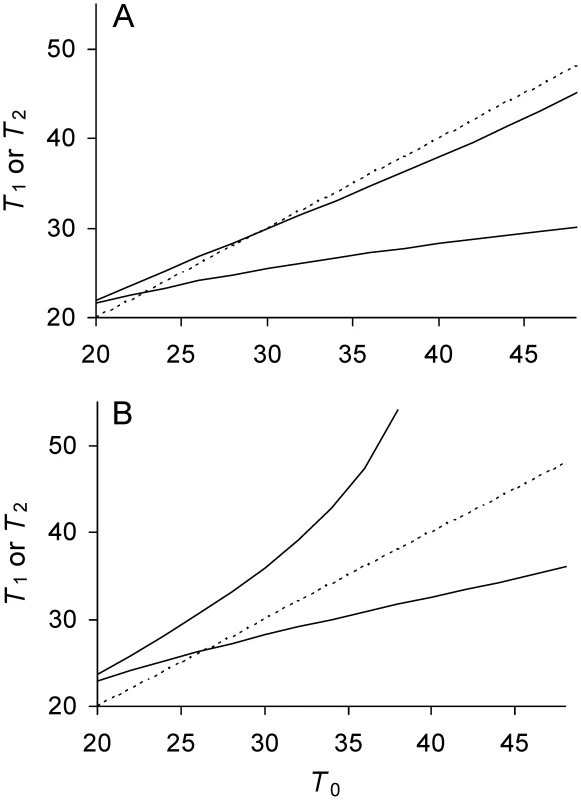
A summary of the results, including new ones to follow, and the definitions of all parameters and variables for the model are presented in Table 1.
Transmission Rules with Asymmetry
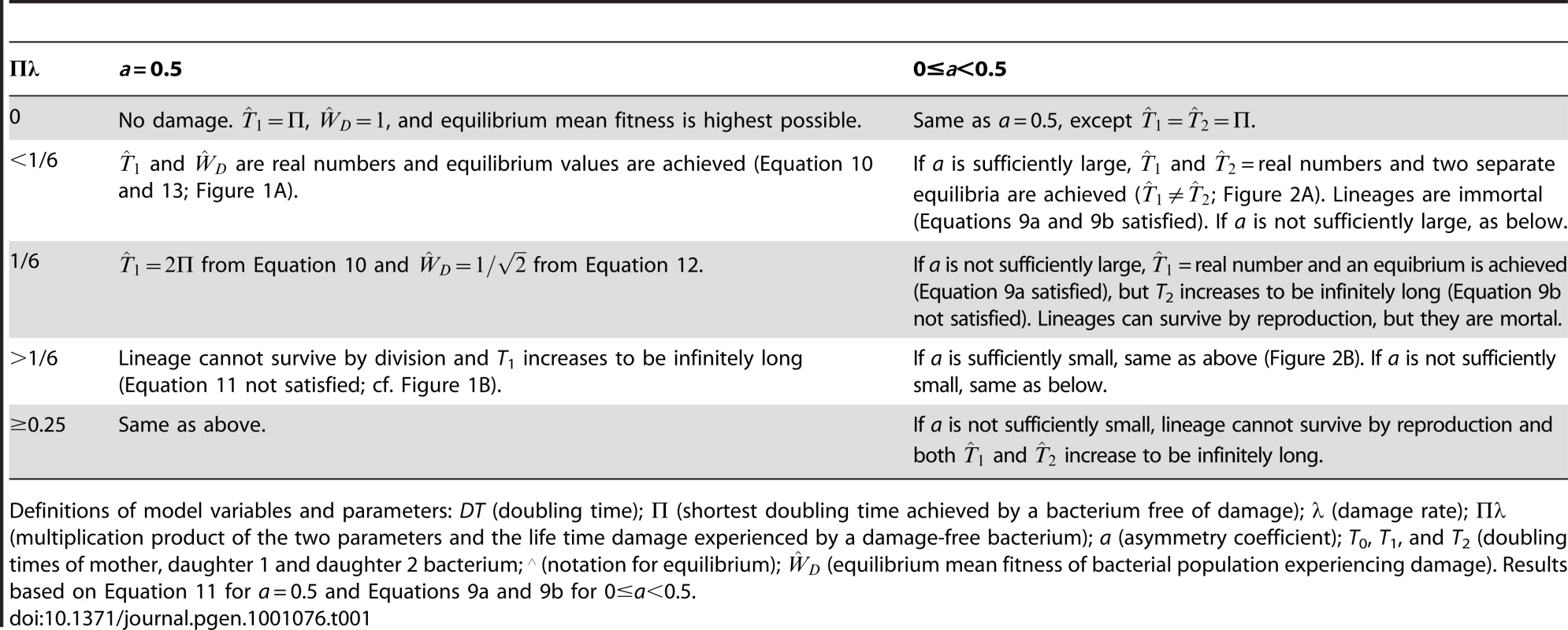
The evolution of the asymmetrical transmission of damage can be examined by letting 0≤a<½. Unlike a = ½ (Figure 1A), a separate equilibrium is now possible for each of the daughters (Equations 8a, 8b). Because a<½, daughter 1 gets less damage. Inspection of Equations 9a and 9b reveals that as Πλ increases from zero, and go through conditions in which both, one or none attain real equilibrium values (Table 1). If Πλ<1/6 and a is sufficiently large, Equations 9a and 9b are satisfied and both and attain equilibria (Figure 2A). If a is not sufficiently large, only Equation 9a is satisfied and has an equilibrium while does not. The same outcome ensues if Πλ≥1/6 and a is sufficiently small (Figure 2B). Thus, the threshold of Πλ = 1/6 still plays an important role (Table 1).
If 0≤a<½, unlike when a = ½, knowing the values and does not allow an estimate of . and represent extreme values to which the doubling time of daughters converge as they replicate, e.g., as it would be illustrated if a graphical projection (see Figure 1) were applied to Figure 2. As new daughter 1 and 2 cells are generated, lineages descending from each type converge to and , respectively, if the equilibria exist. If a daughter 1 is at the equilibrium , it still generates daughter 2 cells, which create new lineages that now converge onto . The presence of different lineages generates a population with mixed doubling times. The distribution of doubling times in the population is in turn shaped by natural selection and can be estimated only after the distribution reaches a selection-damage equilibrium. In contrast, if a = ½, offers a direct estimate of (Equation 10) because a population with mixed doubling times is not possible at equilibrium. Once a lineage converges to all descending daughters have a doubling time of .
was therefore estimated by using the model to simulate a population of cells under selection until a fitness equilibrium was reached. Selection was imposed by allowing cells with shortest doubling times to divide before other cells (Figure 3; Table 1). Πλ behaves again as a single parameter because the model uses Equation 5, which when combined with Equation 12 collapses Π and λ into a product. For values of 0<Πλ<1/6, is highest with a = 0 and maximum asymmetry is favored. However, the advantage shrinks as Πλ decreases to zero. The difference between for a = ½ and a = 0 decreased from 8.6%, 0.57% to 0.0025% when Πλ goes from 0.165, 0.1 to 0.01. For Πλ>1/6, asymmetry is favored more strongly but relationship between and Πλ is non-monotonic. When Πλ = 0.17, is maximized at a = 0.1 and an intermediate asymmetry is favored. Such non-monotonicity is also present, but less apparent, for other values of Πλ, including when Πλ<1/6.
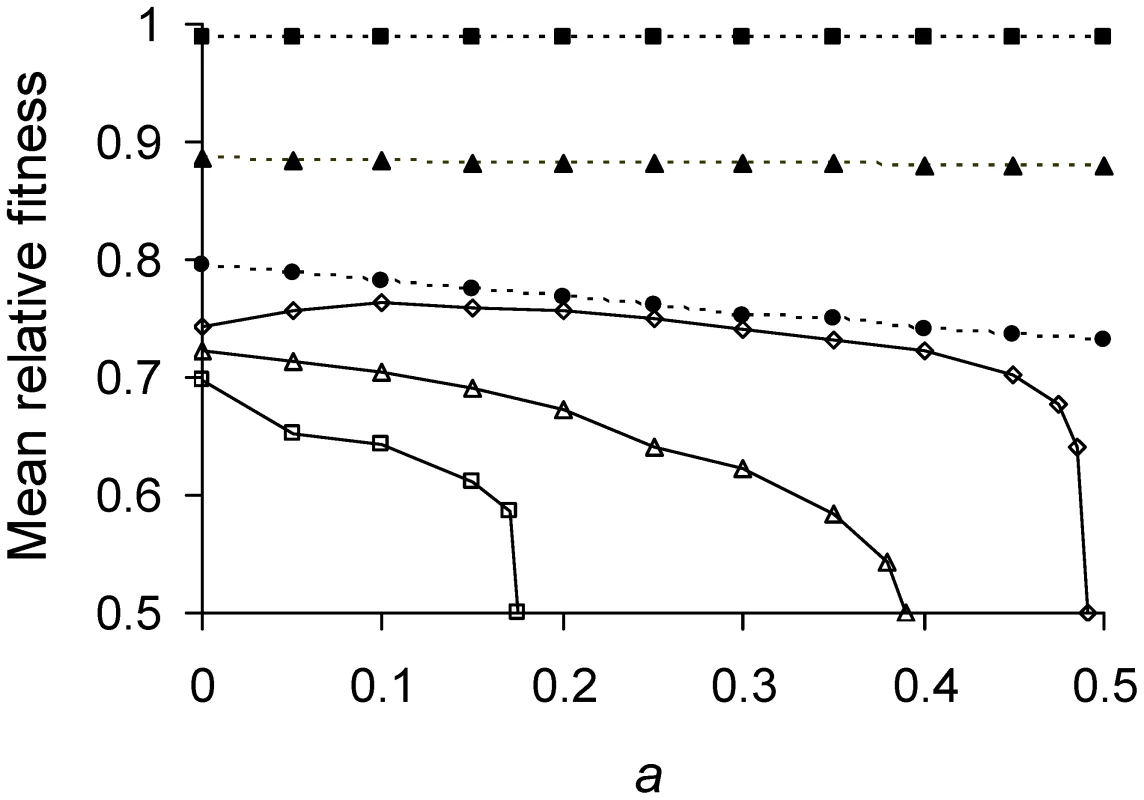
Inspection of the relationship between and a for extreme values reveals why it is not monotonic for Πλ>1/6. Simulations showed that for Πλ>0.25 populations were unable to grow, regardless of a. When Πλ>0.25 and a = 0, Equation 9a is satisfied and daughter 1 achieves its equilibrium of . However, daughter 2 from a cell at receives too much damage and is unable to divide. Thus, the mother cell just replaces herself with daughter 1 and there is no net reproduction. A similar effect explains the left side of the hump when Πλ = 0.17 (Figure 3). However, in this case declines not because daughter 2 is unable to divide, but because the grand-daughter 2 is unable (analysis not presented). The right side of the hump for Πλ = 0.17 results because with low asymmetry Equation 9a is not satisfied and daughter 1 is now unable to divide. The combination of all these effects explains also many of the inflections seen in Figure 3.
Estimating Model Parameters
Recent E. coli data [14] reporting growth rates of mother and daughter cells allow determining where in the parameter space of the model a biological organism resides. By converting the reported growth rates to doubling times, observed values of T0, T1 and T2 were obtained for the bacterium (Figure 4). Each observed T0 was then inputted into the model over the parameter space to derive expected T1 and T2 values. The parameters of the model were determined as those that minimized the difference between the observed and expected T1 and T2 by maximum likelihood via a conjugate gradient method implemented in the software package HyPhy [17]. The parameter a was estimated to have a mean value of 0.4836 and a 95% Bayesian Confidence Interval (BCI) of [0.4716–0.4905]. Estimated mean value of Π was 18.95 min (95% BCI [16.61–21.71]) and of λ was 0.007737 min−1 (95% BCI [0.005347–0.009717]). Applying these mean values of Π, λ, and a to Equations 8a and 8b estimated of and min, which show that the doubling times of the two daughter lineages attained separate equilibria. The presence of these two equilibria in E. coli was also revealed by a phase plot overlaying the observed and expected values (Figure 4).
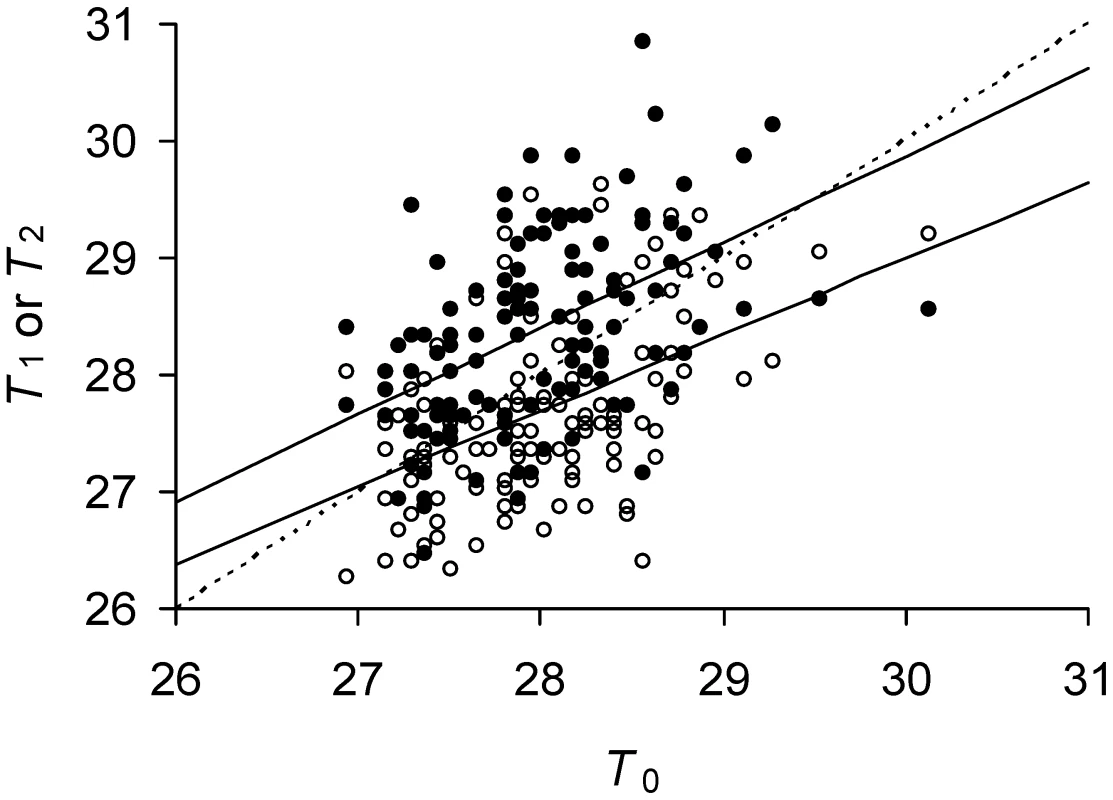
Applying the estimates of Πλ = (18.95)(0.007737) = 0.1467 and a = 0.4836 to the model also showed that was higher, though only by a small amount, for these E. coli relative to a symmetrical (a = ½) bacterium with the same value of Πλ (Figure 5A). However, the advantage became greater if Πλ were increased. While bacteria with a = ½ could not reproduce once Πλ>1/6 (Equation 11), these E. coli were able up to Πλ = 0.173 (Figure 5A). If Πλ>0.173, neither bacteria could reproduce, but damage accumulated and shut down division more slowly in cells with a = 0.4836 than a = ½ (Figure 5B).

Discussion
Just as deleterious mutations and selection create at equilibrium a mutational load, non-heritable damage and selection generate a damage load. Both type of loads contribute to the phenotypic load [18]. Analysis of a model for damage load in organisms dividing by fission revealed that a single fundamental parameter equal to Πλ determines equilibrium mean fitness , where the damage load is 1 − (see Table 1 for summary). Πλ is the product of two separate parameters in the model, λ the intrinsic damage rate and Π the doubling or life time of a damage-free individual. Thus, Πλ represents the total or lifetime damage rate of damage-free cell.
A damage load selects for mother cells that partition damage asymmetrically between daughters. If division were symmetrical, the daughters are identical and the equilibrium doubling time of descending lineages attains a real value when lifetime damage rate is less than 1/6 (Figure 1A). If the rate is greater 1/6, becomes infinitely long because the mother cells acquire too much damage and are unable to build cellular products to the amount needed for fission. The cell is alive but the lineage dies because doubling time becomes infinitely long (Figure 1B). Asymmetry allows cells to survive by division up to a rate less than 0.25 (see Transmission Rules; Figure 2; Table 1). Moreover, within the range of 0≤Πλ<0.25, equilibrium mean fitness is generally maximized as asymmetry decreases to the extreme when one daughter receives all of the damage harbored by a mother cell. Such extreme asymmetry is represented in the model with an asymmetry coefficient with a value of a = 0. However, for some intermediate lifetime damage rates an optimal and intermediate value of asymmetry is favored (Figure 3; Πλ = 0.17).
The evolution of asymmetry due to a damage load is comparable to the evolution of sex from a mutational load. The evolution of sex requires that the distribution of deleterious mutations is underdispersed in a population, i.e., that the variance is less than the mean [2]. Because sex shuffles genetic variation, its net effect is to redistribute mutations by a Poisson process, in which case the variance converges to the mean. If the variance and mean are equal, sex is not advantageous because the variance cannot be changed. If sexual reproduction were to overdisperse deleterious mutations an advantage can result, but that is prevented by the rules of genetic transmission. Asymmetry likewise increases variance in a population, but selection for asymmetry is much stronger because transmitting all or none of the damage to the daughters overdisperses the variance.
Asymmetrical transmission impacts the life history of a lineage by creating the two types of daughters. While daughter 1 is rejuvenated at birth, daughter 2 is loaded with damage. The deterioration of daughter 2, her daughter 2 in turn, and so forth constitutes currently one of the main hypothesis for the evolution of aging or senescence in microbes [11]–[14]. Fission in microbes results in the creation of a new and old pole. Because the new pole harbors less damage, it tags daughter 1. However, the long term consequences of asymmetry are debated. With symmetry and low damage, single-celled organisms are immortal (Figure 1A). Do high damage and asymmetry make them mortal [14], [19]–[22]? The model shows that it depends on the level of asymmetry and the rate of lifetime damage. If lifetime damage rate is less than 1/6 and asymmetry is sufficiently large, both the equilibrium doubling times and of daughters 1 and 2 attain real values and the microbe is immortal (Figure 2A). If the asymmetry is not sufficiently large, has a real equilibrium value, but becomes infinitely long and the daughter 2 lineage is mortal. The same outcome ensues if lifetime damage rates are greater than or equal to 1/6 and asymmetry is sufficiently small (Figure 2B). The mortality of daughter 2 renders all lineages in microbe mortal because all new poles eventually become old and reside in a daughter 2. Thus, although asymmetry matters, a lifetime damage rate of 1/6 is a key threshold. If the rate is less than 1/6, immortality is possible. If the rate is greater than or equal to 1/6, a microbe is mortal.
A recent study recording the division of E. coli cells over generations [14] provided an estimate of parameters for lifetime damage rate and asymmetry (see Estimating Model Parameters). The estimates placed E. coli in an area of the parameter space where the bacterium was immortal; both and attained real equilibrium values (Figure 4). However, the estimate of the asymmetry coefficient a at a value of 0.4836 was at first surprising. Given that fitness is generally maximized with extreme asymmetry (a = 0; Figure 3), a lower a could have been expected. What is the level of advantage provided by such a small degree of asymmetry? Could the level of asymmetry just be noise rather than an adaptation [22], [23]? If asymmetry is adaptive, why has it not evolved to be much higher? Resolution of these issues requires more information, but the current model can be used to provide guidance at this point.
On the basis of the parameter values estimated, the model predicts that the equilibrium mean fitness for an asymmetrical E. coli with a = 0.4836 is higher by a difference of 3×10−5 when compared to that of a hypothetical and symmetrical E. coli with a = ½ (Figure 5A). Although small, such a difference is more than sufficient for evolving asymmetry in large microbial populations. However, the difference may be on the low end of the range experienced by E. coli because the model was based on parameter values estimated in a benign laboratory environment. The parameter lifetime damage rate was estimated to be 0.1467, but it could be much higher for E. coli in the wild. If the rate were increased by 14% to the threshold of 1/6 (Equation 11), the advantage of a small degree of asymmetry is magnified. At this new rate, a symmetrical E. coli can no longer persist by reproduction and its doubling time becomes infinitely long (Figure 1B). With an asymmetry of just 0.4836, asymmetrical E. coli can persist up to rates as high as 0.173 (Figure 5A). Moreover, the advantage continues to increase if rates were further elevated. If they were greater than 0.173, E. coli with both a = 0.4836 and symmetry cannot persist, but damage accumulates and cell division shuts down more slowly in the asymmetrical bacterium. For example, if the rate were 0.175, the frequency of dividing cells drops to 0% in slightly over 500 min with symmetry, but only after more than 1300 min with a = 0.4836 (Figure 5B). Retaining a few dividing cells for several extra hundred minutes could be invaluable to an organism capable of rapid growth. Thus, the fitness advantage of a small degree of asymmetry, such as a = 0.4836, could be high.
However, why has asymmetry level in E. coli not evolved to be higher than 0.4836? An obvious answer is there may be a cost. Although the model assumes no costs, it reveals the fitness constraints. Assuming that E. coli experiences a higher lifetime damage rate of 0.17, inspection of Figure 3 shows that the equilibrium mean fitness has the greatest curvature when asymmetry equals 0.475. Equilibrium mean fitness equals 0.68 when asymmetry is 0.475 and it increases only by 3% to 0.70 when asymmetry is 0.450. If in the simplest scenario the cost of reducing a from ½ to 0.475 equals from 0.475 to 0.450, fitness gain for the second reduction could be too small to override the costs. The fitness gain for the first reduction is large because symmetrical bacteria cannot reproduce when the lifetime damage rate is 0.17 (Figure 3; Table 1). Unless the cost is extremely small or the second reduction is less costly, asymmetry should evolve to reside where the curvature is greatest [24]. The level of asymmetry can be shifted by different cost functions, but the curvature constrains its evolution to the neighborhood of 0.475. Estimating the costs will be needed for a full resolution, but the low asymmetry estimated for E. coli may well be anticipated by the model.
A higher lifetime damage rate may be reasonable for E. coli and other microbes. Defenses and weapons by microbial competitors and hosts routinely employ mechanisms that inflict non-genetic damage often through oxidation [25]–[29]. Microbes face damage even in apparently benign environments. E. coli grown under standard laboratory conditions do not experience much oxidative damage. However, 48 hr after reaching stasis, oxidative damage to proteins increases six fold [30]. The damaged population can be separated into two fractions by centrifugation. One fraction, which accounts for 40% of the cells, contains bacteria capable of dividing and forming colonies on agar plates. The bacteria in the second fraction are not, although they remain intact and metabolically active. Most importantly, almost 90% of the detectable oxidative damage is in the second fraction, which demonstrates well outcomes comparable to Figure 2A and Figure 5B.
Because a damage load is created by non-heritable variation, it has characteristics that are attributable to the soma. The asymmetrical transmission of non-heritable damage in microbes, and the subsequent division of labor [31], has led to suggestions that these organisms have the equivalent of soma and germline [21],[32]. From this perspective, the evolution of germline, soma, and senescence in metazoans [32] is just the extension of microbial asymmetry and the damage load could be called the somatic load. Although the present model was formulated for microbes, it could be generalized to include metazoans. It may also be useful for describing a population of cells within a metazoan. Do stem cells partition damage asymmetrically?
Many aspects of the present model are not novel. Previous models have shown that the asymmetrical transmission of damage can be favored during binary fission by both directional and stabilizing selection [8]–[10]. Erjavec et al. [11] demonstrated qualitatively with simulations a threshold for cells dividing symmetrically. However, the present model offers some new perspectives. First, the derivation of a damage load allows a comparison to a mutational load. In metazoans with large genomes, the mutational load [33] could be as large as some of the damage load estimates (Figure 3). On the other hand, because the mutational load is smaller in microbes [33], the damage load could be a stronger evolutionary force. Second, the present model shows that the two parameters Π and λ combine to form a single fundamental parameter as the product Πλ or the lifetime damage rate. Moreover, the model was also able to predict key thresholds for Πλ at 1/6 and 0.25 without any empirical/data calibration. The threshold of 1/6 delineates the boundary for when cell dividing by fission is mortal or immortal. This outcome stands in contrast to the absence of any theoretical framework for whether the genomic mutation rate U, a key parameter for determining the mutational load (Equation 1) has an upper limit, despite the fact that metazoans and RNA viruses have independently evolved maximum rates of 1 (reference [33]). Third, a fit of the model to experimental data from E. coli provided estimates for all of the key parameters in the model. The parameter values showed that E. coli was immortal under the conditions examined. The determination of where a real organism resides in parameter space offers a powerful predictive tool for studying evolution.
Zdroje
1. HaldaneJBS
1937 The Effect of Variation of Fitness. The American Naturalist 71 337 349
2. KondrashovAS
1993 Classification of Hypotheses on the Advantage of Amphimixis. Journal of Heredity 84 372 387
3. MullerHJ
1950 Our Load of Mutations. American Journal of Human Genetics 2 111 176
4. CrowJF
1958 Some possibilities for measuring -selection intensities in man. Human Biol 30 1 13
5. KimuraM
MaruyamaT
1966 Mutational Load with Epistatic Gene Interactions in Fitness. Genetics 54 1337 1351
6. OhtaT
1973 Slightly Deleterious Mutant Substitutions in Evolution. Nature 246 96 98
7. CharlesworthB
CharlesworthD
1998 Some evolutionary consequences of deleterious mutations. Genetica 103 3 19
8. AckermannM
ChaoL
BergstromCT
DoebeliM
2007 On the evolutionary origin of aging. Aging Cell 6 235 244
9. EvansSN
SteinsaltzD
2007 Damage segregation at fissioning may increase growth rates: A superprocess model. Theoretical Population Biology 71 473 490
10. WatveM
ParabS
JogdandP
KeniS
2006 Aging may be a conditional strategic choice and not an inevitable outcome for bacteria. Proc Natl Acad Sci U S A 103 14831 14835
11. ErjavecN
CvijovicM
KlippE
NystromT
2008 Selective benefits of damage partitioning in unicellular systems and its effects on aging. Proc Natl Acad Sci U S A 105 18764 18769
12. AckermannM
StearnsSC
JenalU
2003 Senescence in a bacterium with asymmetric division. Science 300 1920 1920
13. LindnerAB
MaddenR
DemarezA
StewartEJ
TaddeiF
2008 Asymmetric segregation of protein aggregates is associated with cellular aging and rejuvenation. Proc Natl Acad Sci U S A 105 3076 3081
14. StewartEJ
MaddenR
PaulG
TaddeiF
2005 Aging and death in an organism that reproduces by morphologically symmetric division. Plos Biology 3 e45 doi:10.1371/journal.pbio.0030045
15. BoyeE
NordstromK
2003 Coupling the cell cycle to cell growth - A look at the parameters that regulate cell-cycle events. Embo Reports 4 757 760
16. VinellaD
DariR
1995 Overview of Controls in the Escherichia-Coli Cell-Cycle. Bioessays 17 527 536
17. PondSLK
FrostSDW
MuseSV
2005 HyPhy: hypothesis testing using phylogenies. Bioinformatics 21 676 679
18. O'DonaldP
1968 Measuring the intensity of natural selection. Nature 220 197 198
19. KirkwoodTB
2005 Asymmetry and the origins of ageing. Mech Ageing Dev 126 533 534
20. FerberD
2005 Microbiology. Immortality dies as bacteria show their age. Science 307 656
21. NystromT
2002 Aging in bacteria. Curr Opin Microbiol 5 596 601
22. WoldringhCL
2005 Is Escherichia coli getting old? Bioessays 27 770 774
23. StewartE
TaddeiF
2005 Aging in Esherichia coli: signals in the noise. Bioessays 27 983
24. CharnovEL
1976 Optimal Foraging, Marginal Value Theorem. Theoretical Population Biology 9 129 136
25. GrossL
2007 Paradox Resolved? The Strange Case of the Radiation-Resistant Bacteria. PLoS Biology 5 e108 doi:10.1371/journal.pbio.0050108
26. LambethJD
2004 NOX enzymes and the biology of reactive oxygen. Nat Rev Immunol 4 181 189
27. ParkB
NizetV
LiuGY
2008 Role of Staphylococcus aureus catalase in niche competition against Streptococcus pneumoniae. J Bacteriol 190 2275 2278
28. DukanS
FarewellA
BallesterosM
TaddeiF
RadmanM
2000 Protein oxidation in response to increased transcriptional or translational errors. Proc Natl Acad Sci U S A 97 5746 5749
29. DokeN
MiuraY
SanchezLM
ParkHJ
NoritakeT
1996 The oxidative burst protects plants against pathogen attack: mechanism and role as an emergency signal for plant bio-defence–a review. Gene 179 45 51
30. DesnuesB
CunyC
GregoriG
DukanS
AguilaniuH
2003 Differential oxidative damage and expression of stress defence regulons in culturable and non-culturable Escherichia coli cells. EMBO Rep 4 400 404
31. KirkwoodTB
2005 Understanding the odd science of aging. Cell 120 437 447
32. TurkePW
2008 Williams's theory of the evolution of senescence: Still useful at fifty. Quarterly Review of Biology 83 243 256
33. DrakeJW
CharlesworthB
CharlesworthD
CrowJF
1998 Rates of spontaneous mutation. Genetics 148 1667 1686
34. MayRM
1976 Simple Mathematical-Models with Very Complicated Dynamics. Nature 261 459 467
Štítky
Genetika Reprodukční medicínaČlánek vyšel v časopise
PLOS Genetics
2010 Číslo 8
- Souvislost haplotypu M2 genu pro annexin A5 s opakovanými reprodukčními ztrátami
- Akutní intermitentní porfyrie
- IVF a rakovina prsu – zvyšují hormony riziko vzniku rakoviny?
- GHC Genetics – léty prověřený partner českých lékařů v oblasti genetiky
- Růst a vývoj dětí narozených pomocí IVF
Nejčtenější v tomto čísle
- Identification of the Bovine Arachnomelia Mutation by Massively Parallel Sequencing Implicates Sulfite Oxidase (SUOX) in Bone Development
- Common Inherited Variation in Mitochondrial Genes Is Not Enriched for Associations with Type 2 Diabetes or Related Glycemic Traits
- A Model for Damage Load and Its Implications for the Evolution of Bacterial Aging
- Did Genetic Drift Drive Increases in Genome Complexity?

