-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaA Missing Dimension in Measures of Vaccination Impacts
article has not abstract
Published in the journal: . PLoS Pathog 10(3): e32767. doi:10.1371/journal.ppat.1003849
Category: Opinion
doi: https://doi.org/10.1371/journal.ppat.1003849Summary
article has not abstract
Immunological protection, acquired from either natural infection or vaccination, varies among hosts, reflecting underlying biological variation and affecting population-level protection. Owing to the nature of resistance mechanisms, distributions of susceptibility and protection entangle with pathogen dose in a way that can be decoupled by adequately representing the dose dimension. Any infectious processes must depend in some fashion on dose, and empirical evidence exists for an effect of exposure dose on the probability of transmission to mumps-vaccinated hosts [1], the case-fatality ratio of measles [2], and the probability of infection and, given infection, of symptoms in cholera [3]. Extreme distributions of vaccine protection have been termed leaky (partially protects all hosts) and all-or-nothing (totally protects a proportion of hosts) [4]. These distributions can be distinguished in vaccine field trials from the time dependence of infections [5]. Frailty mixing models have also been proposed to estimate the distribution of protection from time to event data [6], [7], although the results are not comparable across regions unless there is explicit control for baseline transmission [8]. Distributions of host susceptibility and acquired protection can be estimated from dose-response data generated under controlled experimental conditions [9]–[11] and natural settings [12], [13]. These distributions can guide research on mechanisms of protection, as well as enable model validity across the entire range of transmission intensities. We argue for a shift to a dose-dimension paradigm in infectious disease science and community health.
Natural Transmission
We consider a minimal susceptible (S) and infected (I) model [14] of pathogen transmission in a host population to explore population effects of protection conferred by a vaccine (or other preventive measure, such as symbionts) against infection, under different assumptions about how this is distributed among individuals. We consider that infection is lifelong, and that there is no naturally acquired immunity.
Vaccines that provide leaky protection against infection act by reducing susceptibility to a factor σ that is distributed among individuals according to a probability density function , where . Denoting by the densities of hosts who are vaccinated and have susceptibility factor , the integral represents the proportion of hosts who are infected despite being vaccinated. Assuming no effect on infectiousness, the per capita rate of infection among totally susceptible individuals is given by , where β is the effective contact rate.
Figure 1A shows, for the distributions represented on the right, equilibrium curves describing prevalence of infection versus transmission intensity measured by , the basic reproduction number. The curves for extreme cases of vaccines that confer equal protection to all or total protection to some and none to others are depicted by the higher (red) and lower (blue) curves, respectively. Intermediate curves represent scenarios in which susceptibility follows a beta distribution with fixed mean and increasing variance from top to bottom. Prevalence curves become shallower with heterogeneity and converge to the same level as transmission increases, except in the all-or-nothing extreme, in which the prevalence cannot surpass the susceptible fraction, irrespective of transmission intensity. Although the impact of protection appears to increase with polarization of effects, the endemic curves do not converge uniformly to their all-or-nothing homologue. In the absence of unequivocal empirical evidence for the idealized all-or-nothing mode of action, we suggest modifying the terminology to include polarized distributions more generally.
Fig. 1. Decreasing infection with heterogeneity in host protection. 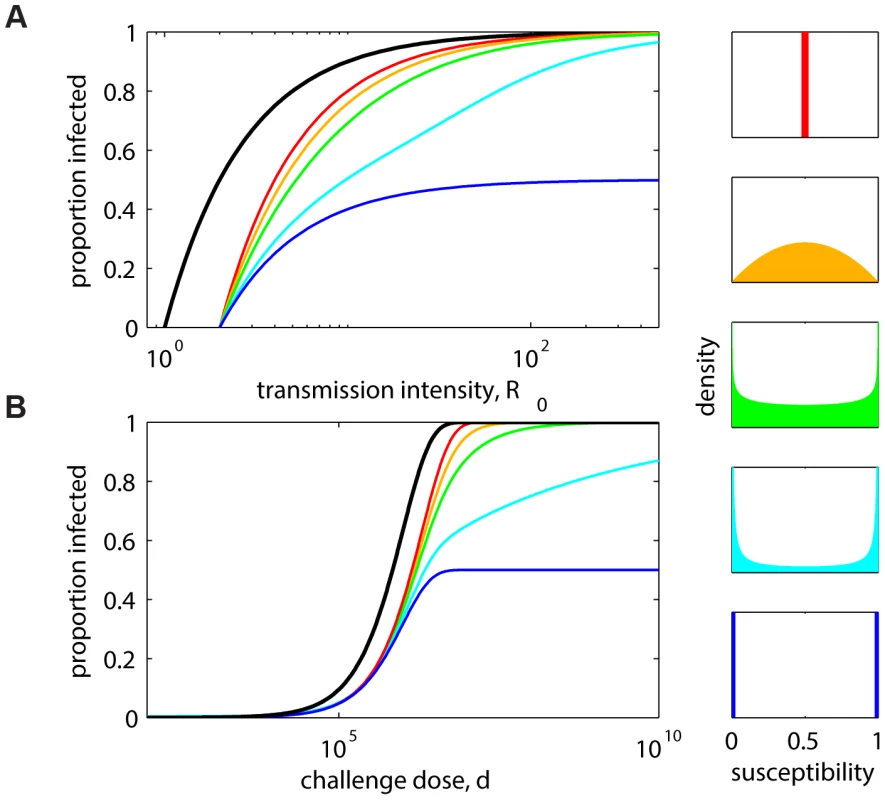
(A) Equilibrium prevalence of infection under a pathogen transmission model in which an intervention (vaccine or symbiont) reduces host susceptibility to a factor that is distributed as specified. The model is formally represented by the rates of change in the proportions of the population that are susceptible and infected: , , , and , where S and I are nonintervention, while and are intervention groups with susceptibility x distributed as (right panels). Colored lines assume total intervention coverage (), while the black line represents the scenario without intervention (). (B) Dose-response curves expected from an experiment in which groups of naive (black) and intervention (colored) hosts are challenged with a range of pathogen doses, under a model in which the intervention reduces susceptibility to a factor that is distributed as in panels on the right. Models for infected proportions in nonintervention and intervention groups are formalized in a dose-response manner by and , respectively, where d is the number of pathogens the host is challenged by and p is the probability of infection for each pathogen. Colored lines assume susceptibility factors distributed with mean 0.5 in all cases and variance 0 (red), 0.05 (orange), 0.1 (green), 0.2 (cyan), and 0.25 (blue). Red and blue at the extremes are discrete, while the intermediate cases are continuous beta distributions, with shape parameters a and b such that the mean is fixed,, and the variance, , spans the range, . Transmission models assume , and controlled infection models assume . This illustration indicates that the distribution of vaccine effects among individuals is a major determinant of population-level impact and should be considered in evaluation. Specifically, the more homogeneously a vaccine acts, the lower its impact on disease transmission. Measures based on multipopulation study designs, spanning a range of transmission intensities, enable the inference of such distributions.
Experimental Challenge
Infection in a controlled experimental setting is modeled by describing infected proportions in terms of challenge dose. Adopting standard formulations [15]–[17], the mean number of infecting pathogens is, where d is the number of pathogens challenging the host, and p is the probability of infection for each pathogen; the number of infecting pathogens per host has a Poisson distribution with mean . In the homogeneous case, the probability of a host remaining uninfected after pathogen challenge is the zero term of the distribution, leading to a probability of infection, represented by the black curve in Figure 1B.
This model fails to fit many experimental data sets in which groups of hosts are exposed to varying doses of the pathogen, and the proportion infected in each group is calculated. In particular, the slope of the curve implied by this model is steeper than what is often observed. However, if individual hosts vary in their susceptibility to infection, a reduced slope arises. A simple model [11] assumes that the probability of each particle causing infection varies among hosts according to a beta distribution , akin to the vaccine protection factor above, resulting in the modified dose-response .
Figure 1B illustrates dose-infectivity curves expected from an experiment in which groups of naive and vaccinated hosts are challenged with a range of pathogen doses under the distributions of protection described above, uncovering again a lack of uniform convergence to the all-or-nothing formulation.
We have adopted the same notation, , for susceptibility distributions in both natural transmission and experimental challenge settings to indicate the linkage between two arms of a unified study, as advocated here.
Classification of Intervention Effects
Experimental dose-infectivity curves provide information to infer the mode of action of interventions, such as vaccines. Given the lack of uniform convergence to all-or-nothing as the leaky mode becomes increasingly polarized, we have classified beta distribution shapes according to polarization (Figure 2). The dashed line along the diagonal indicates the location of the symmetric distributions used in Figure 1, and the circles indicate the location of the extreme homogeneous (red) and all-or-nothing (blue) distributions. The power to identify polarized distributions is analyzed in Figure S1, focusing on a vicinity of the uniform shape (gray square), showing good discriminatory power in the region of parameter space where uncertainty is greatest. This analysis suggests a promising approach for classifying intervention effects in controlled experimental settings and using this as prior information for further study in natural settings [18].
Fig. 2. Shape classification in the terms of parameters a and b. 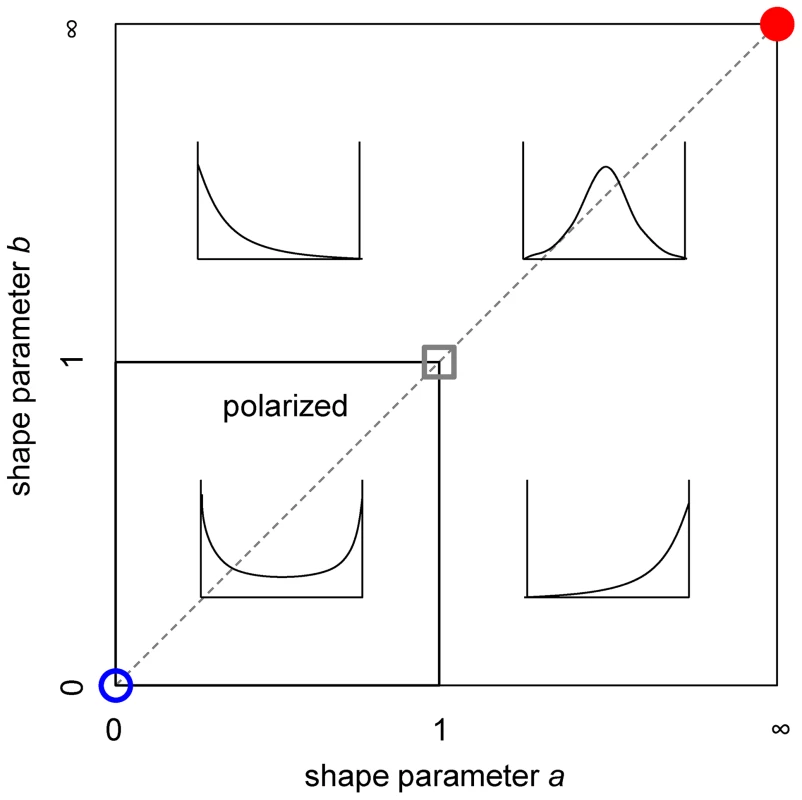
Beta distributions are classified as: polarized if ; symmetric if (gray dashed line), as in Figure 1; homogeneous in the limit (red circle), as red in Figure 1; all-or-nothing in the limit (blue circle), as blue in Figure 1; and uniform if (gray square). The power to identify polarized distributions is analyzed in a neighborhood of the uniform distribution (Figure S1). Supporting Information
Zdroje
1. BarskeyAE, Cynthia SchulteC, RosenJB, HandschurEF, Rausch-PhungE, et al. (2012) Mumps Outbreak in Orthodox Jewish Communities in the United States. N Engl J Med 367 : 1704–1713.
2. AabyP, BukhJ, LisseIM, SmithsAJ (1984) Overcrowding and intensive exposure as determinants of measles mortality. Am J Epidemiol 120 : 49–63.
3. HornickRB, MusicSI, WenzelR, CashR, LibonatiJP, et al. (1971) The Broad Street pump revisited: Response of volunteers to ingested cholera vibrios. Bull N Y Acad Med 47 : 1181–1191.
4. Halloran ME, Longini IM Jr, Struchiner CJ (2010) Design and Analysis of Vaccine Studies. New York: Springer.
5. SmithPG, RodriguesLC, FinePE (1984) Assessment of the protective efficacy of vaccines against common diseases using case-control and cohort studies. Int J Epidemiol 13 : 87–93.
6. HalloranME, LonginiIMJr, StruchinerCJ (1996) Estimability and interpretability of vaccine efficacy using frailty mixing models. Am J Epidemiol 144 : 83–97.
7. LonginiIMJr, HalloranME (1996) A frailty mixture model for estimating vaccine efficacy. Appl Statist 45 : 165–173.
8. StruchinerCJ, HalloranME (2007) Randomization and baseline transmission in vaccine field trials. Epidemiol Infect 135 : 181–194.
9. FurumotoWA, MickeyR (1967) A mathematical model for the infectivity-dilution curve of tobacco mosaic virus: Theoretical consideration. Virology 32 : 216–223.
10. FurumotoWA, MickeyR (1967) A mathematical model for the infectivity-dilution curve of tobacco mosaic virus: Experimental tests. Virology 32 : 224–233.
11. Haas CN, Rose JB, Gerba CP (1999) Quantitative Microbial Risk Assessment. New York: John Wiley & Sons, Inc.
12. SmithDL, DushoffJ, SnowRW, HaySI (2005) The entomological inoculation rate and Plasmodium falciparum infection in African children. Nature 438 : 492–495.
13. GomesMGM, AguasR, LopesJS, NunesMC, RebeloC, et al. (2012) How host selection governs tuberculosis reinfection. Proc R Soc B 279 : 2473–2478.
14. Keeling MJ, Rohani P (2008) Modeling Infectious Diseases in Humans and Animals. New Jersey: Princeton University Press.
15. DruettHA (1952) Bacterial invasion. Nature 170 : 288.
16. Ben-AmiF, RegoesRR, EbertD (2008) A quantitative test of the relationship between parasite dose and infection probability across different host-parasite combinations. Proc R Soc B 275 : 853–859.
17. ZwartMP, HemerikL, CoryJS, de VisserJAGM, BianchiFJJA, et al. (2011) An experimental text of the independent action hypothesis in virus-insect pathosystems. Proc R Soc B 276 : 2233–2242.
18. DwyerG, ElkintonJS, BuonaccorsiJP (1997) Host heterogeneity in susceptibility and disease dynamics: Tests of a mathematical model. Am Nat 150 : 685–707.
Štítky
Hygiena a epidemiologie Infekční lékařství Laboratoř
Článek DHX36 Enhances RIG-I Signaling by Facilitating PKR-Mediated Antiviral Stress Granule FormationČlánek Oral Bacteria and CancerČlánek A Non-Coding RNA Promotes Bacterial Persistence and Decreases Virulence by Regulating a Regulator in
Článek vyšel v časopisePLOS Pathogens
Nejčtenější tento týden
2014 Číslo 3- Jak souvisí postcovidový syndrom s poškozením mozku?
- Stillova choroba: vzácné a závažné systémové onemocnění
- Perorální antivirotika jako vysoce efektivní nástroj prevence hospitalizací kvůli COVID-19 − otázky a odpovědi pro praxi
- Diagnostika virových hepatitid v kostce – zorientujte se (nejen) v sérologii
- Diagnostický algoritmus při podezření na syndrom periodické horečky
-
Všechny články tohoto čísla
- Conflicting Interests in the Pathogen–Host Tug of War: Fungal Micronutrient Scavenging Versus Mammalian Nutritional Immunity
- Putting Fungi to Work: Harvesting a Cornucopia of Drugs, Toxins, and Antibiotics
- Mycobacteriophages: Windows into Tuberculosis
- Human African Trypanosomiasis and Immunological Memory: Effect on Phenotypic Lymphocyte Profiles and Humoral Immunity
- Five Things to Know about Genetically Modified (GM) Insects for Vector Control
- A Missing Dimension in Measures of Vaccination Impacts
- Eosinophils Are Important for Protection, Immunoregulation and Pathology during Infection with Nematode Microfilariae
- Clonality of HTLV-2 in Natural Infection
- Production, Fate and Pathogenicity of Plasma Microparticles in Murine Cerebral Malaria
- Group B Streptococcal Infection of the Choriodecidua Induces Dysfunction of the Cytokeratin Network in Amniotic Epithelium: A Pathway to Membrane Weakening
- New Insights into How Adapts to Its Mammalian Host during Bubonic Plague
- Foodborne Transmission of Nipah Virus in Syrian Hamsters
- A Polysaccharide Virulence Factor from Elicits Anti-inflammatory Effects through Induction of Interleukin-1 Receptor Antagonist
- Structural and Functional Characterization of a Complex between the Acidic Transactivation Domain of EBNA2 and the Tfb1/p62 Subunit of TFIIH
- Adaptive Gene Amplification As an Intermediate Step in the Expansion of Virus Host Range
- DHX36 Enhances RIG-I Signaling by Facilitating PKR-Mediated Antiviral Stress Granule Formation
- Hepatitis B Virus Infection and Immunopathogenesis in a Humanized Mouse Model: Induction of Human-Specific Liver Fibrosis and M2-Like Macrophages
- Crk Adaptors Negatively Regulate Actin Polymerization in Pedestals Formed by Enteropathogenic (EPEC) by Binding to Tir Effector
- Fatty Acid Biosynthesis Contributes Significantly to Establishment of a Bioenergetically Favorable Environment for Vaccinia Virus Infection
- A Cytosolic Chaperone Complexes with Dynamic Membrane J-Proteins and Mobilizes a Nonenveloped Virus out of the Endoplasmic Reticulum
- Intracellular Promote Invasive Cell Motility through Kinase Regulation of the Host Actin Cytoskeleton
- MAVS-MKK7-JNK2 Defines a Novel Apoptotic Signaling Pathway during Viral Infection
- RON5 Is Critical for Organization and Function of the Moving Junction Complex
- Immune Suppression by Neutrophils in HIV-1 Infection: Role of PD-L1/PD-1 Pathway
- and Exhibit Metabolic Symbioses
- The Herpes Virus Fc Receptor gE-gI Mediates Antibody Bipolar Bridging to Clear Viral Antigens from the Cell Surface
- Target Cell Availability, Rather than Breast Milk Factors, Dictates Mother-to-Infant Transmission of SIV in Sooty Mangabeys and Rhesus Macaques
- Evolution of the Retroviral Restriction Gene : Inhibition of Non-MLV Retroviruses
- Infection of Adult Thymus with Murine Retrovirus Induces Virus-Specific Central Tolerance That Prevents Functional Memory CD8 T Cell Differentiation
- Fha Interaction with Phosphothreonine of TssL Activates Type VI Secretion in
- In Vivo Administration of a JAK3 Inhibitor during Acute SIV Infection Leads to Significant Increases in Viral Load during Chronic Infection
- Lack of Detectable HIV-1 Molecular Evolution during Suppressive Antiretroviral Therapy
- Activation of HIV-1 from Latent Infection via Synergy of RUNX1 Inhibitor Ro5-3335 and SAHA
- A Compact, Multifunctional Fusion Module Directs Cholesterol-Dependent Homomultimerization and Syncytiogenic Efficiency of Reovirus p10 FAST Proteins
- The Role of Host and Microbial Factors in the Pathogenesis of Pneumococcal Bacteraemia Arising from a Single Bacterial Cell Bottleneck
- Genetic Dissection of Gut Epithelial Responses to
- Two-Component System Cross-Regulation Integrates Response to Heme and Cell Envelope Stress
- Oral Mycobiome Analysis of HIV-Infected Patients: Identification of as an Antagonist of Opportunistic Fungi
- A Model System for Studying the Transcriptomic and Physiological Changes Associated with Mammalian Host-Adaptation by Serovar Copenhageni
- Inflammasome Sensor NLRP1 Controls Rat Macrophage Susceptibility to
- ChIP-Seq and RNA-Seq Reveal an AmrZ-Mediated Mechanism for Cyclic di-GMP Synthesis and Biofilm Development by
- The Hypervariable Amino-Terminus of P1 Protease Modulates Potyviral Replication and Host Defense Responses
- Caspase-1-Dependent and -Independent Cell Death Pathways in Infection of Macrophages
- The Effect of Cell Growth Phase on the Regulatory Cross-Talk between Flagellar and Spi1 Virulence Gene Expression
- Different Mutagenic Potential of HIV-1 Restriction Factors APOBEC3G and APOBEC3F Is Determined by Distinct Single-Stranded DNA Scanning Mechanisms
- Oral Bacteria and Cancer
- Identification of OmpA, a Protein Involved in Host Cell Invasion, by Multi-Phenotypic High-Content Screening
- Transovarial Transmission of a Plant Virus Is Mediated by Vitellogenin of Its Insect Vector
- VE-Cadherin Cleavage by LasB Protease from Facilitates Type III Secretion System Toxicity in Endothelial Cells
- Dimerization of VirD2 Binding Protein Is Essential for Induced Tumor Formation in Plants
- Crystal Structure of the Vaccinia Virus DNA Polymerase Holoenzyme Subunit D4 in Complex with the A20 N-Terminal Domain
- Post-Translational Regulation via Clp Protease Is Critical for Survival of
- Modulation of Phagosomal pH by Promotes Hyphal Morphogenesis and Requires Stp2p, a Regulator of Amino Acid Transport
- Rotavirus Activates Lymphocytes from Non-Obese Diabetic Mice by Triggering Toll-Like Receptor 7 Signaling and Interferon Production in Plasmacytoid Dendritic Cells
- Cytomegalovirus m154 Hinders CD48 Cell-Surface Expression and Promotes Viral Escape from Host Natural Killer Cell Control
- Interferon Regulatory Factor-1 Protects from Fatal Neurotropic Infection with Vesicular Stomatitis Virus by Specific Inhibition of Viral Replication in Neurons
- HMGB1-Promoted and TLR2/4-Dependent NK Cell Maturation and Activation Take Part in Rotavirus-Induced Murine Biliary Atresia
- An Immunomics Approach to Schistosome Antigen Discovery: Antibody Signatures of Naturally Resistant and Chronically Infected Individuals from Endemic Areas
- PPARγ Agonists Improve Survival and Neurocognitive Outcomes in Experimental Cerebral Malaria and Induce Neuroprotective Pathways in Human Malaria
- A Non-Coding RNA Promotes Bacterial Persistence and Decreases Virulence by Regulating a Regulator in
- Viral OTU Deubiquitinases: A Structural and Functional Comparison
- Heterogeneity and Breadth of Host Antibody Response to KSHV Infection Demonstrated by Systematic Analysis of the KSHV Proteome
- Influenza A Virus Assembly Intermediates Fuse in the Cytoplasm
- Broadly Reactive Human CD8 T Cells that Recognize an Epitope Conserved between VZV, HSV and EBV
- Oncogenic Human Papillomaviruses Activate the Tumor-Associated Lens Epithelial-Derived Growth Factor (LEDGF) Gene
- Erythrocyte Invasion: Combining Function with Immune Evasion
- IL-1α and Complement Cooperate in Triggering Local Neutrophilic Inflammation in Response to Adenovirus and Eliminating Virus-Containing Cells
- Chronic Exposure to Type-I IFN under Lymphopenic Conditions Alters CD4 T Cell Homeostasis
- PLOS Pathogens
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Cytomegalovirus m154 Hinders CD48 Cell-Surface Expression and Promotes Viral Escape from Host Natural Killer Cell Control
- Human African Trypanosomiasis and Immunological Memory: Effect on Phenotypic Lymphocyte Profiles and Humoral Immunity
- DHX36 Enhances RIG-I Signaling by Facilitating PKR-Mediated Antiviral Stress Granule Formation
- Conflicting Interests in the Pathogen–Host Tug of War: Fungal Micronutrient Scavenging Versus Mammalian Nutritional Immunity
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání



