-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaUsing Extended Genealogy to Estimate Components of Heritability for 23 Quantitative and Dichotomous Traits
Important knowledge about the determinants of complex human phenotypes can be obtained from the estimation of heritability, the fraction of phenotypic variation in a population that is determined by genetic factors. Here, we make use of extensive phenotype data in Iceland, long-range phased genotypes, and a population-wide genealogical database to examine the heritability of 11 quantitative and 12 dichotomous phenotypes in a sample of 38,167 individuals. Most previous estimates of heritability are derived from family-based approaches such as twin studies, which may be biased upwards by epistatic interactions or shared environment. Our estimates of heritability, based on both closely and distantly related pairs of individuals, are significantly lower than those from previous studies. We examine phenotypic correlations across a range of relationships, from siblings to first cousins, and find that the excess phenotypic correlation in these related individuals is predominantly due to shared environment as opposed to dominance or epistasis. We also develop a new method to jointly estimate narrow-sense heritability and the heritability explained by genotyped SNPs. Unlike existing methods, this approach permits the use of information from both closely and distantly related pairs of individuals, thereby reducing the variance of estimates of heritability explained by genotyped SNPs while preventing upward bias. Our results show that common SNPs explain a larger proportion of the heritability than previously thought, with SNPs present on Illumina 300K genotyping arrays explaining more than half of the heritability for the 23 phenotypes examined in this study. Much of the remaining heritability is likely to be due to rare alleles that are not captured by standard genotyping arrays.
Published in the journal: . PLoS Genet 9(5): e32767. doi:10.1371/journal.pgen.1003520
Category: Research Article
doi: https://doi.org/10.1371/journal.pgen.1003520Summary
Important knowledge about the determinants of complex human phenotypes can be obtained from the estimation of heritability, the fraction of phenotypic variation in a population that is determined by genetic factors. Here, we make use of extensive phenotype data in Iceland, long-range phased genotypes, and a population-wide genealogical database to examine the heritability of 11 quantitative and 12 dichotomous phenotypes in a sample of 38,167 individuals. Most previous estimates of heritability are derived from family-based approaches such as twin studies, which may be biased upwards by epistatic interactions or shared environment. Our estimates of heritability, based on both closely and distantly related pairs of individuals, are significantly lower than those from previous studies. We examine phenotypic correlations across a range of relationships, from siblings to first cousins, and find that the excess phenotypic correlation in these related individuals is predominantly due to shared environment as opposed to dominance or epistasis. We also develop a new method to jointly estimate narrow-sense heritability and the heritability explained by genotyped SNPs. Unlike existing methods, this approach permits the use of information from both closely and distantly related pairs of individuals, thereby reducing the variance of estimates of heritability explained by genotyped SNPs while preventing upward bias. Our results show that common SNPs explain a larger proportion of the heritability than previously thought, with SNPs present on Illumina 300K genotyping arrays explaining more than half of the heritability for the 23 phenotypes examined in this study. Much of the remaining heritability is likely to be due to rare alleles that are not captured by standard genotyping arrays.
Introduction
Although genome-wide association studies (GWAS) have resulted in the discovery of thousands of novel associations of loci to hundreds of phenotypes [1], concerns have been raised about the finding that these loci appear to explain a relatively small proportion of the estimated heritability, the fraction of phenotypic variation in a population that is due to genetic variation [2]. This has led to considerable speculation by researchers about the genetic basis of complex human phenotypes and the “missing heritability”, i.e. the fraction of heritability not accounted for by the associations discovered to date [3], [4], [5], [6], [7], [8], [9]. Among the proposed explanations for missing heritability is the existence of many presently unidentified common variants with small effect sizes, rare variants not captured by current genotyping platforms, structural variants, epistatic interactions, gene-environment interactions, parent-of-origin effects, or inflated heritability estimates [3], [5], [10]. Studies that examine the sources of missing heritability can help researchers to evaluate the prospects of future studies focusing on common versus rare variation and thereby devise effective strategies to discover the remaining sequence variants that affect disease risk and other aspects of phenotypic variation in humans.
The narrow-sense heritability of a phenotype () is the fraction of phenotypic variance that can be described by an additive model over the set of SNPs that are functionally related to the phenotype (i.e. the causal SNPs) [11]. It is commonly estimated by comparing the phenotypic correlation of monozygotic (MZ) to that of dizygotic (DZ) twins. The difference between and the fraction of phenotypic variance accounted for by variants discovered by means of GWAS () is the so-called missing heritability. Recently, Yang et al [12] developed a method to estimate the variance explained by all SNPs on a genotyping platform including those that are not genome-wide significant (), representing the limit of for infinite sample size.
There are two major challenges in comparing and to quantify missing heritability. First, there is the potential for inflation of estimates based on closely related individuals such as MZ/DZ twins. It is well known that epistatic interactions can inflate heritability estimates in studies of related individuals [13]. Recent work from Zuk et al [10] has examined this in detail. Other factors that could also lead to inflated estimates of using closely related pairs of individuals include dominance and shared environment. Second, there is a tradeoff between inflation and sampling variance when estimating . The recent variance component approach described by Yang et. al results in inflated estimates of in the presence of related individuals [12], [14], [15], [16], [17]. However, removing related individuals reduces the sample size, resulting in a larger standard error around the estimate [18], [19]. Both of these issues can adversely affect estimates of missing heritability.
Here, we analyze the heritability of 23 complex phenotypes in an Icelandic cohort of 38,167 individuals, leveraging both a population-wide genealogical database and genotype data from over 300,000 SNPs that have been long-range phased across and between chromosomes (i.e. where not only the phase, but also the parental origin of alleles has been determined) [20]. Importantly, we develop an approach that allows to be estimated on the basis of both closely and distantly related pairs of individuals. We find, for all of the quantitative phenotypes, that our estimates of are smaller than those from the literature that were based on MZ/DZ twins [21]. Our results indicate that previous estimates were inflated by the impact of epistasis or shared environment.
We further introduce a new variance components method that provides simultaneous estimates of and . This method has two principal advantages. First, by adequately taking account of both closely and distantly related pairs of individuals, it minimizes the standard error of the estimates, whilst avoiding the upward bias that can result from calculations based on closely related pairs. Second, it produces both estimates of heritability for the same population sample, ensuring that and are directly comparable.
For most of the 23 phenotypes examined here, our results show that accounts for more than half of . As GWAS have not identified many SNPs with large effect sizes (i.e. is small), and is greater than by a considerable margin, it follows that there must be many associated sequence variants that remain to be discovered, i.e. these phenotypes are highly polygenic. Currently, only common variants are well captured by the genotyping arrays used in most GWAS studies. As the difference between and is likely due to common and rare variants not captured by the genotyping array [12], it may be assumed that a fair number of association signals remain to be identified through more comprehensive approaches, such as whole genome-sequencing. However, our estimates of show that GWAS genotyping arrays capture a greater proportion of than indicated by previous twin-based estimates of .
Results
Overview of methods
Below, we provide an overview of the approaches we used to estimate various components of heritability. The details of these approaches are provided in the Methods section.
We used a linear mixed model approach to estimate components of heritability. In this approach, each phenotype is modeled using a multivariate normal distribution. Each of the components of heritability that we estimated corresponds to a different model of the phenotypic covariance.
Narrow-sense heritability () estimates from variance component models rely on covariance matrices specifying the genome-wide genetic relatedness of individuals in the data set. An estimate of can be obtained by using an identity-by-descent (IBD) based covariance matrix, which is trivial to obtain from long-range phased genotype data (see below).
The fine-scale estimates of IBD used here rely on long-range phasing data that are not available in most data sets. An estimate of can also be obtained by using an identity-by-state with threshold (IBS>t) based covariance matrix with all values below a threshold t set to 0, i.e. focusing on closely related individuals. An alternative is to use the full IBS based covariance matrix to obtain an estimate of the heritability explained by genotyped SNPs (), however, this requires removing related individuals [12]. If related individuals are included, the resulting estimate is neither an estimate of nor an estimate of .
Previous approaches to estimating the heritability explained by genotyped SNPs () required filtering related individuals, thereby increasing the standard error of the estimates. However, joint estimates of and can be obtained using two covariance matrices based on IBS>t and IBS. The first component provides an estimate of , and the second provides an estimate of . This approach removes the need to filter related individuals. Alternately, joint estimates of and can be obtained using two covariance matrices based on IBD and IBS, where here IBD replaces IBS>t to estimate .
Broad-sense heritability (H2) is the sum of additive, dominant, and epistatic components of heritability. The additive, dominant, environmental (ADE) model can be used to obtain joint estimates of dominance and additive components of heritability, using two covariance matrices based on IBD2 (two copies shared IBD) and IBD [22].
Below, we investigate all of these modeling approaches. Table S1 contains definitions of all parameters quantifying components of heritability that are used in the text.
Estimates of narrow-sense heritability (h2)
Ideally, estimates of narrow-sense heritability of a particular phenotype would be based on a genetic relationship matrix constructed from causal variants, representing the true genetic contribution to the phenotype [23]. However, as this set of variants is typically not known for most phenotypes, a proxy must be used for the pair-wise genetic covariance of individuals at the causal variants. Traditionally, this proxy has been derived from genealogical information, representing, for each pair of individuals in a sample, the expected fraction of their genomes that is identical-by-descent (IBD) – i.e. identical as a result of being inherited from a recent common ancestor [23]. The availability of dense genome-wide data from microarray SNP genotyping platforms has made it possible to directly estimate the fraction of the genome shared IBD between each pair of individuals (KIBD). However, fine-scale estimation of KIBD in population samples is dependent on information about the chromosomal phase of alleles, which requires long-range phasing of the data [17], [24], [25]. Previous studies reporting estimates in close relatives based on KIBD [26], [27], [28] had very high standard errors based on their study design and sample size. Recent work has examined IBD-based heritability estimates from distantly related individuals [29]. Ours is the first study to provide fine-scale IBD-based estimates of based on pairs of individuals at a range of relationship from siblings to distant relatives. We refer to these estimates as .
IBD-based estimates of for the 11 quantitative traits () are shown in Table 1. For these and subsequent estimates of h2, age, sex, and geographic region were included as covariates to prevent confounding. These estimates range from 0.099 for recombination rate to 0.691 for height. The only quantitative trait yielding an estimate not significantly different from 0 was sex-ratio of offspring. For each of the eight quantitative phenotypes with published estimates of , our estimates were smaller than the mean published estimate. For example, our estimate of 0.69 for height was lower than previous estimates of 0.80 [30], but was consistent with previous estimates in being lower for females (0.724 s.e. 0.019) than males (0.780 s.e. 0.029) [31].
Tab. 1. Narrow-sense heritability estimated from IBD () and thresholding IBS () for 11 quantitative traits. 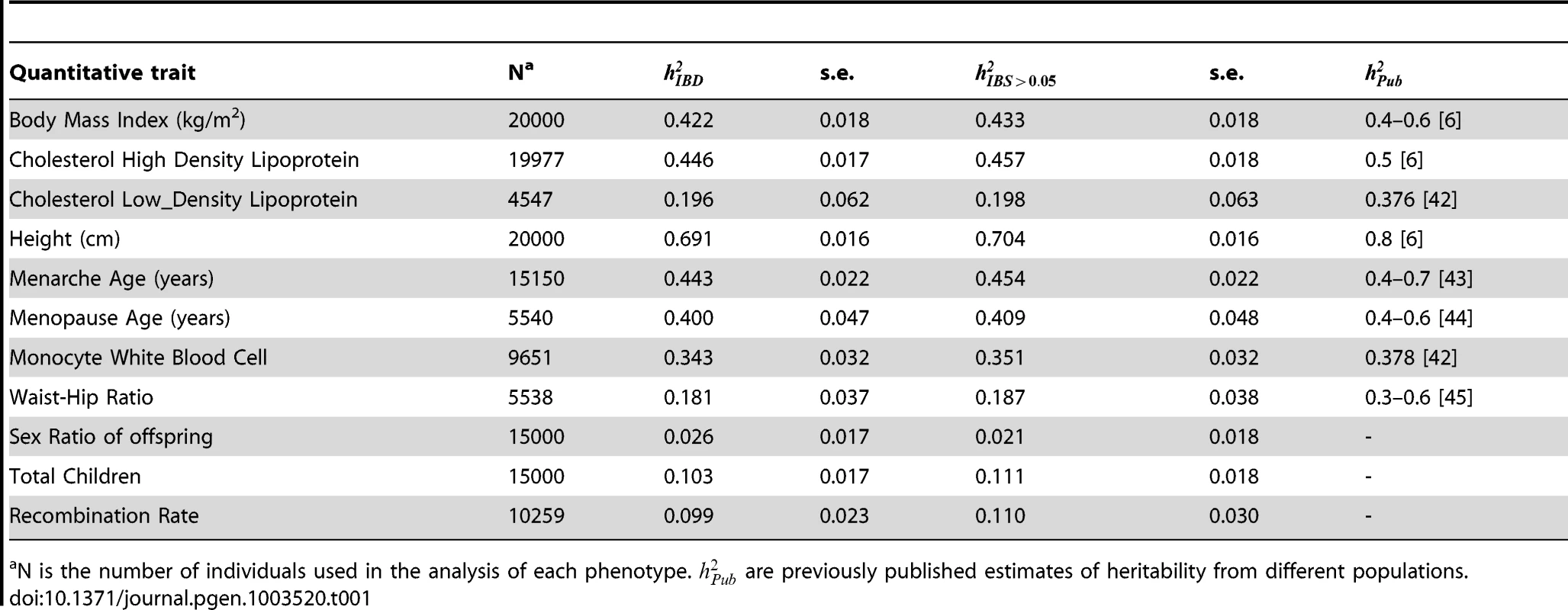
N is the number of individuals used in the analysis of each phenotype. are previously published estimates of heritability from different populations. Previous studies, based on either genealogical or direct estimates of IBD sharing, have been limited to closely related individuals (first-cousins or closer), and may therefore be upwardly biased due to the impact of shared environment, dominance, or epistatic interactions [10]. On average, our estimates of were lower than those from previous studies by a ratio of 0.75 (s.e. 0.067), most likely because the latter were inflated by one of the three aforementioned factors. We return to this point below, performing a pedigree-based analysis to assess the impact of these factors. Dichotomous phenotypes in this study were ascertained to increase the number of available cases, leading inflation in . A discussion of this inflation and the resulting estimates are presented in Text S1 and Table S2.
In most cases, researchers do not have access to long-range phased genotypes with which to estimate h2. One suggested solution to this problem is the use of KIBS, the genome-wide proportion of alleles shared identical-by-state (IBS) at all genotyped loci, as a substitute for KIBD [32], when estimating on the basis of closely-related pairs of individuals (it is assumed that KIBS provides a poor estimate of KIBD for distantly related pairs of individuals). Taking advantage of long-range phase based estimates of KIBD, we sought to evaluate the use of KIBS for the estimation of h2. For this purpose, we computed KIBS as defined in [12] and found that it produced downwardly biased estimates of for both simulated and real data sets that included many pairs of distantly related individuals (see Methods). As noted by Vattikuti et al [19], this bias is due to the fact that, when used to estimate h2, the KIBS matrix captures information from two distinct sources, depending on the degree of relationship between pairs of individuals. For large values of IBS it estimates genetic covariance over all SNPs in the genome. For low values of IBS it estimates genetic covariance over just those SNPs on the genotyping platform (see next section). Thus, the resulting heritability estimates from KIBS therefore tend to lie between the true value, , and the typically lower value of .
To avoid this bias, we implemented a different approach, retaining all individuals for the calculation of h2, but setting values of KIBS less than or equal to a threshold t (KIBS>t) to 0, for t = 0.00, 0.025 and 0.05. This threshold defines the separation between closely and distantly related individuals. We evaluated this approach using both simulations and real data sets and observed a significant downward bias of narrow-sense heritability estimated from tresholded IBS () at t = 0. For example, when t = 0 for height is 0.58, while when t = 0.05 = 0.70 (similar results were obtained for the other phenotypes). We observed no bias at t = 0.025 or t = 0.05 (see Methods and Table S3). To err on the side of caution, we present values for t = 0.05 () in Table 1 and Table S2, for the quantitative and dichotomous traits, respectively. The difference between narrow-sense heritability estimated from IBD ( ) and was less than 0.015 for all traits and not statistically significant for any of them. The correlation between the two estimators was 0.9998 and 0.9999 for the quantitative and dichotomous traits, respectively. Furthermore, in our extensive simulations over real data, the difference between the estimators was always less than 0.02 and not statistically significant (see Methods and Tables S3, S4, S5). These results indicate that when phase information is not available KIBS can provide unbiased and precise estimates of h2, by means of , in data consisting of a mixture of closely and distantly related pairs of individuals. The choice of threshold t is a function of the relatedness structure of the individuals in the study as well as the properties of the population they are drawn from (see Discussion).
Joint estimation of and for quantitative phenotypes
Recently, Yang et al [12] developed a method for estimating , the fraction of narrow sense heritability explained by genotyped SNPs (and SNPs in LD with genotyped SNPs). The interest in derives from the fact that it is the upper bound on the heritability that can be described from GWAS () conducted on the same genotyping platform used to estimate . The Yang et al. method is based on a variance component model with a genetic relationship matrix KIBS estimated from the genotyped SNPs. To prevent inflation, the method requires that all pairs of individuals have KIBS<0.025 [12]. In studies where the Yang et al. [12] approach has been applied [18], [19], the removal of related individuals resulted in a significant decrease in sample size and a concomitant increase in the standard error of the heritability estimates (e.g. a standard error of 19% in one study [18]). Filtering such that KIBS<0.025 for all individuals in our data leaves less than 3000 individuals, which is not adequate to estimate with low standard error(for example, resulting in a standard error for of 10.0% for height).
To enable unbiased calculation of in data sets that contain a both closely and distantly related pairs of individuals, we have devised an alternative approach based on a model with two variance components (see Methods). The first variance component, KIBS has a parameter and is an estimate of , the genetic variance due genotyped SNPs. The second variance component KIBS, has a parameter and is an estimate of , the total narrow-sense heritability (the subscript+is used for both parameters to denote that they are estimated simultaneously). Although we have access to fine-scale estimates of KIBD, based on long-range phased genotype data, we demonstrate the application of this approach using KIBS>t, because fine-scale KIBD estimates are typically not available to most researchers. We note that in the empirical results and in simulation, the use of KIBD and KIBS in the model produced results that were similar to those obtained using KIBS>t and KIBS (see Methods). Extensive testing of this model was performed to demonstrate that it estimates the appropriate quantities (see Methods), and estimates of closely match those of narrow-sense heritability estimated from tresholded IBS and IBD ( and ), both in our data and in simulations.
Table 2 shows heritability results for quantitative traits using the joint model where heritability estimated from thresholding IBS () and heritability explained by genotyped SNPs () are fit jointly. We examined the nine quantitative traits where h2>0. Our results are concordant with the previous estimates of for height, high-density lipoprotein (HDL), WHR, and BMI [6], [19]. For most of the traits, accounts for more than half of , with a maximum of 0.75 for waist-to-hip ratio (WHR), and a minimum of 0.33 for age at menopause. For each trait, we tested for deviation from a /h2 ratio of 0.53 (the average across all the traits) and found that only height, with a value of 0.58 was significantly different (p-value<0.0017, see Text S1). However, as our estimates of were smaller than previous estimates, the fraction 0.53 (s.e. 0.042) of variance explained by genotyped SNPs based on our estimates of heritability was larger than the fraction 0.40 (s.e. 0.037) based on published estimates [6].
Tab. 2. Heritability estimated from thresholding IBS () and heritability explained by genotyped SNPs (). 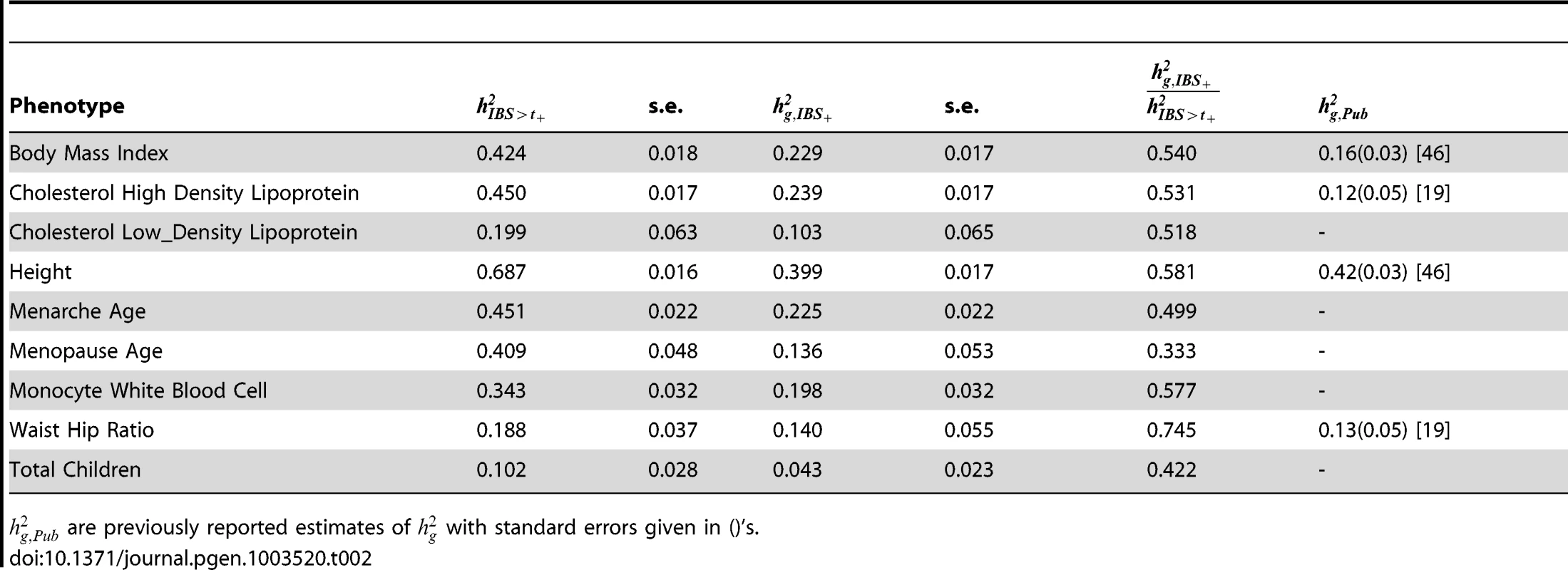
are previously reported estimates of with standard errors given in ()'s. Joint estimation of narrow-sense and heritability explained by genotyped SNPs for dichotomous phenotypes
For dichotomous phenotypes, ascertainment in samples with closely related pairs of individuals induces an upward bias in narrow-sense heritability jointly estimated from IBS above a threshold () when converting to the liability scale (Table S6 and Text S1). Thus, our estimates should be viewed as an upper bound. However, it is possible to account for case-control ascertainment amongst distantly related pairs when converting heritability explained by genotyped SNPs jointly estimated from IBS below a threshold () from the observed to the liability scale [33]. This correction is not possible when affected relatives are included in the study. For example, a study that ascertains affected sib pairs will have severely inflated heritability estimates, and the case-control ascertainment correction does not address this type of bias (see Text S1). Table 3 shows estimates on the liability scale, derived from a model with two variance components KIBS>t and KIBS, for 11 dichotomous traits. Estimates of primarily capture the heritability derived from distantly related pairs of individuals. Results on the observed scale are given in Table S7. The inflated narrow-sense heritability estimates of the dichotomous phenotypes leads to a lower ratio of heritability explained by genotyped SNPs () to .
Tab. 3. Narrow-sense heritability explained by genotyped SNPs () for dichotomous phenotypes on the liability scale. 
are previously reported estimates of with standard errors given in ()'s. Our results are lower than previous estimates of the heritability explained by genotyped SNPs () for rheumatoid arthritis (RA), 2 diabetes (T2D), and coronary artery disease (CAD) [34]. The differences between our estimates and previous estimates could be due to the use of population controls in our study rather than non-affected controls, differences in disease prevalence between populations, differences in the genotyping platform used, differences in ascertainment strategies such as age matching in previous work, or actual differences in the heritability of the phenotype across populations. If a small number of common variants were responsible for a large fraction of the phenotypic variation, they would have been identified by previous GWAS. However, since most of the loci identified through GWAS have a small effect, our results suggest a highly polygenic model of disease for the dichotomous phenotypes, as in the case of the quantitative traits. This is consistent with previous studies [6].
Estimation of heritability explained by shared environment, dominance, and epistasis
Shared environment, dominance effects and epistasis (i.e. non-additive interaction between variants) can upwardly bias estimates of in data sets that contain closely related pairs of individuals [10]. Phenotypic covariance in siblings can be strongly affected by dominance effects, and as siblings have correlated phenotypes due to shared environment, these two factors are strongly confounded [11]. In addition, Zuk et al [10] showed that epistatic interactions also lead to inflated estimates of and is an additional confounding factor. Inflation due to any of these factors affects interpretation of the relationship between and and is likely to result in overestimates of missing heritability when is estimated using closely related pairs of individuals. We adopted two approaches to test for evidence of inflation and to determine the extent to which it could be accounted for by shared environment, epistasis, or dominance effects (referred to collectively hereafter as dominance-like effects).
First, we estimated additive and dominance-like effects simultaneously under an ADE (additive, dominant, and environmental) model with variance components KIBD and KIBD2, where the latter represents the fraction of the genome with both chromosomes shared IBD for each pair of individuals [26]. A likelihood ratio test of the ADE model against the single variance component model of KIBD was performed (see Methods) [35], producing two heritability estimates the narrow sense heritability, and the heritability due to dominance-like effects (the subscript “”denotes that these two estimates are generated simultaneously from the same model). The sum of these two estimates is the broad sense heritability H2. The only class of relationship with significant IBD2 is siblings who share an expected ¼ of their genome IBD2. This analysis will therefore focus overwhelmingly on the difference between siblings and other classes of relationship. Siblings are also subject to epistatic interactions and shared environment and so this analysis will be influenced by all three factors (shared environment, dominance, and epistasis). We note that this analysis will not detect shared environment effects that decay exactly in proportion to genome-wide IBD.
We initially examined a subset of 11 quantitative and dichotomous traits, viewed as likely candidates for environmental effects, in a subset of 15,000 genotyped individuals using the ADE framework. The results for these phenotypes are shown in Table 4, with heritability estimates for dichotomous traits given on the observed scale. Six phenotypes exhibited that was significantly greater than zero, with an average value of 0.37, indicating the impact of dominance-like effects. Hypertension in pregnancy, T2D, CAD and osteoarthritis showed the strongest effects (see Figure S1). While these results give clear evidence of inflation of h2, they do not distinguish between the possible sources of inflation. The fact that the narrow sense heritability estimate decreases when fit jointly with demonstrates that the IBD based estimated conducted over relatives is susceptible to inflation.
Tab. 4. Joint estimates of heritability from two copy (dominant) IBD () and singly copy (additive) IBD (). 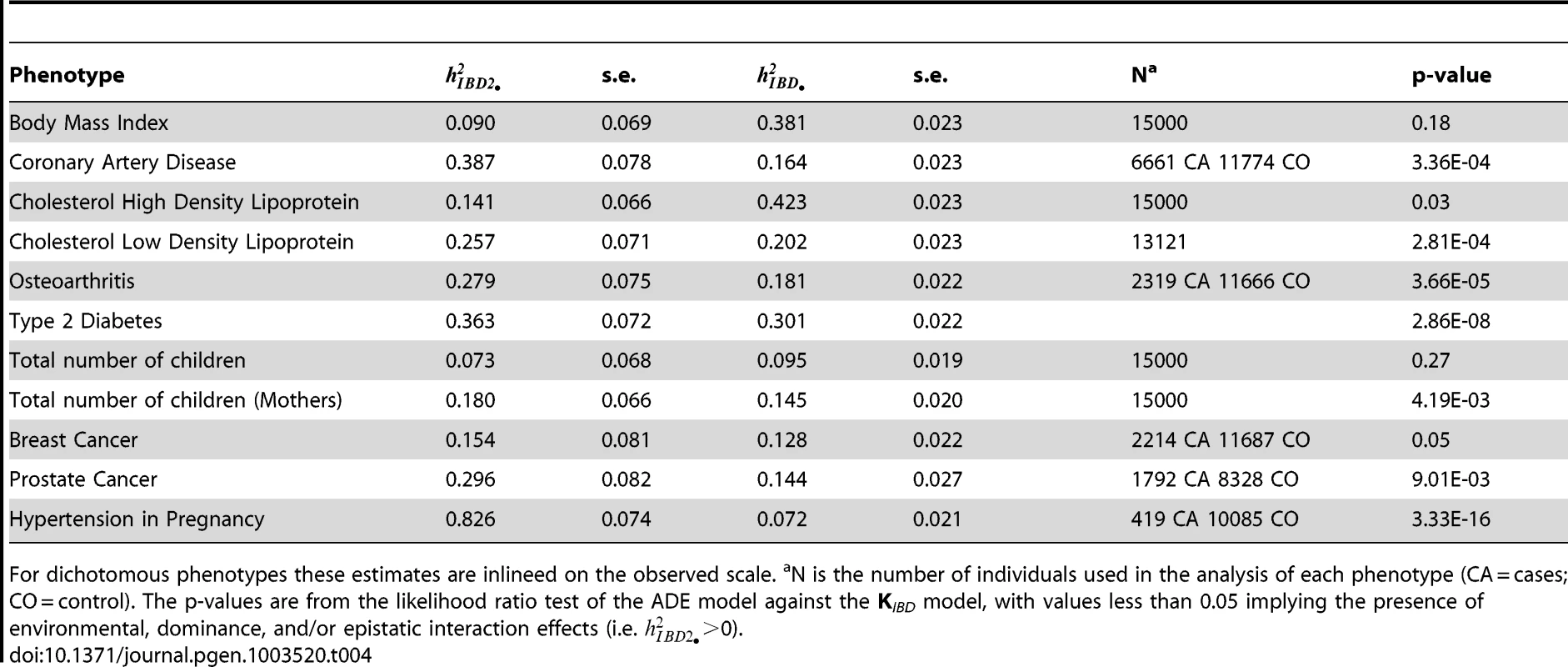
For dichotomous phenotypes these estimates are inlineed on the observed scale. aN is the number of individuals used in the analysis of each phenotype (CA = cases; CO = control). The p-values are from the likelihood ratio test of the ADE model against the KIBD model, with values less than 0.05 implying the presence of environmental, dominance, and/or epistatic interaction effects (i.e. >0). In order to address this issue, we performed a pedigree-based analysis, making use of genealogical information [36] to assess the effect of shared environment against those of dominance and epistasis. For each class of family relationship, we estimated for each phenotype by dividing the phenotypic correlation by the genealogical expectation for the fraction of genome shared IBD (see Methods). Errors in the genealogical database are believed to be small but may bias the estimates, especially for the more distant relatives [36]. Each source of inflation is expected to generate a distinct pattern of heritability estimates across the relationship classes. We extended our analyses to 17 of the original 23 phenotypes where, for each class of familial relationship, there were at least 100 pairs of individuals for continuous phenotypes and at least 50 cases and 50 controls for dichotomous phenotypes (the full set of phenotypes is given in Text S1). Figure 1 and Table S8 reveal a gradient of average estimates across the 17 phenotypes, ranging from 0.35 for sibs to 0.2 for avuncular pairs, that is inconsistent with dominance or epistasis being the sole source of , either individually or in combination. The large standard errors prevent more detailed conclusions about the relative contributions of environment and epistasis. It is possible that maternal and paternal half siblings have different environmental sharing, but due to their low numbers we analyzed them together.
Fig. 1. Average heritability estimates and 95% confidence intervals of 17 phenotypes for six classes of relationship. 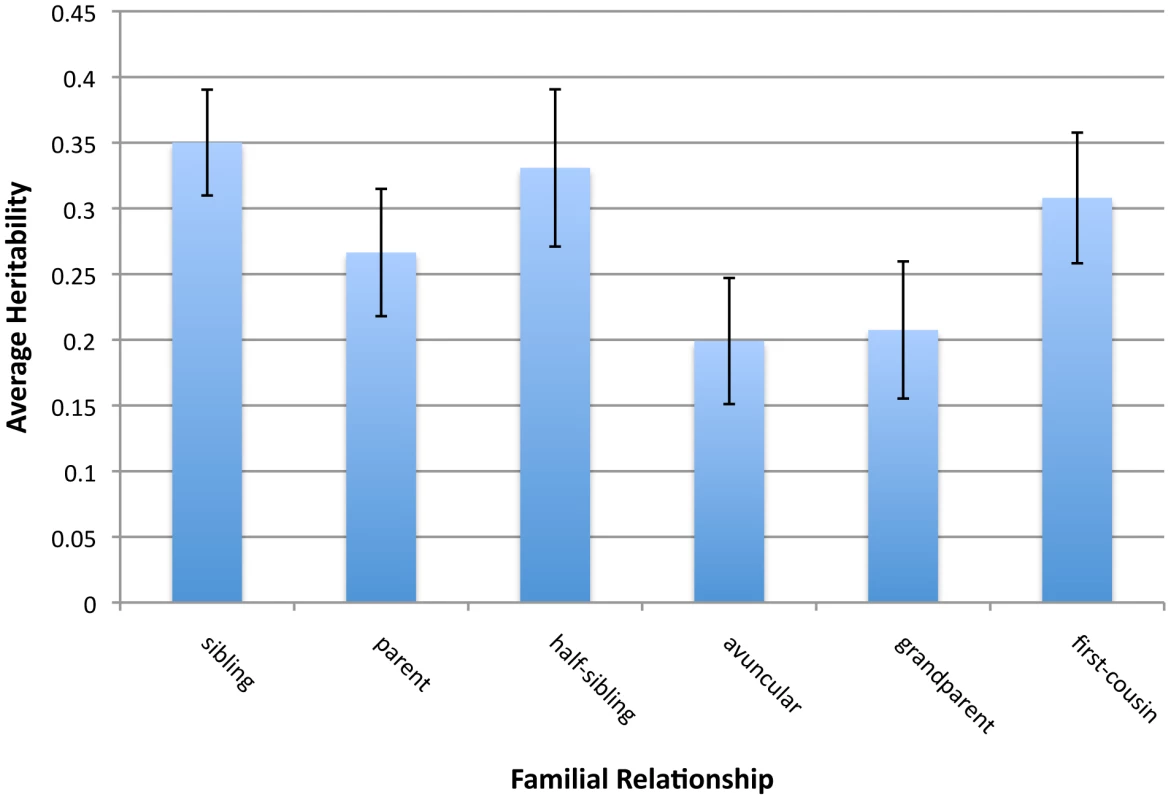
The differences in heritability estimate between classes of relationship are consistent with a shared-environment only effect on phenotypic correlation, but not with a dominance only or epistasis only effect on phenotypic correlation. If the heritability estimate of two copy IBD when fit jointly with IBD () were due to dominance, one would expect all classes of relationship to exhibit the same value of with the exception of siblings, but this is not what is observed. (Siblings are the only class with significant KIBD2 due to dominance and would have larger estimates of than any other class of relationship.) If were due to epistasis, one would expect a monotonic relationship between and KIBD [10], such that all classes sharing the same fraction of the genome IBD (such as half-siblings and grandparent-grandchild pairs) yield the same estimate of h2. Again, this is not what is observed. Finally, if were due to shared environment, one would expect that relationship classes that entail considerable shared environment through cohabitation (sibs, half-sibs and parent-offspring) would have greater values of than relationship classes with the same fraction of IBD but no cohabitation. Indeed, this is what is observed.
Our results show that estimates for half-siblings are greater than those of grandparent-grandchild pairs by 0.125 on average. This suggests that dominance or epistasis are not the sole sources of inflation in data sets containing many closely related pairs of individuals. Figure 1 does not imply that first cousins share more similar environments than parent and offspring or siblings. The first-cousin phenotypic correlation is multiplied by a factor of eight to estimate heritability, while the parent-offspring correlation is only multiplied by two. Thus, first-cousins could share substantially less similar environments (nearly four times less similar), and still have a higher estimate of heritability as a result.
Two additional results from Table S8 deserve further attention. First, the greater estimates obtained for parent-offspring than for avuncular pairs are consistent with shared environment. Second, the greater estimates obtained for first cousins than for grand-relatives and avuncular pairs (both have a twofold greater value of KIBD), suggests that first cousins have shared environmental factors stronger than either of these other classes of relationship. Although we condition on age a strong non-linear effect of age on phenotype, or a cohort effect, could produce this elevated correlation amongst first cousin phenotypes.
Discussion
We have made use of long-range phased genotype data and genealogical information from an Icelandic cohort to shed light on the problem of missing heritability, and the relative contributions of common and rare sequence variants and environmental factors to complex human phenotypes.
First, we examined IBD based estimation of narrow-sense heritability in data containing both closely and distantly related individuals. Our estimates were lower than previously published estimates, which were primarily based on closely related pairs of individuals. This suggests that previous estimates may be upwardly biased and that the fraction of variance described by known associations detected by GWAS of common variants is greater than previously thought. We also showed that estimates of based on thresholding IBS () were nearly identical to those based on IBD estimates derived from long-range phased genotype data. Thus, we demonstrate that it is possible to estimate using either IBD or IBS>t in cases where long-range phased genotypes are not available.
Second, we developed a new method to estimate (the heritability explained by genotyped SNPs), based on both closely and distantly related pairs of individuals, which has the additional advantage of providing a joint and directly comparable estimate of h2. The estimated value of is an upper bound on the amount of variation that can be described by SNPs on a given genotyping platform and is driven almost entirely by common variation. Previously, it was necessary to prune related individuals from data sets prior to calculation, substantially increasing the standard error around the estimate [19], [37]. In the case of height in our data set, the pruning approach resulted in a standard error for of 10%. In comparison, our method produced one of only 1.7%.
Finally, we investigated the impact of shared environment, dominance, and epistasis on estimates of in data sets that include pairs of closely related individuals. We found that estimates for several phenotypes, including type 2 diabetes and coronary artery disease, were significantly inflated due to such dominance-like effects. By examining patterns of correlation across multiple classes of relationship, we have demonstrated that the effects of shared environment outweigh those of epistasis and dominance. However, our results indicate that shared environment may be the major contributor to inflated values of obtained with data sets that include closely related pairs of individuals. They also suggest that this inflation, as opposed to consistently lower heritabilities in Iceland, is the major source of difference between our estimates those of previously studied populations. MZ/DZ twin estimates of assume that the two classes of siblings share the same relevant environmental exposures. If this is true, then inflation from such studies may be due instead to epistasis.
A standard way to quantify the contribution of environmental effects is to fit an ACE model [13]. However, a complexity with this approach is that it is unclear which relative classes should be modeled as sharing a common environment. For example, do parent/child pairs have the same environmental sharing as siblings? We believe this merits further investigation, although it is outside the scope of our current work.
Interestingly, our estimate of the heritability of height (0.69) is lower than previous estimates (0.8) [30] based on studies of twins, siblings, parent-offspring, half-siblings, and first-cousins. Visscher [26], [27] previously used estimates of IBD amongst siblings instead of the expected value of 0.5 to estimate the heritability of height. The standard error of his estimate (mean 0.8, standard error 0.1) was too large for this estimate to be statistically different from either 0.69 or 0.8. We note that this estimate would be inflated in the presence of epistasis since the study focuses on siblings. Zuk et al [10] proposed that heritability estimates of closely related individuals maybe inflated in the presence of epistasis, but an epistasis-only explanation would require a deflation in estimates moving from closely related individuals (siblings) to more distant relationships (first-cousins), which is not observed. One possible explanation is inflation in previous estimates of height due to a combination of epitasis and shared environment across multiple levels of relationship (e.g. siblings to first-cousins). These sources of inflation would be reduced when more distantly related individuals are available as is uniquely the case in this study (see Text S1). Heritability may vary between segments of the population, such as males and females. In this work we chose not to subdivide the population into segments, but instead make our estimates in the entire population. The covariates we used (age, sex, geographic region) will account for mean differences but not differences in variance or heritability between these groups.
We conclude that, for quantitative traits, more than half of is explained by genotyped SNPs. Because of our smaller estimates of h2, this fraction is larger than previous estimates [6], [19], [34]. It is encouraging to learn that more can be discovered using the common variants on microarray SNP genotyping platforms used in GWAS than some recent pessimistic reports have concluded [38], [39]. One potential reason for the differences between and is that rare variation accounts for a significant fraction of the total narrow-sense heritability. If this is the case, then genome-wide sequencing studies offer a potential route to capturing the remaining heritability.
Methods
Ethics statement
This research was approved by the Data Protection Commission of Iceland and the National Bioethics Committee of Iceland. The appropriate informed consent was obtained for all sample donors.
deCODE data set
We analyzed 38,167 individuals from the deCODE data set genotyped on the Illumina 300K chip. Owing to the sensitive nature of genotype data, access to these data can only be granted at the headquarters of deCODE Genetics in Iceland. The details of the genotyping, quality control, IBD estimation and genealogy are described elsewhere [20], [28]. . The 11 quantitative phenotypes examined in this study are body mass index (BMI), high density lipoprotein cholesterol (HDL), low density lipoprotein cholesterol (LDL), height, age at menarche, age at menopause, monocyte white blood cell count, waist hip ratio (WHR), sex ratio, number of offspring, and recombination rate (see Table 1). The 11 dichotomous phenotypes are alcohol dependence, asthma, autoimmune Systemic RA+SLE+SSc+AS (rheumatoid arthritis, systemic lupus erythematosus, systemic sclerosis, ankylosing spondylitis), T-cell mediated autoimmune disease, breast cancer (BC), coronary artery disease (CAD), hypertension in pregnancy, osteoarthritis, prostate cancer (PC), rheumatoid arthritis (CCP positive and negative) (RA), type 2 diabetes (T2D), and left handedness (see Table S2). Dichotomous phenotypes are diagnosed by physicians with the exception of left-handedness, which is measured by self-report. Continuous phenotypes are measured by health professionals, medical laboratories, and an extended genealogy [36]. The exceptions are age at menopause and menarche, which are measured by self-report.
The deCODE Genetics genealogy database, containing all contemporary Icelanders and most of their ancestors going back to the year 1650, was used to determine the genealogical relationships between individuals [36].
A description of the phenotypes is given in Text S1. Estimation of IBD2 is analogous to estimation of IBD, but only includes instances where individuals are IBD on both chromosomes.
Statistical methods
We used a linear mixed model approach to estimate the components of heritability in our data sets. In this approach, each phenotype Y is modeled from a multivariate normal distribution where is the mean phenotype. Each of the components of heritability described correspond to a different model for the phenotypic covariance matrix .
For a normalized phenotype with mean 0 and variance 1, to estimate , we set and find the estimate of that maximized the restricted maximum likelihood (REML) of Y being generated from using the GCTA software [40]. We applied the same method to estimate and using the kinship matrices KIBS>t and KIBS respectively. To jointly estimate + we fit Y with . We applied the same method to estimate + using kinship matrices KIBD and KIBS. The intuition for this approach is that the large elements of genetic covariance matrix KIBS are good estimates of the pair-wise IBD of individuals. Indeed, this is why is a good estimate of . However, the small elements of KIBS only provide information about SNPs in LD with those on the genotyping platform. This is why the KIBS applied to unrelated individuals in the approach of Yang et al. estimates . By breaking KIBS into two components, one provides estimates of the phenotypic variance explained by SNPs on the genotyping platform, and the other provides an estimate of the remaining phenotypic variance. The total narrow-sense heritability is the sum of the parameters for KIBS>t and KIBS, and the heritability explained by genotyped SNPs is the parameter for KIBS.
To estimate and we fit Y with . The parameter for KIBD2 is a combination of shared environment, dominance, and epistatic effects. The parameter for KIBD is the narrow-sense heritability. Under the assumption of no shared environment or epistatic effects, the sum of these estimates is the broad-sense heritability. In all cases we adjusted for age, gender, and region of Iceland as fixed effects. We use REML including a constant vector instead of ML to prevent bias in heritability estimation [35]. We estimated the prevalence of each dichotomous phenotype as the fraction of cases in the entire cohort.
The KIBS matrix is estimated as defined in [12]. Entry j,k is
where xij is the genotype (0,1,2), N is the number of SNPs, and pi is the minor allele frequency of SNP i in the study. Entry j,j is an estimate of the inbreeding coefficient . KIBS>t is the KIBS matrix with all entries less than t set to zero, with the exception of the diagonal, which is not changed.Entry (i,j) of the KIBD matrix is the fraction of the genome shared IBD between individuals i and j. Pair-wise IBD estimates were estimated as described in [28]
where L is the length of the genome and IBD [j,k]at nucleotide s is 1 if individuals j,k are IBD at position s and 0 otherwise. Entry (j,j) is 1+ the fraction of the genome shared IBD between the maternal and paternal copies. The IBS matrices are all adjusted to have mean zero (Equation 1) and the IBD matrices are not (Equation 2). Entry (i,j) of the KIBD2 matrix is defined similarly, but pair-wise IBD2 estimates (both chromosomes IBD) are used in place of pair-wise IBD estimates. That is, a pair of individuals is IBD2 at a particular SNP if they are IBD on both haplotypes. Entry, (j,j) is set to 1.0. We note that none of the kinship matrices defined here, and hence none of the resulting heritability estimates rely on the genealogy, but are based on direct estimates from the genetic data.Simulations with simulated genotypes
We performed a set of experiments over simulated genotype data in order verify that our estimates of and our estimates of were estimating the correct heritabilities. We generated simulated observed genotypes of individuals as random draws from a binomial distribution with minor allele frequencies p1,p2,…,pN where the number of SNPs N = 5,000 and pi drawn uniformly between 0.05 and 0.5. We then repeated this process to create unobserved genotypes for each individual. The observed genotypes represent those on a genotyping platform and the unobserved represent those not in LD with the genotyped SNPs.
To simulate a pair individuals with x% of their genome shared IBD, we copied x% of the SNPs of the first individual's haplotypes onto the corresponding SNPs of the second individual in the pair. We normalized the genotypes to have mean 0 and variance 1 and set the effect size for each SNP to be the square root of 0.5/10000. The phenotype for each individual is the sum over all SNPs of the product of the normalized genotype and the effect size plus noise drawn from a random distribution with mean 0 and variance 0.5. This gives a phenotype with mean 0, variance 1, a of heritability 50%, of which 50% is due to observed genotypes and 50% is due to unobserved genotypes.
We then constructed relationship matrices K using the observed genotypes. For KIBD, we assumed that we had access to the true value of IBD for each pair of individuals. We constructed data sets of 1,400 individuals with several different types of relationship structure, created 1,000 replicates of each data set, and estimated narrow-sense heritability using the IBD matrix KIBD, using the IBS matrix KIBS>t, and using the complete IBS matrix KIBS. We estimated the joint estimates of and using the approximation for IBD, and compared this to the joint estimates , which use IBD directly.
The results shown in Table S3 demonstrate that KIBD and KIBS>t give good estimates of when there are closely related individuals in the data set, but have a high variance when the relationships are more distant. KIBS is not a good estimator of either or when there are related individuals in the data set, since it lies in between and . Both KIBD+KIBS and KIBS>t+KIBS provide joint estimates of + without the need to remove related individuals. When one of every pair of individuals with KIBS>0.025 is removed from the data set, the estimate of has the same mean as when estimated simultaneously with KIBS>t, but the variance is significantly higher.
When the related individuals are closely related (e.g. K = 0.5), KIBS>t is a good estimator of KIBD and the mean heritability estimate is the true . However, while pair-wise IBS is a good estimate of the pair-wise IBD, the variance of the IBS estimate is distributed according to the observed genotypes. The heritability estimate from KIBS is therefore biased towards the heritability explained by genotyped SNPs. This is why always lies in between and and using KIBS to estimate narrow-sense heritability without thresholding can lead to biased heritability estimates.
When the relatedness of individuals in the data set is moderate (e.g. K = 0.125), the joint model KIBS>t+KIBS does not provide a good estimate of since KIBS>t will be influenced by genotyped variants. However, is still unbiased and the variance of is lower than it would have been if related individuals were removed. Therefore, we have a means of including distantly related individuals when estimating . The value of KIBS>t as an estimate for the true heritability depends on the relatedness structure of the data set. In data sets with families, such as the cohort examined here, or the FHS data set [19], it is possible to estimate both and . In data sets with moderate relatedness, the robustness of the thresholding approach should be examined via simulation.
Simulations with real genotypes
We performed a similar set of experiments to those described above, but this time used real genotype data with simulated phenotypes in order to verify that issues due to LD, IBD estimation, population structure, or other similar confounders did not affect our results. We selected 8000 individuals randomly from the complete data set and generated two sub-phenotypes for each individual. We generated two sets of causal variants C1 and C2 by selecting a causal variant every 500 SNPs along the even chromosomes for C1 and repeating the process along the odd chromosomes for C2. We chose effect sizes α1 and α2 for C1 and C2 respectively and set the sub-phenotypes for an individual by summing the product of their genotypes (0,1,2) times the corresponding effect sizes. We then added random noise ε1 and ε2 to each sub-phenotype and summed together the two sub-phenotypes to generate a final phenotype for each individual. The even chromosomes correspond to the observed genotypes in a GWAS and the odd chromosomes correspond to SNPs not in LD with the genotyped SNPs. For any choice of α1 and α2, and variances of ε1 and ε2 we can compute the heritability of the phenotype due to all SNPs and the heritability explained by genotyped SNPs .
We recomputed the relationship matrices K using only the even chromosomes. For each simulated phenotype we estimated heritability using KIBD, KIBS, KIBS>t, and KIBS>t+KIBS. The results are shown in Tables S5, S7 and as was the case for the simulated synthetic data sets above, the heritability estimates are within one standard deviation of the true value in all cases with the exception of KIBS, which always lies between and . We confirm the bias of using KIBS by examining the estimate of in several real phenotypes (Table S9). We observe that it always lies between and .
Heritability estimation of classes of related individuals
For a given class of relatives, (e.g. siblings), for each phenotype we computed the correlation between the phenotype across all pairs of that class. The heritability estimate was then generated by dividing the correlation by the fraction of the genome expected to be shared IBD (e.g. 0.5 for siblings). It is not possible to place standard errors on the heritability estimate of the phenotypes due to the complex relatedness structure of the individuals in each class. One pair of siblings for example, might be the grandfather and granduncle of another pair of siblings. However, it is possible to compute an empirical mean and standard deviation across traits.
To compare the classes of relatives we computed the empirical mean and standard deviation of the differences of the heritability estimates across traits. The standard error of the difference is the standard deviation estimate divided by the square root of the number of phenotypes (17 in this case). We applied a Wald test to determine the p-value [41].
To determine the significance of the combined effects of shared environment, dominance, and epistatic interaction we constructed a one degree of freedom likelihood ratio test. We computed the likelihood of the ADE model fit with covariance matrices KIBD2+KIBD and the likelihood of the narrow-sense heritability estimated from KIBD.
Upward biases in narrow-sense heritability estimates
The heritability estimates in Table 1 and Table S2 may be upwardly biased due to shared environment since closely related individuals will have correlated phenotyped due to shared genetics as well as shared environment. The heritability estimates on the liability scale in Table S2 may be additionally upwardly biased due to sample ascertainment. As affected individuals in this analysis were non-randomly ascertained with respect to disease status and family relationship (for example, the probability of ascertaining two affected sibs is greater than that of ascertaining two affected first-cousins.), all estimates based on related pairs of individuals will tend to be inflated. We converted heritability estimates from the observed to liability scale (see Table S3) using the prevalences shown in Table S2 [33], noting that these estimates represent an upper bound. To our knowledge, no method exists to adjust estimates for this type of ascertainment.
Supporting Information
Zdroje
1. HindorffLA, SethupathyP, JunkinsHA, RamosEM, MehtaJP, et al. (2009) Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc Natl Acad Sci U S A 106 : 9362–9367.
2. MaherB (2008) Personal genomes: The case of the missing heritability. Nature 456 : 18–21.
3. EichlerEE, FlintJ, GibsonG, KongA, LealSM, et al. (2010) Missing heritability and strategies for finding the underlying causes of complex disease. Nat Rev Genet 11 : 446–450.
4. ManolioTA, CollinsFS, CoxNJ, GoldsteinDB, HindorffLA, et al. (2009) Finding the missing heritability of complex diseases. Nature 461 : 747–753.
5. GibsonG (2011) Rare and common variants: twenty arguments. Nat Rev Genet 13 : 135–145.
6. VisscherPM, BrownMA, McCarthyMI, YangJ (2012) Five Years of GWAS Discovery. Am J Hum Genet 90 : 7–24.
7. DicksonSP, WangK, KrantzI, HakonarsonH, GoldsteinDB (2010) Rare variants create synthetic genome-wide associations. PLoS Biol 8: e1000294 doi:10.1371/journal.pbio.1000294
8. HillWG, GoddardME, VisscherPM (2008) Data and theory point to mainly additive genetic variance for complex traits. PLoS Genet 4: e1000008 doi:10.1371/journal.pgen.1000008
9. WrayNR, PurcellSM, VisscherPM (2011) Synthetic associations created by rare variants do not explain most GWAS results. PLoS Biol 9: e1000579 doi:10.1371/journal.pbio.1000579
10. ZukO, HechterE, SunyaevSR, LanderES (2012) The mystery of missing heritability: Genetic interactions create phantom heritability. Proc Natl Acad Sci U S A
11. VisscherPM, HillWG, WrayNR (2008) Heritability in the genomics era–concepts and misconceptions. Nat Rev Genet 9 : 255–266.
12. YangJ, BenyaminB, McEvoyBP, GordonS, HendersAK, et al. (2010) Common SNPs explain a large proportion of the heritability for human height. Nat Genet 42 : 565–569.
13. Falconer DS (1986) Introduction to quantitative genetics. Burnt Mill, Harlow, Essex, England New York: Longman Scientific & Technical ; Wiley. viii, 340 p. p.
14. Lango Allen H, Lettre G, Estrada K, Berndt MN, Weedon MN, Abecasis GR, Boehnke M, Gieger C, Gudbjartsson D, Heard-Costa NL, Jackson AU, McCarthy MI, Rivadeneira F, Smith A, Soranzo N, Uitterlinden AG, Frayling TM, Hirschhorn JN, GIANT Consortium. The identification of over 135 loci involved in adult height variation provides important insights into the contribution of common variation to a model complex trait. Talk presented at the 59th annual meeting of the American Society of Human Genetics, October 22, 2009, Honolulu, HI.
15. PasaniucB, ZaitlenN, LettreG, ChenGK, TandonA, et al. (2011) Enhanced statistical tests for GWAS in admixed populations: assessment using African Americans from CARe and a Breast Cancer Consortium. PLoS Genet 7: e1001371 doi:10.1371/journal.pgen.1001371
16. SoHC, LiM, ShamPC (2011) Uncovering the total heritability explained by all true susceptibility variants in a genome-wide association study. Genet Epidemiol 35 : 447–456.
17. KangHM, SulJH, ServiceSK, ZaitlenNA, KongSY, et al. (2010) Variance component model to account for sample structure in genome-wide association studies. Nat Genet 42 : 348–354.
18. DearyIJ, YangJ, DaviesG, HarrisSE, TenesaA, et al. (2012) Genetic contributions to stability and change in intelligence from childhood to old age. Nature 482 : 212–215.
19. VattikutiS, GuoJ, ChowCC (2012) Heritability and Genetic Correlations Explained by Common SNPs for Metabolic Syndrome Traits. PLoS Genet 8: e1002637 doi:10.1371/journal.pgen.1002637
20. KongA, MassonG, FriggeML, GylfasonA, ZusmanovichP, et al. (2008) Detection of sharing by descent, long-range phasing and haplotype imputation. Nat Genet 40 : 1068–1075.
21. KendlerKS, NealeMC, KesslerRC, HeathAC, EavesLJ (1993) A test of the equal-environment assumption in twin studies of psychiatric illness. Behav Genet 23 : 21–27.
22. Falconer DS (1989) Introduction to quantitative genetics. Burnt Mill, Harlow, Essex, England New York: Longman Wiley. xii, 438 p. p.
23. PowellJE, VisscherPM, GoddardME (2010) Reconciling the analysis of IBD and IBS in complex trait studies. Nat Rev Genet
24. BrowningSR, BrowningBL (2010) High-resolution detection of identity by descent in unrelated individuals. Am J Hum Genet 86 : 526–539.
25. GusevA, LoweJK, StoffelM, DalyMJ, AltshulerD, et al. (2009) Whole population, genome-wide mapping of hidden relatedness. Genome Res 19 : 318–326.
26. VisscherPM, MedlandSE, FerreiraMA, MorleyKI, ZhuG, et al. (2006) Assumption-free estimation of heritability from genome-wide identity-by-descent sharing between full siblings. PLoS Genet 2: e41 doi:10.1371/journal.pgen.0020041
27. VisscherPM, MacgregorS, BenyaminB, ZhuG, GordonS, et al. (2007) Genome partitioning of genetic variation for height from 11,214 sibling pairs. Am J Hum Genet 81 : 1104–1110.
28. PriceAL, HelgasonA, ThorleifssonG, McCarrollSA, KongA, et al. (2011) Single-tissue and cross-tissue heritability of gene expression via identity-by-descent in related or unrelated individuals. PLoS Genet 7: e1001317 doi:10.1371/journal.pgen.1001317
29. BrowningSR, BrowningBL (2013) Identity-by-descent-based heritability analysis in the Northern Finland Birth Cohort. Hum Genet 132 : 129–138.
30. VisscherPM, McEvoyB, YangJ (2010) From Galton to GWAS: quantitative genetics of human height. Genet Res (Camb) 92 : 371–379.
31. SilventoinenK, SammalistoS, PerolaM, BoomsmaDI, CornesBK, et al. (2003) Heritability of adult body height: a comparative study of twin cohorts in eight countries. Twin Res 6 : 399–408.
32. HayesBJ, VisscherPM, GoddardME (2009) Increased accuracy of artificial selection by using the realized relationship matrix. Genet Res (Camb) 91 : 47–60.
33. LeeSH, WrayNR, GoddardME, VisscherPM (2011) Estimating Missing Heritability for Disease from Genome-wide Association Studies. Am J Hum Genet 88 : 294–305.
34. StahlEA, WegmannD, TrynkaG, Gutierrez-AchuryJ, DoR, et al. (2012) Bayesian inference analyses of the polygenic architecture of rheumatoid arthritis. Nat Genet
35. Lynch M, Walsh B (1998) Genetics and analysis of quantitative traits. Sunderland, Mass.: Sinauer. xvi, 980 p. p.
36. HelgasonA, PalssonS, GudbjartssonDF, KristjanssonT, StefanssonK (2008) An association between the kinship and fertility of human couples. Science 319 : 813–816.
37. DearyIJ, YangJ, DaviesG, HarrisSE, TenesaA, et al. (2012) Genetic contributions to stability and change in intelligence from childhood to old age. Nature
38. GoldsteinDB (2009) Common genetic variation and human traits. N Engl J Med 360 : 1696–1698.
39. McClellanJ, KingMC (2010) Genetic heterogeneity in human disease. Cell 141 : 210–217.
40. YangJ, LeeSH, GoddardME, VisscherPM (2011) GCTA: A Tool for Genome-wide Complex Trait Analysis. Am J Hum Genet 88 : 76–82.
41. Wasserman L (2005) All of Statistics: Springer.
42. PiliaG, ChenWM, ScuteriA, OrruM, AlbaiG, et al. (2006) Heritability of cardiovascular and personality traits in 6,148 Sardinians. PLoS Genet 2: e132 doi:10.1371/journal.pgen.0020132
43. TowneB, CzerwinskiSA, DemerathEW, BlangeroJ, RocheAF, et al. (2005) Heritability of age at menarche in girls from the Fels Longitudinal Study. Am J Phys Anthropol 128 : 210–219.
44. MurabitoJM, YangQ, FoxC, WilsonPW, CupplesLA (2005) Heritability of age at natural menopause in the Framingham Heart Study. J Clin Endocrinol Metab 90 : 3427–3430.
45. FeitosaMF, BoreckiI, HuntSC, ArnettDK, RaoDC, et al. (2000) Inheritance of the waist-to-hip ratio in the National Heart, Lung, and Blood Institute Family Heart Study. Obes Res 8 : 294–301.
46. YangJ, ManolioTA, PasqualeLR, BoerwinkleE, CaporasoN, et al. (2011) Genome partitioning of genetic variation for complex traits using common SNPs. Nat Genet 43 : 519–525.
Štítky
Genetika Reprodukční medicína
Článek Attachment Site Selection and Identity in Bxb1 Serine Integrase-Mediated Site-Specific RecombinationČlánek Bck2 Acts through the MADS Box Protein Mcm1 to Activate Cell-Cycle-Regulated Genes in Budding YeastČlánek High-Resolution Transcriptome Maps Reveal Strain-Specific Regulatory Features of Multiple IsolatesČlánek Neuropeptides Function in a Homeostatic Manner to Modulate Excitation-Inhibition Imbalance inČlánek Implicates Tyrosine-Sulfated Peptide Signaling in Susceptibility and Resistance to Root Infection
Článek vyšel v časopisePLOS Genetics
Nejčtenější tento týden
2013 Číslo 5- IVF a rakovina prsu – zvyšují hormony riziko vzniku rakoviny?
- Transthyretinová amyloidóza z pohledu neurologa a kardiologa aneb jak se vyhnout „misdiagnostice“?
- Akutní intermitentní porfyrie
- Souvislost haplotypu M2 genu pro annexin A5 s opakovanými reprodukčními ztrátami
- Prof. Petr Urbánek: Potřebujeme najít pacienty s nediagnostikovanou akutní intermitentní porfyrií
-
Všechny články tohoto čísla
- Functional Elements Are Embedded in Structurally Constrained Sequences
- RNA–Mediated Epigenetic Heredity Requires the Cytosine Methyltransferase Dnmt2
- Loss of Expression and Promoter Methylation of SLIT2 Are Associated with Sessile Serrated Adenoma Formation
- Attachment Site Selection and Identity in Bxb1 Serine Integrase-Mediated Site-Specific Recombination
- Human Genetics in Rheumatoid Arthritis Guides a High-Throughput Drug Screen of the CD40 Signaling Pathway
- Genome-Wide Analysis in German Shepherd Dogs Reveals Association of a Locus on CFA 27 with Atopic Dermatitis
- Liver X Receptors Protect from Development of Prostatic Intra-Epithelial Neoplasia in Mice
- Chromosomal Organization and Segregation in
- A Statistical Framework for Joint eQTL Analysis in Multiple Tissues
- Cell Polarity and Patterning by PIN Trafficking through Early Endosomal Compartments in
- Bck2 Acts through the MADS Box Protein Mcm1 to Activate Cell-Cycle-Regulated Genes in Budding Yeast
- High-Resolution Transcriptome Maps Reveal Strain-Specific Regulatory Features of Multiple Isolates
- Neuropeptides Function in a Homeostatic Manner to Modulate Excitation-Inhibition Imbalance in
- A Compendium of Nucleosome and Transcript Profiles Reveals Determinants of Chromatin Architecture and Transcription
- Wnt Signaling Regulates the Lineage Differentiation Potential of Mouse Embryonic Stem Cells through Tcf3 Down-Regulation
- Filamin and Phospholipase C-ε Are Required for Calcium Signaling in the Spermatheca
- The Specificity and Flexibility of L1 Reverse Transcription Priming at Imperfect T-Tracts
- Imputation-Based Meta-Analysis of Severe Malaria in Three African Populations
- Implicates Tyrosine-Sulfated Peptide Signaling in Susceptibility and Resistance to Root Infection
- Clathrin and AP2 Are Required for Phagocytic Receptor-Mediated Apoptotic Cell Clearance in
- Encodes CDF Transporters That Excrete Zinc from Intestinal Cells of and Act in a Parallel Negative Feedback Circuit That Promotes Homeostasis
- Global Properties and Functional Complexity of Human Gene Regulatory Variation
- DNA Binding of the Cell Cycle Transcriptional Regulator GcrA Depends on N6-Adenosine Methylation in and Other
- Side Effects: Substantial Non-Neutral Evolution Flanking Regulatory Sites
- From Paramutation to Paradigm
- From Mouse to Human: Evolutionary Genomics Analysis of Human Orthologs of Essential Genes
- Distinct Translational Control in CD4 T Cell Subsets
- Female Bias in and Regulation by the Histone Demethylase KDM6A
- ATM–Dependent MiR-335 Targets CtIP and Modulates the DNA Damage Response
- HDAC7 Is a Repressor of Myeloid Genes Whose Downregulation Is Required for Transdifferentiation of Pre-B Cells into Macrophages
- The Majority of Primate-Specific Regulatory Sequences Are Derived from Transposable Elements
- Identification of Meiotic Cyclins Reveals Functional Diversification among Plant Cyclin Genes
- EGL-13/SoxD Specifies Distinct O and CO Sensory Neuron Fates in
- Congruence of Additive and Non-Additive Effects on Gene Expression Estimated from Pedigree and SNP Data
- Using Extended Genealogy to Estimate Components of Heritability for 23 Quantitative and Dichotomous Traits
- Ikbkap/Elp1 Deficiency Causes Male Infertility by Disrupting Meiotic Progression
- Analysis of the Genetic Basis of Disease in the Context of Worldwide Human Relationships and Migration
- Duplication and Retention Biases of Essential and Non-Essential Genes Revealed by Systematic Knockdown Analyses
- Strong Purifying Selection at Synonymous Sites in
- , a Susceptibility Gene for Type 1 and Type 2 Diabetes, Modulates Pancreatic Beta Cell Apoptosis via Regulation of a Splice Variant of the BH3-Only Protein
- Chromosome Movements Promoted by the Mitochondrial Protein SPD-3 Are Required for Homology Search during Meiosis
- The Secretory Pathway Calcium ATPase PMR-1/SPCA1 Has Essential Roles in Cell Migration during Embryonic Development
- The Genomic Signature of Crop-Wild Introgression in Maize
- CDK4 T172 Phosphorylation Is Central in a CDK7-Dependent Bidirectional CDK4/CDK2 Interplay Mediated by p21 Phosphorylation at the Restriction Point
- Genome-Wide Identification of Regulatory RNAs in the Human Pathogen
- PLOS Genetics
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Using Extended Genealogy to Estimate Components of Heritability for 23 Quantitative and Dichotomous Traits
- HDAC7 Is a Repressor of Myeloid Genes Whose Downregulation Is Required for Transdifferentiation of Pre-B Cells into Macrophages
- Female Bias in and Regulation by the Histone Demethylase KDM6A
- ATM–Dependent MiR-335 Targets CtIP and Modulates the DNA Damage Response
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání





