-
Články
- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Statistika v biomedicínském výzkumu II
Statistics in biomedical research II
The article focuses on data processing and data analysis. It briefly describes basic descriptive statistics – measures of central tendency and variability for continuous data. Particular attention is paid to the correct choice of descriptive statistics of central tendency (arithmetic mean, median, modus) and variability (standard deviation and quantiles) regarding data distribution. It explains basic types of data distribution – symmetric, right skewed and left skewed. Attention is paid to the normal Gaussian distribution and its statistical properties. There are various types of distribution for continuous biomedical variables.
It describes the basic steps of hypothesis testing as a method of inductive statistics. It explains the difference between parametric and non-parametric statistical tests. Parametric methods are based on normal distribution and use mean and standard deviation. Non-parametric methods are based on rank. There is an overview of various kinds of parametric and non-parametric tests for hypothesis testing of continuous variables. The importance of choosing the correct parametric or a non-parametric method is emphasized.KEYWORDS:
descriptive statistics – mean – standard deviation – quantile – normal Gaussian distribution – parametric and non-parametric tests
Autoři: K. Langová
; J. Zapletalová; L. Ličman
Působiště autorů: Ústav lékařské biofyziky, Lékařská fakulta UP v Olomouci
Vyšlo v časopise: Anest. intenziv. Med., 28, 2017, č. 3, s. 183-187
Kategorie: Speciální článek
Souhrn
Článek se zabývá zpracováním a analýzou dat. Stručně jsou popsány základní popisné statistiky polohy a variability spojitých dat. Pozornost je věnována správnému výběru vhodných popisných statistik polohy (aritmetický průměr, medián, modus) a variability (směrodatná odchylka, kvantily) s ohledem na rozložení dat. Jsou přiblíženy základní typy rozložení – symetrické, sešikmené doprava, sešikmené doleva. Větší míra pozornosti je věnována normálnímu Gaussovu pravděpodobnostnímu rozložení a jeho statistickým vlastnostem. Jsou uvedeny příklady různých typů distribucí spojitých biomedicínských veličin.
Jsou popsány základní kroky testování hypotéz jako metody induktivní statistiky. Je vysvětlen rozdíl mezi parametrickými a neparametrickými statistickými testy. Parametrické metody pracují na základě parametrů normálního rozložení – průměru a směrodatné odchylky. Neparametrické testy pracují na základě pořadí. Přehledně jsou uvedeny různé druhy parametrických i neparametrických testů pro testování hypotéz pro spojité znaky. Opět je zdůrazněna nutnost správné volby parametrické či neparametrické metody.Klíčová slova:
popisná statistika – průměr – směrodatná odchylka – kvantil – normální Gaussovo rozložení – parametrické a neparametrické testyZPRACOVÁNÍ A ANALÝZA DAT
Nejčastější a nejzávažnější chybou při zpracování a analyzování dat je volba nesprávné metody. Nesprávnou volbou můžeme hned na počátku analýzy velmi snížit šanci na kvalitní výsledek. I v kvalitních odborných časopisech se totiž dnes můžeme setkat s nesprávně použitými statistikami. Někdy k takovým postupům vede i obava z připomínek recenzentů, kteří jsou například zvyklí charakterizovat všechna spojitá data pomocí průměru a směrodatné odchylky a vyžadují to i u dat, kde je použití těchto statistických ukazatelů přinejmenším diskutabilní.
Na počátku máme soubor dat, pro příklad uvažujme spojitou veličinu (například laboratorní hodnoty TAG, cholesterol, LDL, HDL, systolický či diastolický tlak krve atd.). Chceme-li tyto hodnoty prezentovat pomocí sumárních statistik středu a variability (rozptýlenosti), vybíráme z těchto možností – průměr, medián a modus pro charakteristiku střední polohy a směrodatná odchylka či kvantily pro charakteristiku variability dat.
Zabývejme se nejdříve prezentováním polohy dat neboli středu dat. Většina uživatelů statistiky sáhne po výpočtu aritmetického průměru. Je to ale vždy správně? Uvažujme dva soubory A, B s naměřenými hodnotami danými tabulkou 1. Připomeňme, že medián je frekvenční střed a platí, že polovina hodnot souboru je menší než medián a polovina hodnot je větší než medián. Modus je hodnota, která se v souboru hodnot vyskytuje nejčastěji.
Tab. 1. Příklady výpočtu charakteristik středu 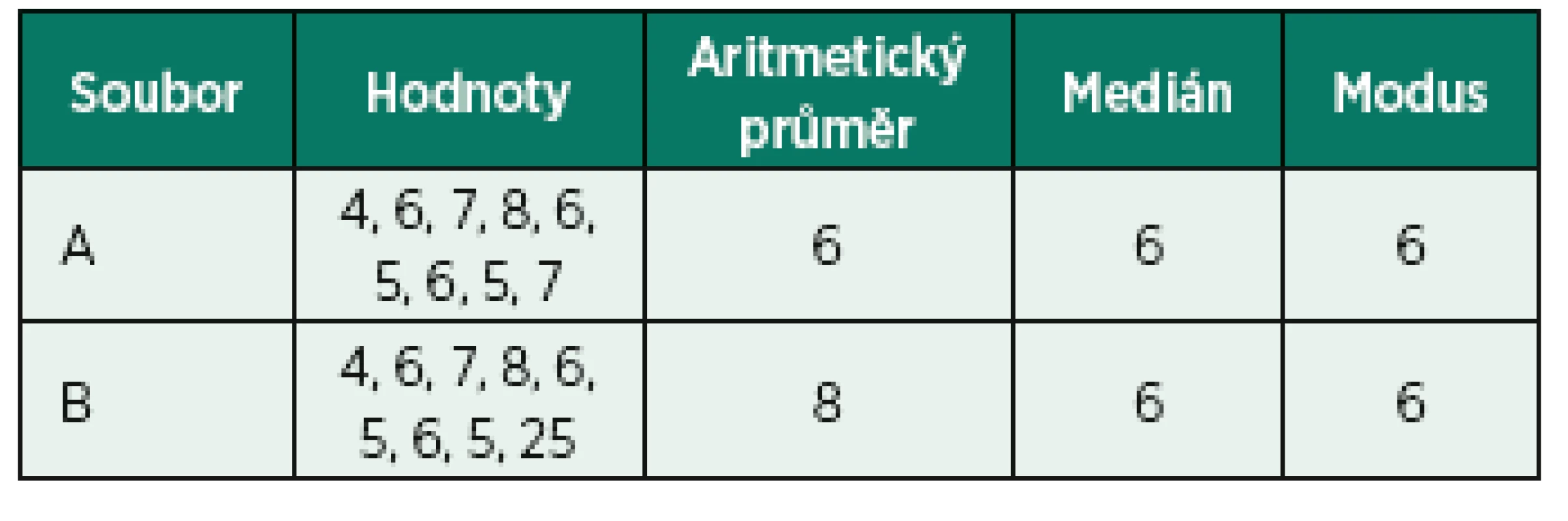
V souboru A jsou symetricky rozložené hodnoty a aritmetický průměr je stejný jako medián a modus. V souboru B je obsažena odlehlá hodnota (25) a aritmetický průměr je větší než medián či modus. Prvním krokem při výběru vhodné statistiky je tedy prohlídka četnostního tvaru a identifikace odlehlých hodnot. Prohlídka může probíhat i graficky, když si vytvoříme histogram četností. Podle tvaru četnostního rozložení (distribuce) dat rozeznáváme, zda je distribuce symetrická nebo asymetrická. Některé distribuce v medicíně jsou symetrické (např. tělesná výška). Je-li asymetrická (např. tělesná hmotnost nebo BMI), jde většinou o distribuci šikmou doprava. Většina distribucí je také jednovrcholová (unimodální), distribuce vícevrcholová je většinou způsobena nehomogenitou dat. Kdybychom například zkoumali distribuci tělesné výšky dospělých jedinců bez ohledu na pohlaví, bude mít distribuce dva vrcholy. Jeden vrchol bude u hodnoty průměrné výšky žen a druhý u hodnoty průměrné výšky mužů. V některých případech má rozložení dat více vrcholů, i když jsou data homogenní. Například distribuce utonulých osob podle věku je dvouvrcholová – 1. vrchol je u věku batolat a dětí do 4 let věku, 2. vrchol u věku dospívajících. Utonutí v dospělosti je méně časté.
Na obrázku 1 jsou zobrazeny tři základní modelové tvary distribuce dat.
Obr. 1. Základní typy distribuce spojitých znaků a odpovídající statistiky středu 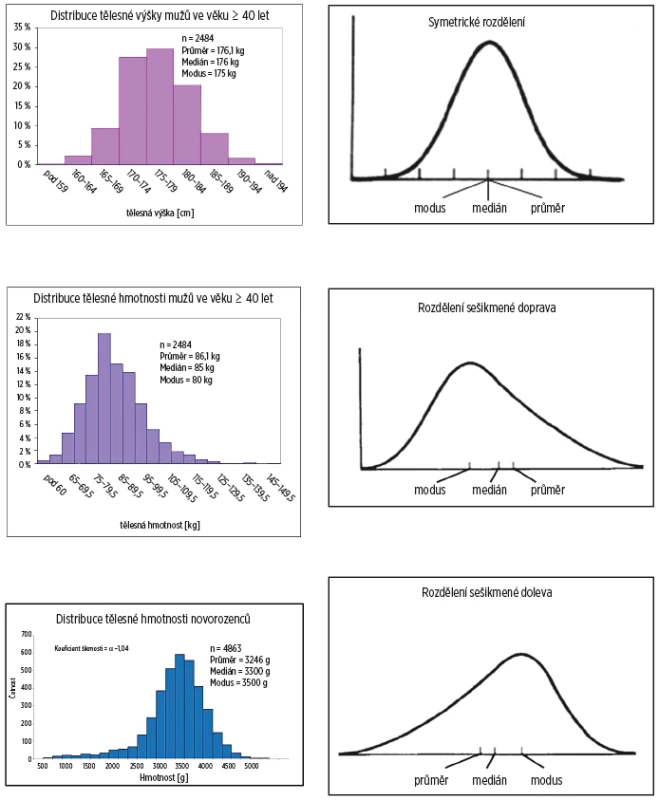
Význam a interpretace modu a mediánu se liší od průměru, neboť jejich význam zasahuje nejen naměřené hodnoty (čísla na ose X), ale také četnostní údaje na ose Y – tedy „kolikrát co bylo naměřeno“ a „kde jaká hodnota leží ve vztahu k dalším“. Naopak průměr je kvantitativní míra a jeho výpočet žádné řazení hodnot podle velikosti nevyžaduje. Průměr se frekvenčního výskytu hodnot netýká a z hlediska tvaru rozložení je doslova „slepý“. Objeví-li se mezi naměřenými hodnotami odlehlé číslo nebo číslo chybné až řádově odlišné, pak jeho přítomnost změní hodnotu mediánu jen minimálně (zvláště u větších souborů se na mediánu neprojeví vůbec). Avšak aritmetický průměr může zareagovat i velkým posunem, jak bylo patrné v příkladu u souboru B. Průměr pak není reprezentativním ukazatelem středu hodnot. Medián a podobné pořadové ukazatele proto nazýváme robustní statistiky, neboť nejsou citlivé na extrémní naměřené hodnoty. Rozdíl mezi hodnotami mediánu a průměru je známkou asymetrie rozložení dat nebo přítomnosti odlehlých hodnot. U asymetrických rozložení nebo při podezření na odlehlé hodnoty medián lépe charakterizuje střed rozložení než průměr [2].
V biomedicíně však nevystačíme pouze s ukazatelem středu, tento musí být vždy doplněn ukazatelem variability hodnot. Hovoříme o variabilitě primárních dat, která je vyjadřována tzv. mírami rozptýlenosti. U různých biologických znaků je přirozeně větší či menší variabilita, záleží samozřejmě i na podmínkách a metodice měření. U dat s vyšší mírou variability je obvykle obtížnější jejich správné měření a také se problematičtěji prokazují rozdíly, např. mezi zdravými a nemocnými jedinci. Nejčastěji používanou mírou rozptýlenosti je směrodatná odchylka, která se počítá jako kvadratický průměr odchylek hodnot znaku od jejich aritmetického průměru. Měli bychom mít na paměti, že její výpočet je smysluplný jen v případě, že rozložení hodnot odpovídá symetrickému normálnímu rozložení, které je charakterizované Gaussovou křivkou (obr. 2). Normální rozdělení pravděpodobnosti má dva parametry – populační průměr (μ), který určuje polohu na ose x, a populační směrodatnou odchylku (σ), která charakterizuje tvar (roztažení) zvonu. Pokud je variabilita dat (směrodatná odchylka) malá, je zvon úzký, pokud data vykazují vyšší míru variability, má zvon širší tvar. Jednou ze základních vlastností tohoto rozložení je, že v intervalu průměr ± směrodatná odchylka se nachází asi 68 % hodnot, v intervalu průměr ± 2 směrodatné odchylky leží přibližně 95 % všech naměřených hodnot a v intervalu průměr ± 3 směrodatné odchylky jsou obsaženy téměř všechny hodnoty. Na obrázku 3 je znázorněn četnostní histogram ukazující rozložení hodnot biochemické veličiny Triacylglyceroly (TAG) u 600 pacientů. Už z histogramu je patrné, že rozložení je sešikmené doprava, protože se zde vyskytují vysoké odlehlé hodnoty. Tyto hodnoty ovlivnily hodnotu průměru, který je vyšší než hodnota mediánu či modu. Také směrodatná odchylka je vlivem odlehlých hodnot vysoká, je dokonce vyšší než průměrná hodnota. Z tohoto je patrné, že charakterizovat takovou veličinu pomocí průměru ± směrodatné odchylky nedává smysl. Můžeme to porovnat s rozložením veličiny IQ (inteligenční kvocient) v populaci. Toto rozložení je normální a je dobře charakterizováno průměrem a směrodatnou odchylkou. Z grafu můžeme vyčíst, že 95 % populace má IQ mezi hodnotami 70–130 (průměr ± 2 směrodatné odchylky).
Obr. 2. Normální pravděpodobnostní rozložení 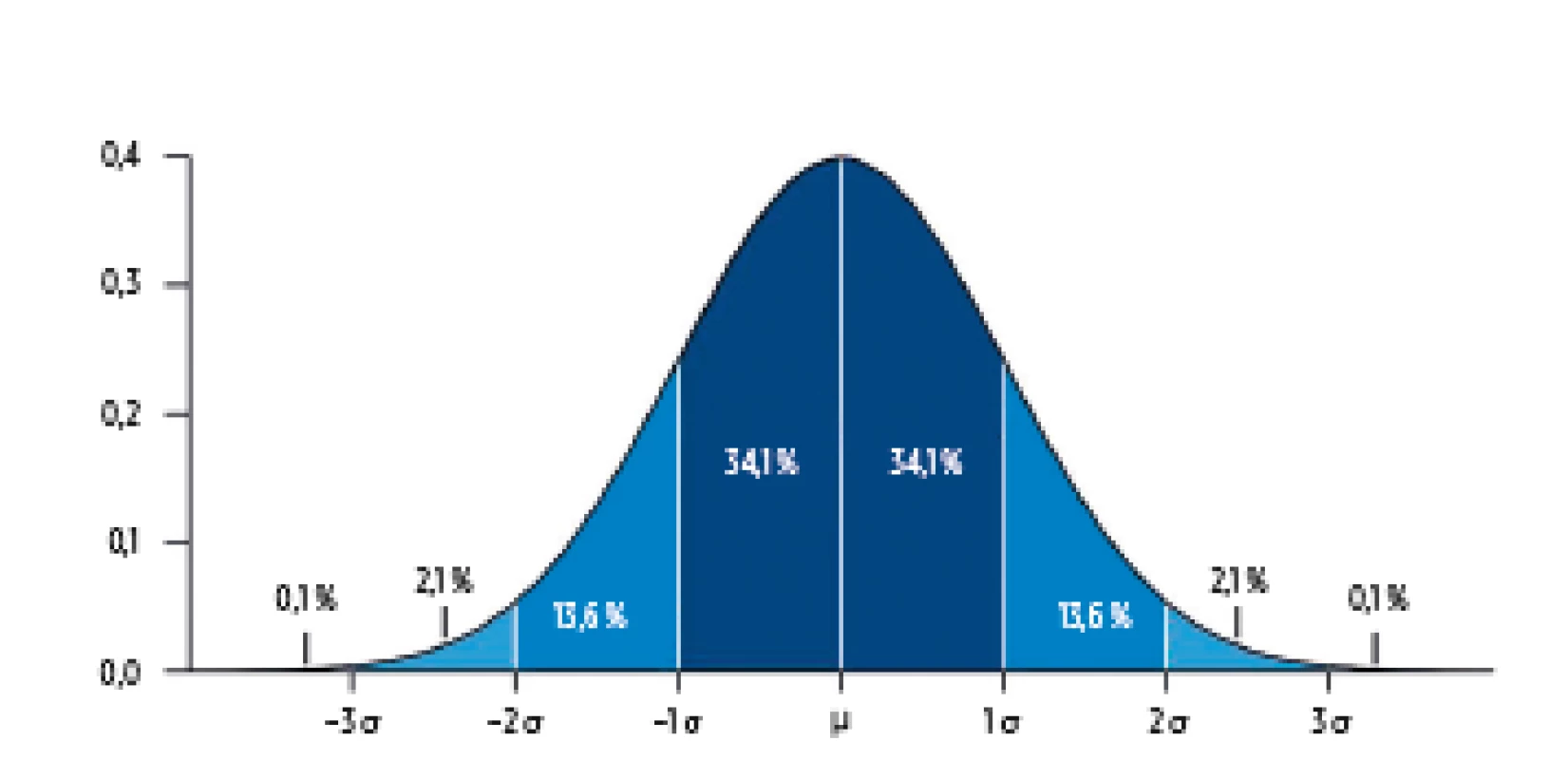
Obr. 3. Rozložení veličin TAG a IQ 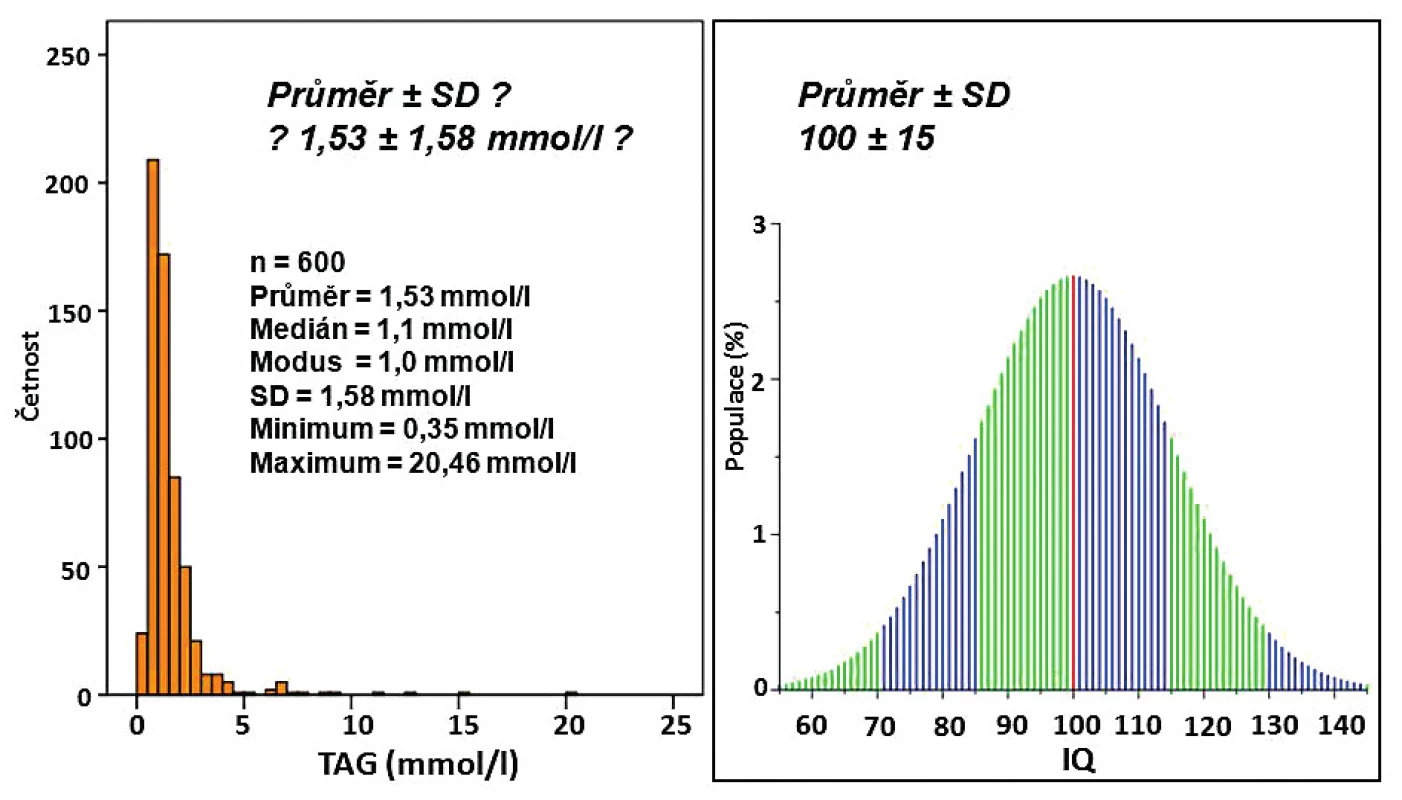
Jak tedy popsat variabilitu znaků, jejichž rozložení vykazuje podstatné odchylky od Gaussovy křivky? Ke slovu se opět dostávají tzv. robustní statistiky rozptýlenosti, které nevyžadují žádné předpoklady, kromě seřazení hodnot podle velikosti. Tyto tzv. pořadové statistiky typicky doplňují medián jako ukazatel středové tendence. Na výběr máme v této kategorii několik možností: nejjednodušším ukazatelem je výpočet minimální a maximální hodnoty, popř. jejich rozdílu, který se nazývá variační rozpětí. Pokud se v datech vyskytují odlehlé či extrémní hodnoty, může být i tento ukazatel zkreslující. Nejrozšířenější je proto počítání tzv. percentilů, což jsou statistiky, které procentuálně vyjadřují pořadí daného čísla v souboru. Pro 25% a 75% kvantil se používá speciální označení – dolní a horní kvartil. Jsou to hodnoty, pod nimiž leží 25 %, respektive 75 % menších hodnot. Můžeme je počítat vždy, když dokážeme data seřadit. Takže jsou použitelné i pro tzv. ordinální data. Ordinální data se nedají kvantifikovat, mají pouze význam jisté kvality, ale lze je přirozeným způsobem uspořádat. Typickým příkladem ordinálních dat může být například nejvyšší dosažené vzdělání (základní, středoškolské, bakalářské, magisterské, doktorské). Je zřejmé, že ordinální data neumožňují posoudit „vzdálenost“ jednotlivých kategorií nebo hodnot.
Když jsme data popsali, přistoupíme obvykle k testování hypotéz. Testování hypotéz je metoda induktivní statistiky, jejímž cílem je zobecňování výsledků výzkumu (tj. výsledků získaných z výběrových souborů) na celou populaci. Statistická hypotéza je tvrzení o celé populaci, jehož platnost se snažíme ověřit na základě dat získaných z náhodného výběru.
Nulová hypotéza (H0) představuje určitý rovnovážný stav a bývá vyjádřena rovností „=“ (H0: m = 100 – nulová hypotéza tvrdí, že průměrná populační hodnota daného parametru je rovna konstantě 100).
Alternativní hypotéza (HA) je tvrzení, které s nulovou hypotézou nesouhlasí, představuje porušení rovnovážného stavu a zapisujeme ji tedy jedním ze tří možných zápisů nerovnosti („≠“, „<“, „>“).
- Zvolíme-li alternativní hypotézu ve tvaru „<” nebo „>“, mluvíme o jednostranné alternativní hypotéze (např. μ < 100, μ > 100).
- Zvolíme-li alternativní hypotézu ve tvaru „≠”, mluvíme o oboustranné alternativní hypotéze (např. μ ≠ 100) [3].
Platnost statistické hypotézy se prověřuje pomocí statistického testu na základě dat naměřených ve výběrovém souboru. Opět se rozhodujeme mezi parametrickými a neparametrickými testy. Parametrické metody jsou založeny na počítání s průměry a směrodatnými odchylkami (tedy parametry normálního rozdělení), a proto základní předpoklad pro jejich použití je normální rozložení zkoumaných dat. Normalita dat se může ověřit vizuálně pomocí histogramu nebo můžeme použít některý z testů normality (např. Shapiro-Wilkův test nebo Kolmogorovův-Smirnovův test). Tyto testy jsou obsaženy v profesionálních statistických programech (Statistica, IBM SPSS Statistics, SAS, MedCalc, …). Když zjistíme, že kvantitativní veličina má normální rozdělení ve všech porovnávaných souborech, můžeme přistoupit ke statistickému testování pomocí parametrických metod. Uveďme si nejběžnější situace, které v biomedicínském výzkumu nastávají. Máme-li pouze jednu skupinu pacientů, u nichž jsme měřili hodnotu nějakého spojitého znaku (např. hladinu albuminu, Body Mass Index – BMI, celkový cholesterol atd.), můžeme pozorovanou průměrnou hodnotu porovnat s očekávanou populační hodnotou (např. s referenční hodnotou zjištěnou u zdravé populace). V této situaci můžeme použít jednovýběrový t-test. Pokud máme k dispozici dva nezávislé výběry (dvě různé skupiny pacientů nebo skupinu pacientů a kontrolní soubor) a chceme je porovnat v průměrných hodnotách spojité veličiny, použijeme dvouvýběrový t-test. Můžeme mít také jen jeden soubor pacientů, který měříme opakovaně (klasicky před léčbou a po léčbě), pak využijeme párového t-testu. U „párových“ dat je důležité, abychom je měli správně „spárované“, tedy aby výsledky prvního a druhého měření u daného pacienta byly v tabulce s daty uvedeny na jednom řádku. Toto zpracování není tedy použitelné u anonymního šetření, kdy nejsme schopni hodnotu z druhého měření přiřadit k odpovídající hodnotě z prvního měření. Když máme k dispozici tři a více nezávislých souborů a porovnáváme je opět v kvantitativní veličině, používáme analýzu rozptylu (analysis of variance – ANOVA).
Sílu závislosti mezi dvěma kvantitativními znaky (např. korelaci mezi věkem a diastolickým tlakem krve) můžeme změřit pomocí Pearsonova korelačního koeficientu (r) [1]. Přehledně jsou situace a k nim příslušné testy zaznamenány do tabulky 2:
Tab. 2. Použití parametrických metod v různých situacích 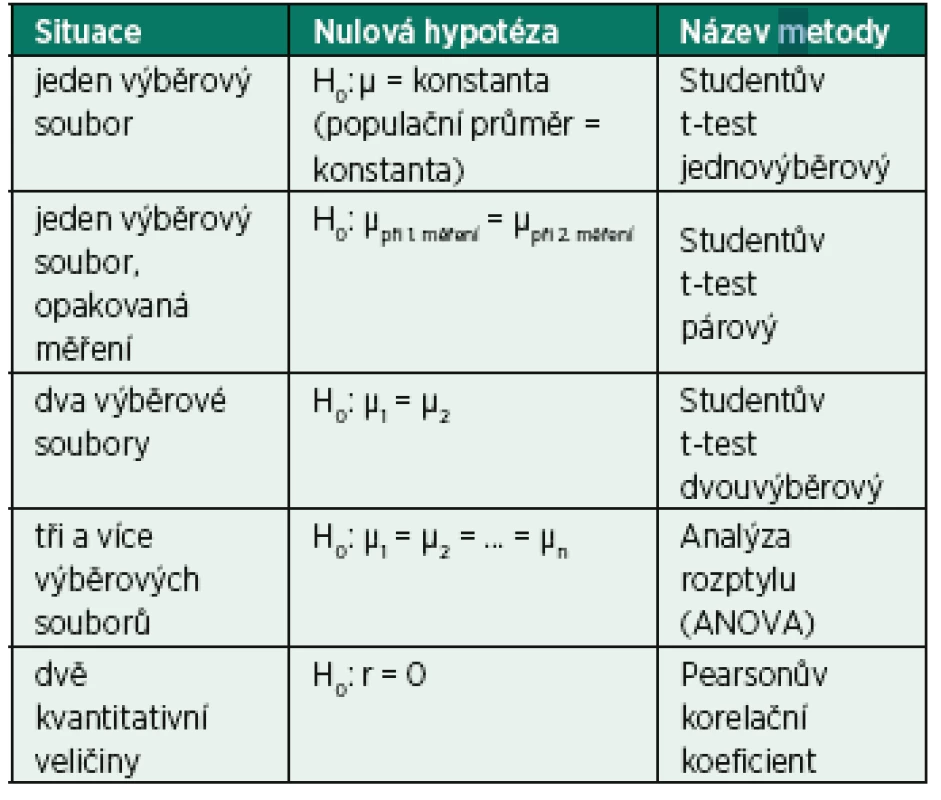
Když předpoklady normality splněny nejsou, dostávají se ke slovu neparametrické testy, které pracují na principu pořadí. Data jsou seřazena podle velikosti a primárním hodnotám jsou přiřazena pořadí. Neparametrické testy nepracují s konkrétními naměřenými hodnotami, ale pouze s jejich pořadovými hodnotami. Eliminuje se tak vliv extrémních a odlehlých hodnot, které zkreslují průměr a směrodatnou odchylku. Na druhé straně ale ztrácíme původní informaci – přesně naměřenou hodnotu. Tabulka 3 ukazuje přehled neparametrických metod, které se používají v analogických situacích jako parametrické metody.
Tab. 3. Přehled neparametrických metod 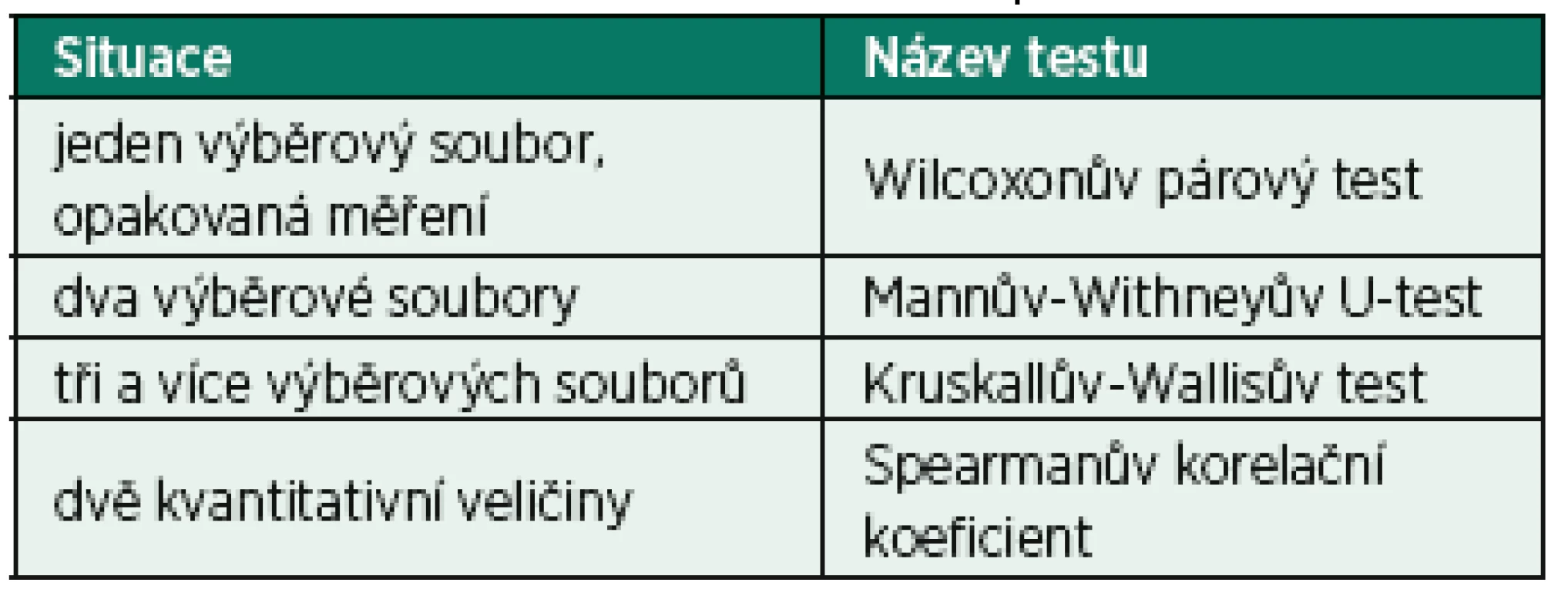
Závěrem můžeme říci, že používání parametrických metod ve statistice je zlatým standardem, protože tyto metody pracují s původními naměřenými hodnotami a neztrácejí žádnou informaci. Parametrické metody mají ale předpoklady o rozložení dat, za kterých mohou být použity. Pokud jsou předpoklady splněny, měly by být přednostně použity. Pokud ale předpoklad normality splněn není (např. kvůli existenci odlehlých hodnot nebo sešikmení rozložení), využijeme neparametrické metody. Musíme ale mít na paměti, že tyto metody nepracují s původními daty, ale s pořadími, a mají tedy o něco menší sílu než příslušné parametrické metody. To znamená, že mají nižší schopnost rozpoznat neplatnou nulovou hypotézu. Například nový lék je účinný, statisticky se ale účinek neprokáže. Tato skutečnost znamená, že pro prokázání statistické významnosti stejného rozdílu vyžadují větší velikost vzorku. Měli bychom na to myslet při plánování velikosti vzorku experimentu a přizpůsobit jeho velikost. Obvykle se doporučuje zvýšení velikosti vzorku o 10–15 %.
Práce je původní a nebyla publikována ani není zaslána k recenznímu řízení do jiného média.
Autoři prohlašují, že nemají střet zájmů v souvislosti s tématem práce.
Všichni autoři rukopis četli, souhlasí s jeho zněním a zasláním do redakce časopisu Anesteziologie a intenzivní medicína.
Práce byla prezentována formou přednášky na XXV. Šumperských dnech alergologie a klinické imunologie.
Poděkování: Práce byla podpořena grantovým projektem LO1304.
Do redakce došlo dne 11. 10. 2016.
Do tisku přijato dne 5. 1. 2017.
Adresa pro korespondenci:
Mgr. Kateřina Langová, Ph.D.
e-mail: katerina.langova@upol.cz
Zdroje
1. Altman DG. Practical Statistics for Medical Research. 1. vydání, 1991, 610 s., ISBN 0-412-27630-5.
2. Dušek L. Analýza dat v neurologii III. Nebojme se mediánu a robustních statistik. Cesk Slov Neurol N 2007;70/103 : 343–345.
3. Zvárová J. Základy statistiky pro biomedicínské obory. 1. vydání, 2004, 218 s. ISBN 80-7184-786-0.
Štítky
Anesteziologie a resuscitace Intenzivní medicína
Článek Zajímavosti, tipy a triky
Článek vyšel v časopiseAnesteziologie a intenzivní medicína
Nejčtenější tento týden
2017 Číslo 3- Jak souvisí postcovidový syndrom s poškozením mozku?
- Perorální antivirotika jako vysoce efektivní nástroj prevence hospitalizací kvůli COVID-19 − otázky a odpovědi pro praxi
- Metamizol v léčbě různých bolestivých stavů – kazuistiky
- Neodolpasse je bezpečný přípravek v krátkodobé léčbě bolesti
- Léčba akutní pooperační bolesti z pohledu ortopeda
-
Všechny články tohoto čísla
- Prohlášení výboru ČSIM na období 2017–2020
- Vybrané aspekty mezioborové spolupráce na porodním sále
- Pneumonie spojené se zdravotní péčí u pacientů v intenzivní péči – optimální nastavení iniciální empirické antimikrobiální terapie: výsledky multicentrické observační studie
- Energotrauma a ventilátorem indukované plicní poškození
- Jak do praxe aplikovat výsledky klinických studií?
- Epidemiologie mimonemocniční náhlé zástavy oběhu v České republice – národní výsledky studie EuReCa ONE
- Statistika v biomedicínském výzkumu II
- Alergie, anafylaxe, anafylaktický šok
- Klinická fyziologie vazopresinu
- Doporučený postup pro pooperační delirium
- Sepsis, it's been a hard year now…
- Mezinárodní doporučení pro postup u pacientů se sepsí a septickým šokem
- Stanovisko výboru České společnosti intenzivní medicíny ČLS JEP k používání nové definice sepse („Sepsis-3“)
-
Anestezie v Rakousko -Uhersku během I. světové války a po vzniku samostatného československého státu
Část I - Úvod - Zajímavosti, tipy a triky
- Anesteziologie a intenzivní medicína
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Mezinárodní doporučení pro postup u pacientů se sepsí a septickým šokem
- Doporučený postup pro pooperační delirium
- Epidemiologie mimonemocniční náhlé zástavy oběhu v České republice – národní výsledky studie EuReCa ONE
- Alergie, anafylaxe, anafylaktický šok
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání



