Nejistoty výsledků měření

Souhrn

Každý výsledek měření je doprovázen nejistotou, která vyjadřuje principiální nemožnost provést absolutně přesné měření. Výsledkem měření proto není (nemůže nikdy být) jediné číslo. Výsledkem měření je vždy interval (oblast hodnot), ve kterém se skutečná hodnota nachází s určitou pravděpodobností. Nejistotní přístup představuje nejenom aktuální pohled teorie měření (metrologie) na proces a výsledky měření, ale je též implementován do všech moderních norem a systémů řízení kvality. Znalost nejistoty výsledku měření poskytuje jak subjektu, který provádí měření, tak zákazníkovi (příjemci výsledku) základní představu o kvalitě výsledku. Tento text se zabývá objasněním pojmu nejistoty doprovázející výsledek měření a tím, jak se její existence promítá do rutinní práce lékařů a laboratoří.

klíčová slova:

měření – výsledek – nejistota

ZÁKLADNÍ PRINCIP

Začněme kategorickým a nesmlouvavým prohlášením:

Nejistota doprovází každý výsledek měření. Opravdu každý.

Jinými slovy, neexistuje absolutně přesný výsledek, a to bez ohledu na to, co měříme, kolik času měření věnujeme, nebo jak drahou použijeme instrumentaci. Koncepce nejistot vychází ze základního předpokladu, že náhodné chyby, doprovázející měření, mají Gaussovo rozdělení s nulovou střední hodnotou a nenulovým rozptylem. Gaussova křivka popisuje závislost hustoty pravděpodobnosti (osa y) na velikosti náhodné chyby (osa x), jak ukazuje obrázek 1.

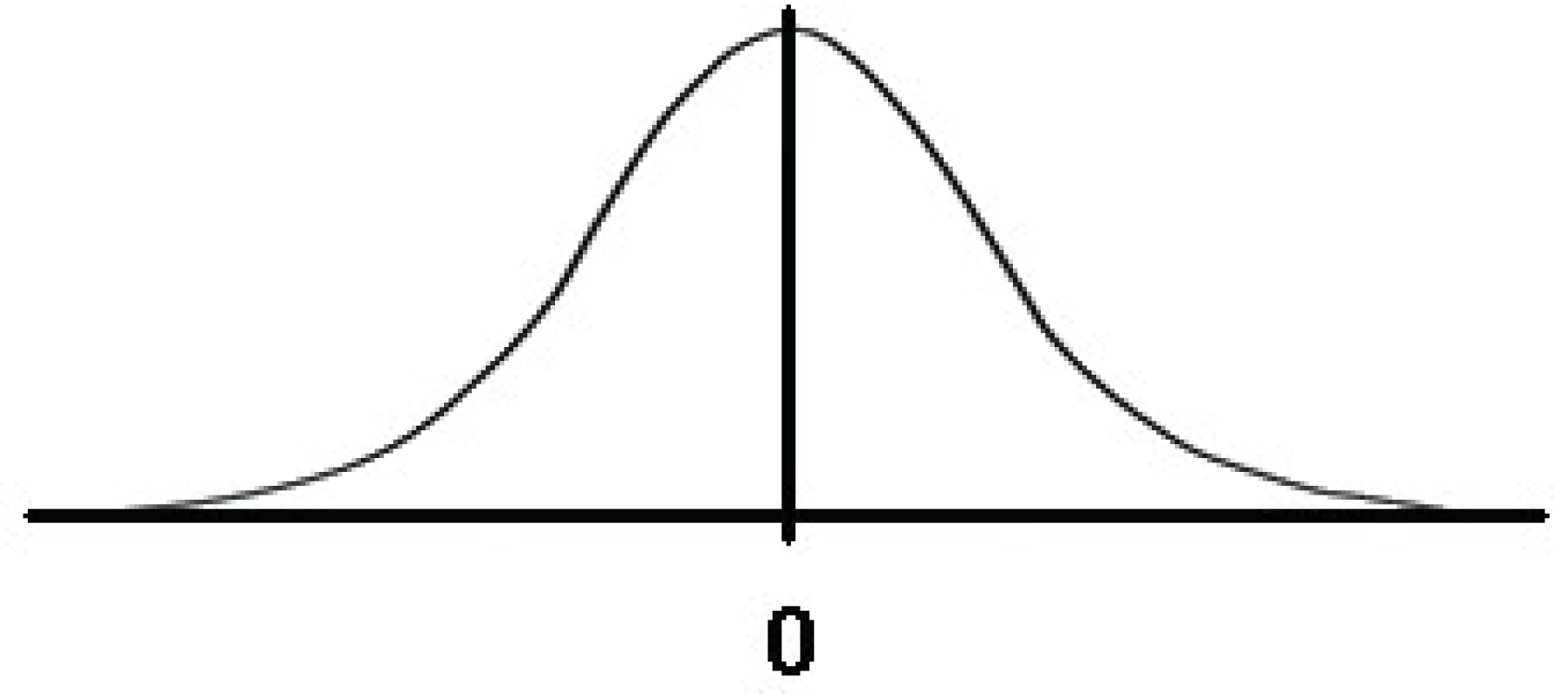
Interpretace je velmi intuitivní: Malé chyby (blízké nule) jsou mnohem pravděpodobnější než větší chyby (vzdálené od nuly vlevo/záporné či vpravo/kladné). Pravděpodobnost velkých chyb je sice malá, ale nenulová, a proto je nelze vyloučit. Se zvětšující se velikostí chyby tedy klesá její pravděpodobnost.

Pravděpodobnost toho, že se náhodná chyba nachází v určitém intervalu, je dána velkostí plochy ohraničené Gaussovou křivkou a hranicemi tohoto intervalu. Celková plocha pod Gaussovou křivkou (od -∞ do +∞) je 1 (tedy 100 %), což nám říká, že máme jistotu, že chyba se nachází mezi -∞ a +∞. Tato jistota je sice pěkná, ale prakticky pro nás nepřináší žádný užitek – k užitečným informacím se dopracujeme dále v textu. Avšak jeden zásadní poznatek je patrný ihned: Koncepce nejistot je aplikací pravděpodobnostního modelu, což můžeme jinými slovy vyjádřit tak, že neexistuje žádné kritérium, kterým bychom výsledky měření mohli rozdělit na správné a nesprávné – vždy můžeme mluvit pouze o tom, že „správný výsledek“ leží s určitou pravděpodobností v nějaké oblasti. Pojmem „správný výsledek“ zde rozumíme výsledek, který se co nejvíce přibližuje skutečné (pravé) hodnotě měřené veličiny.

Už samotná představa toho, že absolutně přesný výsledek měření nelze z principu získat, může vzbuzovat určitou „nedůvěru“ k výsledkům měření obecně, a tedy i k výsledkům získaným v klinických laboratořích. Nejistota je právě tím parametrem, který pro nás může být měřítkem důvěryhodnosti a použitelnosti konkrétního výsledku měření.

Výše uvedené skutečnosti se pokusíme na dalších řádcích objasnit a demonstrovat na několika jednoduchých příkladech tak, aby čtenář mohl sám posoudit, zda a jak nejistota výsledků měření ovlivňuje jeho každodenní práci a rozhodnutí, která na podkladě výsledků měření činí. Cílem sdělení je názorně demonstrovat koncepci a nikoli zabřednout do přílišných detailů nebo matematických a terminologických spletitostí. Tím se vědomě dopouštíme některých zjednodušení, avšak tuto oběť přinášíme v zájmu srozumitelnosti a přehlednosti (komplexnější pojednání o nejistotách zpravidla čítají stovky stran textu – základní dokument představuje [1], řadu definic a terminologických detailů lze nalézt v literatuře [2]).

Příklady, které níže uvádíme, nejsou smyšlené – opíráme se zde o reálné údaje, které klinické laboratoře uvádějí v rámci systému externího hodnocení kvality (EHK) a které jsou volně dostupné [3].

ZÁSADNÍ DŮSLEDEK EXISTENCE NEJISTOTY

Přítomnost nejistoty doprovázející každý výsledek měření vyjadřuje principiální nemožnost provést absolutně přesné měření. Základním důsledkem, který s sebou existence nejistoty přináší, je skutečnost, že výsledkem měření není (nemůže nikdy být) jediné číslo. Výsledkem měření je vždy interval (oblast hodnot), ve kterém se skutečná hodnota nachází s určitou pravděpodobností.

Rozdílnost dvou možných pohledů na výsledek měření ukazuje obrázek 2.

Fakt, že naprostá většina výsledků měření, se kterými se v každodenním životě setkáváme, je prezentována formou jediného čísla, není důkazem „neexistence nejistoty“, ale důsledkem toho, že nejistota není jako součást výsledku měření běžně uváděna, a to z důvodu zjednodušení komunikace (je tedy tiše zamlčena).

Detailnější pohled

Nejistota výsledku měření se běžně označuje symbolem U_c, kde velké U (ze slova uncertainty) znamená, že jde o rozšířenou nejistotu a index C říká, že jde o kombinovanou nejistotu. Oba pojmy zasluhují krátké vysvětlení, avšak ještě před tím, než k němu přikročíme, učiníme malou odbočku.

Nejistotu konkrétního výsledku měření nelze nikdy určit z pouhého jednoho provedeného měření. Aby bylo možné nejistotu vypočítat, je třeba provést větší počet měření (např. 10) daného konkrétního vzorku. Tento postup je běžný u kalibračních nebo referenčních laboratoří, avšak rutinní klinické laboratoře provádějí standardně jedno měření (z časových a ekonomických důvodů). Kde se tedy vzala nejistota, kterou pro daný typ měření (metodu) prezentují klinické laboratoře svým zákazníkům – klinikům? Jedná se o tzv. odhad nejistoty. To znamená, že konkrétní laboratoř jednou za čas (zpravidla 1krát ročně) spočítá pro každou ze svých metod velikost nejistoty [4], která doprovází výsledky měření získané touto metodou a takto získaný výsledek (odhad nejistoty) pak v následujícím roce prezentuje svým zákazníkům. V tomto textu mluvíme o rutinních klinických laboratořích, proto rozumíme pod „nejistotou“ ve skutečnosti její odhad.

Nyní se vraťme k popisu symbolu U_c, kterým se označuje rozšířená kombinovaná nejistota. Tato nejistota nám říká, v jaké oblasti (v jakém okolí naměřené hodnoty) se skutečná hodnota nachází s pravděpodobností 95 %.

V tomto textu rozumíme pod zkráceným označením „nejistota“ vždy rozšířenou kombinovanou nejistotu.

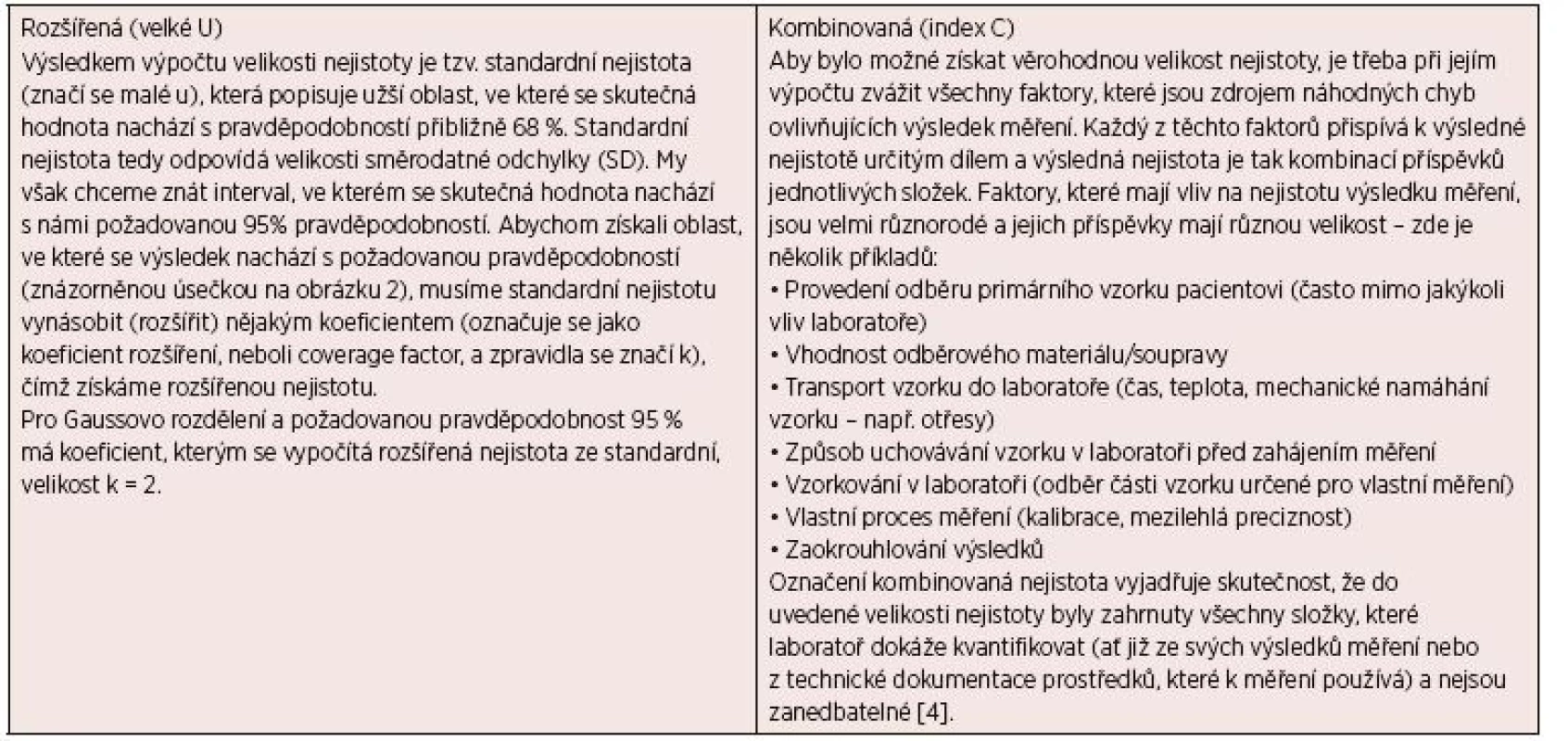
Praktický příklad

Jako příklad použijeme měření počtu leukocytů v klinické laboratoři. Běžný laboratorní výsledek může mít např. takovouto podobu:

Leukocyty 5,40 x 10⁹/l

My už ale víme, že toto nemůže být (celá) pravda – je to zjednodušení, protože nám byla zamlčena nejistota tohoto výsledku. Ta se u měření počtu leukocytů běžně pohybuje okolo U_c = 5 % (jak to víme a že nejistota se v závislosti na konkrétní laboratoři může významně lišit, to ukážeme později v subkapitole Potíže s určením velikosti nejistoty).

Pokud tedy víme, že výše uvedený výsledek je zatížen nejistotu o velikosti U_c = 5 %, můžeme jej zapsat podstatně přesněji a věrohodněji takto (všechny 3 zápisy jsou ekvivalentní):

1. Leukocyty 5,40 x 10⁹/l ± 5 %
2. Leukocyty 5,40 x 10⁹/l ± 0,27 x 10⁹/l
3. Leukocyty (5,40 ± 0,27) x 10⁹/l

Co nám tento zápis výsledku říká o skutečné hodnotě?

Skutečná hodnota (tj. ten absolutně správný výsledek, který z principu nedokážeme nikdy zjistit) se s pravděpodobností 95 % nachází v intervalu 5,13 až 5,67 x 10⁹/l. A špatná zpráva je, že existuje malá pravděpodobnost (konkrétně 5%), že skutečná hodnota leží mimo uvedený interval. Lze tedy říci, že nejistota představuje určitou kvantifikaci kvality nebo důvěryhodnosti výsledku měření a možná bude pro čtenáře překvapením, že i výsledky s nejistotou blížící se 100 % mohou být důvěryhodné a jsou v medicíně zcela běžně využívány, jak uvidíme dále.

Vizualizaci tohoto příkladu ukazuje obrázek 3.

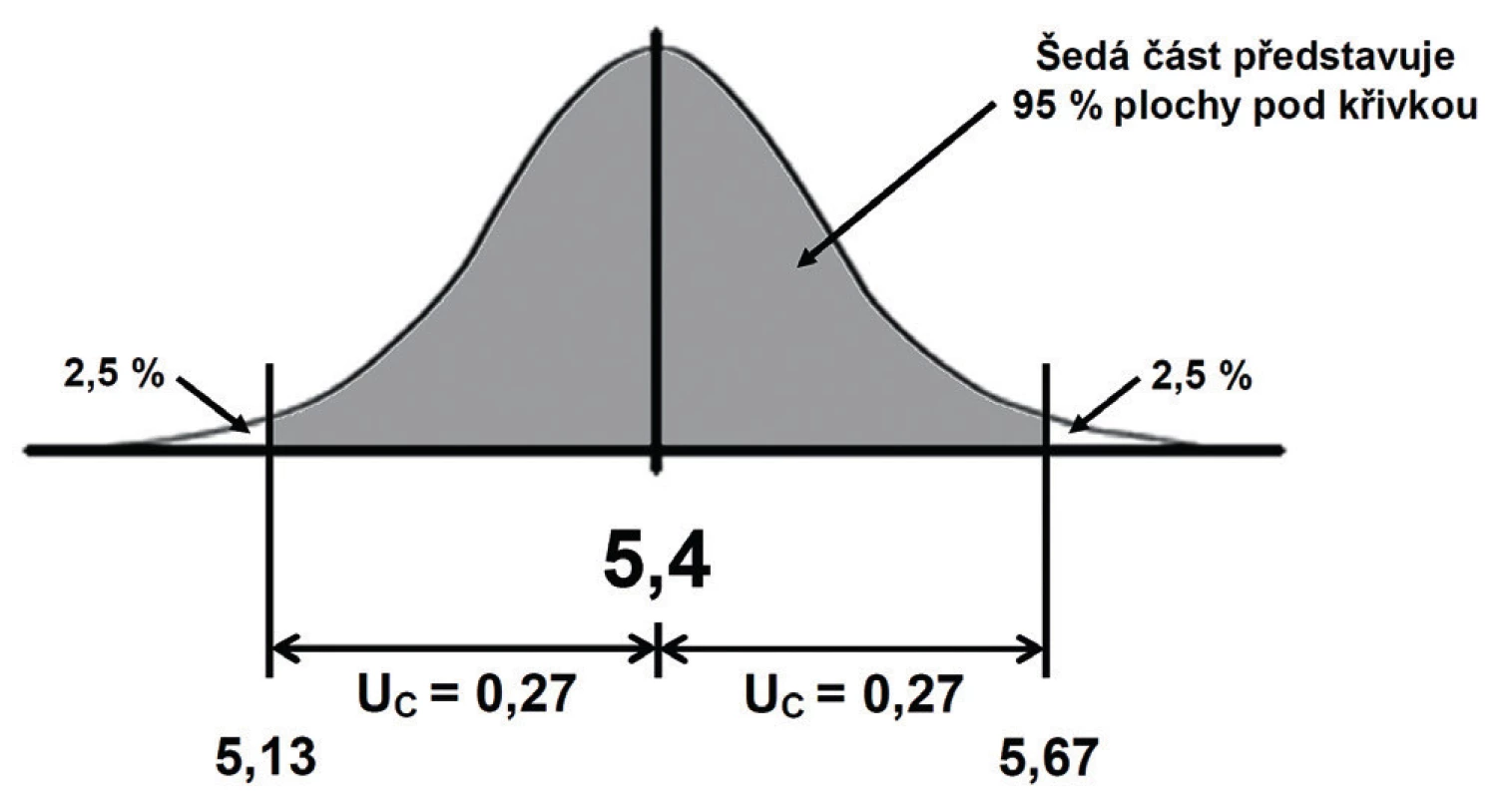
Pravděpodobnost toho, že se skutečný výsledek nachází v určitém intervalu, je dána velikostí plochy ohraničené Gaussovou křivkou a hranicemi tohoto intervalu. A speciální vlastností rozšířené kombinované nejistoty (U_c) je to, že se jedná právě o číslo, které z uvedené plochy vytne oblast 95 %, a proto konstatujeme, že skutečný výsledek se nachází s pravděpodobností 95 % v intervalu ±U_c okolo naměřené hodnoty. Je důležité si uvědomit, že rozložení pravděpodobnosti v intervalu určeném naměřenou hodnotou a její nejistotu není rovnoměrné – hodnoty v blízkosti naměřené hodnoty jsou pravděpodobnější než hodnoty u okrajů tohoto intervalu. Zůstává zde však 2,5 % pravděpodobnost, že skutečný výsledek leží pod takto určeným intervalem (a stejně tak nad ním) – viz označené bílé plošky na obrázku 3.

Co nejistota je

Nejistota výsledku měření představuje kvantifikaci našich (principiálně) omezených možností při měření a říká nám že:

• Skutečná hodnota se s pravděpodobností 95 % nachází v intervalu, v jehož středu leží naměřená hodnota (výsledek měření) a který sahá do vzdálenosti ±U_C okolo naměřené hodnoty. Naměřená hodnota je přitom nejlepším dostupným odhadem skutečné hodnoty.
• Jinými slovy můžeme situaci popsat tak, že kdyby laboratoř měření našeho vzorku opakovala (nezapomínejme, laboratoř měřila jen jednou), tak by se 95 % výsledků těchto opakovaných měření nacházelo v uvedeném intervalu.

Co nejistota není

Nejistota není chyba. Nejistotu (U_c) není možné zaměňovat s celkovou chybou (TE, total error), která představuje koncepčně odlišný přístup. Úlohou nejistoty není určit celkovou chybu konkrétního výsledku měření, ale identifikovat možné zdroje rozptylu výsledků měření v dané laboratoři, tyto zdroje kvantifikovat a na základě této analýzy přiřadit jednotlivému výsledku měření oblast pravděpodobného výskytu skutečné hodnoty. Nejistota nám – bohužel – nedává jistotu, že se skutečná hodnota nachází v intervalu ±U_C, ale říká, že se v něm nachází s rozumnou pravděpodobností.

Absolutní a relativní nejistoty

Jak bylo uvedeno výše, není nejistota z praktických důvodů uváděna jako součást každého jednotlivé-ho výsledku měření. Avšak každá akreditovaná klinická laboratoř je povinna znát nejistoty (odhady nejistot) výsledků měření, které odesílá svým zákazníkům [5].

V případě, že z laboratoře obdržíme výsledek:

Leukocyty 5,40 x 10⁹/l

a zajímá nás jeho nejistota, lze ji zjistit v příslušné laboratoři (na jejím webu, telefonicky apod.) – laboratoř pak poskytne (je povinna poskytnout) doplňující informaci o nejistotě např.:

U_c,rel = 5 % pro nejistotu vyjádřenou relativně (v %)

nebo

U_c,abs = 0,27 x 10⁹/l pro nejistotu vyjádřenou v absolutních jednotkách

Oba způsoby vyjádření jsou korektní a přípustné. Avšak ostražitost je na místě, protože nejistota sdělená laboratoří může ukrývat záludnost, která nemusí být patrná na první pohled. Předpokládejme, že z laboratoře obdržíme výsledek:

Faktor XII 47,5 %

a na dotaz ohledně jeho nejistoty laboratoř odpoví:

U_c = 8 %

Co to ale znamená? Nachází se skutečná hodnota v intervalu 47,5 ± 3,8 % nebo 47,5 ± 8 %? To nelze rozhodnout. Jediným východiskem je, že laboratoř explicitně uvede, zda jde o relativní (U_c,rel) nebo absolutní (U_c,abs) nejistotu. Tento explicitní popis, zda byla uvedena nejistota vyjádřená relativně nebo absolutně, je zásadní v případech, kdy jsou výsledky měření vydávány v procentech. Jedná se o další argument hovořící proti používání procent v roli jednotek u výsledků měření (zásadním argumentem je samozřejmě to, že % není SI jednotka) – proti této argumentaci ale stojí zažité zvyklosti.

Kritéria pro velikost nejistoty

Jak bylo uvedeno výše, představuje nejistota výsledku měření určitý ukazatel kvality tohoto výsledku. Naše přirozené očekávání „co nejpřesnějších výsledků“ můžeme jinými slovy vyjádřit tak, že požadujeme výsledky s co nejmenší nejistotu. Již víme, že nejistota nemůže být nulová (absolutně přesný výsledek neexistuje), ale ukážeme si, že i požadavek na „co nejmenší“ nejistotu není rozumný a v principu je vhodné požadovat, aby výsledek měření byl zatížen takovou nejistotou, která vyhovuje zamýšlenému použití tohoto výsledku.

Jako příklad můžeme uvést vážení, tedy měření hmotnosti: Pokud vážíme dospělého jedince, jistě se spokojíme s výsledkem, který je zatížen nejistotou U_c = 0,1 kg, tedy např. (68,5 ± 0,1) kg. Avšak takováto nejistota by nám jistě nevyhovovala při vážení novorozenců, kde budeme téměř jistě požadovat nejistotu přibližně o řád nižší, tedy U_c = 0,01 kg. A naše nároky vzrostou o několik řádů, pokud budeme pracovat s analytickými váhami, kde budeme požadovat nejistotu např. U_c = 0,00001 kg.

Je zřejmé, že zmenšování nejistoty (tedy zlepšování kvality výsledku) s sebou nese jeden podstatný vedlejší efekt – zvyšování ceny a/nebo času potřebného k získání výsledku zatíženého menší nejistotou.

Potíže s určením velikosti nejistoty

Podmínky v různých laboratořích jsou různé, proto nelze definovat jednoduchý univerzální návod na určení velikosti nejistoty (text [1] je sice univerzální, stěží však lze tvrdit, že je jednoduchý). Každá laboratoř musí sama rozhodnout, jaké složky do výsledné kombinované nejistoty zahrne a sama musí tyto složky kvantifikovat. Důsledky této skutečnosti ukazuje obrázek 4. Opět jde o reálná data získaná v rámci EHK, kde účastníci kromě vlastního výsledku měření uvádějí i jeho nejistotu (relativní, tedy v %). Všech 106 laboratoří měřilo stejný vzorek (počet leukocytů byl 17,6 x 10⁹/l – této hodnotě odpovídá centrální vodorovná čára 100 %; další dvě vodorovné linie na pozicích 84,7 % a 115,3 % vymezují kritéria EHK – tedy pás, ve kterém byly výsledky účastníků hodnoceny jako úspěšné) a všechny laboratoře měřily pomocí automatů. Na první pohled je vidět, že se nejistoty uváděné jednotlivými laboratořemi mohou významně lišit – velikost úsečky (tj. nejistoty) laboratoře 2 je asi 25krát větší, než nejistota uváděná laboratoří 1.

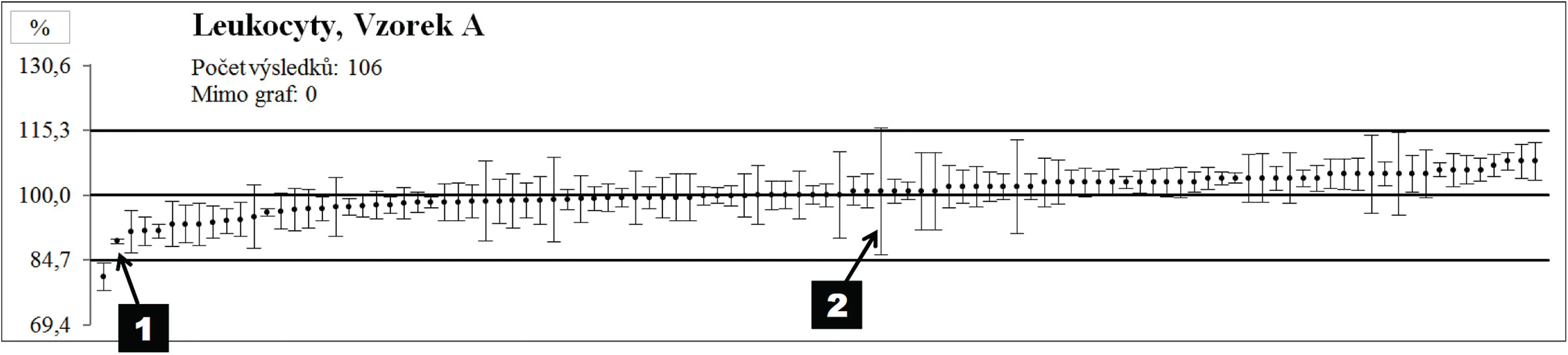
Co to znamená? Opravdu laboratoř 2 poskytuje výsledky s 25krát horší (větší) nejistotu než laboratoř 1? Teoreticky to nelze vyloučit, avšak jako pravděpodobnější se jeví vysvětlení, že laboratoř 1 nejistotu svých výsledků vypočítala špatně. Nelze si totiž nevšimnout, že jí udávaná velikost nejistoty je mnohonásobně menší nejenom ve srovnání s laboratoří 2, ale i ve srovnání s většinou dalších laboratoří. A protože tato laboratoř používá podobnou instrumentaci jako řada dalších pracovišť, je jí uváděná řádově menší nejistota velmi nepravděpodobná.

Jak je to možné? Velmi časté jsou 3 chyby (nebo jejich kombinace):

1. Záměna jednotek (konkrétně v tomto případě laboratoř uvedla U_c = 0,59 % pro výsledek 15,7 x 10⁹/l a lze spekulovat, že ve skutečnosti šlo o absolutní nejistotu U_c = 0,59 x 10⁹/l, ze které bychom přepočtem získali podstatně realističtější relativní nejistotu U_c = 3,8 %).
2. Záměna standardní a rozšířené nejistoty (menší – standardní – nejistota je chybně vydávána za rozšířenou, aniž by byla vynásobena koeficientem k = 2).
3. Do výpočtu nejistoty nejsou zahrnuty všechny podstatné složky (úloha jejich identifikace není jednoduchá a neexistuje návod, který by klinickým laboratořím jasně řekl: do kombinované nejistoty musíte vždy zahrnout 5 složek).

Naprostá většina laboratoří z grafu na obrázku 4 uvádí velikost nejistoty mezi 4 a 6 %, a proto jsme v našem příkladu výše použili jako obvyklou velikost nejistoty pro měření počtu leukocytů U_c = 5 %. Obrázek 4 ale jasně ukazuje, že velikosti nejistot v různých laboratořích se liší. Rozdílné velikosti nejistot mohou charakterizovat nejenom různé schopnosti laboratoří měřit, ale také různé schopnosti správně určit velikost nejistoty. Je profesionální odpovědností každé laboratoře, aby nejistoty svých výsledků určila pečlivě a zodpovědně. Klinik se na údaje z laboratoře spoléhá a důvěřuje jim, protože nemá žádnou možnost, jak by si mohl „věrohodnost“ nejistoty ověřit.

Pro jedno konkrétní laboratorní vyšetření prováděné v jedné laboratoři existuje zpravidla více nejistot

Každá laboratoř je schopna konkrétní měření provádět v určitém rozsahu, který označujeme jako měřicí rozsah (ten je zdola ohraničen tzv. mezí stanovitelnosti označovanou LoQ – limit of quantification). Měřicí rozsah je dán vlastnostmi konkrétního měřicího systému a nikdy nesahá od 0 do ∞. Navíc i v rámci daného měřicího rozsahu je prakticky vyloučeno, aby všechny výsledky měly stejnou (nebo velmi podobnou) nejistotu. Výsledky s nejmenší nejistotu jsou zpravidla získávány v oblasti referenčního intervalu a nejistota výsledků, které se od tohoto intervalu vzdalují, zpravidla roste. Zejména strmý nárůst nejistoty pozorujeme obvykle u velmi nízkých výsledků.

Abychom situaci dokumentovali konkrétně, vrátíme se opět k měření počtu leukocytů. Mějme analyzátor, kde výrobce uvádí pro měření počtu leukocytů měřicí rozsah 0,0 až 250,0 x 10⁹/l. Dále uvádí, že pro výsledky větší než 250 systém ohlásí překročení měřicího rozsahu a uvádí rovněž preciznost měření vyjádřenou variačním koeficientem CV = 2,5 %.

Již zde můžeme narazit na problém, pokud si položíme otázku, co znamená údaj LoQ = 0,0 – mohl by vzniknout nesprávný dojem, že systém měří „od nuly“ (a je tedy schopen změřit např. jeden leukocyt v jednom litru). Zde je důležité věnovat pozornost počtu platných číslic – systém zjevně zaokrouhluje výsledky na jedno desetinné místo, a pokud tedy vydá výsledek 0,0, je skutečná hodnota počtu leukocytů < 0,05 x 10⁹/l (tedy jakýkoli počet menší než 50 000 000 leukocytů na litr je prezentován jako výsledek 0,0).

Fakta, která máme k dispozici, můžeme orientačně znázornit pomocí následujících 2 grafů. Na ose x je vždy skutečná hodnota a na ose y je naměřený výsledek – v levém grafu jde o výsledek v absolutních jednotkách, v pravém je výsledek měření vyjádřen jako procento skutečné hodnoty. Ideální průběh závislosti naměřeného výsledku na skutečné hodnotě je označen čárkovaně. Červeně je vyznačena skutečnost odpovídající údajům výrobce a modře je naznačen odhad nejistoty výsledků měření zkonstruovaný z dat uvedených výrobcem (jelikož nic dalšího nevíme, odhadneme nejistotu jako dvojnásobek preciznosti, tedy U_c = 5 %). Zkratkou RI je zeleně vyznačena oblast referenčního intervalu. Měřítko grafů je samozřejmě (hrubě) zkreslené tak, aby dobře znázorňovaly princip.

Obrázek 5 (pro přehlednost vynecháváme u údajů o počtu „x 10⁹/l“) dokumentuje potíže, které obecně vznikají při měření poblíž meze stanovitelnosti. Náš systém pro skutečné hodnoty do 0,05 vydává výsledek 0,0, tedy výsledek s relativní chybou – 100 %, jakmile počet leukocytů ve vzorku dosáhne 0,05, objeví se na displeji výsledek 0,1, tedy výsledek s relativní chybou +100 %. Už jenom v důsledku zaokrouhlování je červená čára v levé části grafu v blízkosti meze stanovitelnosti velice „zubatá“ (ještě více, než schematický obrázek 5 ukazuje) a je jisté, že nejistota výsledku měření v řádu jednotek procent (modrá čára) je zde naprostou utopií a zcela bezpochyby bude dosahovat (i v důsledku dalších vlivů) desítek procent.

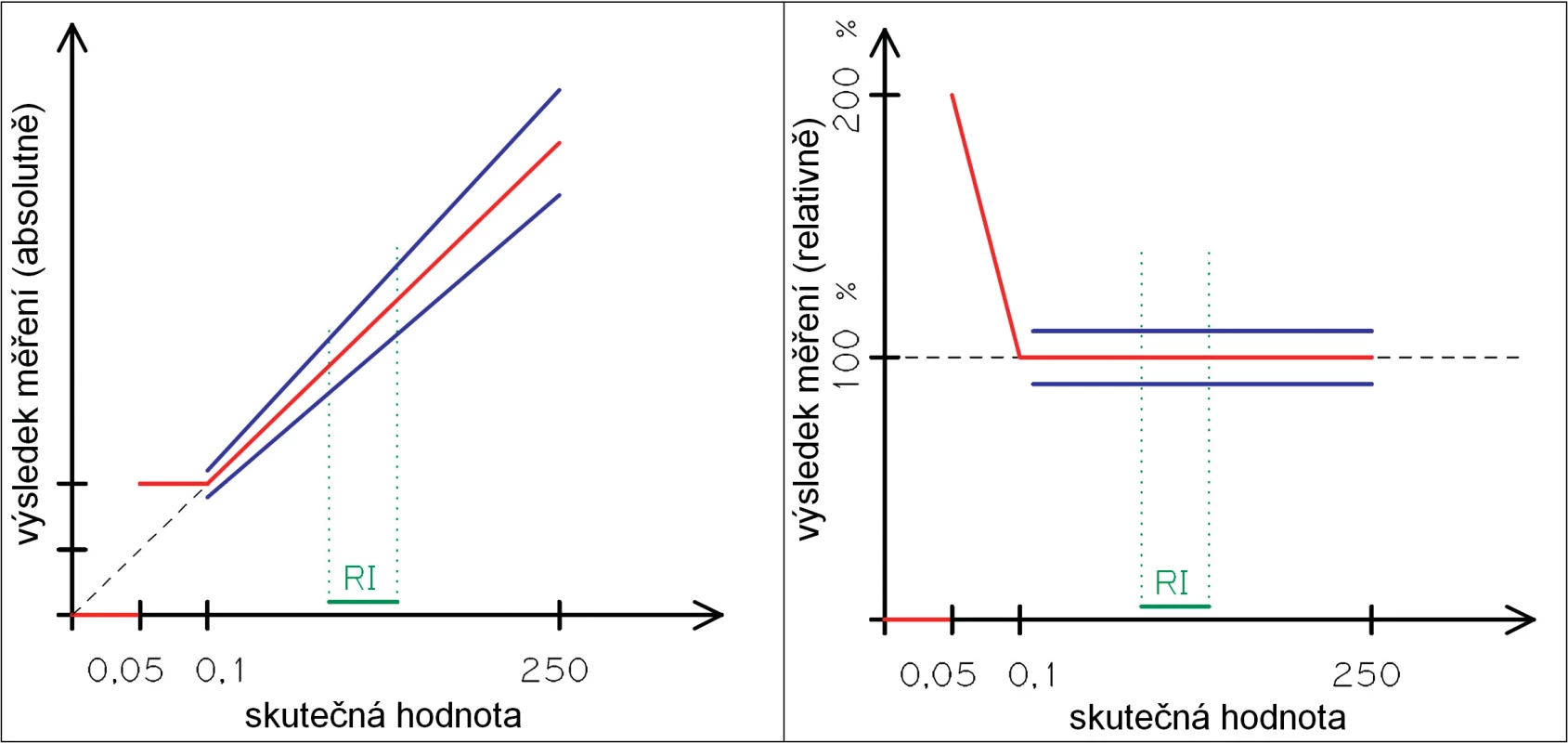
Jakkoli můžeme být uvedenými skutečnostmi zděšeni, je třeba si položit pragmatickou otázku: Koho to zajímá?

Zde je naprosto zásadní podívat se znovu na obrázek a uvědomit si, že výsledky měření, jejichž nejistota je v řádu desítek procent, jsou velmi vzdáleny od oblasti referenčního intervalu, tedy velká nejistota se týká výsledků měření, které se u běžných pacientů prakticky nikdy neobjeví.

Pro rutinní klinickou praxi je tedy přítomnost opravdu velké nejistoty v oblasti nízkých hodnot zcela nevýznamná. Tím pádem nemá žádný praktický význam, aby se laboratoř určením nejistoty svých výsledků pro takto nízké hodnoty zabývala a měla je připravené pro případ, že „by se na ně někdo zeptal“. Tím se dostáváme k velmi důležitému pravidlu, které se týká odhadů nejistot výsledků měření v klinických laboratořích: Laboratoř by měla znát nejistoty v té oblasti měřicího rozsahu, kam spadá většina (např. 99 %) výsledků všech měření rutinních vzorků, která provádí. A samozřejmě je vhodné zaměřit svou pozornost na dolní i horní konec tohoto intervalu.

Avšak naprosto jiné požadavky mohou mít klinici ve výzkumných, transplantačních a jiných centrech, kde může být např. sledování trendů důležité i u velmi nízkých hodnot. Pokud jsou pro klinika důležité výsledky např. v oblasti < 0,5 x 10⁹/l, pak by se měl skutečně zajímat o nejistotu takových výsledků a po laboratoři ji aktivně požadovat. Je totiž možné, že právě takové hodnoty spadají do výše uvedeného 1 % „neobvyklých“ výsledků, jejichž nejistotu laboratoř vůbec nezkoumala a nezná ji. A tudíž se může stát, že klinik namísto výsledků měření dostává v podstatě náhodná čísla, která nesou vlastně jen jednu pravdivou informaci, a to „počet leukocytů je nízký“. Kolik opravdu je, to už je jiná otázka.

K čemu tedy ty nejistoty vlastně jsou – klinikům

Na straně klinických pracovníků (a obecně všech těch, kteří výsledky měření přijímají a pracují s nimi) je nesmírně důležité:

• Uvědomit si a akceptovat samotnou přítomnost nejistoty v každém výsledku měření. Je důležité nepodlehnout falešné iluzi o „nepřítomnosti nejistoty“ např. u některých POCT (Point of Care Testing) systémů, které výsledky zaokrouhlují na malý počet platných číslic (zpravidla na 2) a při jednoduchém pokusu, kdy je např. 10krát po sobě změřen INR (International Normalized Ratio) jednoho pacienta, opravdu vydají 10 stejných výsledků. Skutečnost je ale taková, že uvnitř přístroj pracuje s větším počtem platných číslic a při opakovaných měřeních INR naměří různé výsledky (např. od 2,78 do 2,84), avšak takto naměřené výsledky pro zobrazení na displeji vždy zaokrouhlí (zde na 2,8). Pokud nemáme o nejistotě žádné informace z dokumentace výrobce a opakovaná měření poskytují konstantní výsledky, pak jediným příspěvkem k celkové nejistotě, s nímž můžeme pracovat, je vliv zaokrouhlování výsledků uvnitř zařízení (před jejich zobrazením). Právě v těchto případech se u digitálních přístrojů obecně mluví o nejistotě „polovina poslední číslice na displeji“, konkrétně u tohoto přístroje bychom tedy nejistotu odhadli jako U_c,abs = 0,05, nebo jako relativní pro výsledek 2,8: U_c,rel = 1,8 %. Další informace – viz bod 2 následující subkapitoly.
• Mít na mysli, že nejistota může hrát naprosto dominantní roli u výsledků, které leží daleko od referenčního intervalu (ať jde o velmi nízké nebo velmi vysoké výsledky). Pokud na absolutní hodnotě takových výsledků skutečně závisí další rozhodování, je na místě dotázat se na nejistotu a zahrnout ji do svých úvah.
• Vzít v úvahu, že nejistota výsledku je vždy závislá na metodě měření – např. „manuální“ metody zpravidla vykazují větší nejistotu než měření na automatickém systému.
• A nezapomenout, že hlavním hráčem na poli nejistot je laboratoř, která by své výstupy pro kliniky měla náležitě opracovat právě s ohledem na nejistoty výsledků měření – viz další odstavec.

K čemu tedy ty nejistoty vlastně jsou – laboratořím

Laboratoř je tím subjektem, který nejistoty svých výsledků zná, ale nikomu je aktivně nesděluje. Odtud se přímo nabízí jednoduchý závěr: Určování nejistot je k ničemu. Pokusme se tomuto závěru oponovat a vybrat alespoň několik případů, kdy laboratoř může znalost nejistoty rozumně prakticky využít při komunikaci se svými zákazníky (nezabýváme se aplikací nejistot „uvnitř“ laboratoře).

1. Typickým příkladem, kde nejistota nachází rozumné uplatnění, je porovnávání výsledků s nějakou hraniční hodnotou, na jehož základě jsou výsledky rozdělovány třeba na „negativní/pozitivní“ nebo „fyziologické/patologické“ apod.
   Uveďme opět reálný příklad, a sice měření počtu retikulocytů a porovnávání výsledků s hranicí referenčního intervalu. Dva účastníci EHK uvedli dramaticky rozdílné nejistoty svých výsledků. Účastník X, který uvedl U_c = 1,8 % říká, že když naměří výsledek 117 x 10⁹/l, pak skutečný počet retikulocytů ve vzorku leží s 95% pravděpodobností v intervalu od 115 do 119 x 10⁹/l. Účastník Y, který uvedl U_c = 45 % říká, že když naměří výsledek 117 x 10⁹/l, pak skutečný počet retikulocytů ve vzorku leží s 95% pravděpodobností v intervalu od 64 do 170 x 10⁹/l. A to je opravdu zásadní rozdíl! Pokud je horní hranice referenčního intervalu pro dospělé 100 x 10⁹/l, pak u prvního účastníka lze jeho výsledek jasně interpretovat tak, že jde o zvýšený počet. Naopak u druhého účastníka nelze říci vůbec nic, jde o zcela neprůkazný výsledek, protože výsledek včetně nejistoty – tj. celá úsečka – neleží nad (nebo pod) danou hranicí. Schematicky tuto situaci popisuje obrázek 6.
   Uvedený příklad pěkně dokumentuje, že i když jsou výsledky numericky naprosto identické, ještě to neznamená, že je můžeme stejně interpretovat, pokud neznáme jejich nejistoty. Pokud výsledek měření zařazujeme do nějaké oblasti (intervalu), pak musí do tohoto intervalu patřit celý, včetně své nejistoty. Obrázek 6 jasně ukazuje, že i kdyby účastník Y naměřil ještě vyšší výsledek, stále by byl neprůkazný, protože jeho nejistota je příliš velká. Také vidíme, že čím je nejistota větší, tím více výsledků „spadne“ do kategorie „neprůkazný výsledek“. Velikost nejistoty tak vlastně vymezuje šíři „šedé zóny“, ve které musí být výsledky hodnoceny jako neprůkazné.
2. Počet platných číslic ve výsledku měření. Občas se nelze zbavit podezření, že některé laboratoře považují za ukazatel kvality výsledku počet číslic, které do něj zapíší. Čím více, tím lépe. Překvapivě v tomto případě neplatí ani opačné rčení „méně je více“. Počet číslic, které má smysl ve výsledku uvádět, lze odvodit právě z velikosti nejistoty a platí pro něj jednouché pravidlo: Nejistotu (absolutní, tj. vyjádřenou v jednotce měření) zaokrouhlíme na jednu platnou číslici a ve stejném řádu vydáme výsledek. Pokud se opět vrátíme k našemu měření počtu leukocytů, pak pro výsledek 5,40 x 10⁹/l máme k dispozici nejistotu U_c,abs = 0,27 x 10⁹/l. Tu zaokrouhlíme na jednu platnou číslici, tedy 0,3 – takto zaokrouhlená nejistota má jedno desetinné místo, a proto naprosto postačuje, pokud výsledek vydáme jako 5,4 x 10⁹/l. Další desetinná místa již představují v podstatě nadbytečný šum, který nepřináší žádnou užitečnou informaci. Velmi podobný princip prezentace výsledků jsme popsali v předchozí subkapitole u POCT systému pro měření INR a zde vidíme, že jde o velice pragmatický postup.
   Je jisté, že adekvátní počet číslic ve výsledku přispívá jednak k čitelnosti a přehlednosti a kromě toho nevzbuzuje zavádějící iluzi ohledně přesnosti daného výsledku.
3. Laboratoř by měla rozumně zvážit své možnosti a nesnažit se o vydávání výsledků, o jejichž nejistotě vůbec nic neví a nespoléhat se jen na to, že z analyzátoru „nějaké číslo vypadlo“. Přidržíme-li se výše uvedeného příkladu hematologického analyzátoru, bylo by jistě na místě, kdyby laboratoř určila hranici, pod kterou již numerický výsledek nevydá a o důvodu informuje klinika formou komentáře. Touto hranicí by měl být právě takový počet leukocytů, kde je nejistota výsledku pro klinickou interpretaci ještě přijatelná.

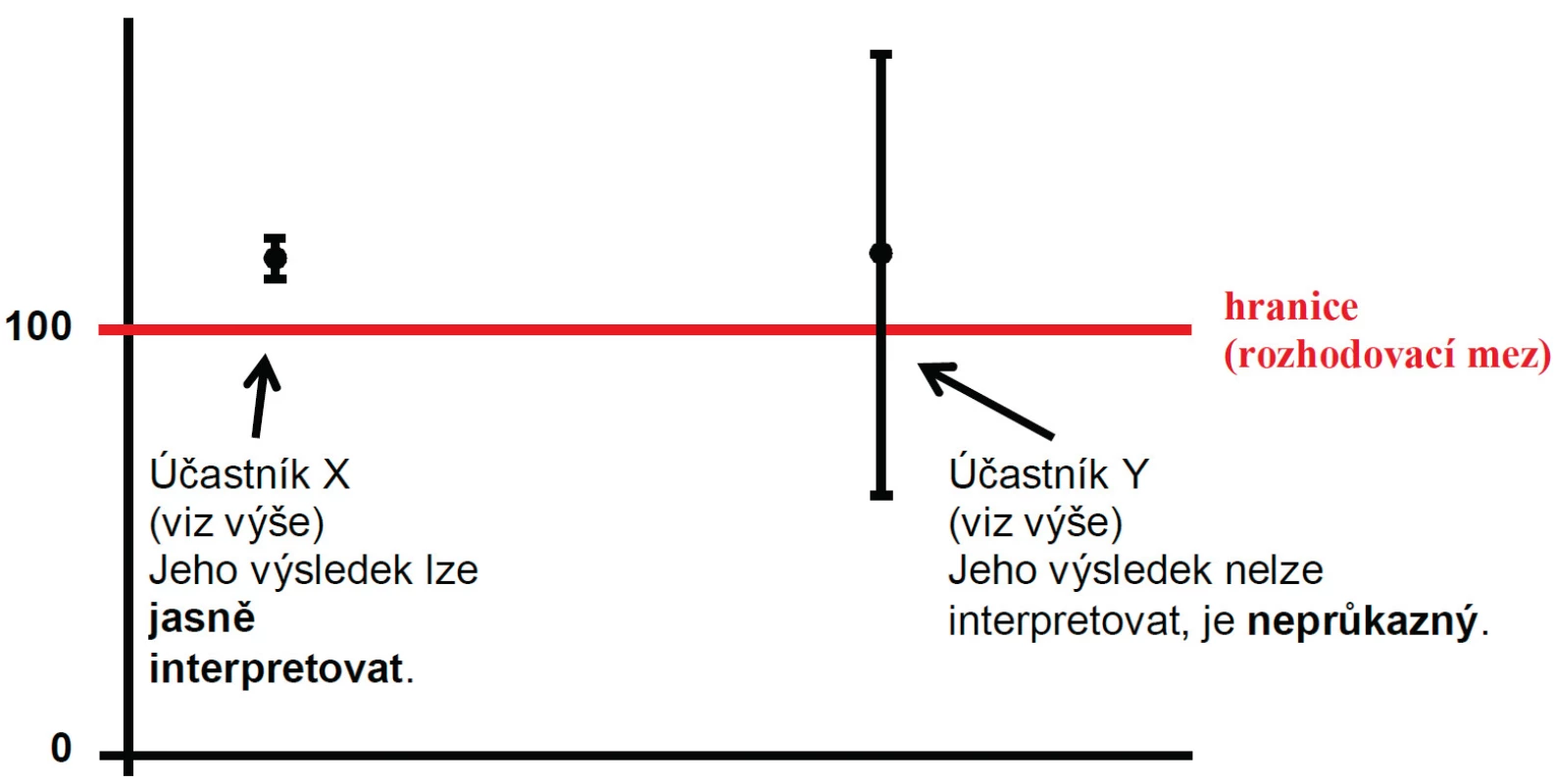
Striktně řečeno, vydávání výsledků, o jejichž nejistotě vůbec nic nevíme, postrádá smysl.

ZÁVĚR

Filozofie nejistot výsledků měření je bezpochyby velice blízká standardnímu modelu uvažování v medicíně, kde se jen málokdy setkáváme s „absolutními pravdami“. Lékař před tím, než určí diagnózu, prakticky vždy zvažuje na základě informací, které má k dispozici, více alternativ a nakonec volí tu nejpravděpodobnější.

Jediné, čím se koncepce nejistot výsledků měření poněkud vymyká výše uvedenému běžnému způsobu uvažování, je to, že vnáší nejistotu i tam, kde by ji možná nikdo nečekal. Nejsme rádi, že výsledky mají nejistotu. Ale představa laboratoře jako technicky dokonalé továrny na naprosto přesná čísla je skutečně chybná a pokud tento text přispěl k pochopení a akceptování této skutečnosti, pak splnil svůj účel.

Čestné prohlášení

Autor sdělení čestně prohlašuje, že v souvislosti s tématem a vznikem tohoto článku není ve střetu zájmů. Rovněž vznik a publikace tohoto článku nebyly podpořeny žádnou farmaceutickou firmou.

Doručeno do redakce dne 16. 2. 2018.

Přijato po recenzi dne 20. 4. 2018.

Ing. Marek Budina

SEKK s.r.o.

Za Pasáží 1609

530 02 Pardubice

e-mail: budina@sekk.cz