-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaDominance of Deleterious Alleles Controls the Response to a Population Bottleneck
Dominance has played a central role in classical genetics since its inception. However, the effect of dominance introduces substantial technical complications into theoretical models describing dynamics of alleles in populations. As a result, dominance is often ignored in population genetic models. Statistical tests for selection built on these models do not discriminate between recessive and additive alleles. We show that historical changes in population size can provide a way to differentiate between recessive and additive selection. Our analysis compares two sub-populations with different demographic histories. History of our own species provides plenty of examples of sub-populations that went through population bottlenecks followed by re-expansions. We show that demographic differences, which generally complicate the analysis, can instead aid in the inference of features of natural selection.
Published in the journal: . PLoS Genet 11(8): e32767. doi:10.1371/journal.pgen.1005436
Category: Research Article
doi: https://doi.org/10.1371/journal.pgen.1005436Summary
Dominance has played a central role in classical genetics since its inception. However, the effect of dominance introduces substantial technical complications into theoretical models describing dynamics of alleles in populations. As a result, dominance is often ignored in population genetic models. Statistical tests for selection built on these models do not discriminate between recessive and additive alleles. We show that historical changes in population size can provide a way to differentiate between recessive and additive selection. Our analysis compares two sub-populations with different demographic histories. History of our own species provides plenty of examples of sub-populations that went through population bottlenecks followed by re-expansions. We show that demographic differences, which generally complicate the analysis, can instead aid in the inference of features of natural selection.
Introduction
In diploid organisms, the fitness effect of an allele, or a group of alleles, can be categorized as additive, dominant or recessive, or as part of a more general epistatic network. A large body of existing work is devoted to the development of statistical methods for the detection and quantification of selection using DNA sequencing data, including comparative genomics and the sequencing of population samples [1–3]. However, much less progress has been made toward developing methods to identify the mode of selection as additive, recessive or dominant. Substantial experimental work in the last 50 years has been devoted to identifying the average dominance coefficient in model organisms, often with disagreement between different studies and techniques [4, 5]. These studies, in an attempt to identify the relationship between dominance coefficients and selective effects, largely focus on mutation accumulation experiments and subsequent laboratory propagation, determining dominance coefficients from the viability of crosses [4, 6]. At least one study attempts to determine the relationship between dominance coefficient and selective effect from natural populations, propagating crosses directly from wild-type samples, however the methodology relies on the often inapplicable assumption of mutation-selection balance [7]. A particularly useful overview of various techniques and studies can be found in [8], with some more modern techniques described in [9]. Additionally, more recent work taking advantage of a large amount of yeast knockout data has made progress towards quantifying the distribution of dominance effects (restricted to the discussion of nonsense mutations), with emphasis on the variance and skew of this distribution [10, 11].
Despite these substantial steps forward, all of the methods employed rely on the ability to rapidly breed laboratory-friendly organisms, either for the purposes of mutation accumulation or production of homozygotes and heterozygotes through crosses. Unfortunately, such techniques are infeasible when dealing with long-lived macroscopic organisms, particularly in the case of humans. In the present work, we hope to provide steps towards the development of techniques applicable to natural populations of such organisms by making use of naturally occurring demographic events and describing the dynamic response of populations to such events.
The genetics of model organisms and of human disease provide plenty of anecdotal evidence in favor of the general importance of dominance [12]. Although genome-wide association studies suggest that alleles of small effects involved in human complex traits frequently act additively, estimation of genetic variance components from large pedigrees suggests a substantial role for dominance in a number of human quantitative traits; LDL cholesterol levels, for example, have a substantial dominance component, as shown in [13]. Alleles of large effects involved in human Mendelian diseases often behave similarly to large effect (and even lethal) spontaneous and induced mutations in model organisms, such as mouse, zebrafish, or flies, that are frequently recessive [4, 14]. In spite of these observations, the role of dominance in population genetic variation and evolution remains largely unexplored in the majority of diploid species and no formal statistical framework is currently available to identify dominance coefficients in natural populations deviating from mutation-selection balance.
A number of theoretical studies suggested that demographic processes associated with the increase in variance of allele frequency distribution result in a more efficient removal of recessive deleterious alleles [15–18]. Such demographic scenarios include population bottlenecks, population subdivision, range expansion, and inbreeding. Increase in the variance of allele frequency distribution during a bottleneck can be characterized by inbreeding coefficient (even in case of a panmictic population). For structured populations, the increase in variance is characterized by FST. Substantial theoretical work and associated experimental studies explored the removal of recessive variants due to increased inbreeding coefficient during sustained population bottlenecks [19–22]. Additionally, several studies note that bottlenecks have a strong effect on nonadditive variation, specifically loci with epistatic interactions [19, 23–30]. To complement these analyses, we focus on genetic variation in panmictic populations that experienced a population bottleneck and subsequent re-expansion, similar to the scenario recently analyzed in [30]. Using a combination of theoretical analysis and computer simulations, we demonstrate that recessive selection can be qualitatively distinguished from additive selection in populations that recently recovered from a temporary bottleneck, and detail the dynamics of the average number of mutations per haploid.
An important study by Kirkpatrick and Jarne [31] qualitatively described how, perhaps counterintuitively, the number of deleterious recessive alleles per haploid genome is transiently reduced after re-expansion following a population bottleneck, while the number of additively or dominantly acting alleles is increased. We focus on this insight and quantitatively extend the analysis of these dynamics to show that, in spite of a well-documented increase in the frequency of some recessively acting variants in founder populations, the average number of deleterious recessive alleles (with dominance coefficient h ≪ 0.5) carried by an individual is reduced as a consequence of the bottleneck. With the growing availability of DNA sequencing data in multiple populations, these results demonstrate the potential to directly evaluate the role of dominance, either on a whole genome level, or in specific categories of genes.
Population bottlenecks are a common feature in the history of many human populations. For example, the “Out of Africa” bottleneck involved the ancestors of many present-day human populations. Numerous recent bottlenecks affected, among others, the well studied populations of Finland and Iceland. More generally, bottlenecks followed by expansions are standard features in the recent evolution of most domesticated organisms, including an analogous “Out of Africa” event in Drosophila melanogaster [32], highlighting the ubiquity of these events in natural populations. We suggest that complex demographic history may assist rather than complicate statistical inference of selection in population genetics.
Here we focus on a comparison between two populations that recently split, after which their demographic histories diverged, one exhibiting a founder’s event (a population bottleneck followed by subsequent re-expansion), and the other maintaining a fixed population size. We analyze their accumulated differences to shed light on the type of selection dominating the dynamics of deleterious alleles, and show that the average number of mutations per individual, 〈x〉, is dependent on the mode of selection characterized by the average dominance coefficient, h. We introduce a measure BR (the “burden ratio” defined below) that is the ratio of per-haploid deleterious allele accumulation in the two populations. This potentially allows for the qualitative distinction between predominantly additive selection (h ≈ 0.5), where mutations accumulate due to relaxed selection during a bottleneck, resulting in BR < 1, and predominantly recessive selection (h ≪ 0.5), where homozygous deleterious mutations are purged from the population after re-expansion from the bottleneck, resulting in BR > 1, as shown in Fig 1.
Fig. 1. Response of the BR statistic for additive and recessive variation. 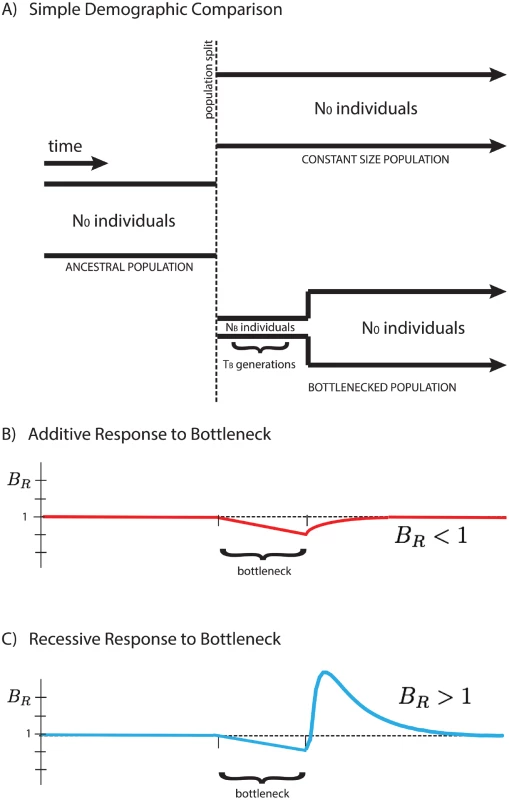
A schematic representation of two populations is presented above (A). Initially a single population prior to the bottleneck event, the populations split and have distinct demographic profiles. The equilibrium population maintains a constant size for easy comparison to the founded population. The latter drastically reduces its population size to NB for a short time TB during the founder’s event. Our statistical comparison between populations B R = 〈 x 〉 e q 〈 x 〉 f o u n d e d is represented here for cases of purely additive (B) and purely recessive (C) variation. The statistic BR > 1 for recessive variation (dominance coefficient h = 0) and BR < 1 for additive variation (h = 1/2), providing a simple indicator for the primary mode of selection of polymorphic alleles in the populations. For qualitative demonstration and development of intuition, the analysis assumes strictly additive and strictly recessive selection with a highly idealized demography. However, this behavior is not restricted to the simplified demographic model presented in this paper, but rather suggests a quite generic qualitative signature for the presence of recessive (or near-recessive) selection in comparison between two populations, one of which experienced a bottleneck event. Additionally, our simulations suggest the potential to distinguish between partially recessive and additive alleles, as the change in the qualitative behavior of BR occurs at intermediate values of the dominance coefficient, h. The temporal dependence of the “critical dominance coefficient”, hc, describing the boundary between BR > 1 and BR < 1, as well as the sensitivity to partial recessivity, is discussed in the S1 Text.
To ask whether the behavior of the BR statistic is consistent with the dynamics of recessive selection in natural populations, we perform a statistical analysis of genes annotated in the literature as causing autosomal recessive (AR) disease. We use the “Out of Africa” event to differentiate between variation in African and European populations, potentially allowing for the identification of recessive selection in natural human populations. We find that sets of AR disease genes show a statistically significant deviation from neutrality, with BR > 1. This suggests that at least some disease-associated genes with autosomal recessive mode of inheritance may be under recessive selection. Although this observation is not surprising, it is nontrivial, as disease genes could be neutral, highly pleiotropic, or contain variants with different modes of inheritance. This analysis demonstrates the potential to use our methodology to identify sets of genes under predominantly recessive selection.
Results
Model
We work with a simple demography described by an ancestral population of N0 individuals that splits into two subpopulations, one with population size N0 equal to the initial population size (“equilibrium”), and one with reduced bottleneck population size NB (“founded”). The latter population persists at this size for TB generations before instantaneously re-expanding to the initial population size N0, as shown in Fig 1. Time t is measured after the re-expansion from the bottleneck, as we are interested in the dynamics during this period. Quantities measured in the equilibrium population, and equivalently prior to the split, are denoted with a subscript “0”. We consider only deleterious mutations with average selective effect of magnitude s > 0, such that s represents the strength of deleterious selection. Extensions of this analysis to a full distribution of selective effects can be found in the S1 Text. The initial population is in a quasi-steady state with 2N0Ud deleterious alleles introduced into the population with a one-way mutation rate Ud per haploid individual per generation and rare fixation of deleterious alleles. In the absence of back-mutations, the population is not strictly in static equilibrium, however, this approximation is reasonable when the back-mutation rate and average derived allele frequencies are relatively low. In approximate equilibrium, the site frequency spectrum (SFS), denoted ϕ(x), for polymorphic alleles is given by Kimura [33].
Here h ≥ 0 is the dominance coefficient for deleterious mutations, where h = 1/2 corresponds to a purely additive set of alleles, and h = 0 corresponds to the purely recessive case. For the present analysis, we primarily focus on these two limits, contrasting their effects on the genetic diversity. An expanded discussion of the treatment of intermediate dominance coefficients can be found in the S1 Text. The solution represents a mutation-selection-drift balance in which new mutations are exactly compensated for by the purging of currently polymorphic alleles by both selection and extinction due to stochastic drift. In this way, an approximately static number of polymorphic alleles exists in the population at any given time.
Population dynamics
As noted above, a qualitative insight on the effect of the bottleneck on recessive variation was previously obtained by noting that the expected change in frequency of recessive allele is accelerated due to the increased variance of allele frequencies (inbreeding coefficient). We offer a different approach and attempt to quantitatively describe the difference in dynamics between additive and recessive variation.
We follow the expected number of mutations per chromosome in the population, noting that it is simply the first moment of SFS.
When multiplied by s, this is the effective “mutation load” of each individual in the additive case, but in the case of purely recessive selection this is not proportional to the fitness, as selection acts only on homozygotes. We refer to this statistic generally as the “mutation burden” to avoid assumption of any given mode of selection. As described below, comparison between the mutation burden in the equilibrium and founded populations in the form of the “burden ratio”, BR, may prove useful in the identification of sets of alleles under recessive selection.
To gain intuition for this qualitative difference, we work to quantitatively understand the population dynamics in a simple demography, first for purely additive selection, and then for purely recessive selection for comparison.
Additive selection and response to a bottleneck
The initial site frequency spectrum ϕ0A(x) for purely additive alleles is given by Eq (1) with h = 1/2.
Here θ0 = 4N0Ud. In the deterministic limit, when 2N0s ≫ 1, the SFS rapidly decays as x → 1 simplifying the functional form [34]. We approximately compute the initial mutation burden as follows.
This describes the deterministic mutation-selection balance for mutations under strong selection. Now we deviate from equilibrium by reducing the population size to 2NB chromosomes, representing a population bottleneck. The effect that a bottleneck has on the site frequency spectrum is twofold: a fraction of alleles are removed from the population due to increased random drift, and the mean of the remaining alleles occurs at higher frequency. The dynamics of the distribution ϕ(x, t) during such a change in demography can be computed from Kolmogorov’s forward equation, as detailed in the S1 Text. The first moment of the distribution, the mutation burden, follows the temporal dynamics derived from summing the Kolmogorov equation over all alleles in the genome, and takes the following form.
As discussed in [35, 36], the burden of additive mutations is not directly affected by drift, as the drift term vanishes from the dynamics of the first moment, however the dependence on the second moment introduces an indirect dependence on drift. In the strong selection regime, in the limit where 〈x2〉 ≪ 〈x〉, extinction of some alleles is exactly compensated for by an increase in the frequency of other alleles. This is true in the equilibrium distribution prior to the bottleneck when N0s ≫ 1, where 〈x〉0∼O(Ud/s) and 〈x02〉∼
Zdroje
1. Eyre-Walker A and Keightley PD (2007) The distribution of fitness effects of new mutations. Nat. Rev. Genet. 8 : 610–618. doi: 10.1038/nrg2146 17637733
2. Sella G, et. al. (2009) Pervasive Natural Selection in the Drosophila Genome? PLoS Genet 5: e1000495. doi: 10.1371/journal.pgen.1000495 19503600
3. Cutter AD and Payseur BA (2013) Genomic signatures of selection at linked sites: unifying the disparity among species. Nat. Rev. Genet. 14 : 262–74. doi: 10.1038/nrg3425 23478346
4. Mukai T (1972) Mutation rate and dominance of genes affecting viability in Drosophila Melanogaster. Genetics 72 : 335–355. 4630587
5. Garcia-Dorado A and Caballero A (2000) On the average coefficient of dominance of deleterious spontaneous mutations. Genetics 155 : 1991–2001. 10924491
6. Simmons MJ and Crow JF (1977) Mutations affecting fitness in Drosophila populations. Ann. Rev. Genet. 11 : 49–78. doi: 10.1146/annurev.ge.11.120177.000405 413473
7. Deng HW and Lynch M (1996) Estimation of deleterious-mutation parameters in natural populations. Genetics 144 : 349–360. 8878698
8. Garcia-Dorado A, Lopez-Fanzul C and Caballero A (1999) Properties of spontaneous mutations affecting quantitative traits. Genet. Res. 74 : 341–350. doi: 10.1017/S0016672399004206 10689810
9. Manna F, Martin G, and Lenormand T (2011) Fitness landscapes: An alternative theory for the dominance of mutation. Genetics 189 : 923–937. doi: 10.1534/genetics.111.132944 21890744
10. Phadnis N and Fry JD (2005) Widespread correlations between dominance and homozygous effects of mutations: Implications for theories of dominance. Genetics 171 : 385–392. doi: 10.1534/genetics.104.039016 15972465
11. Agrawal AF and Whitlock MC (2011) Inferences about the distribution of dominance drawn from yeast gene knockout data. Genetics 187 : 553–566. doi: 10.1534/genetics.110.124560 21098719
12. Lynch M and Walsh B (1998) Genetics and analysis of quantitative traits. Sinauer Assocs., Inc., Sunderland, MA.
13. Newman DL, et al. (2001) The importance of genealogy in determining genetic associations with complex traits. Am. J. Hum. Genet. 69 : 1146–1148. doi: 10.1086/323659 11590549
14. Herron BJ, et al. (2002) Efficient generation and mapping of recessive developmental mutations using ENU mutagenesis. Nat. Genet. 30 : 185–189. doi: 10.1038/ng812 11818962
15. Wang J, et al. (1999) Dynamics of inbreeding depression due to deleterious mutations in small populations: mutation parameters and inbreeding rate. Genet. Res. 74 : 165–178. doi: 10.1017/S0016672399003900 10584559
16. Whitlock MC (2002) Selection, load and inbreeding depression in a large metapopulation. Genetics 160 : 1191–1202. 11901133
17. Garcia-Dorado A (2008) A simple method to account for natural selection when predicting inbreeding depression. Genetics 180 : 1559–1566. doi: 10.1534/genetics.108.090597 18791247
18. Peischl S and Excoffier L (2015) Expansion load: recessive mutations and the role of standing genetic variation. Molecular Ecology 24 : 2084–2094. doi: 10.1111/mec.13154 25786336
19. Robertson A (1952) The effect of inbreeding on the variation due to recessive genes. Genetics 37 : 189–207. 17247385
20. Bryant EH, McCommas SA, and Combs LM (1986) The effect of an experimental bottleneck upon quantitative genetic-variation in the housefly. Genetics 114 : 1191–1211. 17246359
21. Wang JL, et. al. (1998) Bottleneck effect on genetic variance: A theoretical investigation of the role of dominance. Genetics 150 : 435–447, 1998. 9725859
22. Zhang XS, Wang J, and Hill WG (2004) Redistribution of gene frequency and changes of genetic variation following a bottleneck in population size. Genetics 167 : 1475–1492. doi: 10.1534/genetics.103.025874 15280256
23. Goodnight CJ (1987) On the effect of founder events on the epistatic genetic variance. Evolution 41 : 80–91. doi: 10.2307/2408974
24. Goodnight CJ (1988) Epistasis and the effect of founder events on the additive genetic variance. Evolution 42 : 441–454. doi: 10.2307/2409030
25. Cheverud JM and Routman EJ (1996) Epistasis as a source of increased additive genetic variance at population bottlenecks. Evolution 50 : 1042–1051. doi: 10.2307/2410645
26. Hill WG, Caballero A, and Wang J (1998) The effect of linkage disequilibrium and deviation from Hardy-Weinberg proportions on the changes in genetic variance with bottlenecking. Heredity 81 : 174–186. doi: 10.1046/j.1365-2540.1998.00390.x
27. Naciri-Graven Y and Goudet J (2003) The additive genetic variance after bottlenecks is affected by the number of loci involved in epistatic interactions. Evolution 57 : 706–716. doi: 10.1554/0014-3820(2003)057%5B0706:TAGVAB%5D2.0.CO;2 12778542
28. Barton NH and Turelli M (2004) Effects of genetic drift on variance components under a general model of epistasis. Evolution 58 : 2111–2132. doi: 10.1554/03-684 15562679
29. Hill WG, Barton NH, and Turelli M (2006) Prediction of effects of genetic drift on variance components under a general model of epistasis. Theor. Popul. Biol. 70 : 56–62. doi: 10.1016/j.tpb.2005.10.001 16360188
30. Turelli M and Barton NH (2006) Will population bottlenecks and multilocus epistasis increase additive genetic variance? Evolution 60 : 1763–1776. doi: 10.1111/j.0014-3820.2006.tb00521.x 17089962
31. Kirkpatrick M and Jarne P (2000) The effects of a bottleneck on inbreeding depression and the genetic load. Am. Nat. 155(2):154–167. doi: 10.1086/303312 10686158
32. Lachaise D, et al. (2004) Nine relatives from one African ancestor: population biology and evolution of the Drosophila melanogaster subgroup species. In: Singh RS and Uyenoyama MK (eds.) The Evolution of Population Biology. pp. 315–344. [Online]. Cambridge: Cambridge University Press.
33. Kimura M (1964) Diffusion models in population genetics. J. Ap. Prob. 1 : 177–232. doi: 10.2307/3211856
34. Nei M (1968) The frequency distribution of lethal chromosomes in finite populations. Proc. Natl. Acad. Sci. USA 60 : 517–524. doi: 10.1073/pnas.60.2.517 5248809
35. Simons YB, Turchin MC, Pritchard JK, and Sella G (2014) The deleterious mutation load is insensitive to recent population history. Nat. Gen. 46, 220–224. doi: 10.1038/ng.2896
36. Do R, et al. (2015) No evidence that selection has been less effective at removing deleterious mutations in Europeans than in Africans. Nat. Gen. 47 : 126–131. doi: 10.1038/ng.3186
37. Fu W, et al. (2013) Analysis of 6,515 exomes reveals the recent origin of most human protein-coding variants. Nature 493 : 216–20. doi: 10.1038/nature11690 23201682
38. Stenson PD, et al. (2009) The Human Gene Mutation Database: providing a comprehensive central mutation database for molecular diagnostics and personalized genomics. Hum Genomics 4(2):69–72. doi: 10.1186/1479-7364-4-2-69 20038494
39. Partners Center for Personalized Genetic Medicine, Brigham and Women’s Hospital (2014) Laboratory for Molecular Medicine Tests. Available: http://personalizedmedicine.partners.org/laboratory-for-molecular-medicine/tests/default.aspx. Accessed 1 July 2014.
40. Solomon BD, Nguyen A, Bear KA and Wolfsberg TG (2013) Clinical Genomic Database. Proc. Natl. Acad. Sci. USA 110(24):9851–9855. doi: 10.1073/pnas.1302575110 23696674
41. The 1000 Genomes Project Consortium (2012) An integrated map of genetic variation from 1,092 human genomes. Nature 491(7422):56–65. doi: 10.1038/nature11632 23128226
42. Slatkin M (2004) A population-genetic test of founder effects and implications for Ashkenazi Jewish diseases. Am. J. Hum. Genet. 75 : 282–293. doi: 10.1086/423146 15208782
43. Gazave E, Chang D, Clark AG, and Keinan A (2013) Population growth inflates the per-individual number of deleterious mutations and reduces their mean effect. Genetics 195(3):969–78. doi: 10.1534/genetics.113.153973 23979573
44. Peischl S, Dupanloup I, Kirkpatrick M, and Excoffier L (2013) On the accumulation of deleterious mutations during range expansions. Mol. Ecol. 22 : 5972–5982. doi: 10.1111/mec.12524 24102784
45. Keinan A, Mullikin JC, Patterson N, and Reich D (2007) Measurement of the human allele frequency spectrum demonstrates greater genetic drift in East Asians than in Europeans. Nat. Genet. 39 : 1251–1255. doi: 10.1038/ng2116 17828266
46. Lohmueller KE, et al. (2008) Proportionally more deleterious genetic variation in European than in African populations. Nature 451(7181):994–997. doi: 10.1038/nature06611 18288194
47. Gravel S, et al. (2011) Demographic history and rare allele sharing among human populations. Proc. Natl. Acad. Sci. USA 108 : 11983–11988. doi: 10.1073/pnas.1019276108 21730125
48. Tennessen JA, et al. (2012) Evolution and functional impact of rare coding variation from deep sequencing of human exomes. Science 337(6090):64–69. doi: 10.1126/science.1219240 22604720
49. Gronau I
et al. (2011) Bayesian inference of ancient human demography from individual genome sequences. Nat. Genet. 43 : 1031–1034. doi: 10.1038/ng.937 21926973
50. Li H and Durbin R (2012) Inference of human population history from whole genome sequence of a single individual. Nature 475 : 493–496. doi: 10.1038/nature10231
51. Sheehan S, Harris K, and Song YS (2013) Estimating variable effective population sizes from multiple genomes: a sequentially markov conditional sampling distribution approach. Genetics 194 : 647–62. doi: 10.1534/genetics.112.149096 23608192
52. Harris K and Nielsen R (2013) Inferring demographic history from a spectrum of shared haplotype lengths. PLoS Genet. 9:e1003521. doi: 10.1371/journal.pgen.1003521 23754952
53. Macleod IM, et al. (2013) Inferring demography from runs of homozygosity in whole-genome sequence, with correction for sequence errors. Mol. Biol. Evol. 30 : 2209–2223. doi: 10.1093/molbev/mst125 23842528
54. Lohmueller KE (2014) The Impact of Population Demography and Selection on the Genetic Architecture of Complex Traits. PLoS Genet. 10(5):e10004379. doi: 10.1371/journal.pgen.1004379
Štítky
Genetika Reprodukční medicína
Článek Loss and Gain of Natural Killer Cell Receptor Function in an African Hunter-Gatherer PopulationČlánek Let-7 Represses Carcinogenesis and a Stem Cell Phenotype in the Intestine via Regulation of Hmga2Článek Binding of Multiple Rap1 Proteins Stimulates Chromosome Breakage Induction during DNA ReplicationČlánek SLIRP Regulates the Rate of Mitochondrial Protein Synthesis and Protects LRPPRC from DegradationČlánek Protein Composition of Infectious Spores Reveals Novel Sexual Development and Germination Factors inČlánek The Formin Diaphanous Regulates Myoblast Fusion through Actin Polymerization and Arp2/3 RegulationČlánek Runx1 Transcription Factor Is Required for Myoblasts Proliferation during Muscle Regeneration
Článek vyšel v časopisePLOS Genetics
Nejčtenější tento týden
2015 Číslo 8- Akutní intermitentní porfyrie
- Souvislost haplotypu M2 genu pro annexin A5 s opakovanými reprodukčními ztrátami
- Primární hyperoxalurie – aktuální možnosti diagnostiky a léčby
- Doc. Miloš Kubánek: Nemocní se srdeční amyloidózou jsou často skryti a sledováni pod jinými diagnózami
- Transthyretinová amyloidóza z pohledu neurologa a kardiologa aneb jak se vyhnout „misdiagnostice“?
-
Všechny články tohoto čísla
- Putting the Brakes on Huntington Disease in a Mouse Experimental Model
- Identification of Driving Fusion Genes and Genomic Landscape of Medullary Thyroid Cancer
- Evidence for Retromutagenesis as a Mechanism for Adaptive Mutation in
- TSPO, a Mitochondrial Outer Membrane Protein, Controls Ethanol-Related Behaviors in
- Evidence for Lysosome Depletion and Impaired Autophagic Clearance in Hereditary Spastic Paraplegia Type SPG11
- Loss and Gain of Natural Killer Cell Receptor Function in an African Hunter-Gatherer Population
- Trans-Reactivation: A New Epigenetic Phenomenon Underlying Transcriptional Reactivation of Silenced Genes
- Early Developmental and Evolutionary Origins of Gene Body DNA Methylation Patterns in Mammalian Placentas
- Strong Selective Sweeps on the X Chromosome in the Human-Chimpanzee Ancestor Explain Its Low Divergence
- Dominance of Deleterious Alleles Controls the Response to a Population Bottleneck
- Transient 1a Induction Defines the Wound Epidermis during Zebrafish Fin Regeneration
- Systems Genetics Reveals the Functional Context of PCOS Loci and Identifies Genetic and Molecular Mechanisms of Disease Heterogeneity
- A Genome Scale Screen for Mutants with Delayed Exit from Mitosis: Ire1-Independent Induction of Autophagy Integrates ER Homeostasis into Mitotic Lifespan
- Non-synonymous FGD3 Variant as Positional Candidate for Disproportional Tall Stature Accounting for a Carcass Weight QTL () and Skeletal Dysplasia in Japanese Black Cattle
- The Relationship between Gene Network Structure and Expression Variation among Individuals and Species
- Calmodulin Methyltransferase Is Required for Growth, Muscle Strength, Somatosensory Development and Brain Function
- The Wnt Frizzled Receptor MOM-5 Regulates the UNC-5 Netrin Receptor through Small GTPase-Dependent Signaling to Determine the Polarity of Migrating Cells
- Nbs1 ChIP-Seq Identifies Off-Target DNA Double-Strand Breaks Induced by AID in Activated Splenic B Cells
- CCNYL1, but Not CCNY, Cooperates with CDK16 to Regulate Spermatogenesis in Mouse
- Evidence for a Common Origin of Blacksmiths and Cultivators in the Ethiopian Ari within the Last 4500 Years: Lessons for Clustering-Based Inference
- Of Fighting Flies, Mice, and Men: Are Some of the Molecular and Neuronal Mechanisms of Aggression Universal in the Animal Kingdom?
- Hypoxia and Temperature Regulated Morphogenesis in
- The Homeodomain Iroquois Proteins Control Cell Cycle Progression and Regulate the Size of Developmental Fields
- Evolution and Design Governing Signal Precision and Amplification in a Bacterial Chemosensory Pathway
- Rac1 Regulates Endometrial Secretory Function to Control Placental Development
- Let-7 Represses Carcinogenesis and a Stem Cell Phenotype in the Intestine via Regulation of Hmga2
- Functions as a Positive Regulator of Growth and Metabolism in
- The Nucleosome Acidic Patch Regulates the H2B K123 Monoubiquitylation Cascade and Transcription Elongation in
- Rhoptry Proteins ROP5 and ROP18 Are Major Murine Virulence Factors in Genetically Divergent South American Strains of
- Exon 7 Contributes to the Stable Localization of Xist RNA on the Inactive X-Chromosome
- Regulates Refractive Error and Myopia Development in Mice and Humans
- mTORC1 Prevents Preosteoblast Differentiation through the Notch Signaling Pathway
- Regulation of Gene Expression Patterns in Mosquito Reproduction
- Molecular Basis of Gene-Gene Interaction: Cyclic Cross-Regulation of Gene Expression and Post-GWAS Gene-Gene Interaction Involved in Atrial Fibrillation
- The Spalt Transcription Factors Generate the Transcriptional Landscape of the Wing Pouch Central Region
- Binding of Multiple Rap1 Proteins Stimulates Chromosome Breakage Induction during DNA Replication
- Functional Divergence in the Role of N-Linked Glycosylation in Smoothened Signaling
- YAP1 Exerts Its Transcriptional Control via TEAD-Mediated Activation of Enhancers
- Coordinated Evolution of Influenza A Surface Proteins
- The Evolutionary Potential of Phenotypic Mutations
- Genome-Wide Association and Trans-ethnic Meta-Analysis for Advanced Diabetic Kidney Disease: Family Investigation of Nephropathy and Diabetes (FIND)
- New Routes to Phylogeography: A Bayesian Structured Coalescent Approximation
- SLIRP Regulates the Rate of Mitochondrial Protein Synthesis and Protects LRPPRC from Degradation
- Satellite DNA Modulates Gene Expression in the Beetle after Heat Stress
- SHOEBOX Modulates Root Meristem Size in Rice through Dose-Dependent Effects of Gibberellins on Cell Elongation and Proliferation
- Reduced Crossover Interference and Increased ZMM-Independent Recombination in the Absence of Tel1/ATM
- Suppression of Somatic Expansion Delays the Onset of Pathophysiology in a Mouse Model of Huntington’s Disease
- Protein Composition of Infectious Spores Reveals Novel Sexual Development and Germination Factors in
- The Evolutionarily Conserved LIM Homeodomain Protein LIM-4/LHX6 Specifies the Terminal Identity of a Cholinergic and Peptidergic . Sensory/Inter/Motor Neuron-Type
- SmD1 Modulates the miRNA Pathway Independently of Its Pre-mRNA Splicing Function
- piRNAs Are Associated with Diverse Transgenerational Effects on Gene and Transposon Expression in a Hybrid Dysgenic Syndrome of .
- Retinoic Acid Signaling Regulates Differential Expression of the Tandemly-Duplicated Long Wavelength-Sensitive Cone Opsin Genes in Zebrafish
- The Formin Diaphanous Regulates Myoblast Fusion through Actin Polymerization and Arp2/3 Regulation
- Genome-Wide Analysis of PAPS1-Dependent Polyadenylation Identifies Novel Roles for Functionally Specialized Poly(A) Polymerases in
- Runx1 Transcription Factor Is Required for Myoblasts Proliferation during Muscle Regeneration
- Regulation of Mutagenic DNA Polymerase V Activation in Space and Time
- Variability of Gene Expression Identifies Transcriptional Regulators of Early Human Embryonic Development
- The Drosophila Gene Interacts Genetically with and Shows Female-Specific Effects of Divergence
- Functional Activation of the Flagellar Type III Secretion Export Apparatus
- Retrohoming of a Mobile Group II Intron in Human Cells Suggests How Eukaryotes Limit Group II Intron Proliferation
- PLOS Genetics
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Exon 7 Contributes to the Stable Localization of Xist RNA on the Inactive X-Chromosome
- YAP1 Exerts Its Transcriptional Control via TEAD-Mediated Activation of Enhancers
- SmD1 Modulates the miRNA Pathway Independently of Its Pre-mRNA Splicing Function
- Molecular Basis of Gene-Gene Interaction: Cyclic Cross-Regulation of Gene Expression and Post-GWAS Gene-Gene Interaction Involved in Atrial Fibrillation
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání









