-
Články
- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Analýza dat v neurologii LXXI.<br>Pearsonův korelační koeficient
Autoři: L. Dušek; T. Pavlík; Jiří Jarkovský
; J. Koptíková
Působiště autorů: Institut biostatistiky a analýz, LF MU, Brno
Vyšlo v časopise: Cesk Slov Neurol N 2018; 81(5): 608-613
Kategorie: Okénko statistika
V sérii výukových článků tento rok řešíme hodnocení vztahu dvou spojitých proměnných. Výklad jsme započali analýzou lineárního vztahu mezi dvěma spojitými, normálně rozloženými veličinami a minulé dva díly jsme věnovali vysvětlení pojmu kovariance značené cov(X, Y). Kovariance je jedním ze základních ukazatelů síly vztahu dvou proměnných. U normálně rozložených veličin pracujeme s aritmetickým průměrem a rozptylem a z těchto statistických ukazatelů středu a variability rozložení vychází také vztah pro výpočet kovariance:
xi, yi jsou jednotlivé hodnoty proměnných X a Y naměřené párově u i = 1 až i = N jedinců v analyzovaném souboru,
x– , y– jsou aritmetické průměry proměnných X a Y.
Připomeňme, že kovariance je ukazatelem síly lineárního vztahu dvou proměnných, přičemž její kladná hodnota značí vztah pozitivní a záporná hodnota vztah negativní. Kovariance blízká nule dokládá neexistenci vztahu, kdy hodnoty obou proměnných na sobě nijak nezávisí a vyskytují se v pozici vůči svým průměrným hodnotám zcela náhodně.
V minulém díle jsme rovněž rozebírali největší nevýhodu kovariance, a to že její hodnoty závisí na rozptylu obou proměnných, resp. na jednotkách, ve kterých jsou vyjadřovány. Pro odhad kovariance tedy není definována maximální hodnota, která by vyjadřovala nejsilnější možný vztah zkoumaných proměnných (jejich hodnoty by v takovém případě ležely přesně na přímce). To značně omezuje interpretaci odhadu kovariance a snižuje srovnatelnost odhadů kovariance z různých studií. Proto bývá kovariance často citována jako nestandardizovaný ukazatel síly vztahu proměnných.
Výše uvedená nevýhoda kovariance je také důvodem, proč je pro vyjádření síly či „těsnosti“ vztahu dvou spojitých proměnných běžně využíván jiný ukazatel, tzv. Pearsonův korelační koeficient (Pearson’s correlation coefficient), někdy také označovaný jako párový korelační koeficient. Označuje se R, r, R(X, Y) nebo rxy. V praxi se běžně vynechává označení Pearsonův a používá se pouze označení korelační koeficient. Korelační koeficient odhadnutý na výběrovém vzorku N subjektů je označován jako výběrový korelační koeficient. Jeho cílová populační hodnota je typicky značena řeckým písmenem ρ.
Korelační koeficient je na rozdíl od kovariance statistikou standardizovanou, což pochopíme ze vztahu pro jeho výpočet:
Je zřejmé, že vztah vychází z výpočtu kovariance, u kterého ve jmenovateli zlomku přibyly hodnoty směrodatných odchylek obou proměnných sx a sy. Tímto přestala být výsledná hodnota R závislá na jednotkách či rozptylu proměnných a může nabývat pouze hodnot v intervalu od – 1 do + 1. Dělení směrodatnou odchylkou standardizuje u normálního rozdělení vzdálenost hodnoty xi od průměru veličiny X. Získáváme tak z skóre, např. pro proměnnou X:
Hodnoty R blízké nule značí neexistující lineární vztah obou proměnných, hodnoty záporné ukazují na záporný lineární vztah a naopak kladné hodnoty koeficientu ukazují na vztah kladný. Doplníme-li do výše uvedeného vztahu vzorce pro směrodatné odchylky, získáme pro výpočet R následující formu zápisu:
Obecnější formou zápisu je následující vztah, kde E a D jsou označením výpočtu střední hodnoty a rozptylu:
Vlastní výpočet korelačního koeficientu dokládá příklad 1. Jde o bodový odhad hodnoty korelačního koeficientu na daném výběru hodnot o velikosti N = 6. Tento výběrový korelační koeficient je možné, tak jako u jiných výběrových statistik, doplnit 100(1 – α)% intervalem spolehlivosti (confidence interval), přičemž nejčastěji bývá publikován 95% interval. Postup výpočtu přibližujeme v příkladu 2, ze kterého je patrné, že výpočet zahrnuje poměrně složitou tzv. Fisherovu transformaci. Ačkoli totiž korelační koeficient vyžaduje splnění předpokladu normality vstupních proměnných X a Y, hodnoty korelačního koeficientu nemají normální rozdělení. Proto je nutné aplikovat normalizující transformaci, která převádí hodnotu R na z skóre.
Příklad 1. Výpočet výběrového Pearsonova korelačního koeficientu. 
Tab. 1. Příklad 2. Výpočet intervalu spolehlivosti výběrového Pearsonova korelačního koeficientu. 
Příklad 2 – pokračování. Výpočet intervalu spolehlivosti výběrového Pearsonova korelačního koeficientu 
Tab. 2. Příklad 3. Testování statistické významnosti Pearsonova korelačního koeficientu na hladině α = 0,05. 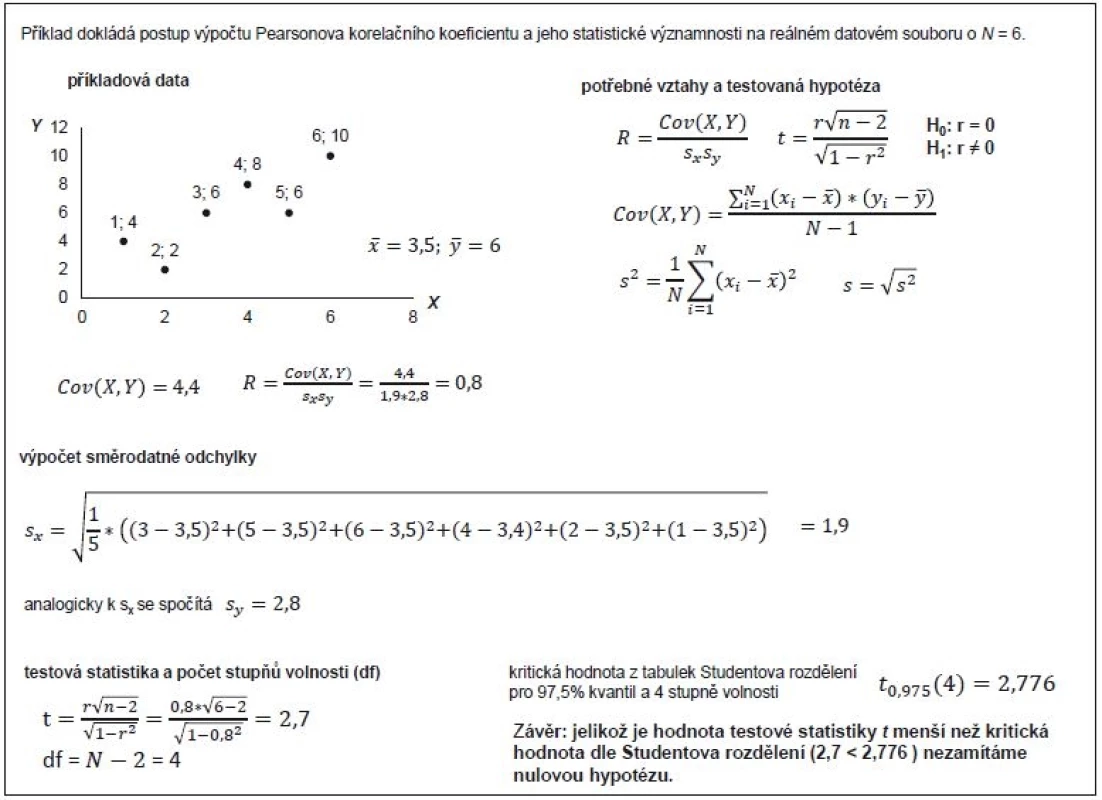
Příklad 4. Výpočet Pearsonova korelačního koefi cientu, jeho intervalu spolehlivosti a statistické významnosti. 
Interpretace intervalu spolehlivosti pro korelační koeficient se nijak neliší od interpretace pro jakýkoli jiný statistický ukazatel. Tedy např. 95% interval spolehlivosti udává dolní a horní hranici pro hodnoty R, v rámci kterých by se vyskytlo 95 výběrových odhadů R, pokud bychom odhad 100× nezávisle opakovali. Z hlediska interpretace intervalu spolehlivosti je dále zásadní pozice nuly. Pokud interval spolehlivosti korelačního koeficientu zahrnuje hodnotu nula, nelze tento koeficient označit za významně odlišný od nuly, a tedy nelze potvrdit existenci lineárního vztahu mezi oběma proměnnými.
Samotný interval spolehlivosti by ovšem neměl nahrazovat klasické statistické testy o významnosti korelačního koeficientu. Statistickou významností R myslíme situaci, kdy je hodnota R statisticky prokazatelně rozdílná od nuly. Testujeme tedy platnost nulové hypotézy R = 0, a pokud tu zamítneme pomocí výpočtu testové statistiky, pak platí R ≠ 0 a mezi oběma veličinami existuje prokazatelný (statisticky významný) lineární vztah. Pro testy týkající se významnosti korelačního koeficientu používáme testovou statistiku Studentova rozdělení (t) s N – 2 stupni volnosti. Příklad 3 dokumentuje výpočet tohoto statistického testu s výsledkem, který nevedl k zamítnutí nulové hypotézy. Příklad 4 naopak uceleně shrnuje hodnocení odhadu korelace dvou proměnných, která je vysoce statisticky významná. Na tyto příklady navazuje příklad 5, který ukazuje tři kvalitativně rozdílné výsledky korelační analýzy, vč. kalkulovaných 95% intervalů spolehlivosti pro odhad R a provedených testů statistické významnosti R.
Stejně jako v případě kovariance i u korelační analýzy vzniká v praxi často potřeba vyhodnotit současně korelaci více než dvou proměnných. Při současném zpracování K proměnných hodnotíme korelaci pro K*(K – 1)/2 dvojic, které sestavujeme do tzv. korelační matice, jejíž řádky a sloupce jsou věnovány postupně první až K-té proměnné. Na průsečíku i-tého řádku a j-tého sloupce je uvedena korelace i-té a j-té proměnné. Korelační matice je čtvercová (symetrická podle hlavní diagonály) a na diagonále obsahuje korelační koeficienty rovny jedné, neboť platí, že R(X, X) = 1. Příklad 6 dokumentuje grafické znázornění korelační matice, které se nazývá korelogram.
Příklad 5. Pearsonův korelační koeficient a jeho statistická významnost. 
Příklad 6. Korelační matice a korelogram. 
Na závěr tohoto dílu uvádíme několik poznámek, které sice z výše uvedeného výkladu vyplývají, ale měly by být pro svůj význam zdůrazněny:
Pearsonův korelační koeficient má smysl hodnotit pouze u lineárních (přímkových) vztahů proměnných X a Y. Pro nelineární vztahy nemá výpočet této korelace žádný smysl.
Výpočet Pearsonova korelačního koeficientu vyžaduje normální rozdělení obou korelovaných proměnných. Významné odchylky od normálního rozdělení, zešikmení rozdělení či výskyt odlehlých hodnot, vážným způsobem zkreslují hodnotu korelačního koeficientu a znehodnocují jeho výpočet. Ověření předpokladu normality rozdělení proměnných vstupujících do korelační analýzy je naprostou nutností.
Test statistické významnosti ověřuje platnost nulové hypotézy R = 0 a v případě jejího zamítnutí prokazujeme statisticky významný lineární vztah dvou proměnných. Nic více, nejde o průkaz kauzality vztahu či příčinné závislosti.
A naopak pokud potvrdíme platnost nulové hypotézy R = 0, znamená to, že mezi proměnnými neexistuje prokazatelný lineární vztah. Může však mezi nimi být jiná forma nelineární závislosti. Nekorelovanost neznamená nezávislost.
Test ověřující platnost hypotézy R = 0 je oboustranný. Pokud to daná analýza vyžaduje, můžeme ověřovat i hypotézy jednostranné, jako např. R < 0 nebo R > 0.
doc. RNDr. Ladislav Dušek, Ph.D.
Institut biostatistiky a analýz, LF MU, Brno
e‑mail: dusek@iba.muni.cz
Štítky
Dětská neurologie Neurochirurgie Neurologie
Článek Nejlepší postup v terapii motoricky pokročilé Parkinsonovy nemoci je INTRADUODENÁLNÍ LEVODOPAČlánek Najlepší postup v terapii motoricky pokročilej Parkinsonovej nemoci je HLBOKÁ MOZGOVÁ STIMULÁCIAČlánek Vztah mezi epidemiologií a subjektivním vnímáním bolesti u pacientů se syndromem karpálního tuneluČlánek Recenze knih
Článek vyšel v časopiseČeská a slovenská neurologie a neurochirurgie
Nejčtenější tento týden
2018 Číslo 5- Metamizol jako analgetikum první volby: kdy, pro koho, jak a proč?
- Moje zkušenosti s Magnosolvem podávaným pacientům jako profylaxe migrény a u pacientů s diagnostikovanou spazmofilní tetanií i při normomagnezémii - MUDr. Dana Pecharová, neurolog
- Magnosolv a jeho využití v neurologii
- Nejčastější nežádoucí účinky venlafaxinu během terapie odeznívají
-
Všechny články tohoto čísla
- Anestezie a nervosvalová onemocnění
- Nejlepší postup v terapii motoricky pokročilé Parkinsonovy nemoci je INTRADUODENÁLNÍ LEVODOPA
- Nejlepší postup v terapii motoricky pokročilé Parkinsonovy nemoci je APOMORFINOVÁ INFUZE
- Najlepší postup v terapii motoricky pokročilej Parkinsonovej nemoci je HLBOKÁ MOZGOVÁ STIMULÁCIA
- Nejlepší postup v terapii motoricky pokročilé Parkinsonovy nemoci je intraduodenální levodopa, apomorfi nová infuze nebo DBS?
- Cervikální vertigo – fikce či realita?
-
Cervikální vertigo – fikce či realita?
Komentář k článku Z. Kadaňky Jr. et al - Péče o pacienty s dysfagií po cévní mozkové příhodě v České republice
- Matematické modelování hemodynamiky mozkových aneuryzmat a možný přínos v klinické praxi z pohledu neurochirurga
- Přehled onemocnění s obrazem restrikce difuze na magnetické rezonanci mozku
- Nové poznatky v diagnostice a léčbě amyotrofické laterální sklerózy
- Léčba recidivy či rezidua multiformního glioblastomu pomocí stereotaktické radiochirurgie gama nožem – společně hodnocený soubor dvou neurochirurgických pracovišť
- Tichý akútny a subakútny mozgový infarkt u pacientov pred koronárnou intervenciou
- Vztah mezi epidemiologií a subjektivním vnímáním bolesti u pacientů se syndromem karpálního tunelu
- Umístění bifurkace bazilární tepny ve vztahu k dorsu sellae
- Validace dotazníku pro pacienty s myotonií – česká verze Myotonia Behaviour Scale
- Zrozumiteľnosť reči a klinické parametre u pacientov s Parkinsonovou chorobou
- První dokumentovaný případ japonské encefalitidy importované do České republiky
- Spinální schwannom v oblasti hrudní páteře s masivním intratumorálním krvácením
- Časná komplikace ošetření disekujícího intrakraniálního aneuryzmatu ve vertebrobazilárním povodí flow-diverterem
- Svalová dystopie ve Fallopiově kanálu
- Harvey Cushing jako kandidát Nobelovy ceny
- Stanovisko Výboru Cerebrovaskulární sekce České neurologické společnosti ČLS JEP k dlouhodobému holterovskému EKG monitoringu u pacientů s ischemickou cévní mozkovou příhodou
- Analýza dat v neurologii LXXI.<br>Pearsonův korelační koeficient
- Recenze knih
- Česká a slovenská neurologie a neurochirurgie
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Nové poznatky v diagnostice a léčbě amyotrofické laterální sklerózy
- Přehled onemocnění s obrazem restrikce difuze na magnetické rezonanci mozku
- Cervikální vertigo – fikce či realita?
- Anestezie a nervosvalová onemocnění
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání








