Analýza dat v neurologii
XXIV. Vybrané příklady hodnocení kategoriálních dat

V tomto díle seriálu pokračujeme ve výkladu hodnocení kategoriálních dat a v sérii příkladů navážeme na předchozí části. Příklady nejsou jen opakováním již vysvětlených témat, ale ukazují i nové přístupy k analýze kontingenčních tabulek (díl XXI). Tyto podněty dodali sami čtenáři našeho seriálu, a tudíž jednotlivá témata probereme systémem otázek a odpovědí. Příklady přibližují analýzy, které většinou nejsou běžně dostupné v nabídce statistických software anebo jejich aplikace vyžaduje určitou znalost a invenci na straně uživatele. Proto jsme výpočty v příkladech doplnili i o matematické vztahy, jež umožní vyzkoušet si výpočet v nějakém dostupném nástroji. Na své si ale, doufejme, přijdou i čtenáři, kteří nemají ambici dané problémy sami hodnotit. Každý příklad je doplněn zadáním problému, zdůvodněním výpočtu a interpretací výsledku.

Otázka 1. Běžné tabulky četností v podstatě dávají do kontrastu výskyt dvou znaků a sledují, zda je mezi kategoriemi určitý vztah, nebo ne. Můžeme ale nějak kvantifikovat odhad četnosti kategorií a rozdílů mezi nimi?

Odpověď je jednoznačně ano. Nezapomeňme, že tabulku četností (např. o velikosti 2 × 2) získáváme výběrem N jedinců, u kterých sledujeme výskyt dvou znaků. Jde tedy o „klasický“ náhodný výběr z cílové populace, a cokoli z tabulky spočítáme, je statistický odhad skutečnosti v oné cílové populaci. I zde platí, že čím máme větší velikost vzorku (N), tím je náš odhad přesnější, a tedy s větší pravděpodobností vystihuje realitu. V tab. 1 to dokumentujeme na příkladu sledování výskytu dýchacích problémů u kuřáků a nekuřáků. Při samotném výběru N jedinců ovšem nesmíme předjímat žádný vztah obou proměnných a výběr musí být zcela náhodný; obě proměnné jsou si rovnocenné.

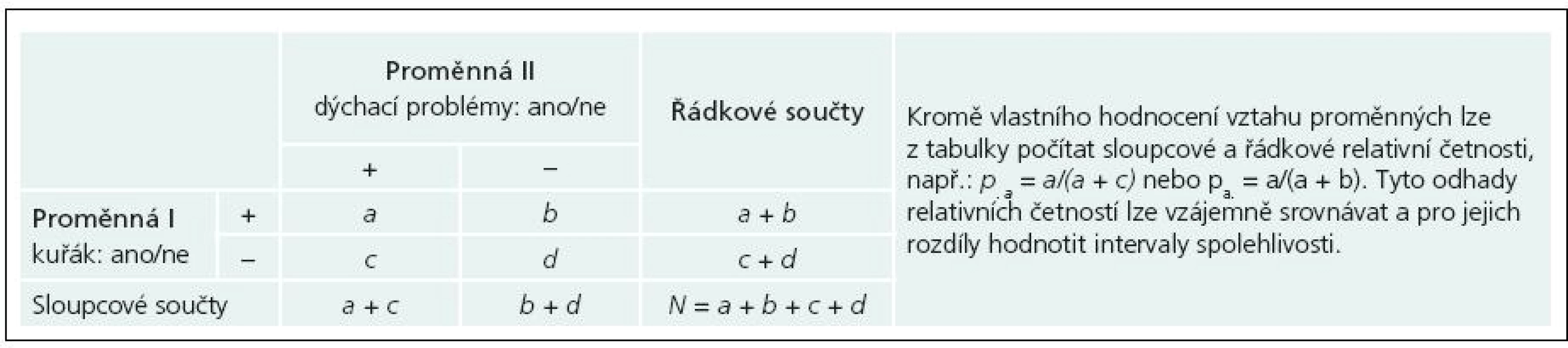
Kromě obecného hodnocení tabulky pomocí χ² testu má samozřejmě význam i parciální analýza výskytu dýchacích problémů mezi kuřáky a nekuřáky. Anebo naopak, srovnání relativního zastoupení kuřáků mezi osobami zdravými a osobami s problémy. Tabulka poskytuje číselné odhady těchto relativních četností. Odborně hovoříme o bodových odhadech. Pro jejich rozdíl je pak možné získat interval spolehlivosti, který má vysokou interpretační hodnotu. Šířka intervalu indikuje spolehlivost provedených odhadů a umožňuje i srozumitelnou prezentaci zjištěných rozdílů. Výpočet takových intervalů přibližuje příklad 1a, b.

Otázka 2. V klinické praxi jsou často mezi sebou srovnávány nežádoucí účinky léčebných metod. Ty mohou být sice hodnoceny jako binární proměnné (ano/ne, prezence/absence), ale častější je jejich hodnocení na určité škále (grade). Existují pro tento problém statistické testy?

Předpokládejme, že se jedná o srovnání v tzv. párovém uspořádání experimentu. Pacientovi je podáván lék 1 a jsou sledovány nežádoucí účinky, poté je lék vysazen a stejné sledování následuje u léku 2. Jde o běžný model uplatňovaný v klinických studiích, např. fáze I nebo II. Příkladem může být sledování ospalosti nebo únavy u léků na sezónní alergii. Pokud u nežádoucích účinků sledujeme prostý výskyt (ano/ne), pak lze pro srovnání léků doporučit tzv. Q-test podle Cochrana, jehož výhodou je, že výpočet přijme i více než dva srovnávané léky. Cochranův test jsme již představili v předchozím díle seriálu jako rozšíření McNemarova testu. Zde uvádíme další, více klinickou aplikaci výpočtu (příklad 2).

Avšak v případě, že jsou nežádoucí účinky zaznamenávány jako stupnice více hodnot odrážející obtížnost problémů (grade), již nevystačíme s McNemarovým ani s Cochranovým testem. Oba testy vyžadují na vstupu binární neboli dichotomickou proměnnou. Naproti tomu škála vyjadřující stupňovitě míru potíží vytváří ordinální proměnnou. Pro párové srovnání založené na ordinální proměnné byl navržen tzv. Bowkerův test. Jeho postup zpracovává K × K tabulku četností, kde jsou obě proměnné vzájemně závislé a jsou zaznamenávány více než dvěma kategoriemi. Označením K × K zdůrazňujeme, že musí jít o tabulku „čtvercovou“, tedy se stejným počtem řádků a sloupců. Při K = 2 je Bowkerův test redukován na již vysvětlený McNemarův test. Výpočet Bowkerova testu přibližujeme v příkladu 3.

Všechny výše zmíněné testy jsou pro hodnocení klinických dat velmi užitečné. Léčebné postupy jsou často sledovány vzájemně závisle na stejných kohortách pacientů. Hodnocení jejich účinnosti a bezpečnosti je běžně prováděno na nominální nebo ordinální škále, nejrůznější skóre „severity“ existují ve většině klinických disciplin. Přesto tyto testy nejsou běžně dostupné v nabídce řady počítačových programů. Jak ale ukazují příklady 2 a 3, výpočet není složitý a lze jej zvládnout i bez specializovaných softwarových nástrojů. Dobře využitelné kalkulátory obou testů se také dají nalézt na internetu, kde v anglickém jazyce hledáme postupy vyhovující tomuto popisu: „Hypothesis tests evaluating changes in mat­ched paired data with binomial or multinomial responses“. V našem jazyce ještě doplníme, že Cochranův i Bowkerův test jsou tzv. testy symetrie tabulky četností.

O prof. W. G. Cochranovi (1909–1980) jsme se již zmínili v předchozím díle seriálu. Rovněž jsme uvedli, že McNemarův test byl publikován v roce 1947. Bowkerův test, nazvaný po svém autorovi, významném americkém statistikovi A. H. Bowkerovi, následoval bezprostředně poté v roce 1948. I přes své stáří nejsou ale tyto testy uzavřenou kapitolou. V recentní literatuře stále probíhá diskuze nad novými aplikacemi těchto postupů, řeší se jejich uplatnění v klinických studiích s různými vzorkovacími plány a jsou vyvíjeny počítačové simulace umožňující podchytit i vzdálenost mezi body ordinální stupnice v Bowkerově testu. Některé zajímavé odkazy uvádíme níže v přehledu literatury. Mimochodem sám autor testu k tomuto výzkumu dlouhá léta přispíval. Test totiž publikoval jako relativně mladý vědec ve věku 29 let. Prof. Bowker zemřel nedávno, v roce 2008, ve věku 88 let.

Otázka 3. Můžeme z tabulky četností hodnotící výskyt dvou znaků usuzovat na jejich korelaci?

Tomuto problému jsme se krátce věnovali již v díle XXI, nicméně pouze výčtem využitelných metod. Korelace je pojem široký, jehož platnost nelze omezit jen na kategoriální data, týká se zejména dat spojitých. Obecně pokud zkoumáme vztah dvou nominálních znaků (ano/ne), hovoříme spíše o významné závislosti nebo asociaci v jejich výskytu. Pojem korelace značí již kvantitativní vyjádření síly takového vztahu a používá se spíše při hodnocení vztahu dvou ordinálních znaků. K měření síly vztahu dvou ordinálních znaků slouží tzv. pořadové koeficienty korelace, kterým se budeme podrobněji věnovat v připravovaných dílech seriálu. Zde jmenujme pouze Kendallův koeficient tau neboli Kendallův korelační koeficient jako míru často využívanou při analýze kontingenčních tabulek. Ukázku jeho výpočtu přináší příklad 4.

Otázka 4. Existuje vzájemná zastupitelnost testů používaných pro hodnocení kontingenčních tabulek?

Jistá zastupitelnost existuje, vždy ale pouze při řešení stejné „třídy“ problémů. Nelze zaměňovat testy určené pro párově (závisle) sledované proměnné s testy pro zcela nezávislé vzorkování výskytu dvou proměnných. Tedy například Fisherův exaktní test (nezávislé uspořádání) nelze v žádném případě zaměnit za McNemarův test (párové uspořádání). A to i přesto, že jsou často ve statistických počítačových programech nabízeny spolu a lze je spočítat současně na stejných datech. Rovněž nelze zaměňovat testy určené pro binární (binomická) data a pro ordinální stupnice. Pokud tato základní pravidla respektujeme, lze někdy pro ověření stanovené hypotézy zvolit i více testů, které jsou alternativně použitelné na stejných datech. Vždy je však nutné sledovat, jakou hypotézu testy hodnotí, a jaká je tedy jejich faktická interpretace; málokdy jde o skutečnou alternativu testování se stejným významem.

Využijeme tohoto problému k menšímu připomenutí tzv. neparametrických testů pro hodnocení dvou pokusných zásahů (díl XVII seriálu). Tyto metody totiž také umožňují pracovat s tabulkami četností vzešlými z nezávislého (Mannův-Whitneyho U test) nebo z párového (Wilcoxonův test) uspořádání experimentu. Problém ale redukují na srovnání výskytu jedné proměnné o dvou kategoriích, jejichž vliv hodnotíme jako „pokusný zásah“. Příklady 5 a 6 připomínají způsob výpočtu těchto testů.

Otázka 5. Je McNemarův test využitelný pro vzájemné srovnání účinnosti laboratorních metod?

Jednoznačně ano, pokud tuto účinnost testujeme striktně párově (tedy obě metody jsou paralelně testovány na stejné sadě vzorků) a sledovanou proměnnou hodnotíme jako binární kód (pozitivita//negativita výsledku; záchyt 1/0; překročena nějaká patologicky kritická hranice ano/ne; apod.). McNemarův test je především test symetrie tabulky četností a sleduje tedy, zda se metody vzájemně liší v četnosti výsledků, kde se neshodují. V příkladu 7 uvádíme ještě alternativní výpočet pomocí znaménkového testu a modelu binomického rozdělení, které doplňují pravděpodobnost, s níž bychom daný výsledek pozorovali zcela náhodně. Můžeme tak přímo posoudit, zda je neshoda obou metod pravděpodobnostně výjimečná, nebo ne.

doc. RNDr. Ladislav Dušek, Dr.

Institut biostatistiky a analýz
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz