DEVELOPMENT PREDICTION OF SAGITTAL ITERMAXILLARY RELATIONS IN PATIENTS WITH COMPLETE UNILATERAL CLEFT LIP AND PALATE DURING PUBERTY

INTRODUCTION

The objective of this study is to find a predictive model for jaw development in patients with complete unilateral cleft lip and palate in the period of pubertal growth spurt. Puberty is crucial for jaw growth and development in facial clefts, and also for orthodontic treatment. Anterior upper jaw growth deficiency may enhance the disproportion in the anteroposterior position of both jaws within a very short time period. This actually leads very often to impaired sagittal intermaxillary relations as well as profile configuration and occlusion of incisors. It may be supposed that as a result of the use of a predicting model in clinical practice, attention would be drawn in time to patients needing intensive orthodontic care. A reduction in the rate of most serious patients requiring maxillofacial surgery should result as well.

LITERARY REVIEW

Many models predicting face growth and development in the healthy population or in patients with less serious growth disorders can be found in the literature (e.g. 2, 3, 7, 11, 17). Prediction of the direction and extension of mandibular growth rotation based on morphological features has been often studied (1, 9, 10, 14). However, the possibilities of predicting facial growth in patients with clefts are very limited, and prediction models are rare so far. A simple system for the prediction of both jaws development was established (4). This method uses individual cephalometric assessment based on specific morphological and morphogenetic face patterns. The procedure consists of two main parts: shape analysis using face growth patterns and sizes of craniofacial structures. This method was applied to clefts by Gnoinska (5) and was conceived as a study of anterior jaw growth as well as the possibility of detection of the first signs of adverse development. The sooner these signs occur, the more disadvantageous is their development. The morphology of the facial skeleton in patients with clefts depended mainly on the following factors: the baseline condition, the surgical intervention and its timing. We consider the poor reliability regarding the location of certain applied points as a disadvantage of this method. Also, the inclination of occlusion plane, representing a substantial part of the system, may undergo quick and significant change as a result of treatment during the mixed dentition period. Schwarz et al. (13) studied options for the utilization of 11 dental arch dimensions in patients with clefts measured prior to surgery for the prediction of subsequently developed lateral cross bite. None of the dimensions used, taken alone, predicted the future development of this pathological deviation. The data were used to calculate multiple predictive equations to accurately forecast cross bite presence or absence in 88% of cases with deciduous, and in 91% of subjects with mixed dentition. Kramer et al. (8) developed a model predicting palatal width and depth in patients with clefts at 4 years of age. The relation between these parameters at 4 years of age and the early growth rate and palate development in the period from birth until 1.5 years of age was submitted to analysis using multi-levelled modelling of longitudinal data. Patients were divided into three groups according to their surgical therapy (without palatal surgery, with repair of the soft palate only, and with surgery of both the soft and the hard palate). Individual predictions were tested and appeared to be possible and purposeful.

A nomogram for the estimation of the failure risk regarding attempts to restore a positive overjet in patients with clefts based on roentgencephalometric assessment of one parameter (interalveolar relations) was developed (15). The system defines critical limits not to be exceeded if the requirements for therapeutic success are to be complied with. However, this system does not involve the development of the jaws and is also unable to predict this development.

In order to establish facial growth prognosis in patients with clefts, Sheuer et al. (12) applied the method of multi-dimensional regression analysis. Equations with correlation coefficients exceeding 0.92 were evolved separately for the estimation of development of the upper and lower jaw protrusion/retrusion (SNA and SNB angles); however, the sagittal intermaxillary relations were not predicted, and prediction was not tested on another patient group.

MATERIAL AND METHOD

The investigation involved 73 boys with complete unilateralcleft lip and palate without other associated malformations,treated at the Clinic of Plastic Surgery inPrague. The patients were monitored during puberty andassessed at the onset and end of this period, i.e. at theages of 10 and 15. The mean age was 10 years and2 months and 15 years and 1 month. 48 patients wereborn between 1972 and 1978, and 25 boys were bornbetween 1985 and 1988.

Primary cheiloplasty performed according to Tennison’s method at an average age of 9 months was associated with periosteoplasty using a 5–7 mm wide and 15–20 mm long periostal flap obtained from the lateral maxillary segment. All patients underwent palatoplasty at a mean age of 5 years, always by the method of pushback with pharyngeal flap surgery. In addition, 25 patients born during the 1980s had primary repositioning of the nasal septum. In about one-third of the patients a tonsillectomy was performed or, in exceptional cases, adenotomy.

Secondary corrective procedures were implemented in patients with persisting soft tissue deformities (64.6%). Corrections of the lip and nose were made in 33.3% of the subjects, correction of the lip in 23% and correction of the nose alone in 8.3%. Fifty patients of the group were treated using fixed appliances, while twenty-three were treated with removable appliances only in order to align the teeth properly in the dental arch and to achieve proclination of the upper incisors and maxillary overjet. The study was based on a craniometric analysis of X-ray films of the patients’ heads made under standard conditions (focus-object distance = 370 cm, object-film = 30 cm, enlargement 8.1%). Cephalometric points and reference lines mentioned in the study are indicated in Fig. 1. In the case of double contours the centre between the right and left side has been marked.

Seventy-one variables were assessed by means of a digitizer: 22 linear, 40 characteristics of position and shape, and 9 dental or special parameters. Measurement of characteristics N-Ss-Pg, Ss-N-Sm and Pr-N-Id is illustrated in Fig. 2, variables Pr+Id and +1/-1 are explained in Fig. 3. Pr+Id is the distance between points Pr and Id after their perpendicular projection to the occlusion plane passing through the midpoint between the cusps of the upper and lower central incisors and molare point (if Pr is posterior in relation to Id, the value is negative). Interincisal angle +1/–1 is the angle between the axis of the upper and lower first incisors.

For statistical processing of the assembled data, the statistical system S-plus 6.2 was used.

The prediction was made on the base of multiple linear regression models and regression partitioning trees (18). Tree-based models provide an alternative to linear and additive models for regression problems, and to linear and additive logistic models for classification problems. Compared to linear and additive models, tree-based models have the following advantages in relation to the analysed data: they allow more general (that is, other than of a particular multiplicative form) interactions between predictor variables, and they also search for deeper relationships between variables based on the tree branches. Prediction was compared with real measurements using paired Wilcoxon rank-sum test and paired t-test at significance level α = 0.05.

RESULTS

The group of 73 long-term follow-up patients made itpossible to propose 2 types of predictive models regardingjaw development in patients with clefts. On the basisof 6 variables at 10 years of age, an equation (Table 1)was created to predict the sagittal intermaxillary relationsat 15 years of age with high reliability (determinationcoefficient R2 = 0.822). In order to test the model itwas calculated 73 times, each time excluding one differentpatient. The parameters of this patient were insertedinto the equation, and in this way we successively establisheda set of 73 predicted values of sagittal intermaxillaryrelations, one for each patient. The real and predictedvalues for each patient were compared with the pairedt-test (t = –0.578, p-value = 0.565) and the Wilcoxon test(z = –0.561, p-value = 0.575), and no difference wasshown using either method (Table 2).

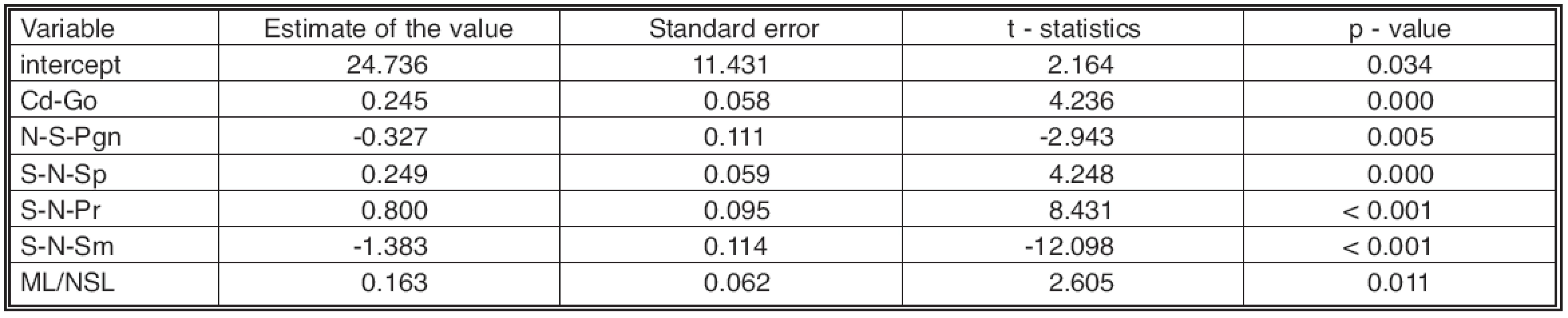
Even though the results obtained indicate the extreme reliability of the model, there is high interindividual variability among the tested patients. The results of our former study (20) proved that groups of similarly developing patients exist, endowed with a similar compensatory adaptation mechanism. Therefore we chose another method, regression partitioning trees. On the basis of a least-square (LS) algorithm, similarly developing patients were grouped into the same clusters with the same predicted values, in our case the ANB angle at 15 years of age. The trees consist of branches defined by intervals of regressor values, which are most connected with the predicted variable. The final model splits our set of 73 patients into six groups that correspond to a certain value of the predicted variable (i.e. ANB). These groups are characterized by one to four variables at 10 years of age (N-Ss-Pg, Pr+Id, +1/–1 and Pr-N-Id), where the tree branches with regard to their size intervals (see Fig. 2).

Six groups of our patients to which the values of the ANB angle at 15 years of age were attributed are as follows: –6.021 (n = 9), –2.529 (n = 12), –0.978 (n = 11), 0.639 (n = 21), 2.078 (n = 13) and 4.300 (n = 7). The final model is based on 4 variables at 10 years of age. The predicted model depends most heavily on face convexity (N-Ss-Pg). A concave face characterized by an angle N-Ss-Pg ≥180.800 degrees predicts in itself the patients with most affected sagittal intermaxillary relations (values of –6.021 and –2.529 degrees). More precisely, an extreme concave face, with convexity angle above 187.800 degrees at 10 years of age, develops during puberty into the model ANB (Ss-N-Sm) angle value –6.021. The ANB angle value of –2.53 degrees is allocated to the face convexity angle in the interval of 187.8–180.8 degrees.

The remaining patient groups may be analyzed in a similar way. Here, other variables at 10 years of age also play a role, namely the sagittal interalveolar relations Pr+Id and the inter-incisal angle +1/–1. For patients with face convexity below 180.800 degrees the borderline value of interalveolar relations (Pr+Id) of 2.550 mm is crucial. If it is above or at this level, sagittal intermaxillary relations develop successfully (model values 2.078 and 4.300 degrees of ANB).

However, from the point of view of orthodontic practice, it is most difficult to make predictions for the last two groups in whom at the age of 15 the ANB angle assumes model values of about zero. If the interincisal angle +1/–1 is greater or equal to 150.300 degrees at 10 years of age, the sagittal intermaxillary relations develop until negative values are reached (–0.978). If it attains values below 150.300 degrees, the ANB angle at 15 years of age reaches the more favourable predicted value of 0.639 degrees.

As with the former model, we compared the actual (measured) and predicted variables by means of the paired t-test (t = –0.002, p-value = 0.999) and the Wilcoxon test (z = –0.380, p-value = 0.648). Neither of the methods yielded any significant difference between predicted and actual values (see Table 2).

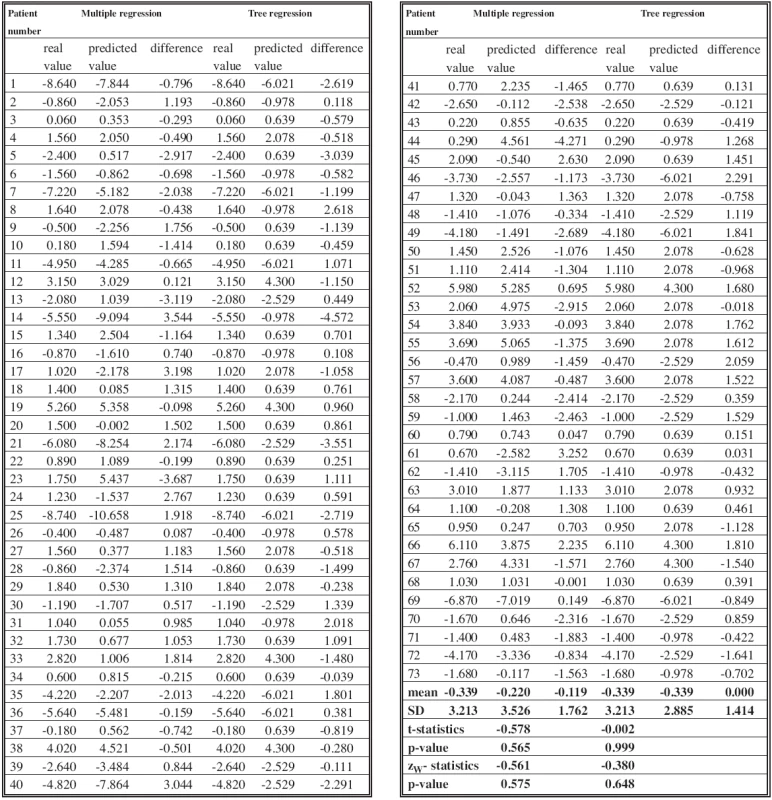
DISCUSSION AND CONCLUSION

Facial clefts produce a high degree of developmental variability of both jaws, making prognosis and therapeutic outlooks very difficult. They represent a specific malformation which is among the most serious skeletal and orthodontic anomalies linked with facial developmental disorders. Therefore predictive systems derived on the basis of findings in subjects free of such malformation cannot be used for patients with clefts. An inherent component in the development of a successful method of prediction is a detailed multivariate analysis of craniometric signs of the patients. We therefore firstmonitored how the single parameters are linked at 10 years of age. The mutual intracranial relations using cluster and factor analysis were investigated (19). Then we concentrated on the longitudinal cephalometric monitoring of facial growth and development between 10 and 15 years of age assessed both according to average statistical characteristics and in individual patients (20). On the basis of these studies a series of trinominal predictive equations was calculated, verified in practice on 12 more patients (21) and published (22).

Models which possess the strongest predictive abilities (R2 of about 0.80) are based on prediction of the ANB angle at 15 years of age. This angle gives good information on therapeutic possibilities and also shows less variability (SD = 1.77) than other characteristics of sagittal jaw relations (Pr-N-Id SD = 1.91, Ss+Sm SD = 2.92, Pr+Id SD = 2.77) (18, 19). The borderline value of the determination coefficient, which is useful for prediction, as verified in orthodontic practice, amounts to about 0.64 (6). Paradoxically, and as confirmed by our present conclusions, the angle ANB at 10 years of age itself is not the strongest regressor in trinomial equations that we proposed. Linear facial dimensions, or more precisely the maxillary height dimensions prior to the pubertal growth spurt, have proved to be among the other important predictive variables (22).

However, the use of the calculated regression tree appears to be a much better and simplex option for practical purposes than trinomial equations. The measurements of only 1 to 4 parameters in a patient at 10 years of age are sufficient for estimation of the ANB angle at 15 years. From the diagram (see Fig. 2) the following conclusions explicitly result:

1. In patients exhibiting facial convexity angle above 180.80 degrees at 10 years of age, the ANB angle below –2.529 degrees at 15 years of age was predicted.

2. In patients with facial convexity angle below 180.80 degrees at 10 years of age and sagittal interalveolar relations (Pr+Id) above 2.55 mm, an ANB angle of at least 2.078 degrees was predicted.

3. In the remaining patients with facial convexity angle below 180.80 degrees and a Pr+Id distance below 2.55 mm, the following predictions may be made using the interincisal angle (+1/–1):

• 3a. An angle below 150.30 degrees predicts an ANB angle of –0.978 degrees.
• 3b. An angle above 150.30 degrees predicts an ANB angle of 0.639 degrees.

These predictive values present sufficient base information on jaw interrelations at 15 years of age and make prediction simpler from the practical point of view.

The series of patients was homogeneous (complete UCLP) and treated with the same primary operations. Some inevitable variations in later treatment, such as in the use of secondary soft tissue procedures or tonsilectomy, do not influence the ANB angle used for prediction, and the same applies to primary repositioning of the nasal septum (16). The impact of the use of fixed appliances on prediction of the ANB angle was also followed up, and no substantial differences as compared to patients with the use of removable appliances alone were found (20).

Our study shows some possible approaches to the still unsolved problem and may contribute to the achievement of better therapeutic results in patients with facial clefts. However, it is necessary to verify the results on patients treated with different procedures and under different conditions.

Acknowledgement: This study was supported by Grant Agency of Charles University 270/2004/B-BIO/PrF and Research plan MSM 0021620843.

Address for correspondence:

Jana Velemínská

Department of Anthropology and Human Genetics

Faculty of Science, Charles University

128 44 Viničná 7, Prague 2

Czech Republic

E-mail: velemins@natur.cuni.cz