-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaŠtúdium lokálnych anestetíkČasť 183: Micelizácia a termodynamické parametre heptakaíniumchloridu v prostredí roztoku KBr
Studies on local anesthetics Part 183: Micellization and thermodynamic parameters of heptacainium chloride in the solution of potassium bromide
The critical micellar concentration (CMC) of the local anaesthetic agent heptacainium chloride in the solution of KBr was determined by the spectrophotometric method in the UV region of the spectrum at the temperature range of t = 20–40 °C and pH ≈ 4.5–5.0. The dependence of CMC on the temperature T turned out forming the U-shape with the minimum at the temperature of t = 25 °C. The parabolic dependence of CMC on the temperature T was drawn by the fitting of the values using the polynomial function and the so-called power law equation. The CMC dependence on the temperature T was fitted by the second degree polynomial function. The obtained parabolic equations were applied to the “phase separation model”, so the following thermodynamic parameters could be calculated: standard Gibbs free energy (∆G°), enthalpy (∆H°), and entropy (∆S°). The thermodynamic parameters were further used to determine the so-called entropy-enthalpy compensation of the systems under study. The compensation temperature was in the following range: (30 ± 1–303 ± 3)K. Then the temperature dependence of the enthalpy (∆H°) and entropy (–T∆S°) contributions to the standard Gibbs free energy (∆G°) for all prepared concentrations of the compound were calculated.
Key words:
heptacainium chloride – critical micellar concentration (CMC) – thermodynamics – standard Gibbs free energy – enthalpy – entropy.
Autoři: F. Andriamainty; J. Čižmárik; I. Malík; S. Horvat
Působiště autorů: Univerzita Komenského Bratislava, Farmaceutická fakulta, Katedra farmaceutickej chémie
Vyšlo v časopise: Čes. slov. Farm., 2008; 57, 119-125
Kategorie: Původní práce
Souhrn
Kritická micelová koncentrácia lokálneho anestetika heptakaíniumchloridu v prostredí KBr (0,1 mol/l a 0,2 mol/l) bola určená spektrofotometricky v UV oblasti spektra v teplotnom intervale t =2 0–40 °C a pri pH ≈ 4,5–5,0. Závislosť CMC od teploty T mala tvar „U“ (U-shaped) s minimom pri teplote t = 25 °C. Parabolická závislosť CMC od teploty T bola fitovaním hodnôt charakterizovaná pomocou tzv. „power-law“ rovnice. Zo závislosti ln (CMC) od T sme fitovaním polynómom druhého stupňa získali parabolické rovnice pre jednotlivé koncentrácie študovanej látky, z ktorých boli pomocou modelu fázovej separácie vypočítané termodynamické parametre, ako sú: štandardná mólová Gibbsova energia (∆G°), entalpia (∆H°) a entropia (∆S°). Z termodynamických parametrov bola ďalej určená tzv. „enthalpy-entropy“ kompenzácia pre študované prostredia. Kompenzačné teploty Tc sa pohybovali v rozmedzí (301 ± 1–303 ± 3) K. Napokon boli určené energetické príspevky entalpie (∆H°) a entropie (–T∆S°) k štandardnej mólovej Gibbsovej energii (∆G°).
Kľúčové slová:
heptakaíniumchlorid – kritická micelová koncentrácia (CMC) – termodynamika – štandardná mólová Gibbsova energia – entropia – entalpiaÚvod
O aktivite derivátov kyseliny fenylkarbámovej ako lokálnych anestetík sa po prvýkrát vo svojej práci zmienil Fromherz 1), ktorý predpokladal, že zavedením karbamátovej NH-COO-skupiny do molekuly lokálnych anestetík sa potlačí jeden z najčastejších nežiaducich účinkov – stimulácia centrálnej nervovej sústavy.
Medzi zlúčeniny s vysokou lokálne anestetickou aktivitou patria bázické estery kyseliny alkoxyfenylkarbámovej. Súvisí to s koreláciou medzi fyzikálno-chemickými parametrami (rozdeľovací koeficient, schopnosť znižovať povrchové napätie) lokálnych anestetík a ich biologickou účinnosťou. Substitúcia aromatického jadra molekuly alkoxysubstituentami, ktoré zvyšujú lipofilitu, je potrebná pre dosiahnutie intenzívneho lokálneanestetického účinku. Avšak vysoká lipofilita a povrchová aktivita naznačuje možnosť ich cytotoxického účinku 2).
Čižmárik et al. v rámci štúdia vplyvu alkoxysubstitúcie na lokálne anestetickú aktivitu bázických esterov kyseliny fenylkarbámovej pripravili homologickú sériu 30 látok, piperidínoetylesterov kyseliny 2-, 3-, 4 - alkoxyfenylkarbámovej 3).
U týchto látok boli uskutočnené farmakologické testy na lokálne anestetický účinok pri povrchovej a infiltračnej anestézii, ako aj testy akútnej toxicity. Všetky syntetizované látky vykazovali výrazne vyšší lokálneanestetický účinok ako ich analogické halogén - alebo alkylderiváty. Najúčinnejšou látkou z uvedenej série alkoxyfenylkarbamátov je heptakaín, chemicky N-[2--(2 heptyloxyfenylkarbamoyloxy)-etyl]piperidínium-chlorid, pracovne označovaný ako látka XIX. Jej farmakologické štúdium ukázalo, že je 100-násobne účinnejšia pri povrchovej anestézii ako štandard kokaín a 171-násobne účinnejšia pri infiltračnej anestézii ako štandard prokaín 3).
Lokálne anestetiká patriace do skupiny bázických esterov substituovaných kyselín alkoxyfenylkarbámových sa vyznačujú povrchovou aktivitou, t.j. schopnosťou znižovať povrchové napätie vody. Majú teda vlastnosti tenzidov. Tieto sú podmienené ich amfifilnou štruktúrou, odrazom ktorej je tiež správanie alkoxyfenylkarbamátov vo vodnom prostredí. Amfifilné látky sa po prekročení kritickej micelovej koncentrácie (CMC) spontánne zhlukujú do väčších agregátov, tzv. miciel. Hodnota kritickej micelovej koncentrácie je ovplyvnená nielen ich chemickou štruktúrou, ale aj faktormi, akými sú teplota, prímesi elektrolytov či alkoholov 4–6).
Vo svojich doterajších prácach sme študovali termodynamické parametre heptakaíniumchloridu s prímesou elektrolytov NaCl a KCl, poprípade s prídavkom metanolu, etanolu a propanolu. Kedže na termodynamické parametre majú značný vplyv aj anióny prímesi elektrolytu, v tejto práci sme zvolili KBr pre väčší rozmer Br- ako má Cl-.
V predkladanej práci sme sa zamerali preto na stanovenie kritickej micelovej koncentrácie (CMC) heptakaíniumchloridu v prostredí roztoku KBr spektroskopickou metódou.
POKUSNÁ ČASŤ
Študované látky a prístroje
Heptakaíniumchlorid bol pripravený na Katedre farmaceutickej chémie FaF UK v Bratislave podľa práce 3).
Prístroje
Spectrofotometer HP 8452 A Diode Array (Hewlett Packard, Nemecko); analytické váhy (WA 33 typ PRL T A 13/1, Techma Robot, Poľsko); pH meter (Portamess 943 pH, Elekronische Messgeräte GmbH Co., Nemecko); Termostat (Veb ML W Prüfgerate-Werk Medingen / Sity /, Nemecko).
Pracovný postup
Pripravili sme zásobné roztoky študovanej látky XIX s koncentráciou c = 10-3 mol/l rozpustením stanoveného množstva látky v 0,1 mol/l a 0,2 mol/l roztokoch bromidu draselného.
Z jednotlivých základných roztokov sme pripravili sériu roztokov s klesajúcou koncentráciou riedením destilovanou vodou. Pri každej koncentrácii sme pri teplotách t = 20oC, 25 oC, 30 oC, 35 oC a 40 oC a pH ≈ 4,5–5,0 zaznamenávali priebeh spektra danej látky proti porovnávaciemu roztoku (príslušný základný roztok KBr) v ultrafialovej oblasti spektra v rozsahu vlnových dĺžok 190–350 nm. Zaznamenali sme hodnoty absorbancie pri vlnovej dĺžke λmax = 234 nm.
Model fázovej separácie (Pseudofázový model)
Pseudofázový model je jednoduchší ako model založený na pôsobení aktívnych hmotností. Jeho jednoduchosť umožňuje využitie pri zmiešaných tenzidoch, čo pri druhom modele nie je možné. Podľa modelu fázovej separácie možno zmenu štandardnej mólovej Gibbsovej energie vypočítať pomocou vzťahu 7):
ΔG° = γRT ln(CMC), [1]
kde γje stupeň viazania protiiónov, R je plynová konštanta a T je absolútna teplota.
Podľa zvoleného modelu γmôže nadobúdať nasledovné hodnoty:
(PS1):γ = 1, keď sú protiióny úplne ionizované.
(PS2):γ = 2, keď sú všetky protiióny viazané do micely.
Štandardnú mólovú entalpiu micelizácie možno určiť aplikáciou Gibbs-Helmholtzovej rovnice zo vzťahu:
Hodnotu entrópie počítame podľa základnej rovnice:
Závislosť ln(CMC) od teploty, t.j. ln(CMC) = f(T), má charakter polynomickej funkcie druhého stupňa, pre ktorú platí nasledovná rovnica:
ln(CMC) = f(T) = A + BT + CT2 [4]
kde A, B, C sú konštanty polynómu a T je absolútna teplota.
Štandardnú mólovú Gibbsovu energiu možno počítať po dosadení rovnice [4] do rovnice [1] podľa vzťahu:
ΔG° = γRT(A + BT + CT2). [5]
Obdobnou úpravou – dosadením rovnice [4] do rovnice [2] – získame vzťah pre výpočet štandardnej mólovej entalpie:
ΔH° = –γRT2(B + 2CT). [6]
Závislosť kritickej micelovej koncentrácie od teploty
Závislosť kritickej micelovej koncentrácie (CMC) od teploty (T) nemá lineárny priebeh, ale vykazuje pri určitej teplote tzv. teplotné minimum CMC. Predpokladá sa, že vplyv teploty na CMC je vyvolaný predovšetkým koncovými časťami molekúl, ktoré spôsobujú hydrofóbne väzby.
Toto teplotné minimum (T*) je ľahko zistiteľné fitovaním závislosti kritickej micelovej koncentrácie (CMC) od teploty (T) polynómom druhého alebo vyššieho stupňa. Stupeň polynomickej funkcie závisí od kvality údajov a od množstva bodov na grafe závislosti kritickej micelovej koncentrácie (CMC) od teploty (T). Teplotnému minimu (T*) zodpovedá minimálna kritická micelová koncentrácia (CMC*).
Závislosť kritickej micelovej koncentrácie od teploty môžeme popísať rovnicou „power law“ 8):
|CMCr – 1| = A.|Tr – 1|n [7]
alebo
kde CMCr je redukovaná kritická micelová koncentrácia, Tr je redukovaná teplota, A je konštanta a n je exponent charakteristický pre daný systém tenzidu.
Dôležitosť tohto vzťahu spočíva v tom, že po získaní hodnôt A a n pre daný systém je možné predpovedať hodnotu kritickej micelovej koncentrácie pri ktorejkoľvek teplote.
Pre CMCr a Tr platí:
Zlogaritmovaním vzťahu [7] dostaneme:
log|CMCr – 1| = log A + nlog|Tr – 1|, [11]
kde log A je konštanta a n je smernica závislosti log|CMCr – 1| od log|Tr – 1|.
Vzájomná kompenzácia medzi entalpiou a entropiou
Rozmanitosť procesov určitej rozpustenej látky vo vodnom roztoku takých, ako je napr. oxidácia-redukcia, hydrolýza atď., ukazuje lineárny vzťah medzi zmenami entropie a entalpie. Tento fenomén je známy ako „enthalpy-entropy“ kompenzácia 9). Proces micelizácie tenzidov prebieha tiež ako kompenzačný fenomén.
Hydrofóbny efekt spôsobený interakciou medzi koncom uhľovodíkového reťazca tenzidu a vodou zohráva dôležitú úlohu vo vytváraní miciel. Lumry a Rajender popísali micelizáciu podľa tohto fenoménu dvomi čiastkovými procesmi 10):
1. „desolvatačná časť“ – dehydratácia uhľovodíkového reťazca molekuly tenzidu.
2. „chemická časť“ – agregácia uhľovodíkového reťazca molekuly tenzidu a vytvorenie miciel.
Vo všeobecnosti možno kompenzačný jav medzi zmenami entalpie a entrópie prebiehajúcou v rozličných procesoch popísať nasledovne:
ΔH°m = ΔH*m + TcΔS°m [12]
kde ΔH°m je zmena štandardnej mólovej entalpie, ΔH*m je konštanta tzv. „intercept“ (úsek), smernica Tc je známa ako kompenzačná teplota a ΔS°m je zmena štandardnej mólovej entrópie.
Kompenzačná teplota (Tc) môže byť interpretovaná ako charakteristika „solute-solute” interakcií alebo „solute-solvent” interakcií, teda je navrhovaná ako miera desolvatačnej časti procesu micelizácie. Úsek ΔH*m charakterizuje interakciu „solute-solute” je považovaný za ukazovateľa chemickej časti procesu micelizácie 11).
VÝSLEDKY A DISKUSIA
Hodnotu CMC sme určili ako priesečník dvoch extrapolovaných kriviek, ktoré interpretovali závislosť absorbancie A ako funkciu koncentrácie c 12). Na extrapoláciu kriviek sme použili komerčný program OriginPro 7.5 (http://www.OriginLab.com).
Hodnoty CMC sa pohybovali v rozmedzí od 4,1215.10-4 mol/l do 4,1741.10-4 mol/l v 0,1 mol/l roztoku KBr, a od 4,4038.10-4 mol/l do 4,4578.10-4 mol/l v 0,2 mol/l roztoku KBr.
Hodnoty CMC, ln(CMC) v závislosti od T (K) sú zaznamenané v tabuľkách 1 a 2. Hodnoty ln(CMC) v závislosti od teploty T sú uvedené na obrázkoch 1 a 2. Závislosť ln(CMC) od teploty mala tvar „U“ („U-shaped“). Hodnoty boli fitované polynómom druhého stupňa. Polynomické rovnice (y = ln(CMC) = A + B.T + C.T2) a korelačné koeficienty (R) látky XIX v 0,1 mol/l, resp. 0,2 mol/l roztokoch KBr boli nasledovné:
Tab. 1. Zistené hodnoty CMC a ln(1/CMC) pri látke XIX v 0,1 mol/l roztoku KBr 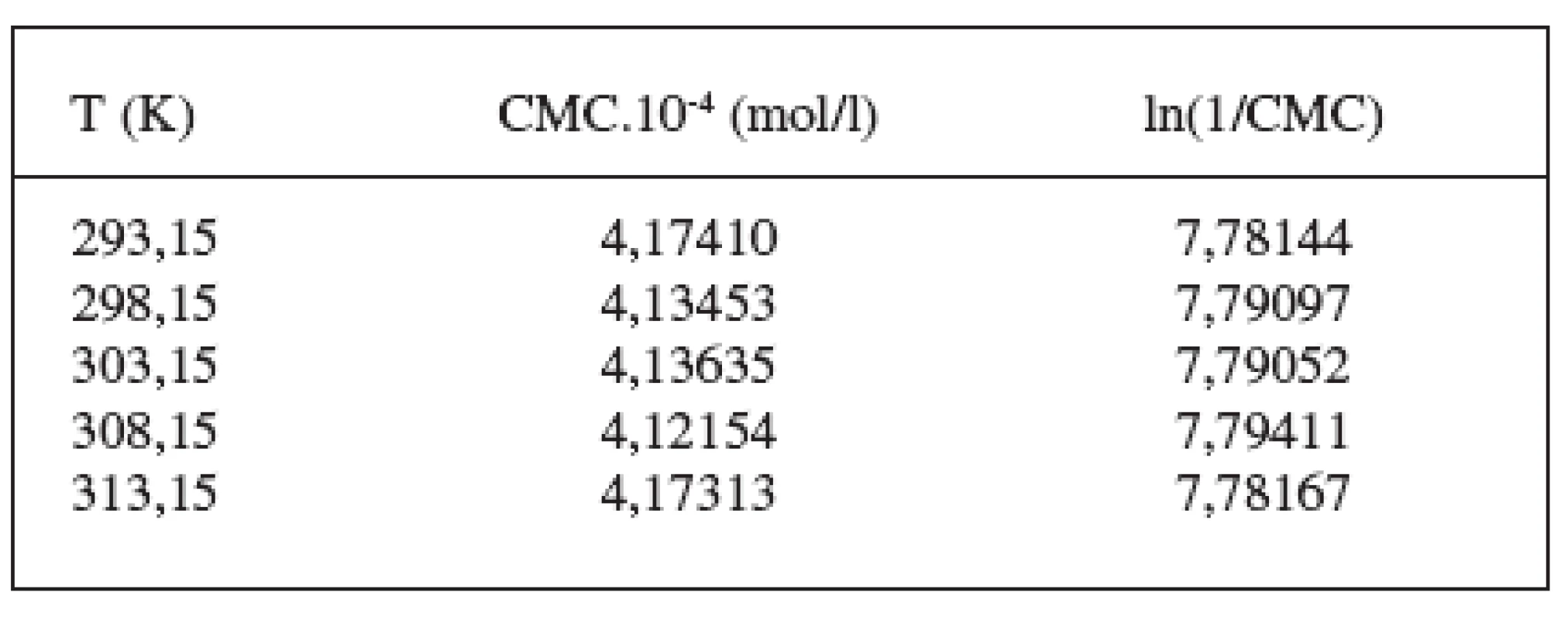
Tab. 2. Zistené hodnoty CMC a ln(1/CMC) pri látke XIX v 0,2 mol/l roztoku KBr 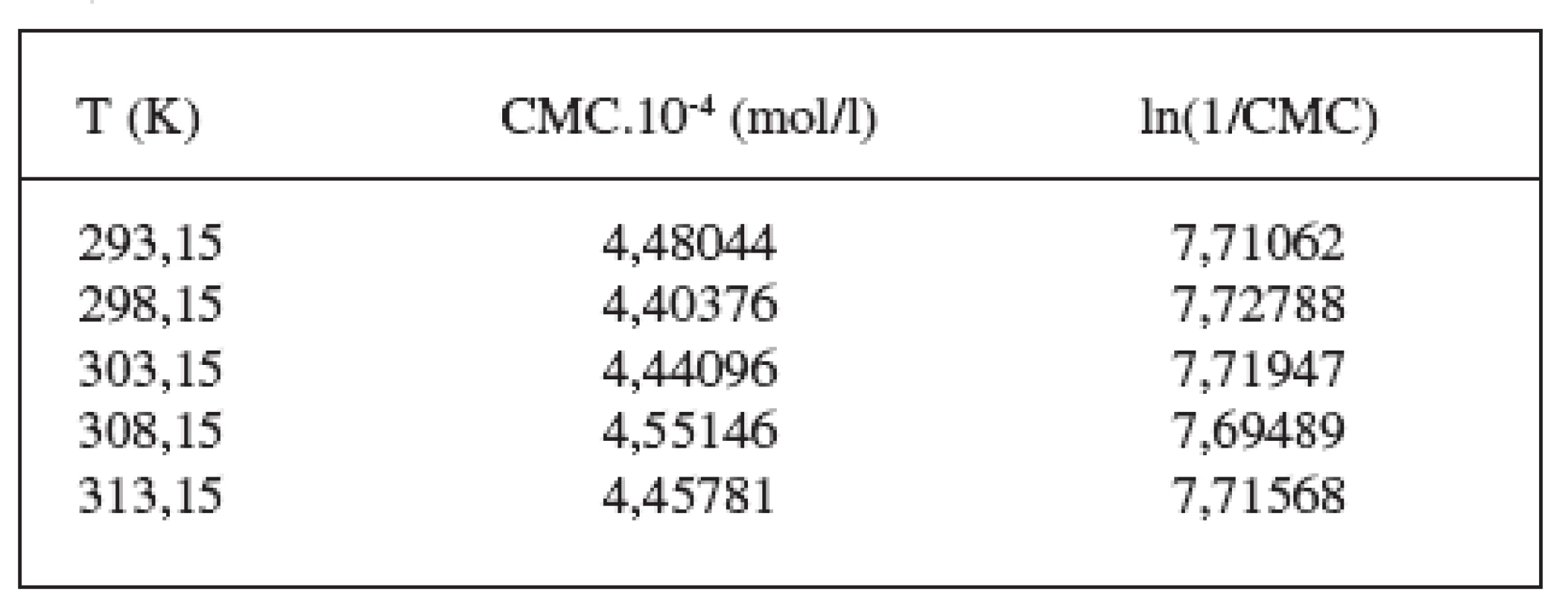
Obr. 1. Závislosť ln(CMC) od T pre látku XIX (0,1mol/l KBr) 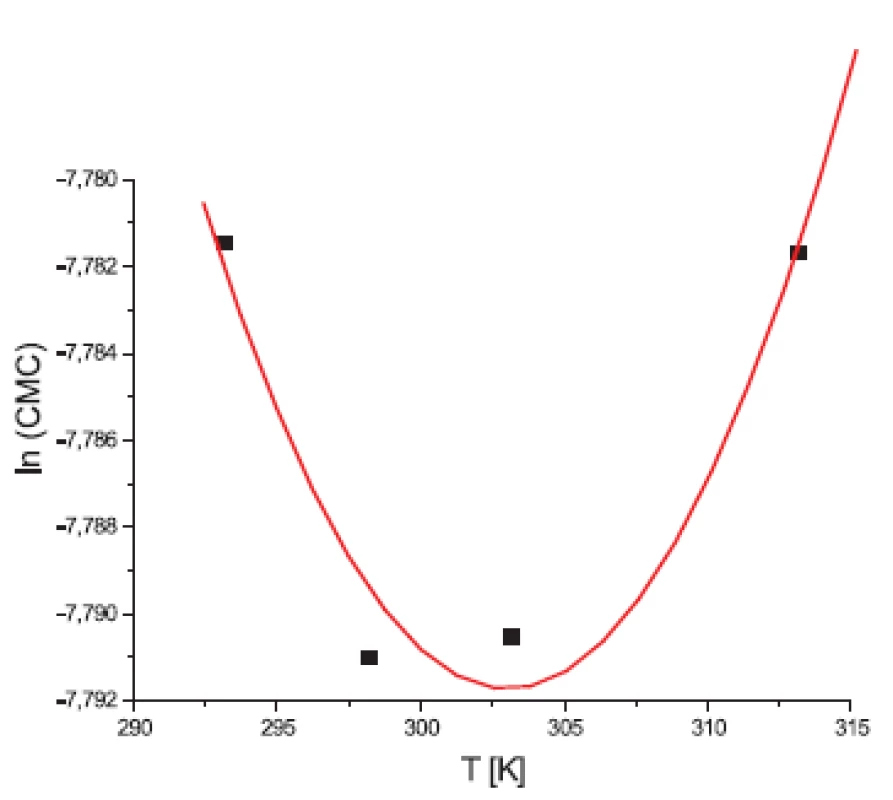
Obr. 2. Závislosť ln(CMC) od T pre látku XIX (0,2 mol/l KBr) (0,2 mol/l KBr) 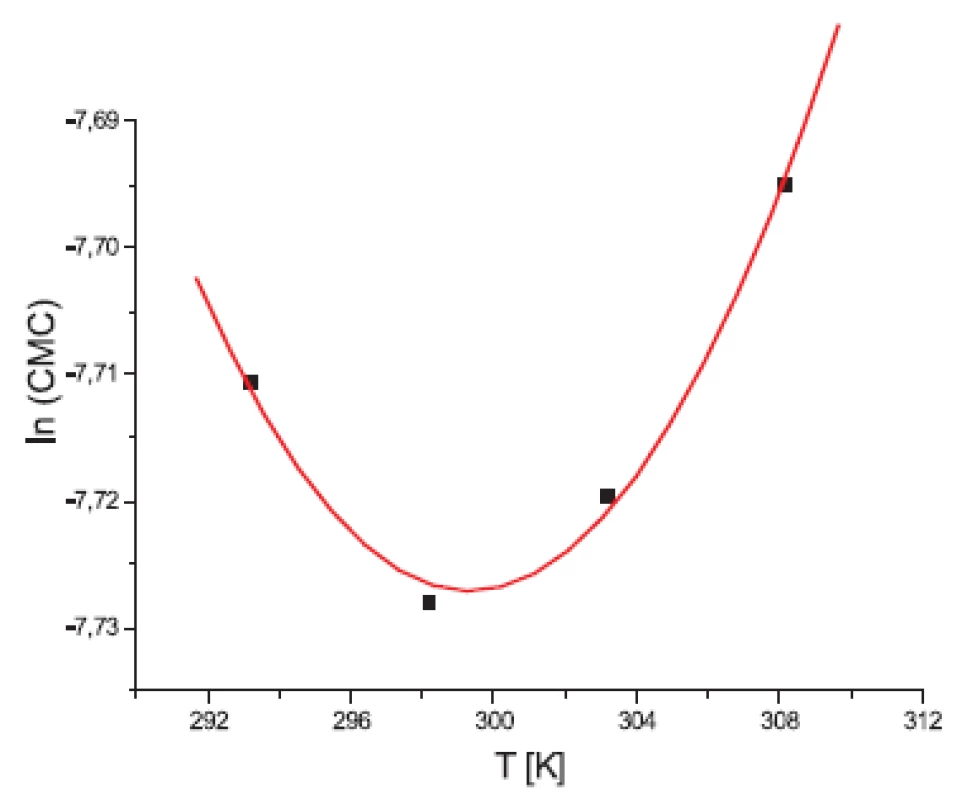
y = ln(CMC) = (1,36 Ī 2,18) + (-0,0604 Ī 0,0144)T + (9,964 Ī 2,365).10-5 T2;
R = 0,974; N = 4 (0,1 mol/l KBr)
a
y = ln(CMC) = (29,76 Ī 3,84) + (-0,2505 Ī 0,0255)T + (41,840 Ī 4,248).10-5 T2;
R = 0,996; N = 4 (0,2 mol/l KBr).
Hodnota ln(CMC) s teplotou klesala až po T = 302,52 K v 0,1 mol/l roztoku KBr a až po T = 299,23 K v 0,2 mol/l roztoku KBr a potom stúpala. Predpokladáme, že tento postupný pokles CMC je zapríčinený desolvatačným procesom prebiehajúcim na koncovej časti postranného reťazca. V minime CMC nastal zlom, po ktorom bol pozorovaný nárast CMC, čo je pravdepodobne spôsobené agregáciou uhľovodíkového reťazca a vytvorením miciel tak, ako je to vysvetlené v práci 11).
Ďalej sme študovali závislosť CMC od T a tzv. „power law“ rovnice. Hodnoty CMC v závislosti od T boli fitované polynómom druhého stupňa. Z grafov sme získali hodnoty C*CMC(najnižšia dosiahnutá koncentrácia) a T* (najnižšia dosiahnutá teplota). Tieto hodnoty sú v tabuľke 3. Ako bolo spomenuté v pokusnej časti, môže byť závislosť CMC od teploty T definovaná tzv. „power law“ rovnicou, ktorú sme získali fitovaním hodnôt redukovanej teploty (Tr) a redukovanej CMC (CMCr). Hodnoty CMC, T, CMCr, Tr resp. log|CMCr – 1|, log(Tr – 1) sú v tabuľkách 4 a 5. Na obrázkoch 3 a 4, z ktorých boli získané hodnoty A (konštanty) a n (exponent) fitovaním hodnôt lineárnou funkciou, je zaznamenaná závislosť log|CMCr – 1| od log(Tr – 1). Hodnoty konštánt A a exponentov n (tab. 6) sú charakteristické pre jednotlivé látky a umožňujú výpočet neznámej CMC.
Tab. 3. Hodnoty CMC* (mol/l) a T* (K) pre látku XIX v 0,1 mol/l a v 0,2 mol/l roztokoch KBr 
Tab. 4. Hodnoty CMC, T, CMCr, Tr resp. log(CMCr – 1), log(Tr – 1) pre látku XIX (0,1mol/l KBr) 
Tab. 5. Hodnoty CMC, T, CMCr, Tr resp. log(CMCr – 1), log(Tr – 1) pre látku XIX (0,2 mol/l KBr) 
Obr. 3. Závislosť log(CMCr – 1) od log(Tr – 1) – látka XIX (0,1 mol/l KBr) 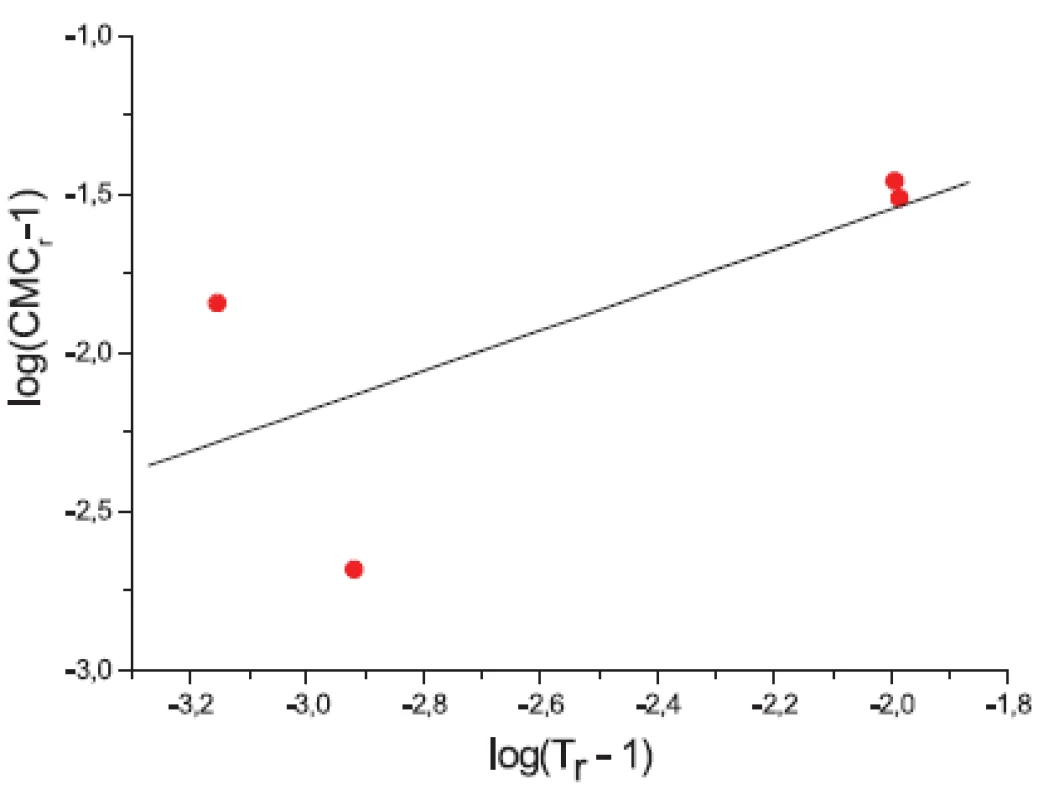
Obr. 4. Závislosť log(CMCr – 1) od log(Tr – 1) – látka XIX (0,2 mol/l KBr) 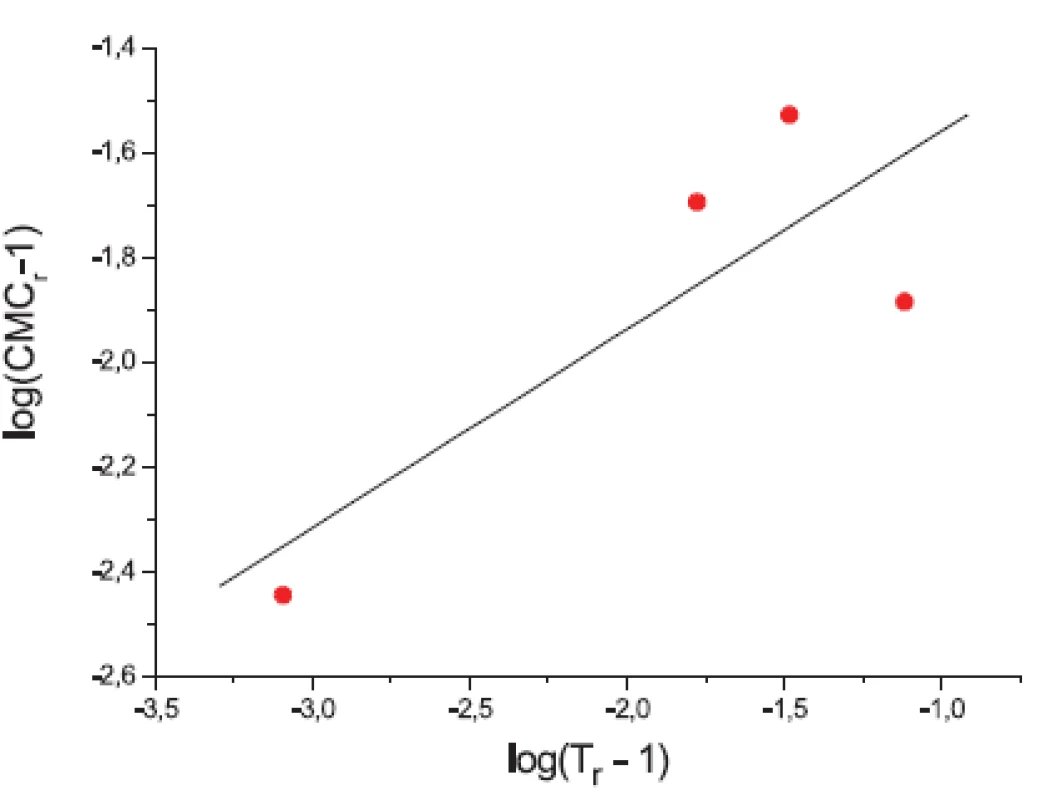
Tab. 6. Hodnoty konštanty A a exponentu n tzv. „power law” rovníc pre jednotlivé koncentrácie (0,1 mol/l a 0,2 mol/l KBr) 
V práci sme sa ďalej zamerali na výpočet termodynamických parametrov micelizácie: štandardnej mólovej Gibbsovej energie ∆G° (kJ.mol-1), entalpie ∆H° (kJ.mol-1) a entropiu ∆S° (kJ.mol-1.K-1). Tieto parametre sme počítali podľa modelu fázovej separácie (PS) komerčným programom Power Basic. Na obrázkoch 5 a 6 sme uvádzali závislosť termodynamických veličín ∆G°, ∆H° a T∆S° od teploty T (K).
Obr. 5. Termodynamické parametre látky XIX v 0,1 mol/l KBr 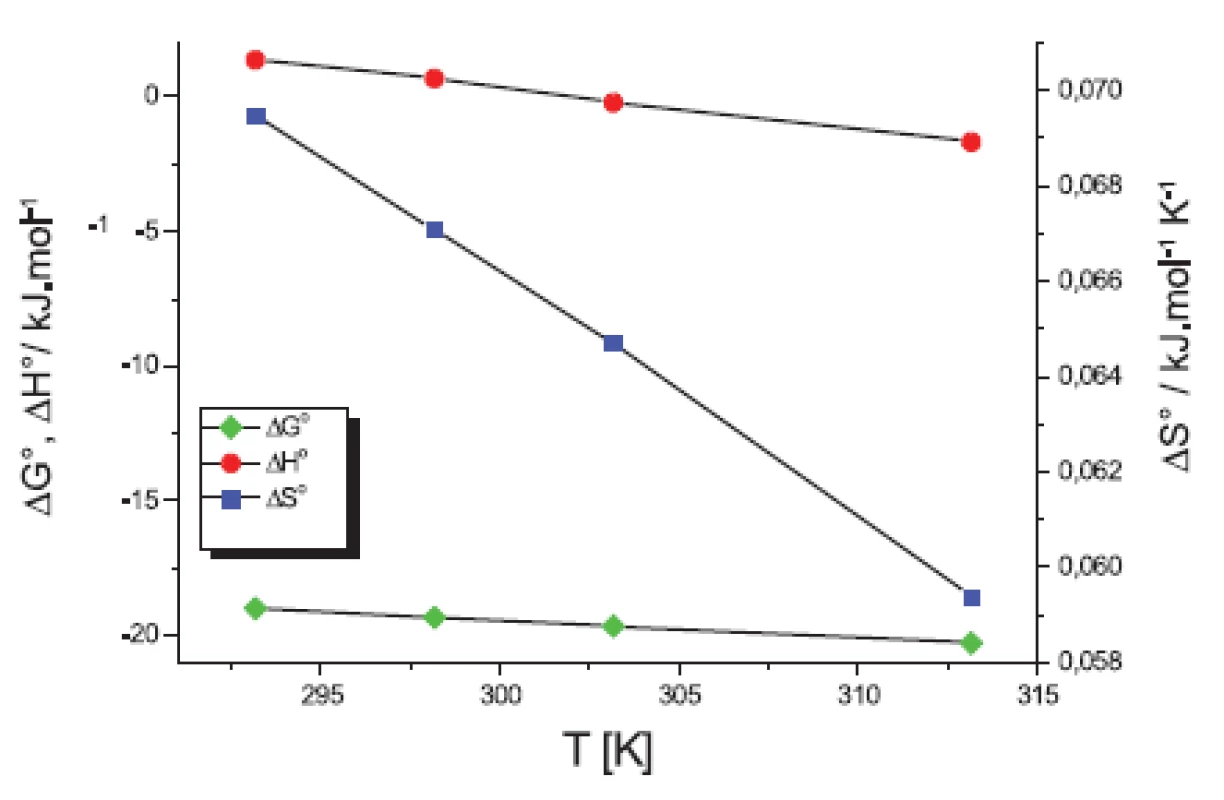
Obr. 6. Termodynamické parametre látky XIX v 0,2 mol/l KBr 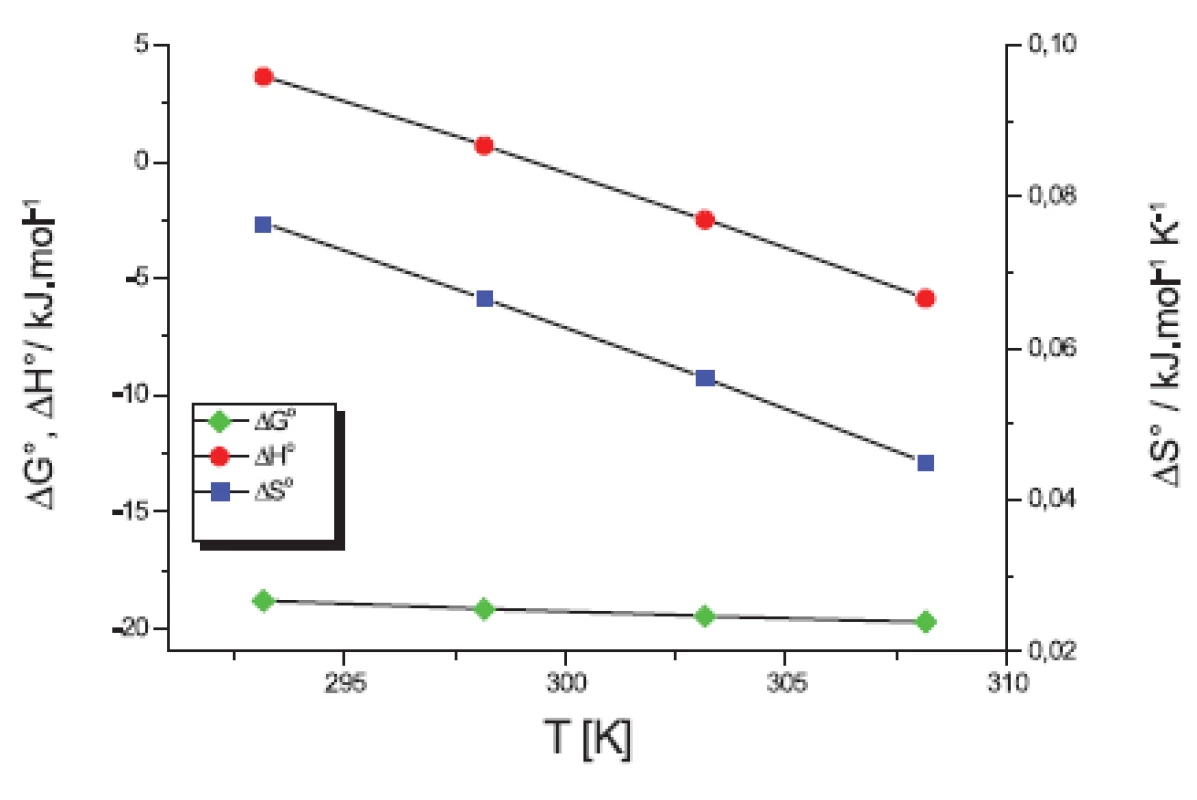
Na obrázkoch 5 a 6 môžeme vidieť, že štandardná mólová Gibbsova energia ∆G° (kJ.mol-1) je záporná a s teplotou sa mení len veľmi málo. Výraznejší je pokles entalpie ∆H° (kJ.mol-1). Z týchto výsledkov vyplýva, že micelizačný proces sa so zvyšujúcou teplotou stáva exotermickejším. K podobným záverom sme dospeli v predchádzajúcich prácach 13, 14). Hodnoty entropie ∆S° (kJ.mol-1.K-1) sú kladné a klesajú so stúpajúcou teplotou.
Hodnota štandardnej mólovej Gibbsovej energie ∆G° je tvorená príspevkami entalpie ∆H° a entropie -T∆S°. Jednotlivé príspevky sú zaznamenané na obrázkoch 7 a 8. Fitovaním hodnôt pomocou polynómu prvého stupňa sme získali lineárne rovnice. Na týchto grafoch vidíme, že k prieniku by došlo až pri vyšších teplotách. Teploty, pri ktorých boli príspevky rovnaké, sú zaznamenané v tabuľke 7.
Obr. 7. Príspevky entalpie (ΔH°) a entropie (-TΔS°) k štandardnej mólovej Gibbsovej energii (ΔG°) látky XIX (0,1 mol/l KBr) 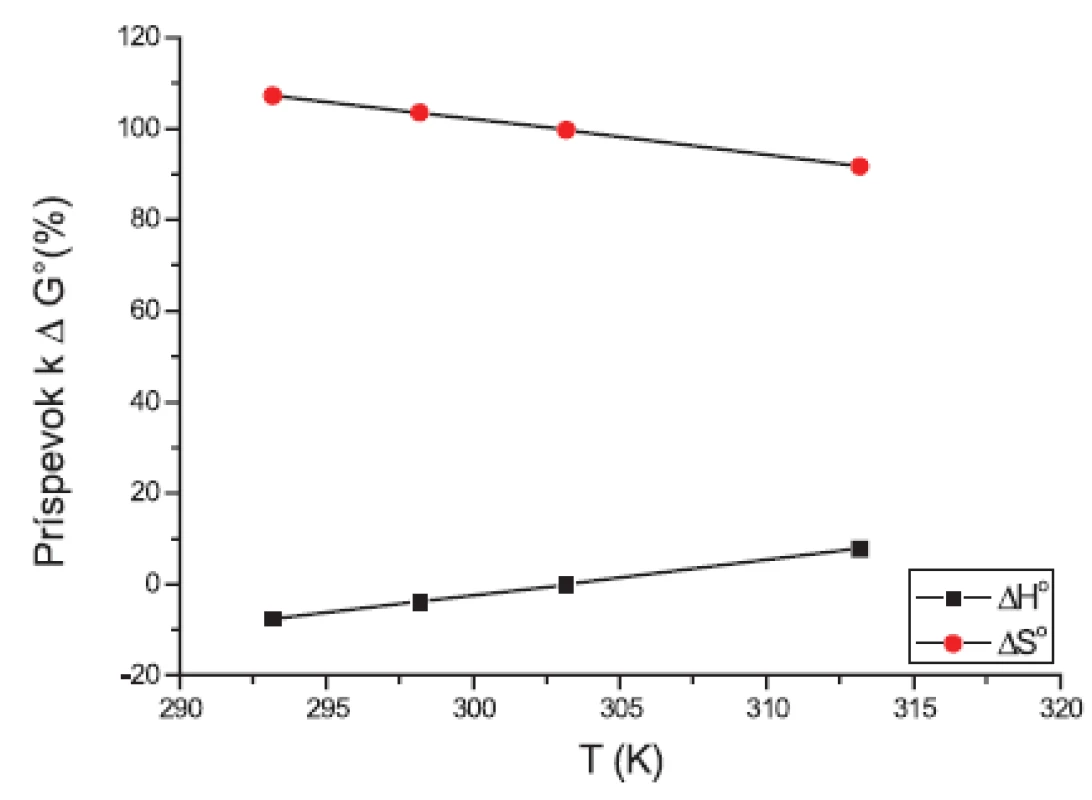
Obr. 8. Príspevky entalpie (ΔH°) a entropie (-TΔS°) k štandardnej mólovej Gibbsovej energii (ΔG°) látky XIX (0,2 mol/l KBr) 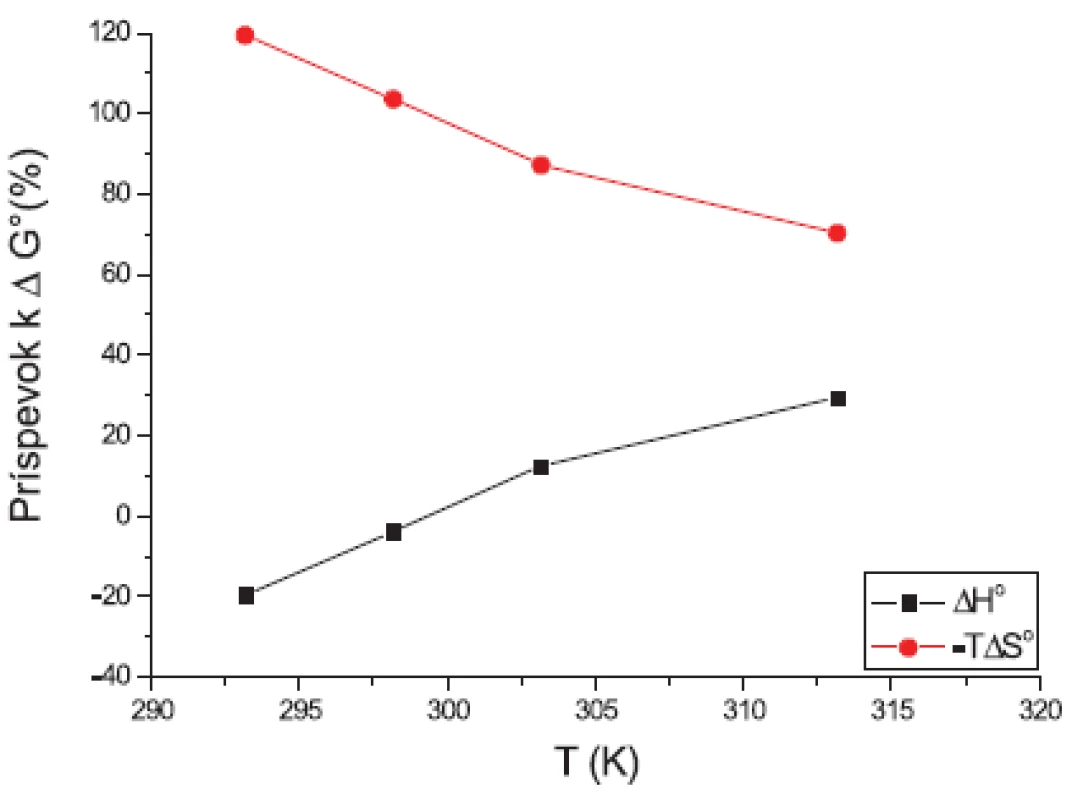
Tab. 7. Teploty, pri ktorých boli príspevky entalpie (ΔH°) a entropie (-TΔS°) k štandardnej mólovej Gibbsovej energii (ΔG°) zhodné 
Závislosť medzi entropiou (ΔS°) a entalpiou (ΔH°) látky XIX v 0,1 mol/l, resp. 0,2 mol/l roztokoch KBr je zaznamenaná na obrázkoch 9 a 10. Pozorovaný lineárny priebeh spôsobujú rozličné chemické procesy. Tento fenomén je známy ako „enthalpy-entropy” kompenzácia. Výsledné rovnice a korelačné koeficienty (R) sú:
Obr. 9. Závislosť ΔH° od ΔS° pre látku XIX (0,1 mol/l KBr) 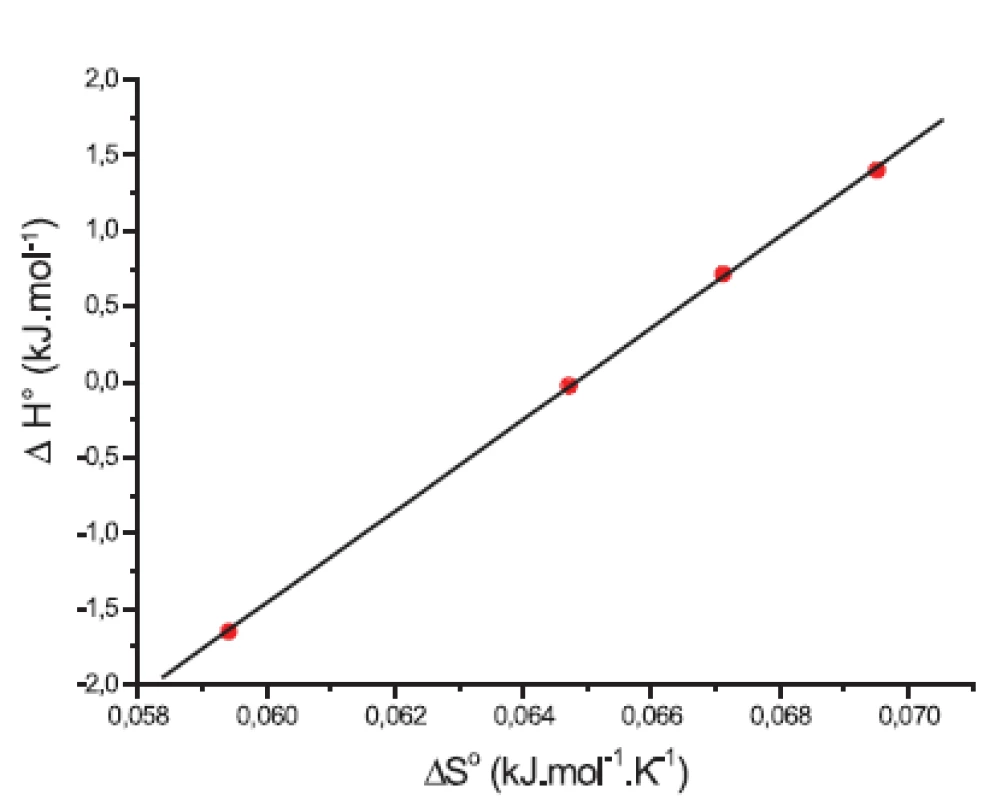
Obr. 10. Závislosť ΔH° od ΔS° pre látku XIX (0,2 mol/l KBr) 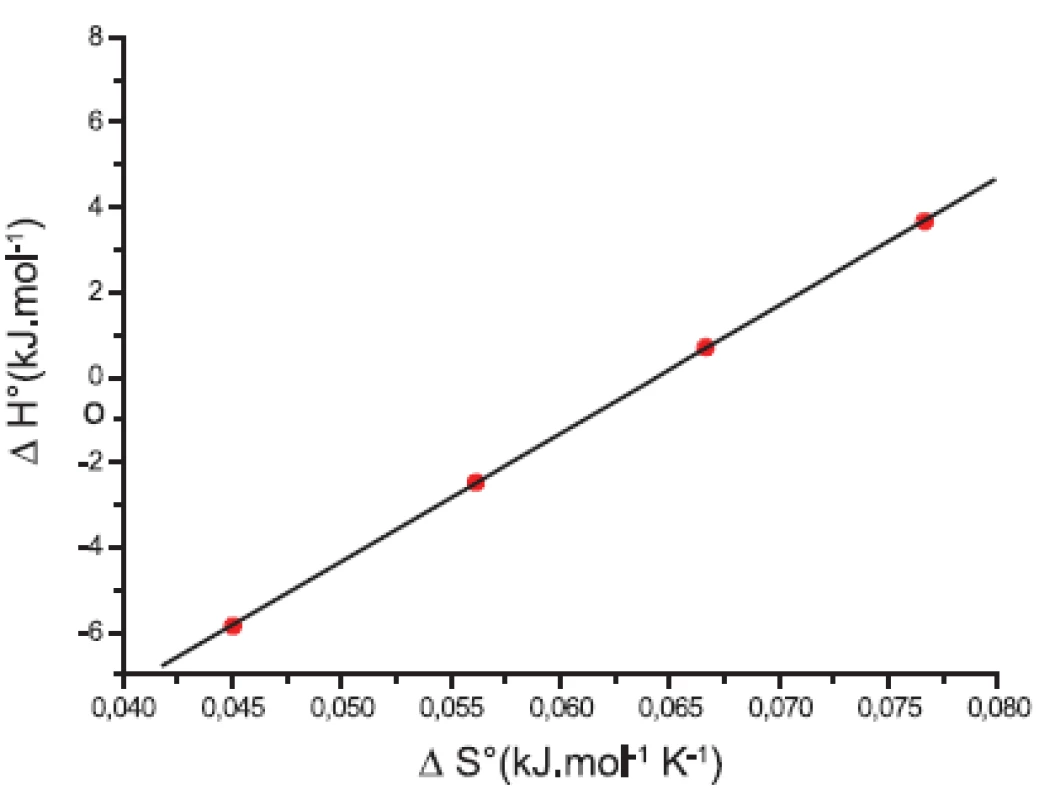
y = (-19,63 Ī 0,19) + (303,02 Ī 2,94) x;
R = 0,999; N = 4 (0,1 mol/l KBr)
a
y = (-19,37 Ī 0,08) + (301,31 Ī 1,33) x;
R = 0,999; N = 4 (0,2 mol/l KBr).
Z rovníc sme určili tzv. kompenzačné teploty (smernice závislosti), ktoré sú zaznamenané v tabuľke 8. Kompenzačné teploty Tc (K) boli (303 Ī 3) K pre 0,1 mol/l roztok KBr a (301 Ī 1) K pre 0,2 mol/l roztok KBr.
Tab. 8. Kompenzačné teploty Tc (K) pre látku XIX v 0,1 mol/l roztoku KBr a v 0,2 mol/l roztoku KBr 
Porovnanie vplyvu KCl (náplň ďalšej pripravovanej publikácie) s KBr ukazuje, že väčší objem aniónu Br- nepodporuje micelizaciu. Tieto poznatky sa dajú priamo využiť pri projekcii liekovej formy heptakaíniumchloridu ako potenciálneho lokálneho anestetika.
Na základe dosiahnutých výsledkov možno predpokladať, že heptakaíniumchlorid v prostredí vodného roztoku KBr vytvára micelovú štruktúru, znázornenú na obrázku 11. Z tejto schémy vyplýva, že hydrofilná časť heptakaíniumchloridu je v micele orientovaná do vodného prostredia, lipofilná časť vytvorí jadro micely.
Obr. 11. Micelová štruktúra heptakaíniumchloridu 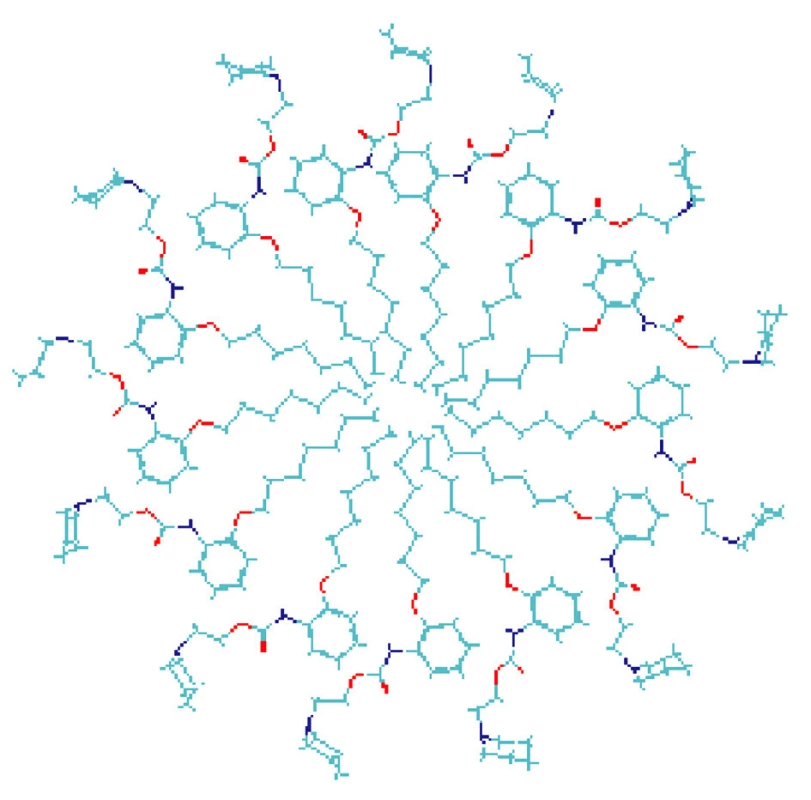
Táto práca je zahrnutá a vznikla v rámci projektu VEGA č. 1/4291/07.
Došlo 10. března 2008
Přijato 23. dubna 2008
Adresa pre korešpodenciu:
Mgr. Fils Andriamainty, PhD.
Odbojárov 10, 832 32 Bratislava, Slovenská republika
e-mail: mouanda@fpharm.uniba.sk
Zdroje
1. Fromherz, K.: Arch. Exp. Pathol. Pharmacol., 1914; 76, 257Đ302.
2. Švec, P., Béderová, B., Račanský, P. et al.: Farm. Obzor, 1978; 47, 543Đ554.
3. Čižmárik, J., Borovanský, A., Švec, P.: Acta Facult. Pharm. Univ. Comenianae, 1976; 29, 53Đ76.
4. Andriamainty, F., Čižmárik, J.: Farm. Obzor, 2004; 73, 100-102.
5. Andriamainty, F., Čižmárik, J., Holíková, M.: Sci. Pharm., 2004; 72, 221-225.
6. Andriamainty, F., Čižmárik, J., Zúdorová, Z. et al.: Pharmazie, 2007; 62, 77-78.
7. Evans, D. F., Wightmann, P. J.: J. Coll. Interf. Sci., 1982; 86, 515-524.
8. La Mesa, C.: J. Phys. Chem., 1990; 94, 323-326.
9. Kresheck, G. C., Hargraves, W. A.: J. Coll. Interf. Sci., 1974; 48, 481-493.
10. Lumry, R., Rajender, S.: Biopolymers., 1970; 9, 1125-1227.
11. Chen, L. J., Lin S. Y., Huang C. C.: J. Phys. Chem., 1998; 102, 4350-4356.
12. Ščukin, E. D., Percov, A. V., Amelinová, E. A.: Koloidn’ Chemie. 1. vyd‡n’. Praha, Academia, 1990, 303-333.
13. Andriamainty, F., Čižmárik, J.: Pharmazie, 1999; 54, 629-630.
14. Andriamainty, F., Čižmárik, J.: Pharmazie, 2003; 58, 440-441.
Štítky
Farmacie Farmakologie
Článek NOVÉ KNIHY
Článek vyšel v časopiseČeská a slovenská farmacie
Nejčtenější tento týden
2008 Číslo 3- Přerušovaný půst může mít významná zdravotní rizika
- Psilocybin je v Česku od 1. ledna 2026 schválený. Co to znamená v praxi?
- Biomarker NT-proBNP má v praxi široké využití. Usnadněte si jeho vyšetření POCT analyzátorem Afias 1
-
Všechny články tohoto čísla
- Biotická elicitace suspenzní kultury Trifolium pratense L.
- Vliv Mg-ATP na produkci flavonoidů v suspenzních kulturách Scutellaria baicalensis Georgii
- Syntéza alkylesterů kyseliny 2-{3-[4-(4-fluorfenyl)-piperazin-1-yl]-2-hydroxy-propoxy}-fenylkarbamové a in vitro hodnocení jejich β-antiadrenergní a vazodilatační aktivity
- Štúdium lokálnych anestetíkČasť 183: Micelizácia a termodynamické parametre heptakaíniumchloridu v prostredí roztoku KBr
- Léčivé přípravky v Mattioliho herbáři z roku 1596
- K obsahu národní části Českého lékopisu z pohledu přípravy léčivých přípravků v lékárnách
- X. sjezd české farmaceutické společnosti ČLS JEP
- XXX. pracovní dny sekce radiofarmacie české společnosti nukleární medicíny čls jep
- Slovenská farmaceutická spoločnosť 55 ročná
- Význačný farmaceut RNDr. PhMr. Lumír Jindra se dožil 80 let
- Docent Ing. Ivan Lacko je už sedemdesiatnikom
- Oslavy životního jubilea nestorů české farmacie
- NOVÉ KNIHY
- Česká a slovenská farmacie
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Léčivé přípravky v Mattioliho herbáři z roku 1596
- K obsahu národní části Českého lékopisu z pohledu přípravy léčivých přípravků v lékárnách
- XXX. pracovní dny sekce radiofarmacie české společnosti nukleární medicíny čls jep
- Štúdium lokálnych anestetíkČasť 183: Micelizácia a termodynamické parametre heptakaíniumchloridu v prostredí roztoku KBr
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Revma Focus: Spondyloartritidy
nový kurz
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání









