-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaMOŽNOSTI VYUŽITÍ ANALÝZY PŘEŽÍVÁNÍ V BIOMEDICÍNĚ A TECHNICE
MOŽNOSTI VYUŽITÍ ANALÝZY PŘEŽÍVÁNÍ V BIOMEDICÍNĚ A TECHNICE
The goal of this paper is to introduce a less known area of the statistics – survival analysis. The main feature of data files that are investigated using survival analysis methods is the fact, that they contain censored data besides the final data. The censored data arise when the time to occurrence of a given event at the object is observed and the event does not occur in the time of observation. We have only non-complete time data. In this paper there is described how it is possible to estimate and interpret the survival function, survival median and mean. The paper focuses on a comparison of two survival functions.
Keywords:
survival analysis, censored data, Kaplan-Meier curve, survival median and survival mean, log-rank test, generalized Wilcoxon test
Autoři: K. Langová
; J. Zapletalová; L. Ličman
Působiště autorů: Ústav lékařské biofyziky, Lékařská fakulta, Univerzita Palackého v Olomouci, ČR
Vyšlo v časopise: Lékař a technika - Clinician and Technology No. 1, 2013, 43, 5-10
Kategorie: Původní práce
Souhrn
Cílem tohoto článku je představit méně známou oblast statistiky – analýzu přežívání. Hlavním znakem datových souborů, které zkoumáme metodami analýzy přežívání, je skutečnost, že kromě konečných dat mohou obsahovat i data cenzorovaná. Cenzorovaná data vznikají, sledujeme-li u daného objektu dobu do výskytu dané události a k této události v době sledování nedojde, máme tedy k dispozici pouze neúplný časový údaj. V článku je popsáno, jak je možné odhadnout a interpretovat pravděpodobnostní funkci přežití, odhadnout medián přežívání a průměr přežívání. Pozornost je zaměřena na porovnání dvou funkcí přežití.
Klíčová slova:
analýza přežívání, cenzorovaná data, Kaplan-Meierova křivka, medián a průměr přežívání, log-rank test, obecný Wilcoxonův testÚvod
Statistika je vědní obor, jehož výsledky můžeme při své práci používat prakticky denně. Neexistuje snad jediný odborný medicínský časopis, ve kterém bychom nenašli články obsahující odbornou statistickou terminologii, a standardní statistické metody jsou většinou v povědomí lékařů a techniků známy. Cílem tohoto článku je představit méně známou oblast statistiky – analýzu přežívání. Metody analýzy přežívání je možné aplikovat na živé organismy i na poruchy technických zařízení. Hlavním znakem datových souborů, které zkoumáme metodami analýzy přežívání, je skutečnost, že kromě konečných dat mohou obsahovat i data cenzurovaná. Cenzorovaná (neúplná) data vznikají, sledujeme-li u daného objektu dobu do výskytu dané události a k této události v době sledování nedojde, máme tedy k dispozici pouze neúplný časový údaj. Událostí (event) se přitom rozumí výskyt libovolného definovaného jevu, chápaného ze subjektivního pohledu pozorovatele pozitivně, negativně nebo i neutrálně. I když je možno se v konkrétních případech setkat s různými názvy pro událost, často bývá označována jako selhání.
Materiál a metody
Cenzorovaná data
Obecně označuje termín analýza přežívání soubor statistických metod, které zpracovávají proměnnou čas do výskytu nějakého jevu (události), který se často nazývá též doba přežití. Časem nebo dobou přežití rozumíme počet let, měsíců, týdnů nebo dní od začátku sledování jedince až do výskytu jevu. Tento jev můžeme zvolit různě, jako příklady lze uvést úmrtí, incidenci onemocnění, návrat choroby, selhání transplantovaného orgánu nebo v oblasti techniky selhání určité součástky průmyslového zařízení (sledujeme dobu životnosti).
Většina studií zabývající se analýzou přežívání je v praxi ukončena dříve, než u všech pozorovaných objektů (osob) nastane sledovaná událost. Tuto situaci nazýváme v analýze přežívání cenzorováním. K cenzorování dochází tehdy, když je sledování objektu (např. pacienta) ukončeno dříve, než nastala sledovaná událost.
Cenzorování může nastat ze tří důvodů:
- sledovaná událost u objektu nenastane do konce studie,
- objekt je v průběhu sledování ze studie vyřazen nebo sám dobrovolně odstoupí,
- objekt je ztracen pro pozorování ještě před ukončením studie (např. pacient zemře a smrt není sledovanou událostí).
Po ukončení klinické studie získáme vstupní údaje pro následné statistické zpracování. Obvykle máme k dispozici soubor pacientů se sledovanou diagnózou. Soubor můžeme rozdělit do tří skupin:
- pacienti, u kterých nastala sledovaná událost (např. zemřeli) – konečná data
- pacienti, u kterých dosud nenastala sledovaná událost (např. žijí) – cenzorovaná data
- pacienti, kteří z nějakého důvodu byli vyřazeni ze studie nebo už prostě nemáme možnost je déle sledovat – rovněž cenzorovaná data.
U každého pacienta máme tedy dva údaje:
- dobu sledování a
- důvod ukončení sledování, který kódujeme číslem 1 pro případ, kdy sledovaná událost nastala (skupina 1) a číslem 0 pro případ, kdy sledovaná událost nenastala (skupina 2 nebo 3).
Cílem analýzy přežívání je
- odhadnout a interpretovat pravděpodobnostní funkci přežití a rizikovou funkci
- odhadnout medián přežívání a průměr přežívání
- porovnat funkce přežití v případě, že studie pracuje s více skupinami pacientů
- analyzovat vztah mezi sledovanými vysvětlujícími proměnnými a dobou přežití.
V článku se budeme zabývat pouze odhadem funkce přežití, mediánu a průměru přežívání a porovnáním více funkcí přežití.
Odhad a interpretace funkce přežití
Jedním z hlavních cílů analýzy přežívání je odhad-nout funkci přežití S(t). Funkce přežití udává pravděpodobnost, že osoba žije déle než konkrétně specifikovaný čas t. S(t) = P(T > t), kde T je nezáporná náhodná veličina, která vyjadřuje dobu uplynulou od zahájení pozorování jedince do výskytu sledovaného jevu (Obr. 2). V praxi se funkce přežití odhaduje metodou Kaplana a Meiera. V textu budeme symbolem S(t) značit teoretickou funkci přežití platnou pro celou populaci a symbolem Ŝ(t) funkci přežití pro konkrétní soubor sledovaný studií. Hodnoty funkce Ŝ(t) se počítají ve všech časech tj, kdy došlo u alespoň jednoho z pacientů ke sledovanému jevu, tedy pro všechna konečná data. Výpočet vychází z teorie pravděpodobnosti a je založen na relativních četnostech.
Obr. 1. Grafické znázornění přežívání pěti pacientů, kteří vstoupili do studie v různých časových okamžicích. Nahoře skutečný kalendářní čas, dole doba od vstupu do studie. 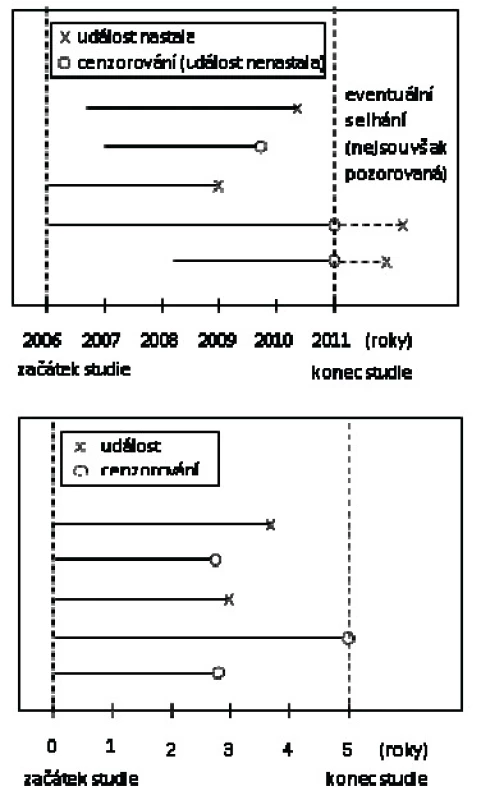
Obr. 2. Teoretický tvar funkce přežití. 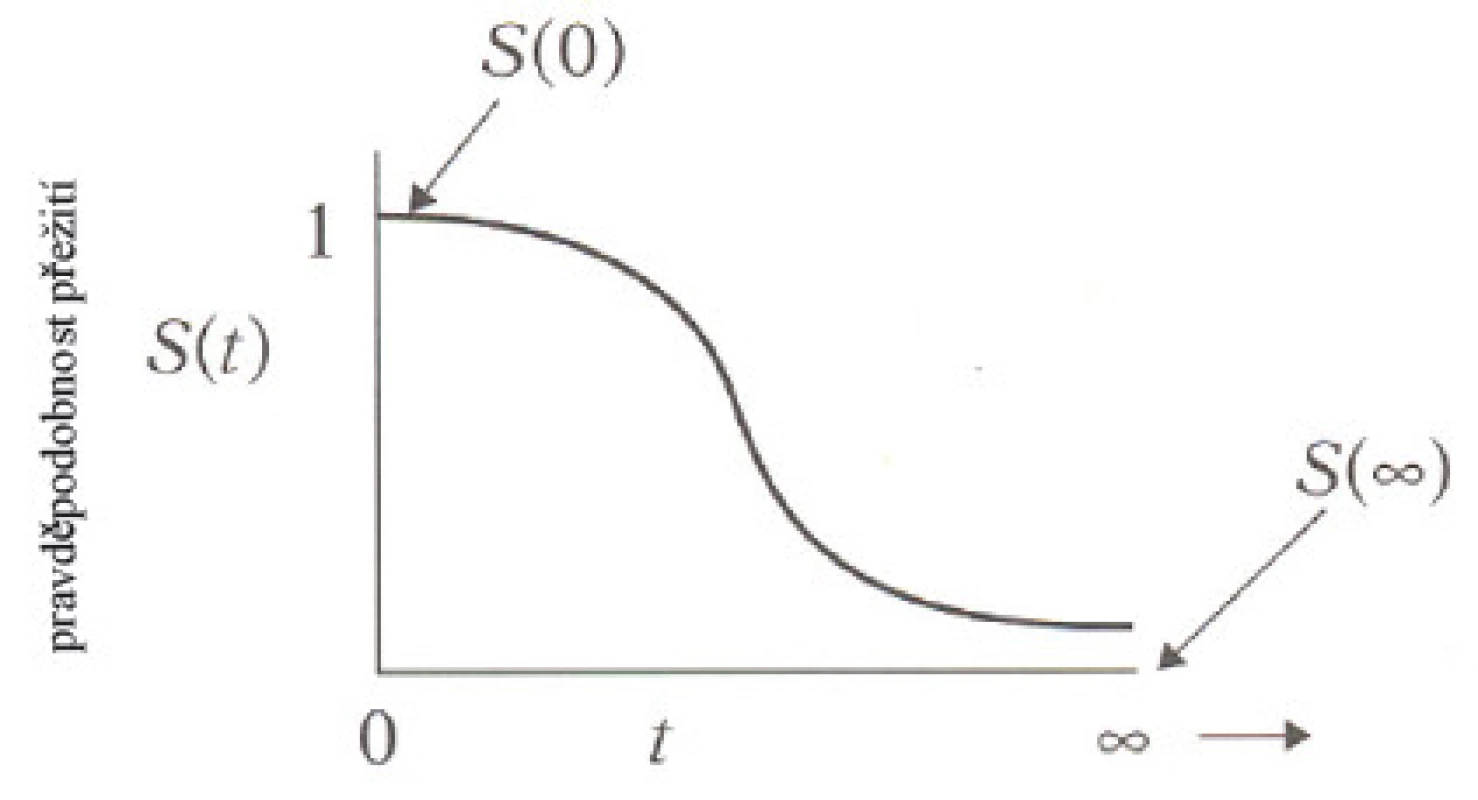
Kaplan-Meierův odhad funkce přežití v čase tj je definován následovně:
Skutečný tvar funkce přežití pro soubor sledovaný studií je znázorněn na obrázku 3. Na vodorovné ose je zaznamenán čas (tj. doba do výskytu sledované události ve dnech, týdnech, měsících nebo letech), na svislé ose pravděpodobnost přežití tohoto času, která nabývá hodnot od nuly do jedné. Funkce je schodovitá, každá událost (např. úmrtí) způsobí pokles pravděpodobnosti přežití (schod). Značky (svislé čárky) v grafu značí cenzorovaná (neúplná) data. Jinými slovy výskyt sledované události (např. úmrtí pacienta) vede ke snížení pavděpodobnosti přežití zbývajících subjektů.
Obr. 3. Skutečný tvar funkce přežití, Ŝ(t). 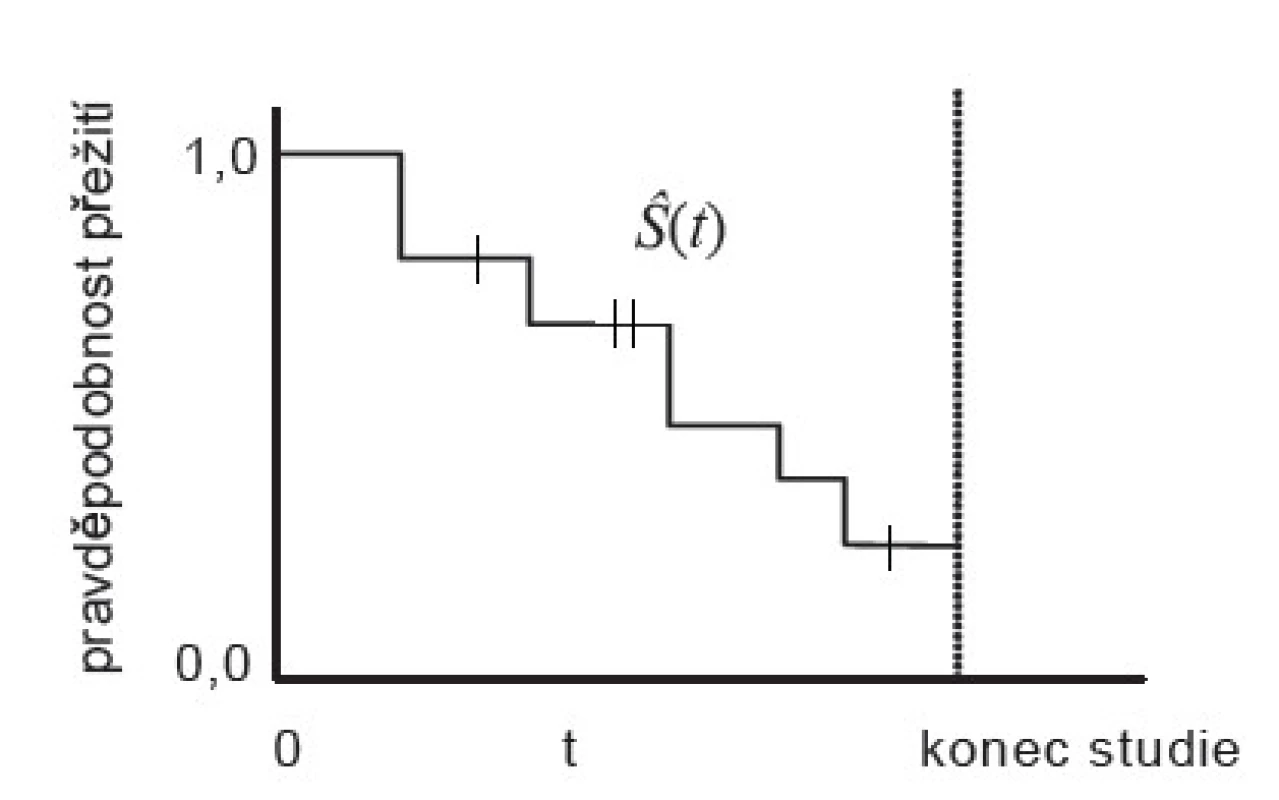
Protože interval sledování klinické studie není nikdy nekonečný, je možné a v praxi časté, že sledovaná událost nenastane u všech pacientů a odhadovaná pravděpodobnost přežití neklesne na konci studie až k nule.
Postup odhadu Kaplan-Meierovy funkce přežití vysvětlíme na modelovém příkladu.
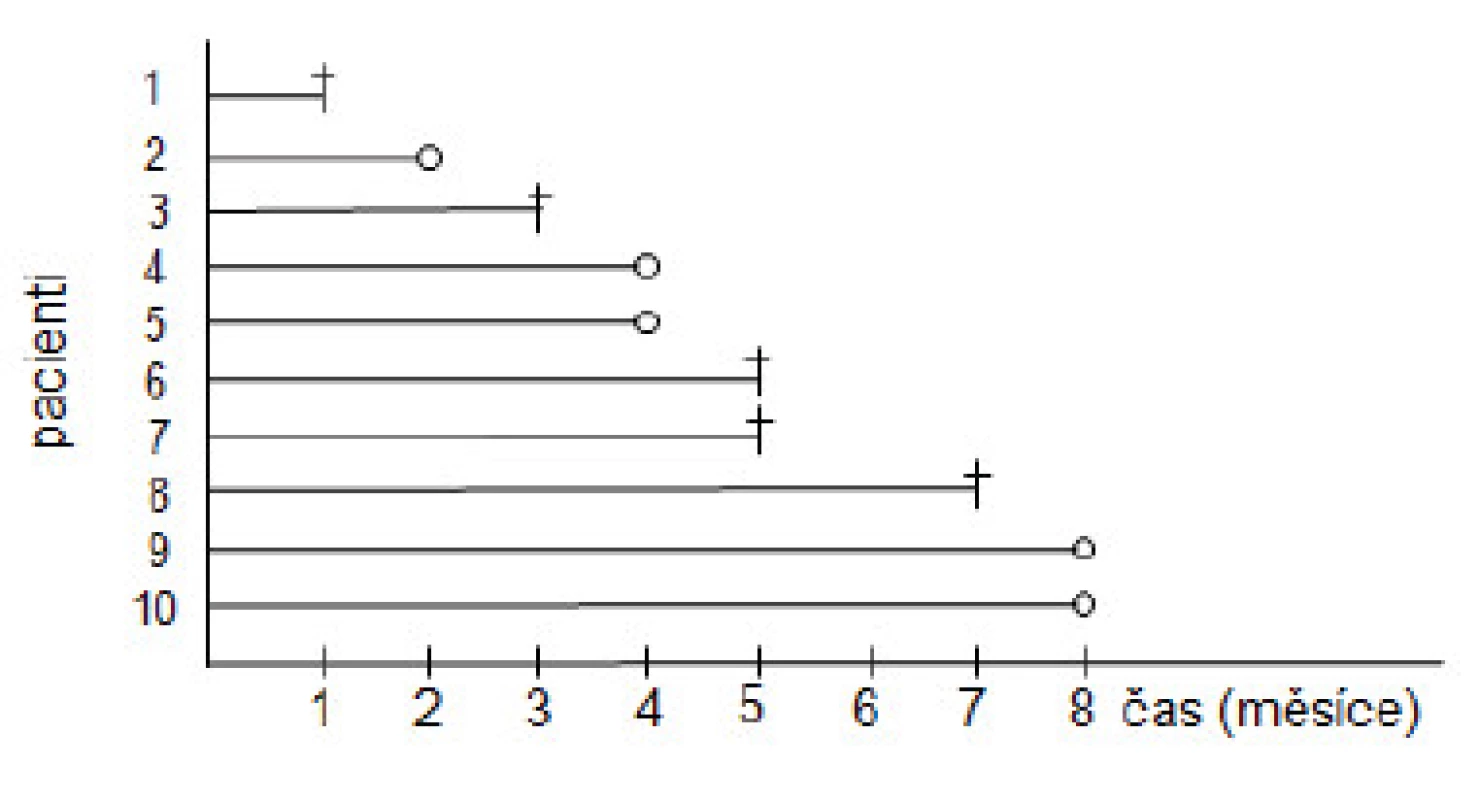
Na obrázku 4 jsou znázorněny údaje o 10 pacientech seřazené podle délky sledování (křížek značí výskyt sledované události např. úmrtí, kroužek je symbol pro cenzorovaný údaj).
V čase Ŝ(t0) = 0 je pravděpodobnost přežití rovna 1. V čase t1 = 1 umírá první pacient, pravděpodobnost přežití tohoto časového okamžiku je 9/10. Dle vzorce (1) dostáváme:
V čase t2 = 2 žádná událost nenastala, pravděpodobnost přežití tohoto časového okamžiku je tedy stejná 0,9.
V čase t3 = 3 sledujeme už jen 8 pacientů a jeden pacient umírá. Přirozeným odhadem přežití 3. měsíce je 7/8, ale pouze pro pacienty, kteří se dožili 3. měsíce. Pro celkový odhad musíme násobit 7/8 pravděpodobností přežití 2. měsíce, tedy:
V čase t4 = 4 žádná událost nenastala, pravděpodobnost přežití tohoto časového okamžiku je tedy stejná 0,788. V čase t5 = 5 sledujeme 5 pacientů a dva pacienti umírají.
V čase t6 = 6 žádná událost nenastala, pravděpodobnost přežití tohoto časového okamžiku je tedy stejná 0,473. V čase t7 = 7 sledujeme 3 pacienty a jeden pacient umírá.
V čase t8 = 8 žádná událost nenastala, pravděpodobnost přežití tohoto časového okamžiku je tedy stejná 0,315.
Z vypočítaných hodnot funkce přežití můžeme funkci sestrojit (obr. 5), cenzorované údaje jsou znázorněny pomocí krátkých úseček.
Obr. 5. Kaplan-Meierův odhad funkce přežití. 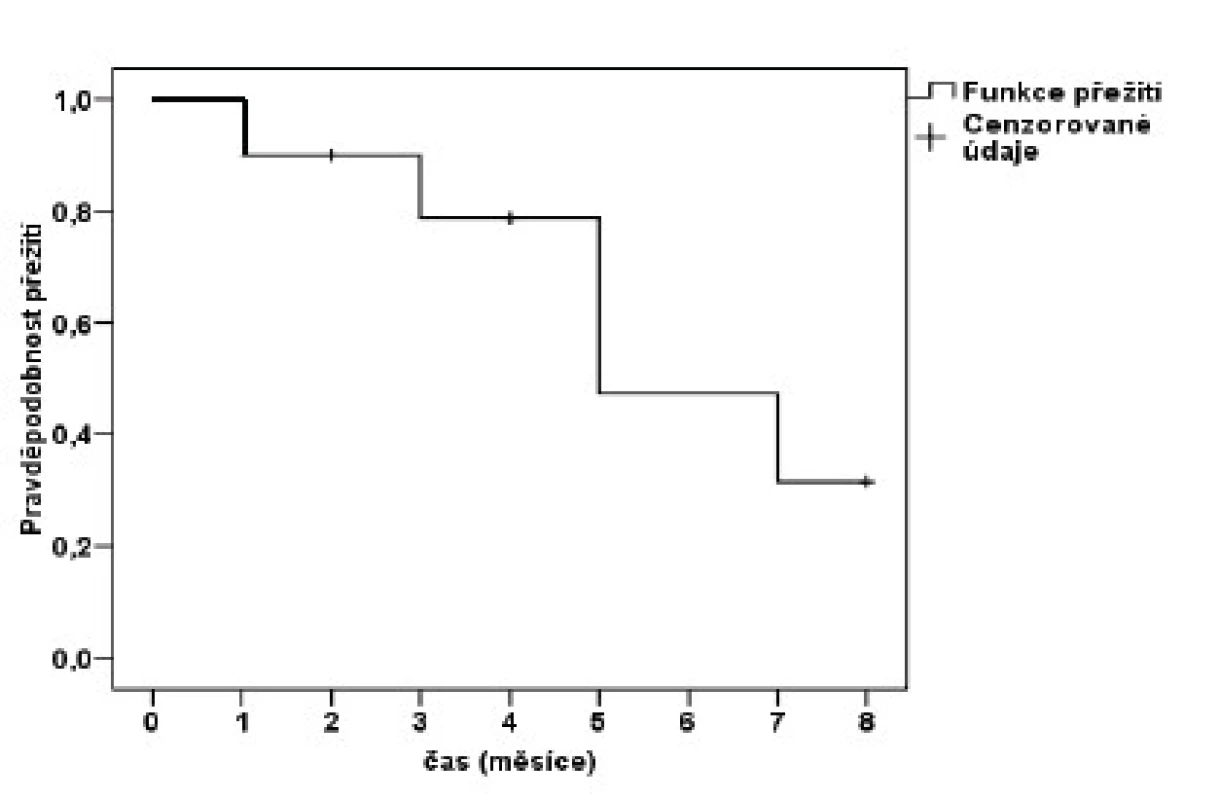
Odhad a interpretace mediánu a průměru přežívání
V analýze přežívání jsou důležitými údaji medián přežívání a průměrné přežívání.
Medián přežití je časový údaj, ve kterém je pravděpodobnost přežití rovna 0,5.
Průměrná doba přežívání se definuje jako plocha pod křivkou přežití. Pokud tedy soubor dat obsahuje cenzorovaná data, nelze pro výpočet mediánu a průměru použít klasické postupy známé z popisné statistiky pro konečná data.
Jestliže by při práci se souborem dat, který obsahuje i cenzorované údaje, byl výpočet průměru a mediánu proveden klasickým způsobem, znamenalo by to, že všechna data jsou konečná, tedy že u všech subjektů došlo ke sledované události.
V takovém případě by odhad průměru i mediánu byl nižší než při použití správného postupu, při kterém je rozlišováno, zda u daného objektu došlo k události či nikoliv.
V tabulce 1a jsou zadány časy přežití 12 pacientů, ve sloupci status je kódováno, zda u pacienta nastala (=1) sledovaná událost či nenastala (=0). Tvar Kaplan-Meierovy křivky přežití s vyznačenou hodnotou mediánu je znázorněn na obrázku 6. Plocha pod křivkou přežití odpovídá průměrné hodnotě přežívání. Výpočet průměru a mediánu přežívání pomocí statistického programu SPSS i se standardní chybou odhadu (SE) a 95% intervalem spolehlivosti (95% CI) je ukázán v tabulce 1b.
Obr. 6. Kaplan-Meierova křivka přežití pro data z tab. 1a se znázorněnou hodnotou mediánu přežití. 
Tab. 1a: Příklad souboru dat, který obsahuje konečné i cenzorované údaje. 
Tab. 1b: Výpočet průměru a mediánu přežívání pro data z tab. 1a pomocí statistického software SPSS. 
Pokud by se s daty pracovalo pomocí klasických metod popisné statistiky, znamenalo by to, že všem objektům je přiřazen status 1 (tab. 2a), tvar Kaplan-Meierovy křivky (obr. 7) i odhady průměru a mediánu přežití (tab. 2b) by byly jiné.
Obr. 7. Kaplan-Meierova křivka přežití pro data z tab. 2a se znázorněnou hodnotou mediánu přežití. 
Tab. 2a: Příklad souboru dat, který obsahuje chybně pouze konečné údaje (tj. cenzorované údaje jsou považovány za konečné). 
Tab. 2b: Výpočet průměru a mediánu přežívání pro data z tab. 1a pomocí statistického software SPSS. 
Běžným problémem v klinických studiích je srovnání dvou nebo více typů léčby z hlediska jejich schopnosti prodloužit život pacientů nebo udržet pacienty v remisi. Vyvstává tedy problém porovnat dvě nebo více křivek přežití. Pro toto srovnání existuje několik statistických testů. Nejpoužívanější jsou log-rank test a obecný Wilcoxonův test. Tyto testy nám odpovídají na otázku, zda jsou Kaplan-Meierovy křivky statisticky ekvivalentní.
Log-rank test je v podstatě chí-kvadrát test pro velký výběr. Log-rank statistika porovnává pozorovaný počet jevů v každém časovém okamžiku, kdy došlo ke sledovanému jevu, s očekávaným počtem za platnosti nulové hypotézy, která předpokládá, že porovnávané křivky přežití se neliší.
Obecný Wilcoxonův test nepracuje s konkrétními časy do výskytu sledovaného jevu, ale pouze s pořadím výskytu událostí a cenzorováním v jednotlivých souborech. Každý takto uspořádaný údaj v jednom souboru se porovnává se všemi upořádanými údaji ve druhém souboru. Tím vyloučíme vliv extrémních časových údajů ve vstupních souborech.
Je-li dosažená hladina signifikance příslušného testu menší než 0,05, považujeme posuzované typy léčení za rozdílné z hlediska jejich schopnosti prodloužit život pacientů.
Zabýváme-li se otázkou, kdy použít log rank test a kdy použít Wilcoxonův test, je třeba vědět, že hlavní rozdíl mezi testy je v tom, jakou kladou během doby přežití váhu na jednotlivé události. Log-rank test klade během doby sledování na všechny události stejnou váhu. Wilcoxonův test se od předchozího liší tím, že čím je doba pozorování delší, tím dává menší váhu rozdílům mezi pozorovaným a očekávaným počtem sledovaných událostí. Jednoduchou pomůckou, jak zjistit, který z testů použít, je vykreslit si obě funkce přežití pro jednotlivé skupiny do jednoho grafu a podle jejich průběhu vybrat vhodnější test. Pokud se například tyto dvě funkce kříží (obr. 8), je vhodnější zvolit k testování Wilcoxonův test. Pokud se funkce nekříží, je lepší zvolit k testování, zda jsou funkce přežití pro jednotlivé skupiny rozdílné či nikoliv, log-rank test. Křivky přežití, které jsou znázorněny na obrázku 8, byly porovnány pomocí statistického software SPSS dvěma statistickými testy log-rank testem a Wilcoxonovým testem (tab. 3).
Obr. 8. Funkce přežití pro dvě skupiny pacientů léčených dvěma terapiemi. 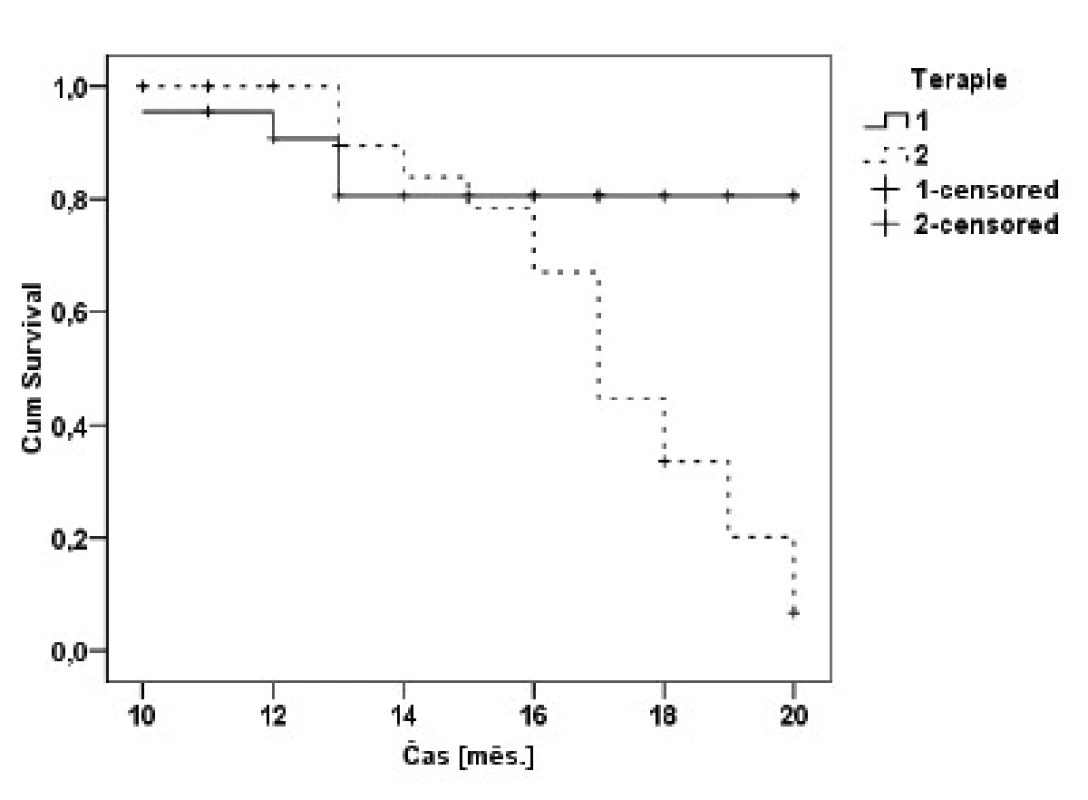
Tab. 3: Výsledek dvou statistických testů, výstup z programu SPSS. 
Z tabulky 3 je zřejmé, že dosažená hladina signifikance 0,008 u log-rank testu je nižší než obecně uvažovaná hladina α = 0,05, výsledek bychom tedy mohli považovat za statisticky významný a rozdíly v přežívání pacientů léčených dvěma terapiemi za sku-tečné. Naopak dosažená hladina signifikance u Wilcoxonova testu je 0,116, v tomto případě by byl výsledek považován za statisticky nevýznamný. Použijeme-li pomůcku o křížení křivek přežití, rozhodneme se použít Wilcoxonův test.
Diskuse
Na příkladech bylo ukázáno, jak je možné špatně interpretovat výsledky statistického šetření, pokud je použita nevhodná metoda. V případě výpočtu průměru a mediánu u souboru dat, ve kterém jsou obsaženy i cenzorované údaje, dochází k podhodnocení odhadu obou statistik. Hodnoty průměru i mediánu vycházejí nižší ve srovnání s hodnotami, které dostaneme, pokud správně aplikujeme metody analýzy přežívání.
Při porovnání funkcí přežívání statistickými testy, je třeba zvolit vhodný test. Pokud se nezamýšlíme nad volbou správného testu a vybereme například první možnost, kterou nám statistický software nabízí, může take dojít k chybné interpretaci závěrů statistického zpracování.
Závěr
Při statistickém zpracování dat je třeba zvážit charakter dat a zvolit správnou statistickou metodu. Kromě klasických statistických metod, které pracují s konečnými daty, existují také metody analýzy přežívání, které berou do úvahy skutečnost, že informace u všech subjektů nejsou úplné. Při nevhodně zvolené metodě může dojít ke špatné interpretaci výsledků statistického zpracování.
Poděkování
Tato práce byla zpracována za podpory projektu CZ.1.07/2.4.00/17.0058 Prohloubení odborné spolupráce a propojení ústavů lékařské biofyziky na lékařských fakultách a projektu CZ.1.05/2.1.00/01.0030.
Kateřina Langová, Ph.D.
Ústav lékařské biofyziky,
Lékařská fakulta
Univerzita Palackého v Olomouci
Hněvotínská 3, CZ-775 15 Olomouc
E-mail: langova@tunw.upol.cz
Tel.:+420 585 632 120
Zdroje
[1] Akritas G. Michael: Nonparametric Survival Analysis, Statistical Science, 2004, vol. 19, no. 4, p. 615–623.
[2] Alling D. Early decision in the Wilcoxon two-sample test. J. Amer. Statist. Ass. 1963; vol. 58, p. 713–20.
[3] Altman D. G. Practical statistics for medical research.
Chapman & Hall, UK 1995.
[4] Anděl J. Matematická statistika. SNTL – Nakladatelství technické literatury, Praha, 1985.
[5] Gehan, E. A. Statistical methods for survival time studies. In: Cancer Therapy: Prognostic Factors and Criteria, M. J. Staquet, eds. New York: Raven Press; 1975.
[6] Kalbfleisch, J. D., Prentice P.L. The statistical analysis of failure time data. New York: John Wiley & Sons, Inc., 1980.
[7] Kaplan E. L., Meier P. Nonparametric estimation from incomplete observations. J Amer Statist Ass, 1958, vol. 53, p. 457–481.
[8] Klein J. P., Goel P. K. Survival Analysis: State of the Art. Kluwer Academic Publisher, Dordrecht, The Netherlands, 1992.
[9] Klein J. P., Moeschberger M. L. Survival Analysis: Techniques for Censored and Truncated Data. Springer, New York, USA, 1997.
[10] Kleinbaum G. David, Klein Mitchel: Survival Analysis, A Self–Learning Text, Springer New York, 2005.
[11] Langová K.: Survival analysis for clinical studies, Biomed Pap Med Fac Univ Palacky, 2008, vol. 52, no.2, p. 303-307.
[12] Lawless R. F. Statistical models and methods for lifetime data. John Wiley & Sons, Inc., New York , USA, 1982.
[13] Zheng Z. Two methods of estimating the mean survival time from censored samples. The Indian Journal os Statistics, 1995, vol. 57, no. 1, p. 126-136.
Štítky
Biomedicína
Článek vyšel v časopiseLékař a technika

2013 Číslo 1-
Všechny články tohoto čísla
- SROVNÁNÍ RŮZNÝCH PŘÍSTUPŮ HRANOVÉ DETEKCE KONČETINOVÝCH TEPEN V PODÉLNÉM ŘEZU ULTRAZVUKOVÉHO OBRAZU
- IMUNOFLUORESCENČNÍ ANALÝZA PROAPOPTICKÝCH SIGNÁLNÍCH MOLEKUL V BUŇKÁCH LIDSKÉHO MELANOMU PO FOTODYNAMICKÉ TERAPII
- Fototoxický vliv porfyrinových sensitizerů a viditelného záření na gram-pozitivní methicilin-rezistentní kmen S. aureus
- 13C-methacetinový dechový test u pacientů s jaterní cirhózou a dekompenzovaným srdečním selháním
- Testing of automatized rehabilitation device designed for elderly by industrial robot
- Specific behaviour of the blood sedimentation processes examined by the electrochemical impedance microsensor
- Development of biomedical information systems: MSL concept of e-learning – pilot study results
- MOŽNOSTI VYUŽITÍ ANALÝZY PŘEŽÍVÁNÍ V BIOMEDICÍNĚ A TECHNICE
- Lékař a technika
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- MOŽNOSTI VYUŽITÍ ANALÝZY PŘEŽÍVÁNÍ V BIOMEDICÍNĚ A TECHNICE
- 13C-methacetinový dechový test u pacientů s jaterní cirhózou a dekompenzovaným srdečním selháním
- Fototoxický vliv porfyrinových sensitizerů a viditelného záření na gram-pozitivní methicilin-rezistentní kmen S. aureus
- SROVNÁNÍ RŮZNÝCH PŘÍSTUPŮ HRANOVÉ DETEKCE KONČETINOVÝCH TEPEN V PODÉLNÉM ŘEZU ULTRAZVUKOVÉHO OBRAZU
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Revma Focus: Spondyloartritidy
nový kurz
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání