NEW METHOD FOR ESTIMATION OF FLUENCE COMPLEXITY IN IMRT FIELDS
Intensity modulated radiation therapy (IMRT) planning and verification is a complex process but it could be simplified without compromising patient safety. One such way is suggested in our work. A new method for estimation of fluence complexity in IMRT fields is proposed. Unlike other previously published works, it is based on portal images calculated by the Portal Dose Calculation algorithm in Eclipse (version 8.6, Varian Medical Systems) in the plane of the EPID aS500 detector. Fluence complexity is given by the number and the amplitudes of dose gradients in these matrices. Our method is validated using a set of clinical plans where fluence has been smoothed manually so that each plan has a different level of complexity. Fluence complexity calculated with our tool is in accordance with the different levels of smoothing and correlates well with dose volume histogram parameters. Thus, it is possible to estimate plan complexity before carrying out the measurement, which could save time in the replanning and remeasuring process.
Keywords:
fluence complexity, IMRT verification, gamma analysis, radiotherapy
Authors:
Tereza Hanušová 1,2; Vladimír Vondráček 1,3; Klára Badraoui Čuprová 3; Ivana Horáková 4; Irena Koniarová 1,4
Authors place of work:
Department of Dosimetry and Application of Ionizing Radiation, Faculty of Nuclear Sciences and Physical Engineering, Czech Technical University in Prague, Praha, Czech Republic
1; Hospital Na Bulovce, Praha, Czech Republic
2; Proton Therapy Center Czech, Praha, Czech Republic
3; National Radiation Protection Institute, Praha, Czech Republic
4
Published in the journal:
Lékař a technika - Clinician and Technology No. 1, 2016, 46, 29-32
Category:
Původní práce
Summary
Intensity modulated radiation therapy (IMRT) planning and verification is a complex process but it could be simplified without compromising patient safety. One such way is suggested in our work. A new method for estimation of fluence complexity in IMRT fields is proposed. Unlike other previously published works, it is based on portal images calculated by the Portal Dose Calculation algorithm in Eclipse (version 8.6, Varian Medical Systems) in the plane of the EPID aS500 detector. Fluence complexity is given by the number and the amplitudes of dose gradients in these matrices. Our method is validated using a set of clinical plans where fluence has been smoothed manually so that each plan has a different level of complexity. Fluence complexity calculated with our tool is in accordance with the different levels of smoothing and correlates well with dose volume histogram parameters. Thus, it is possible to estimate plan complexity before carrying out the measurement, which could save time in the replanning and remeasuring process.
Keywords:
fluence complexity, IMRT verification, gamma analysis, radiotherapy
Introduction
Intensity modulated radiation therapy (IMRT) helps to avoid organs at risk in proximity of the tumor and thus allows to increase prescribed dose compared to 3D conformal radiotherapy. Because the technique is quite complex, clinics that are not confident with their implementation of IMRT still verify each patient’s plan prior to treatment. As IMRT is indicated in an increasing number of cases, this process might soon be inapplicable. The question is how to reduce time needed for verification without compromising patient safety. According to the authors, one solution is to avoid production of overly modulated fields that do not further improve plan quality by recognizing excess plan complexity on the planning stage, and thus avoid complete replanning and remeasurement of the plan. Furthermore, overly modulated fields not only prolong the process of verification, they can also cause errors during dynamic treatment that had not been detected, as they require complicated leaf motion. Used components that are ready to be replaced (e. g. leaf motors) might compromise dose delivery precision at the time of treatment, which was not the case at the time of verification. A method for fluence complexity calculation is proposed here which can help to distinguish between adequately and inadequately complex IMRT fields or plans at the planning stage.
Works that have been published so far calculate fluence complexity in an IMRT field using plan parameters such as the optimal fluence estimated by the treatment planning system (TPS) or the number of monitor units (MU). The most frequently used parameters are probably the modulation index [1, 2] and the modulation complexity score [3]. Other parameters are described in several papers [4, 5, 6]. Recently, another promising solution has been proposed by Nauta et al. [7] using fractal analysis. However, none of them has widely been used in the clinical environment. Therefore, we propose a different approach that could easily be implemented into treatment planning systems and that could be more directly correlated to results of verification.
Materials and Methods
Fluence complexity calculation
Here, fluence complexity is defined using the number and the amplitude of dose gradients in matrices of dose distribution calculated by the Portal Dose Calculation algorithm (PDC) in Eclipse (version 8.6, Varian Medical Systems, Palo Alto, USA) in the plane of the electronic portal imaging device (EPID) when creating a verification plan. Mathematically, the quantity can be defined as
where Pq is the number and Vq is the sum of amplitudes of dose gradients in the matrix mentioned above which are greater than a certain limit q, m and n are the matrix dimensions and cijφ is the amplitude of the dose gradient on the position [i, j] in the direction φ. There are 8 directions for each point of the matrix as illustrated in Fig. 1. (Implementation of the algorithm takes account of the matrix edges.)

The amplitude cijφ is calculated as the difference between values in adjacent pixels divided by the real distance between measuring points of the detector. The value of q was chosen to be 400 arbitrary units (values in the predicted matrix of dose distribution which is then exported in DICOM format from the TPS Eclipse are relatively proportional to dose; however, no physical quantity can be assigned to them), based on histograms showing the number of different dose gradient amplitudes in the IMRT fields considered. This is a way to exclude small dose gradients that are present outside the actual treatment field, because the PDC algorithm calculates dose distribution in the entire sensitive area of the EPID detector.
Even if dose distribution is used for calculation, the term fluence complexity is used here, supposing that these two physical quantities are correlated. If fluence complexity in an IMRT field is changed at the planning stage, dose complexity in the distribution perpendicular to the beam central axis should change accordingly.
Matrices of dose distribution predicted in the plane of the detector EPID were exported in DICOM format from the TPS Eclipse. MATLAB (The Mathworks, Inc., USA) was used to calculate fluence complexity. The experiment was carried out with EPID aS500 and Varian CLINAC 600C/D as well as Varian CLINAC 2100C/D (Varian Medical Systems, Palo Alto, USA).
Evaluation of the method
The method was evaluated using clinical IMRT plans that were further modified. Six patients with different diagnoses (head-and-neck, pelvis, pancreas) and different photon energies (6 MV, 18 MV) were included. Plan 1 was the original patient’s plan. Plan 2 was a modification of plan 1 – manual smoothing of field fluences was applied, using the tools available in Eclipse, as is normally done during the planning process at our institute, Hospital Na Bulovce. Fluences were further modified in plan 3 and plan 4. Finally, 4 plans with different levels of smoothing were obtained for each patient.
Verification plans to be measured with the EPID detector were then created for all plans and fluence complexity was calculated using our method. For each plan the average sum of dose gradient amplitudes in a field and the average number of dose gradients in a field was estimated, averaging out all fields in each plan. These two parameters were used as the measure of plan complexity.
Dose volume histogram (DVH) parameters for structures of interest were also evaluated for all plans.
Results and Discussion
The calculated plan complexity agreed with the manual level of smoothing in all cases, as can be seen in Fig. 3. The manual level of smoothing, and consequently also the calculated plan complexity, agreed with the total number of MU in a plan, this parameter being often used for comparison in literature. This is illustrated in Fig. 2.


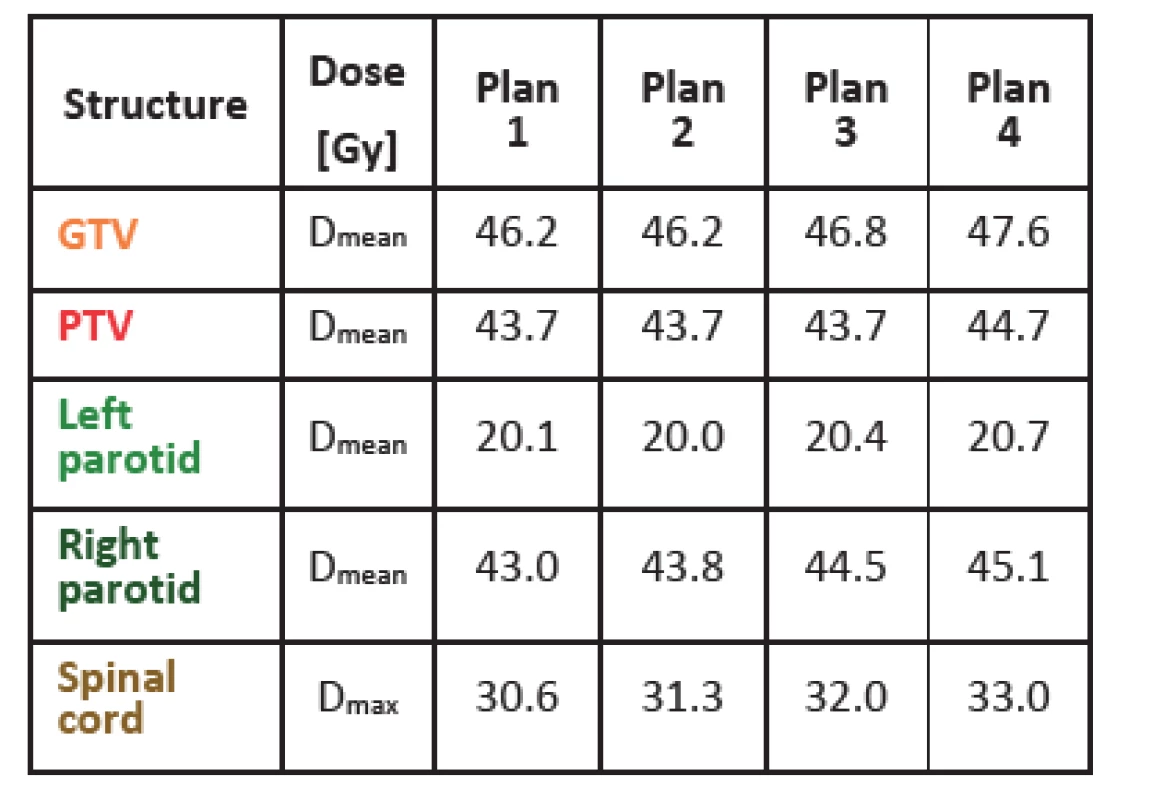
Tab. 1 shows dose values for gross tumor volume (GTV), planning target volume (PTV) and several organs at risk for one of the patients studied (a head-and-neck case). As fluences get smoother, the mean dose and the maximal dose in all structures gets higher. This might be due to the fact that with smoother fluences it is more difficult to avoid organs at risk but at the same time it is easier to achieve more homogenous dose in tumor (higher mean dose). For the other five cases, results were similar with just a few exceptions, like the mean dose for left parotid shown in Tab. 1, where the mean dose is slightly higher in plan 1 than in plan 2. With the method of fluence smoothing used, it is difficult to achieve more markedly distinct results. Anyhow, dose values are distinctly different when comparing plan 1 and plan 4. In general, it can be concluded that as fluences get more complex, lower doses can be achieved in organs at risk. However, this means a less homogenous dose distribution and lower mean dose in tumor, as can be naturally expected.
Conclusions
A new method for fluence complexity calculation in IMRT fields has been proposed. It differs in principle from other methods published so far. Evaluation of our tool with six IMRT cases showed agreement between the level of manual smoothing of field fluences, fluence complexity calculation with our tool, total number of MU in plan and DVH parameters for tumor and organs at risk. Estimation of fluence complexity prior to plan verification could help to recognize overly modulated fields or plans and save time avoiding reoptimization and remeasurement. It could also help to reduce potential leaf positioning errors during dynamic treatment by excluding inadequately modulated fields from clinical use. However, the level of fluence complexity is systematically different for different patients. This might depend on many factors, like the treatment site, shape of tumor, position of organs at risk, etc. Therefore, further investigations need to be done to estimate appropriate thresholds in order to recognize overmodulation. Individual fields could be taken into account instead of average value for a plan. Correlation of fluence complexity and results of measurement or other means of verification should also be determined.
Acknowledgement
The work has been supported by student research grant No. SGS15/217/OHK4/3T/14.
Ing. Tereza Hanušová
Katedra dozimetrie a aplikace ionizujícího záření
Fakulta jaderná a fyzikálně inženýrská
České vysoké učení technické v Praze
Břehová 7,
CZ-115 19 Praha 1
E-mail: tereza.hanusova@fjfi.cvut.cz
Phone: +224 358 364
Zdroje
[1] Webb, S. Use of a quantitative index of beam modulation to characterize dose conformality: illustration by a comparison of full beamlet IMRT, few-segment IMRT (fsIMRT) and conformal unmodulated radiotherapy. Phys. Med. Biol, 2003, vol. 48, no. 14, p. 2051–2062.
[2] Nicolini, G., Fogliata, A., Vanetti, E., Clivio, A., Ammazzalorso, F., Cozzi, L. What is an acceptably smoothed fluence? Dosimetric and delivery considerations for dynamic sliding window IMRT. Radiat. Oncol., 2007, vol. 42, no. 2, p. 42–54.
[3] McNiven, A. L., Sharpe, M. B., Purdie T. G. A new metric for assessing IMRT modulation complexity and plan deliverability. Med. Phys., 2010, vol. 37, no. 2, p. 505–515.
[4] Mohan, R., Arnfield, M., Tong, S., Wu, Q., Siebers, J. The impact of fluctuations in intensity patterns on the number of monitor units and the quality and accuracy of intensity modulated radiotherapy. Med. Phys., 2000, vol. 27, no. 6, p. 1226–1237.
[5] Llacer, J., Solberg, T. D., Promberger, C. Comparative behaviour of the Dynamically Penalized Likelihood algorithm in inverse radiation therapy planning. Phys. Med. Biol., 2001, vol. 46, no. 10, p. 2637–2663.
[6] Coselmon, M. M., Moran, J. M., Radawski, J. D., Fraass, B. A. Improving IMRT delivery efficiency using intensity limits during inverse planning. Med. Phys., 2005, vol. 32, no. 5, p. 1234–1245.
[7] Nauta, M., Villarreal-Barajas, J. E., Tambasco, M. Fractal analysis for assessing the level of modulation of IMRT fields. Med. Phys., 2011, vol. 38, no. 10, p. 5385-5393.
Štítky
BiomedicínaČlánek vyšel v časopise
Lékař a technika

2016 Číslo 1
Nejčtenější v tomto čísle
- The viability of ovarian carcinoma cells A2780 affected by titanium dioxide nanoparticles and low ultrasound intensity
- Raman label-free visualisation of Titanium dioxide nanoparticles uptake in BJ cell LINES
- Optical nerve segmentation using The Active shape method
- NEW METHOD FOR ESTIMATION OF FLUENCE COMPLEXITY IN IMRT FIELDS


