-
Články
- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
COMPARISON OF DOSE CALCULATION ALGORITHMS FOR LEKSELL GAMMA KNIFE PERFEXION USING MONTE CARLO VOXEL PHANTOMS
Dose calculation algorithms implemented in the treatment planning software for Leksell Gamma Knife differ in their results, especially in the areas of steep electron density gradients. The Tissue Maximum Ratio (TMR) algorithm (in two variants) does not employ any patient-specific data besides the idealized skull shape, while the Convolution algorithm takes full advantage of voxel data from computed tomography (CT) to create a more faithful description of the anatomy.
The presented Monte Carlo model of Leksell Gamma Knife Perfexion was created in order to investigate dose distribution characteristics of the machine and to verify the mentioned algorithms. It builds upon Geant4 (a simulation toolkit for particle passage in matter) and being designed in a modular fashion, it enables to put several geometry components together at runtime. A precise description of the Perfexion collimation system is supplemented by voxel phantoms constructed from CT images in the DICOM format.
As a preliminary study, three specific plans of varying complexity were exported from the treatment planning software – a phantom for gel dosimetry and two clinical cases – and simulated using the Monte Carlo model. Scoring volumes were defined so that a direct dose distribution comparison could be made using three-dimensional gamma index analysis. All results show good agreement between the Monte Carlo method and calculated distributions with no significant difference between the algorithms (with over 99.9 % points satisfying the criteria ΔDM = 0,03 and Δdm = 1 mm). We plan to make further studies with more specific, artificially designed treatment plans in order to assess the subtle differences between the algorithms.Keywords:
gamma knife; Perfexion; voxel phantoms; Geant4; treatment planning
Authors: Jan Pipek 1; Josef Novotný Jr. 1,2,3; Josef Novotný 1; Petra Kozubíková 1
Authors place of work: Faculty of Nuclear Sciences and Physical Engineering, Czech Technical University in Prague, Prague, Czech Republic 1; Department of Medical Physics, Na Homolce Hospital, Prague, Czech Republic 2; Department of Radiation Oncology, University Hospital Motol, Prague, Czech Republic 3
Published in the journal: Lékař a technika - Clinician and Technology No. 3, 2015, 45, 75-81
Category: Původní práce
Summary
Dose calculation algorithms implemented in the treatment planning software for Leksell Gamma Knife differ in their results, especially in the areas of steep electron density gradients. The Tissue Maximum Ratio (TMR) algorithm (in two variants) does not employ any patient-specific data besides the idealized skull shape, while the Convolution algorithm takes full advantage of voxel data from computed tomography (CT) to create a more faithful description of the anatomy.
The presented Monte Carlo model of Leksell Gamma Knife Perfexion was created in order to investigate dose distribution characteristics of the machine and to verify the mentioned algorithms. It builds upon Geant4 (a simulation toolkit for particle passage in matter) and being designed in a modular fashion, it enables to put several geometry components together at runtime. A precise description of the Perfexion collimation system is supplemented by voxel phantoms constructed from CT images in the DICOM format.
As a preliminary study, three specific plans of varying complexity were exported from the treatment planning software – a phantom for gel dosimetry and two clinical cases – and simulated using the Monte Carlo model. Scoring volumes were defined so that a direct dose distribution comparison could be made using three-dimensional gamma index analysis. All results show good agreement between the Monte Carlo method and calculated distributions with no significant difference between the algorithms (with over 99.9 % points satisfying the criteria ΔDM = 0,03 and Δdm = 1 mm). We plan to make further studies with more specific, artificially designed treatment plans in order to assess the subtle differences between the algorithms.Keywords:
gamma knife; Perfexion; voxel phantoms; Geant4; treatment planningIntroduction
Leksell Gamma Knife Perfexion (LGK, Elektra Instrument AB, Švédsko) is a stereotactic radiosurgery machine which is used for the treatment of many oncological, neurological and other diagnoses. It can irradiate precisely defined areas inside the patient’s head using collimated photon beams from 192 cobalt sources that together create a roughly ellipsoidal field (the major axis diameter being approximately 4, 8 or 16 mm, depending on the collimator setting). By combining multiple fields (called “isocentres” or “shots”), a complex dose distribution can be delivered while preserving the surrounding tissue and organs at risk.
The small stereotactic fields with sharp edges (especially that of the smallest “4-mm” collimator) pose a real challenge for both dosimetry (the fields are smaller than most available dosimeters and the situation is further complicated by the lateral charge particle non-equilibrium) and treatment planning (even a slight shift in position can result in a huge dose difference).
Leksell GammaPlan, a treatment planning system that comes with LGK, offers two dose calculation algorithms that differ in the extent to which they take into account information about patient’s anatomy:
Tissue Maximum Ratio (TMR) algorithm is characterized by a straightforward analytical approach. It is based on inverse square law and exponential attenuation. It does not work with anatomical details and treats the whole head as a uniform water phantom. The skull shape is approximated by cubic splines with measured radii (distances from surface to the centre of coordinate frame) at 24 different angles. There are two variants (TMR Classic and TMR 10) of this method with slightly different algorithms and different sets of configuration data [1].
Convolution algorithm was designed to enable precise dose estimation in areas with pronounced dose inhomogeneities. It builds on the collapsed cone convolution and pencil beam convolution methods. In contrast to TMR algorithms, patient’s anatomy – i.e. tissue material and skull shape from computed tomography (CT) data – is used in the calculation. On the downside, both computation and pre-treatment preparation (due to the necessity of CT scanning) are considerably more time-consuming [2].
We present a full Monte Carlo model of Leksell Gamma Knife Perfexion collimation system together with voxel phantoms constructed from real patient data. Its purpose is to enable comparison of the mentioned algorithms and evaluation of the clinical impact of the differences, potentially also to enable independent treatment plan verification. We include a preliminary study on three concrete treatment plans. It is expected that in the areas of varying tissue density, the Convolution algorithm should be superior to both TMR ones.
Methods
To obtain computer-simulated data, we used the Monte Carlo method for particle transport in matter. This method combines fundamental physics principles with random sampling to simulate results that would be impossible to calculate employing regular analytical methods. This is especially true for particle-matter interactions in complex geometries, such as voxel phantoms with a large 3D grid of voxels with different material properties.
In simulations, we used Geant4 toolkit [3] (version 9.6), a universal Monte Carlo framework for the passage of particles through matter that offers very high extensibility via user-provided C++ code. Individual parts of the model were combined using g4application, a plugin library and application for Geant4 (available from https://github.com/janpipek/g4application).
In this section, we describe in detail the construction and application of voxel phantoms (the employed software library, the process of input data preparation, and the scoring mechanism to provide a 3D dose map), the export of calculated dose maps from the treatment planning software, and the gamma index analysis which is used to compare the results.
Machine geometry and particle source
The geometrical model of LGK Perfexion was constructed using confidential information from the manufacturer, Elekta Instrument AB. It consists of a detailed model of the collimation system and a simplified description of the cobalt source – all volumes were defined in terms of conical and cylindrical elements and their Boolean combinations.
As input for the voxel phantom simulation, we used a set of particles stored in phase-space files after they traversed through the collimation system to the internal cavity of LGK. For each collimator size and ring (i.e. 15 combinations), this set of files contains the result of 1010 histories with initial angular biasing applied.
The machine model and the preparation of phase space files are described in more detail in article [4] where we obtained relative output factors and beam profiles of LGK Perfexion.
Voxel phantom library (g4application-dicom)
In Geant4, there is no built-in component for construction of voxel phantoms from patient CT data (usually stored in the DICOM format). We therefore took inspiration from one of the examples included in the Geant4 distribution and G4VoxelData library created by C.M.Poole [5], and developed g4application-dicom, a plugin for the g4application library that offers following features:
Import of DICOM data from a set of files. These are automatically sorted into a three-dimensional grid that can be cropped to the shape required by the study.
User-specified translation from Hounsfield units (HU) to materials understood by Geant4. In an external configuration file, consecutive ranges of HU are assigned element composition or Geant4-predefined materials with linearly interpolated densities over the range.
Construction of a volume containing voxels with properly assigned materials. This is implemented as three-level-deep hierarchy of volumes based on the G4PVReplica and G4PVParameterised classes. The volume can be translated and rotated via user commands.
Visualization. By user command, it is possible to turn on visualization where individual voxels receive colour based on the material. However, this is very demanding on CPU power in existing Geant4 visualization tools and therefore disabled by default.
g4application-dicom is distributed as open source and can be incorporated into other applications. It is available from https://github.com/janpipek/g4application-dicom.
Construction of voxel phantoms from input data
Employing the functionality of g4application-dicom, we constructed and used the voxel phantom in the following manner:
Data. The imaging data used in Leksell GammaPlan were exported (i.e. copied without change) from the system and read using g4application-dicom. No further manipulation with files was necessary as they were already in interpretable standard DICOM format.
Materials. The Convolution algorithm of LGP treats all tissue as water with varying electron density. A (linear) calibration curve is supplied by the user depending on the imaging machine used. We chose the same approach (and identical calibration curves) also in the Monte Carlo model. All material below −900 HU was treated as air, denser areas were considered to be water with a density function defined by the calibration curve of the used CT machine, Siemens SOMATOM Definition Flash.
Rotation and Translation. There are three coordinate systems in the model: DICOM coordinates are stored in the image files and describe the position of the patient at the time of imaging; frame coordinates correspond to the frame that is fixed to patient’s skull throughout the treatment process (all anatomical locations are expressed in this system); machine coordinate system is the “world” system used by Geant4 and it is fixed to the model of the machine itself.
The correspondence between DICOM and frame coordinates needs to be established manually by studying the image files. When patient is imaged, a special indicator box is attached to the stereotactic frame; this box contains fiducial markers, thin copper rods with known position in the frame coordinate system that leave circular spots in the images. With careful measurement, both translation and rotation between the systems can be established; a precision of ~0.5–1.0 mm can be reached for points in the studied volume. LGP provides a semi-automatic tool for establishing this correspondence; however, its results are not easily retrievable.
The relationship between frame and machine coordinates changes from shot to shot and is dependent on the isocentre position (which corresponds to the centre of machine coordinates) and the machine angle setting (70°, 90° or 110°).
In order to correctly place the voxel phantom with respect to the machine and particle source, rotation matrix and translation had to be calculated for each shot. This step can be done automatically and was a part of the application running script.
Scoring and dose calculation
To enable comparison with LGP dose matrices (that by default span points with user-specified grid size), we defined identical volumes and voxel sizes for scoring. It has to be noted that the scoring voxel grid is independent of the material voxel phantom defined in the geometry (the grid is placed directly into frame coordinates) – Geant4 realizes this using parallel geometries. Of the many approaches to scoring offered by Geant4, the most straightforward command-based scoring was used. We scored dose and total deposited energy.
After running simulations at the national computing grid MetaCentrum, we obtained 50 files for each shot , i.e. 10 estimations of the total dose produced by all sources in a particular collimation ring r. The contributions of the individual rings were summed according to their weight given by the number of source in the ring nr; the contribution of multiple shots were weighted based on their irradiation time ts:
Leksell GammaPlan dose matrices
Dose distribution can be exported from LGP in DICOM RT format – the file contains a 3-D array of 2-byte integer values of the relative dose and an absolute dose scaling parameter (as we were interested only in relative values, this parameter was not used).
Unfortunately, exported dose matrix is slightly shifted (by 0.1–0.8 mm) from the user-specified position (this was observed also in the case of calibration plan with standard phantom where symmetry in axial plane should be expected). We don’t know the cause yet; it remains a question for further analysis. However, we accounted for this shift by simple matching with simulated data (minimization of dose difference function) and using trilinear interpolation (finally, we cropped the matrices by one voxel from each side to a final dimension of to avoid NaN values).
Gamma index analysis
To numerically evaluate agreement between dose distributions D and D´, we used gamma index analysis. This method assigns to each point rl in a grid one number γ which minimizes the following function (defined for a pair of points i,j):
where ΔDM and ΔdM are two parameters of the analysis: dose to agreement parameter ΔDM specifies the maximum acceptable difference in relative dose and distance to agreement parameter ΔdM specifies the maximum acceptable displacement of the points.
Studied cases
We simulated dose distribution for three plans that were exported from the treatment planning system (both imaging data and dose calculated by each of the three algorithms). These plans included two real clinical cases and one experimental phantom: a neuralgia case with one 4-mm shot, a phantom for gel dosimetry based on Turnbull-blue dye with one 8-mm shot [6], and an adenoma case with 17 shots of different collimator sizes.
For each plan, we compared Monte Carlo data to distributions obtained from the three calculation algorithms of LGP: TMR Classic, TMR 10 and Convolution.
Tab. 1. The results of gamma analysis for various settings of Δd<sub>M</sub>. The percentage shows what fraction of points in the comparison of distributions from different algorithms and Monte Carlo method satisfy the condition γ ≤ 1 . Only points where relative dose exceeded 0.1 are taken into account. 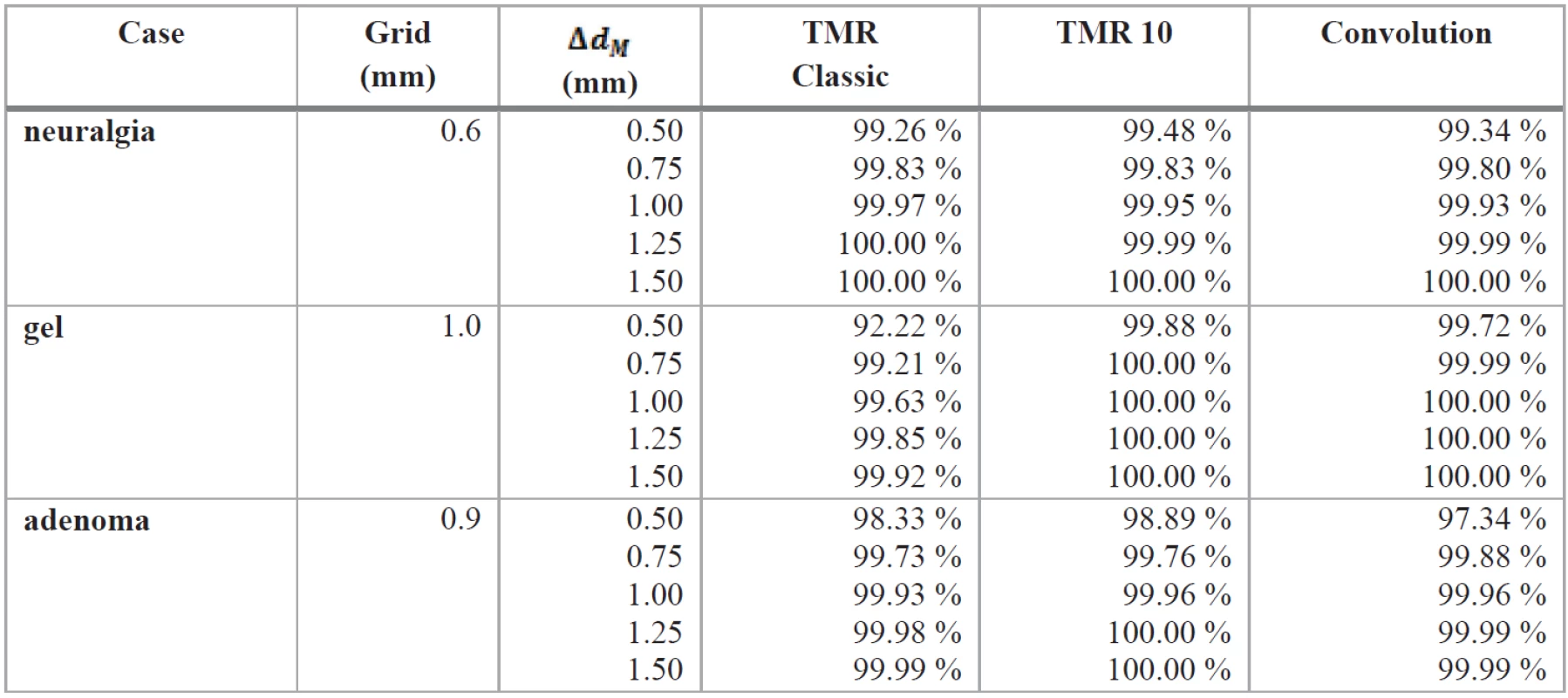
Results
A sample of visual comparison is included in Fig. 1, 3, and 5; relative dose contours are drawn on top of the HU values obtained from imaging data in a selected axial plane.
Fig. 1: Relative dose distributions of the neuralgia case in the axial plane Z = 91.3 mm. 
Fig. 3: Relative dose distributions of the gel phantom in the axial plane Z = 142.7 mm . 
Fig. 5: Relative dose distribution of the adenoma case in the axial plane Z = 103.0 mm. 
Gamma index analysis
In order to enable analysis with sufficiently low ΔdM values (the grid size was too large to enable setting small distance to agreement parameter), we trilinearly interpolated the distributions to a twice dense grid with a total of points. We performed a full gamma analysis on these sets using Python package called gamma_matrix (available from https://github.com/janpipek/gamma_index) for several values of the parameter ΔdM (0.5–1.5 mm) while keeping a fixed value of ΔDM = 0,03. We recorded the percentage of points that satisfy the condition γ ≤ 1.0; only points with the simulated relative dose over 0.1 were taken into account. The results are listed in Tab. 1. For each studied case, one example slice from the gamma index distribution in an axial plane is shown in Fig. 2, 4 and 6.
Fig. 2: The result of gamma index analysis of the neuralgia case for parameters Δd<sub>M</sub> = 1.0 mm and ΔD<sub>M</sub> = 0.03 , in the axial plane Z = 91.3 mm (same as in Fig. 1). The concentric rings of better and worse agreement are consistent with the differences observed in beam profiles of the 4-mm collimator studied in [4]. ![Fig. 2: The result of gamma index analysis of the neuralgia case for parameters Δd<sub>M</sub> = 1.0 mm and ΔD<sub>M</sub> = 0.03 , in the axial plane Z = 91.3 mm (same as in Fig. 1). The concentric rings of better and worse agreement are consistent with the differences observed in beam profiles of the 4-mm collimator studied in [4].](https://pl-master.mdcdn.cz/media/image/1e31fbbf8c8dfa5b3028a854fbd50ea6.jpg?version=1711874232)
Fig. 4: Gamma index of the gel phantom for parameters Δd<sub>M</sub> = 1.0 mm and ΔD<sub>M</sub> = 0.03 , in the axial plane Z = 142.7 mm (same as in Fig. 3). The concentric rings of better and worse agreement are consistent with the differences observed in beam profiles of the 8-mm collimator studied in [4]. ![Fig. 4: Gamma index of the gel phantom for parameters Δd<sub>M</sub> = 1.0 mm and ΔD<sub>M</sub> = 0.03 , in the axial plane Z = 142.7 mm (same as in Fig. 3). The concentric rings of better and worse agreement are consistent with the differences observed in beam profiles of the 8-mm collimator studied in [4].](https://pl-master.mdcdn.cz/media/image/64a0b8a71be5987b00b41c713cf956d2.jpg?version=1537794320)
Fig. 6: Gamma index of the adenoma case for parameters Δd<sub>M</sub> = 1.0 mm and ΔD<sub>M</sub> = 0.03 , in the axial plane Z = 103.0 mm (same as in Fig. 5). The area in the upper right corner of the Convolution image with high gamma corresponds to nasal cavity – this volume is considered to be outside the region of interest by the Convolution algorithm and no dose is calculated for it (although from the purely physics point of view, the dose in air has the same meaning as in tissue). This area is also not taken into account in the evaluation of passing points fraction. 
Discussion
In the gamma analysis results, there are certain discrepancies in the dose distributions when the lowest ΔdM is selected; however, with larger values the fraction of points satisfying the gamma index criterion quickly rises above 99.9 %. The difference between algorithms is not significant and the best fitting one changes from case to case.
Apparently, the selection of cases for the simulations was not optimal and the small variation in tissue density did not visibly influence the dose distribution (even close to tissue-air boundaries). For a more conclusive result, we plan to prepare artificial plans with more pronounced tissue inhomogeneities. However, in clinical experience, there is rarely a treatment plan in which the inhomogeneities play a more important role than in that of adenoma cases (one of the examined in this study).
Conclusion
We created a detailed Monte Carlo model of Leksell Gamma Knife Perfexion in Geant4 and prepared it for use with voxel phantoms constructed from DICOM imaging data.
Using this model, we compared three dose calculation algorithms available in the Leksell GammaPlan software to Monte Carlo simulations. We calculated and simulated dose distributions in three treatment plans of different complexity and performed gamma index analysis on the results. The agreement was very good (over 99.9 % points satisfying the condition for ΔDM = 0,03 and ΔdM = 1 mm) and there was no clear distinction between the algorithms.
From the patients’ perspective, this is a positive result as the dose calculated (and subsequently delivered) is not significantly dependent on the choice of calculation algorithm. However, the quantification of the impact remains an interesting topic for further research which will be based on more suitable treatment plans.
Acknowledgement
Access to computing and storage facilities owned by parties and projects contributing to the National Grid Infrastructure MetaCentrum, provided under the programme ‘Projects of Large Infrastructure for Research, Development, and Innovations (LM2010005)’, is greatly appreciated.
We would also like to thank Elekta Instrument AB for the geometrical description of the model including material data (provided under non-disclosure agreement) and especially to Håkan Nordström and Jonas Gårding for their help and consultation.
Mgr. Jan Pipek, Ph.D.
Faculty of Nuclear Sciences and Physical Engineering
Czech Technical University in Prague
Prague, Czech Republic
Zdroje
[1] Elekta Instrument AB A new TMR dose algorithm in Leksell Gammaplan®. Technical Report, 2011.
[2] Elekta Instrument AB The Convolution algorithm in Leksell Gammaplan® 10. Technical Report, 2010.
[3] Agostinelli, S. et al. Geant4–a simulation toolkit Nuclear Instruments and Methods in Physics Research A, 2003, vol. 506, p. 250–303.
[4] Pipek, J., Novotný, J., Novotný Jr., J., Kozubíková, P. A modular Geant4 model of Leksell Gamma Knife Perfexion. Physics in Medicine and Biology, 2014, vol. 59, p. 7609–7623.
[5] Poole, C.M. G4VoxelData, 2013–14,
https://github.com/christopherpoole/G4VoxelData
[6] Kozubíková, P., Šolc, J., Novotný Jr., J., Pilařová, K., Pipek, J., Končeková, J. Assessment of radiochromic gel dosimeter based on Turnbull Blue dye for relative output factor measurements of the Leksell Gamma Knife Perfexion. Journal of Physics: Conference Series, 2015, p. 573.
Štítky
Biomedicína
Článek vyšel v časopiseLékař a technika

2015 Číslo 3-
Všechny články tohoto čísla
- MONITORING VÝSKYTU PORÚCH OSOVÉHO ORGÁNU U ŠTUDENTOV DENTÁLNEJ HYGIENY
- COMPARISON OF DOSE CALCULATION ALGORITHMS FOR LEKSELL GAMMA KNIFE PERFEXION USING MONTE CARLO VOXEL PHANTOMS
- FEASIBILITY OF RADIOIODINE DOSIMETRY USING A SMALL FIELD OF VIEW GAMMACAMERA; PILOT STUDY
- DYNAMICAL CHARACTERISTICS OF SPEECH APPARATUS IN HUNTINGTON’S DISEASE
- RELIABILITA MERANÍ ZAŤAŽENIA NOHY PRI CHÔDZI
- Lékař a technika
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- RELIABILITA MERANÍ ZAŤAŽENIA NOHY PRI CHÔDZI
- MONITORING VÝSKYTU PORÚCH OSOVÉHO ORGÁNU U ŠTUDENTOV DENTÁLNEJ HYGIENY
- COMPARISON OF DOSE CALCULATION ALGORITHMS FOR LEKSELL GAMMA KNIFE PERFEXION USING MONTE CARLO VOXEL PHANTOMS
- FEASIBILITY OF RADIOIODINE DOSIMETRY USING A SMALL FIELD OF VIEW GAMMACAMERA; PILOT STUDY
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání





