-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaAnalýza dat v neurologii
XXXVIII. Možnosti grafického znázornění výstupů asociačních analýz kontingenčních tabulek
Autoři: L. Dušek; T. Pavlík; Jiří Jarkovský
; J. Koptíková
Působiště autorů: Institut biostatistiky a analýz MU, Brno
Vyšlo v časopise: Cesk Slov Neurol N 2013; 76/109(2): 251-256
Kategorie: Okénko statistika
Závěrem předchozího dílu seriálu jsme otevřeli otázku statistického srovnávání více nezávisle provedených odhadů poměru šancí (OR) nebo relativního rizika (RR). Tento problém je v klinickém a biomedicínském výzkumu velmi častý a týká se výstupů jak intervenčních randomizovaných studií, tak i observačních studií. Počet srovnávaných studií nerozhoduje, srovnávat lze samozřejmě výsledky již dvou nebo tří nezávislých experimentů, tak jako jsme to dokumentovali v příkladech XXXVII. dílu seriálu. Avšak s rostoucím počtem dílčích odhadů a studií klesá přehlednost a samozřejmě narůstá heterogenita a také pravděpodobnost zkreslení či chyby. Proto je při srovnávání více odhadů OR či RR velmi výhodné začít grafickým vykreslením dílčích odhadů. Pro tento účel se úspěšně ujala zvláštní forma grafického vyjádření, tzv. lesního grafu („forest plot“), který jsme krátce představili již v minulém díle seriálu.
Příklad takového grafu je uveden na obr. 1, který typicky zobrazuje odhady RR či OR (body) společně s jejich 95% intervaly spolehlivosti (horizontální úsečky) a s vyznačením referenční hodnoty 1. Připomeňme zde, že u poměrových indexů typu poměru šancí a relativního rizika znamená hodnota 1 bod nulového vlivu zkoumaného expozičního faktoru na sledovanou událost. Při takovém výsledku neumíme odlišit výskyt sledované události v exponované populaci (skupina případů, kohorta ovlivněná sledovaným faktorem) od jejího výskytu v kontrolní populaci. Pokud naopak interval spolehlivosti odhadu OR (RR) nepokrývá hodnotu 1, pak můžeme hovořit o statisticky významném vlivu sledovaného faktoru; při hodnotách OR (RR) > 1 jde o vliv rizikový, a naopak pokud je OR (RR) < 1, jde o faktor protektivní.
Obr. 1. Grafické srovnání více odhadů relativního rizika nebo poměru šancí pomocí tzv. lesního grafu (<i>„forest plotu“</i>). 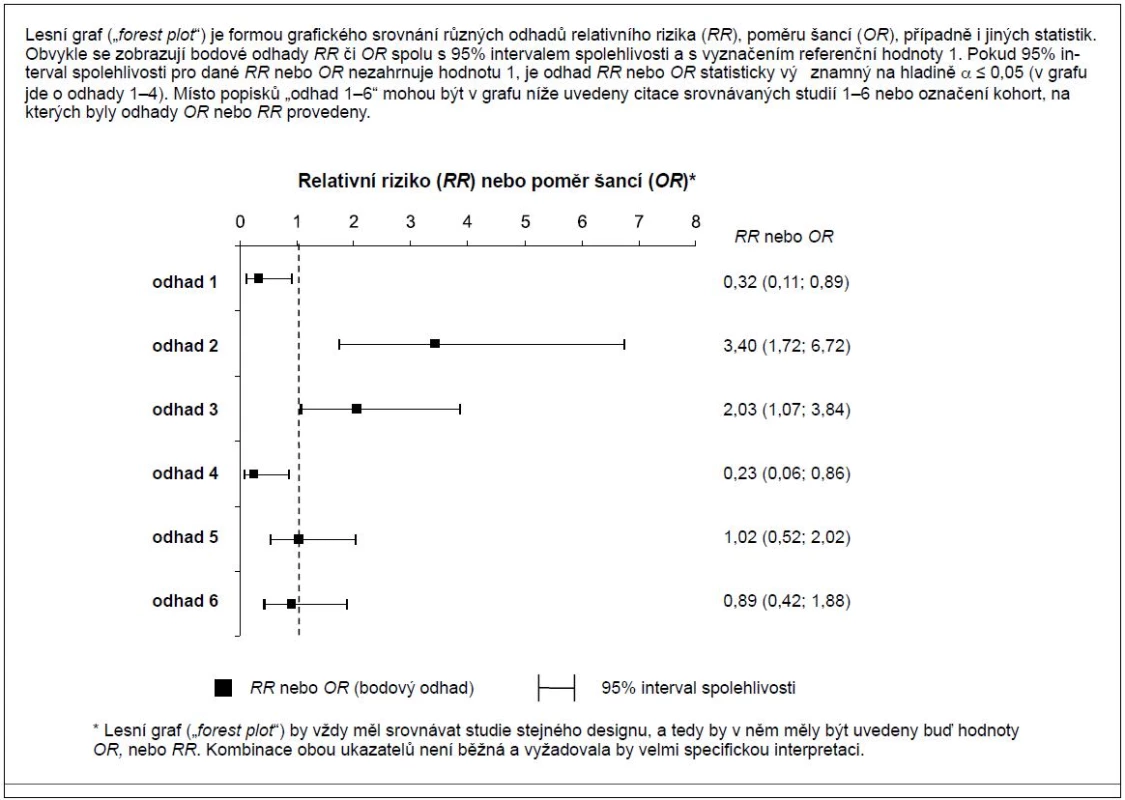
Lesní graf („forest plot“) představený na obr. 1 je typ zobrazení, které usiluje o přehledné znázornění více odhadů OR (RR) a jejich intervalů spolehlivosti. Věříme, že čtenáře přidaná hodnota těchto grafů zaujme. Velmi přehledně tak můžeme znázornit až desítky dílčích odhadů OR či RR, případně je i seřadit podle nějakého klíče, a čtenář jediným pohledem posoudí homogenitu či heterogenitu dílčích odhadů a porovnáním s referenční hodnotou 1 rovněž statistickou významnost jednotlivých odhadů. Lehce identifikujeme odlehlé studie (odhady), odhady vysoce statisticky významné a naopak odhady s hraniční významností. Uvedeme-li do grafu číselné hodnoty, nezůstane čtenář ochuzen ani o tabulkový přehled. Nelze se divit, že díky těmto možnostem lesní graf fakticky zdomácněl v prezentacích biomedicínského výzkumu. Ačkoli tato technika byla vyvinuta původně pro sumarizaci metaanalýz randomizovaných klinických studií (70.–80. léta minulého století), velmi rychle si našla své místo i v hodnocení studií observačních.
Lesní graf („forest plot“) lze v řadě atributů modifikovat a obohacovat o další informace, resp. dimenze relevantní pro srovnání dílčích studií. Horizontální číselnou osu můžeme vyjádřit přímo v hodnotách OR (RR) nebo můžeme použít logaritmované hodnoty odhadů. Logaritmovaná forma je někdy graficky přehlednější, zvláště pokud jsou dílčí odhady velmi heterogenní a mají široké intervaly spolehlivosti. Logaritmovaná forma nadto nabídne přehlednější zobrazení statisticky významných odhadů OR (RR) menších než 1, pro které v původní škále zůstává pouze úzký pás hodnot od 0 do 1. V díle XXXVI seriálu jsme rozebírali výpočty intervalů spolehlivosti pro OR (RR), které pracují s aproximací pomocí normálního rozdělení právě pro logaritmované hodnoty ln(OR) a ln(RR). Po odlogaritmování pomocí exponenciální funkce vždy získáváme asymetrické hranice intervalů spolehlivosti, jak ukazuje příklad na obr. 2. V logaritmované formě grafu je ovšem třeba dávat pozor na změnu referenční hodnoty odhadů pro nulový vliv, místo hodnoty 1 je to po logaritmické transformaci hodnota 0.
Obr. 2. Využití logaritmické transformace v grafickém srovnání více odhadů poměru šancí nebo relativního rizika. 
Současné počítačové programy nabízejí širokou škálu dalších možností, jak lesní graf („forest plot“) modifikovat. Body vyjadřující hodnoty odhadů OR (RR) lze kreslit s různou velikostí podle váhy, kterou dané studii (dílčímu odhadu) přikládáme (např. podle velikosti vzorku, reprezentativnosti studie apod.). Celkový vážený odhad OR (RR), nazývaný někdy také celkový výsledek nebo celkový vliv („overall effect“), může být graficky odlišen a vybaven graficky odlišeným intervalem spolehlivosti. Tyto modifikace a rozšíření grafického znázornění ukazují obr. 3 a 4. V obrázcích jsou rovněž uvedeny statistické testy využívané pro významnost celkového vlivu srovnávaných studií a pro hodnocení heterogenity dílčích studií. Tyto testy budeme detailně vysvětlovat v dalších dílech našeho seriálu, zde pouze konstatujme, že jejich výsledek lze odečíst přímo z lesního grafu:
Obr. 3. Ukázka informačních možností lesního grafu (<i>„forest plot“</i>) . 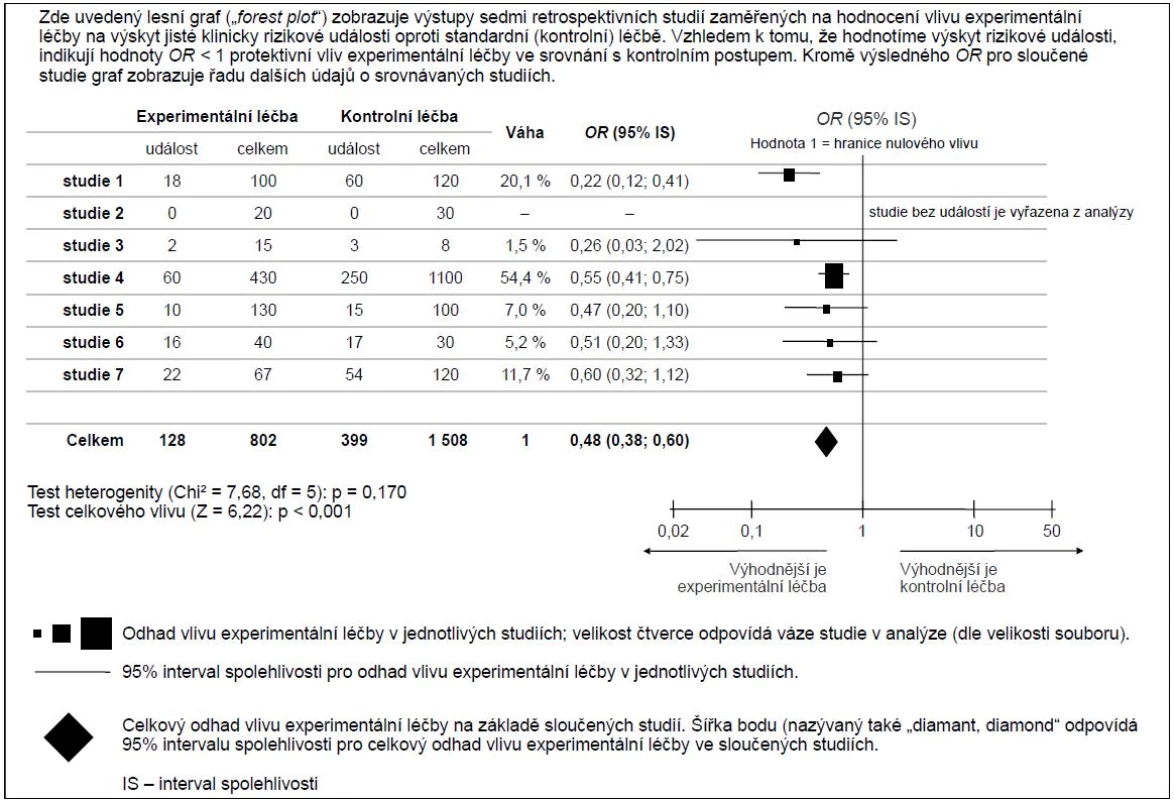
Obr. 4. Lesní graf (<i>forest plot</i>) pro srovnání studií s různým cílovým parametrem (poměr šancí a rozdíl průměrů). 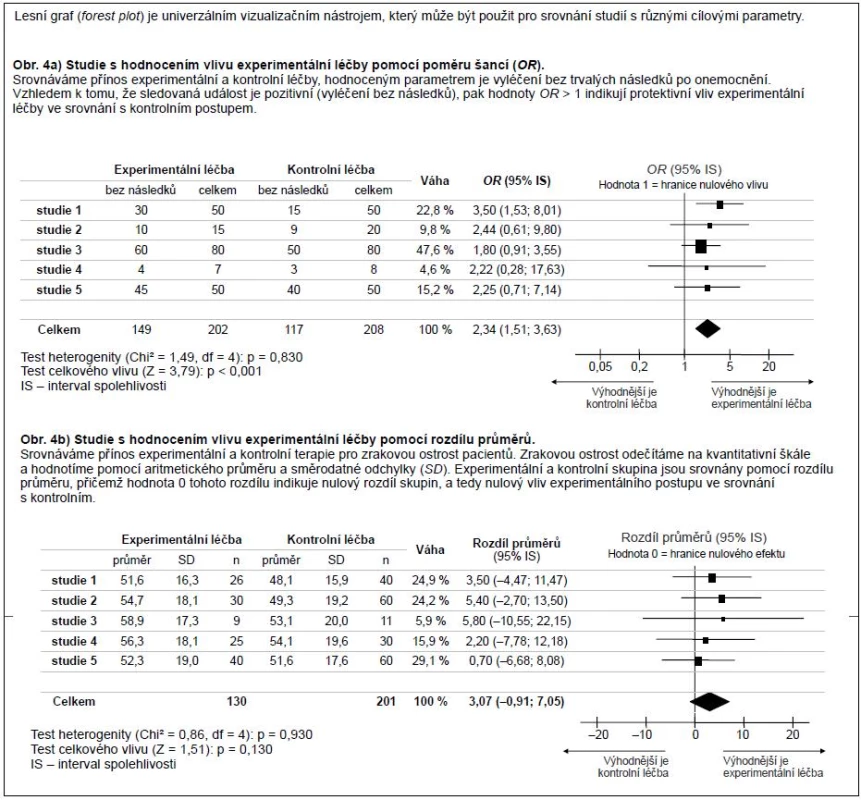
- statisticky významný celkový efekt je větší nebo menší než referenční hodnota 1 a jeho interval spolehlivosti tuto hodnotu nezahrnuje,
- homogenní, tedy vzájemně konzistentní, výstupy dílčích studií jsou patrné z pozic dílčích odhadů OR nebo RR; velmi snadno rovněž vidíme i odlehlou studii, která např. dává opačné výsledky než ostatní apod.
Lesní graf („forest plot“) lze samozřejmě využít i pro odhady jiných statistik než OR (RR), princip zůstává stejný. Vždy srovnáváme více dílčích a stejně zaměřených studií a vykreslujeme odhady použité statistiky s jejich intervaly spolehlivosti. Obr. 4b přináší příklad grafu, který místo OR (RR) pracuje s odhady aritmetického průměru a jejich směrodatnými odchylkami. V takovém případě již ovšem nejde o asociační studii, v obou srovnávaných ramenech byla měřena kvantitativní náhodná veličina (např. koncentrace látky v krvi pacientů a kontrol). Náhodnou veličinu statisticky popisujeme aritmetickým průměrem a rozdíl odhadů průměru mezi experimentální a kontrolní skupinou osob, společně s jeho intervalem spolehlivosti, jsou vstupem do lesního grafu (obr. 4b).
Je patrné, že do lesního grafu může vstupovat poměrně široké spektrum statistik, které využíváme pro srovnání ramen klinických studií. Jelikož se v takových experimentech většinou zabýváme vlivem nějakého faktoru (diagnostika, léčba, rizikové faktory, protektivní faktory) na událost na výstupu (vyléčení pacienta, úmrtí pacienta, relaps nemoci apod.), hovoříme o tzv. ukazatelích vlivu („outcome measures“ nebo „effect measures“). V zásadě můžeme dvě srovnávané kohorty (např. pacienty a kontroly) odlišit poměrem nebo rozdílem hodnot náhodné sledované veličiny („outcome“). U poměru dvou číselných charakteristik je referenční hodnotou pro nulový rozdíl mezi skupinami hodnota 1, u absolutního rozdílu číselných charakteristik je to potom hodnota 0.
Závěrem této grafické části seriálu se opět vraťme k asociačním studiím a jejich základnímu výstupu v podobě tabulek četností. Pro vyjádření významnosti a vzájemné závislosti řádků a sloupců v těchto tabulkách se využívají i další typy grafů, které mohou zvláště u objemnějších dat významně usnadnit jejich prezentaci. Zejména autoři genetických asociačních studií, kteří typicky pracují s velkým počtem genetických markerů, často sahají k různým grafickým pomůckám. Ačkoli nejde o grafy zcela běžné, stojí za to se o nich zmínit, neboť jejich realizace není při dostupnosti počítačové techniky nijak problematická. Formou příkladů tak uvádíme tzv. graf asociací („association plot“; obr. 5) a tzv. mozaikový graf („sieve plot“; obr. 6), které se zaměřují na zobrazení rozdílů mezi pozorovanými a očekávanými četnostmi v tabulce četností. Očekávané četnosti reprezentují stav, který by teoreticky nastal v případě nulového vztahu mezi srovnávanými jevy. Přehled užitečných grafů uzavírá tzv. růžicový graf („rose plot“; obr. 7), který je variantou běžného koláčového grafu. Přidanou hodnotu těchto zobrazení samozřejmě oceníme především u složitých kontingenčních tabulek s více řádky a sloupci.
Obr. 5. Graf asociací (<i>„association plot“</i>) jako nástroj vizualizace kontingenčních tabulek. 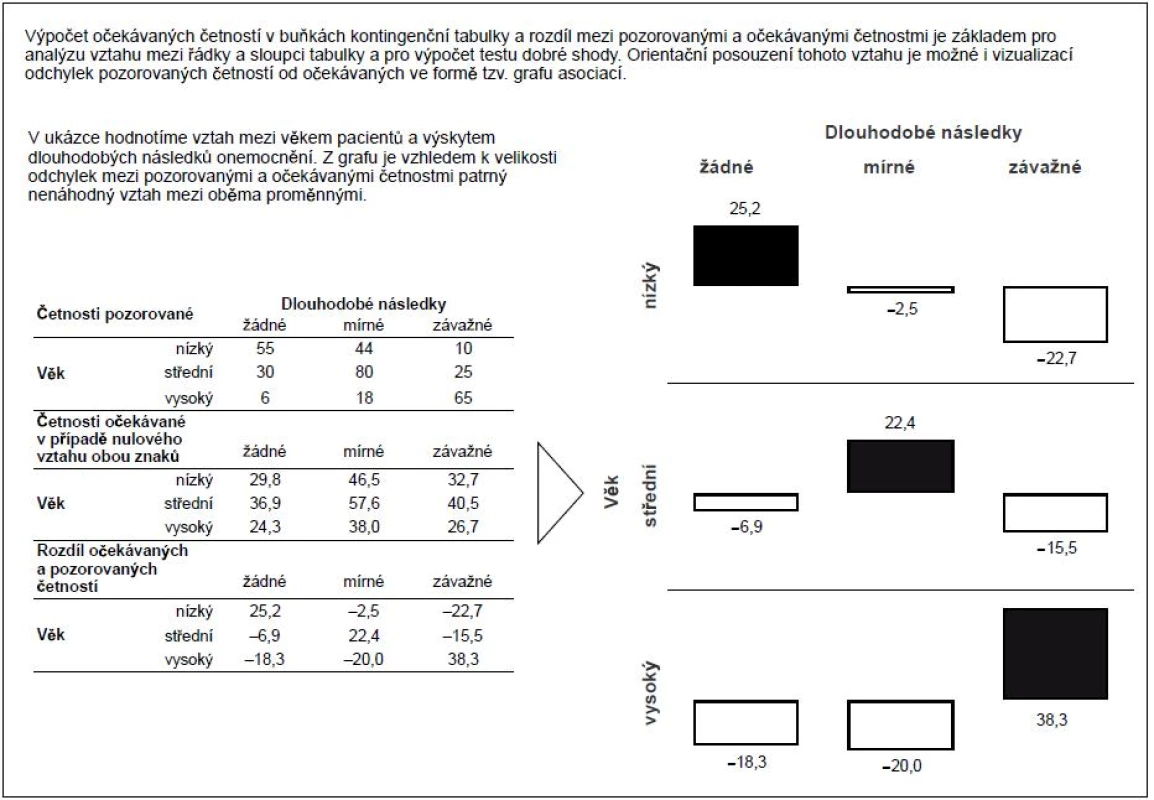
Obr. 6. Mozaikový graf (<i>„sieve plot“</i>) jako nástroj vizualizace kontingenčních tabulek. 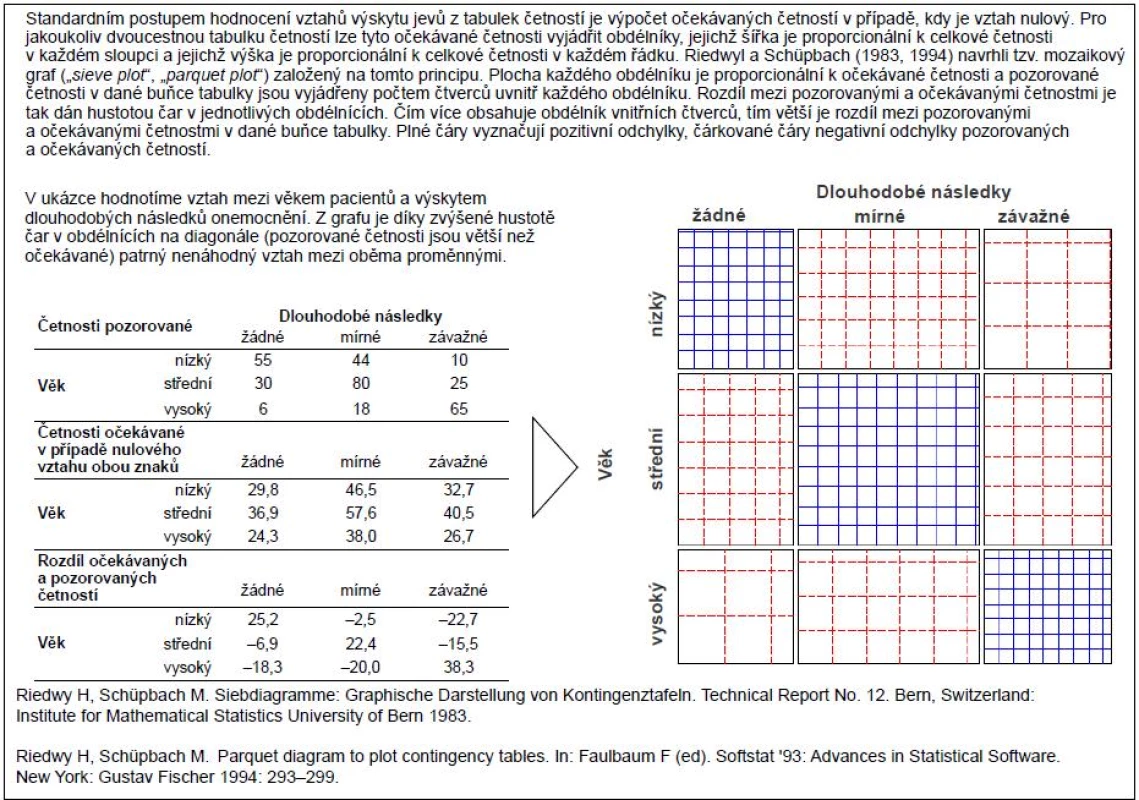
Obr. 7. Růžicový graf (<i>„rose plot“</i>) jako nástroj vizualizace kontingenčních tabulek. 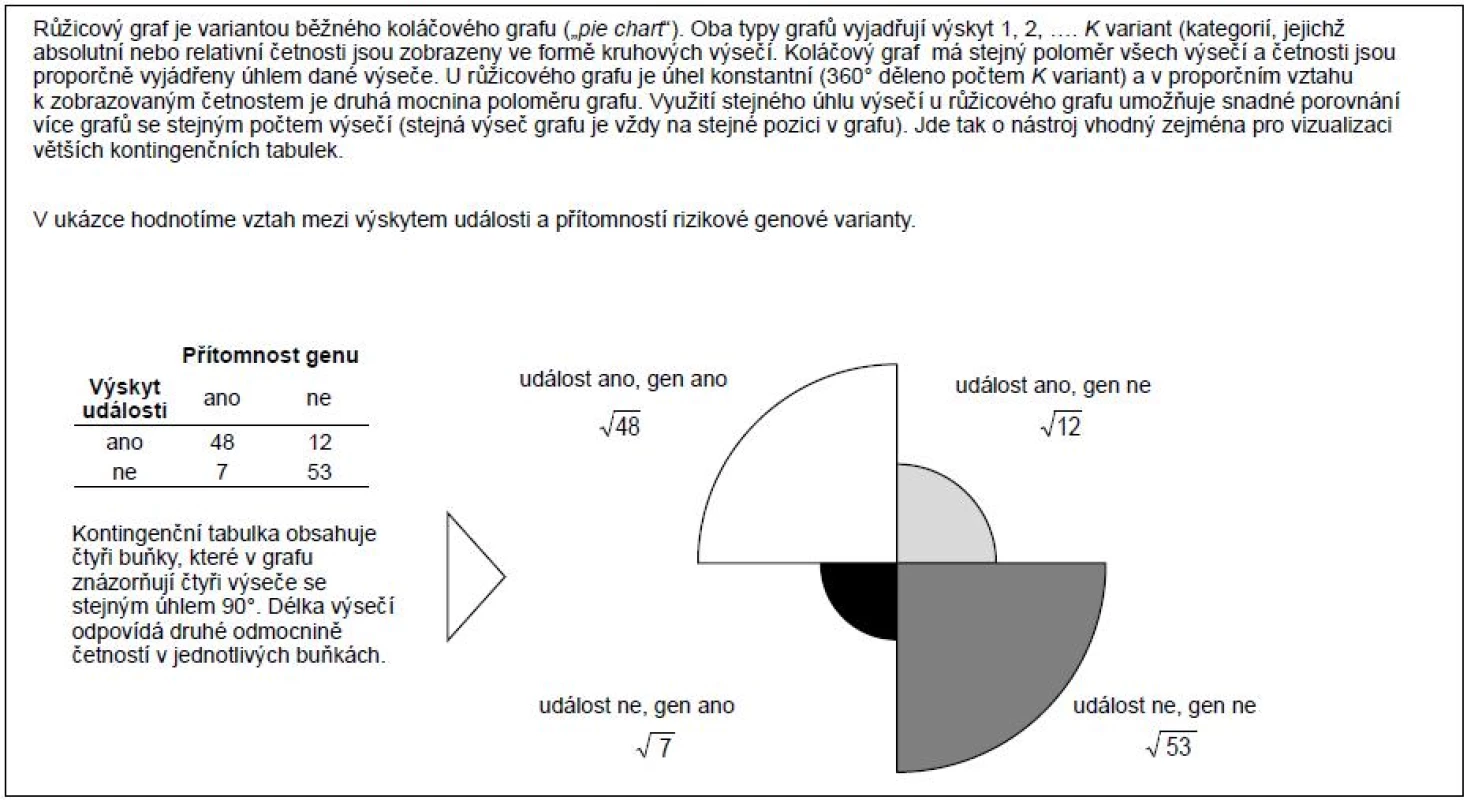
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
MU, Brno
e-mail: dusek@cba.muni.cz
Štítky
Dětská neurologie Neurochirurgie Neurologie
Článek Nové pokyny pro autoryČlánek Habituace je významnější na pohybový podnět ve srovnání s reverzačním podnětem – pilotní studieČlánek Pozdní forma Tay-Sachsovy choroby napodobuje spinální svalovou atrofii III. typu – dvě kazuistikyČlánek Endoskopická ventrikulocisternostomie u dětí s předchozí implantací ventrikuloperitoneální drenážeČlánek Webové okénko
Článek vyšel v časopiseČeská a slovenská neurologie a neurochirurgie
Nejčtenější tento týden
2013 Číslo 2- Rozpoznejte periferní neuropatii – dotazník pro pacienty, podpora pro lékaře
- Vitamin B12 − mnoho různých forem, žádný rozdíl v absorpci
- Tři jsou více než jeden: Kombinace 3 vitaminů skupiny B prodlužuje délku neuritů
- Metamizol jako analgetikum první volby: kdy, pro koho, jak a proč?
- Magnosolv a jeho využití v neurologii
-
Všechny články tohoto čísla
- Nové pokyny pro autory
- Creutzfeldtova-Jakobova choroba
- Elektrofyziologické vyšetření pánevního dna
- Význam a limitace zrakových evokovaných potenciálů ve studiu patofyziologie migrény
- Habituace je významnější na pohybový podnět ve srovnání s reverzačním podnětem – pilotní studie
- Rozdíly v modulaci kortikální aktivity u pacientů po cévní mozkové příhodě s reziduální spasticitou ruky léčených botulotoxinem A
- Vyhodnocení sběru epidemiologických dat u cévních mozkových příhod z registru IKTA. Incidence cévních mozkových příhod v okrese Zlín
- Komentář k práci Z. Kality et al. Vyhodnocení sběru epidemiologických dat u cévních mozkových příhod z registru IKTA. Incidence cévních mozkových příhod v okrese Zlín
- Úloha neurootologa v záchytu poradiačních komplikací u pacientů s vestibulárním schwannomem léčených Leksellovým gama nožem
- X-viazaná adrenoleukodystrofia
- Sonograficky navigované operace mozkových kavernomů
- Endoskopická ventrikulocisternostomie u dětí s předchozí implantací ventrikuloperitoneální drenáže
- Diagnostika, terapie a dispenzarizace meningeomů na NCHK FN Brno v letech 2005–2010
- Normotenzní hydrocefalus – komplikace z předrénování a jejich závislost na použitém ventilu
- Pozdní forma Tay-Sachsovy choroby napodobuje spinální svalovou atrofii III. typu – dvě kazuistiky
- Spinocerebelární ataxie typ 7 (SCA7) – kazuistika
- Lymeská borelióza jako příčina bilaterální neuroretinitidy s výraznou jednostrannou hvězdicovitou makulopatií u osmileté dívky
- Zriedkavejšia príčina obštrukčného syndrómu spánkového apnoe – morbus Madelung. Kazuistiky
- X-vázaná myotubulární myopatie u dvou bratrů v důsledku nové mutace v MTM1 genu – kazuistiky
- Tortikolis při Griselově syndromu – kazuistiky
- Webové okénko
-
Analýza dat v neurologii
XXXVIII. Možnosti grafického znázornění výstupů asociačních analýz kontingenčních tabulek
- Česká a slovenská neurologie a neurochirurgie
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Creutzfeldtova-Jakobova choroba
- Spinocerebelární ataxie typ 7 (SCA7) – kazuistika
- Lymeská borelióza jako příčina bilaterální neuroretinitidy s výraznou jednostrannou hvězdicovitou makulopatií u osmileté dívky
- Elektrofyziologické vyšetření pánevního dna
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Revma Focus: Spondyloartritidy
nový kurz
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání



