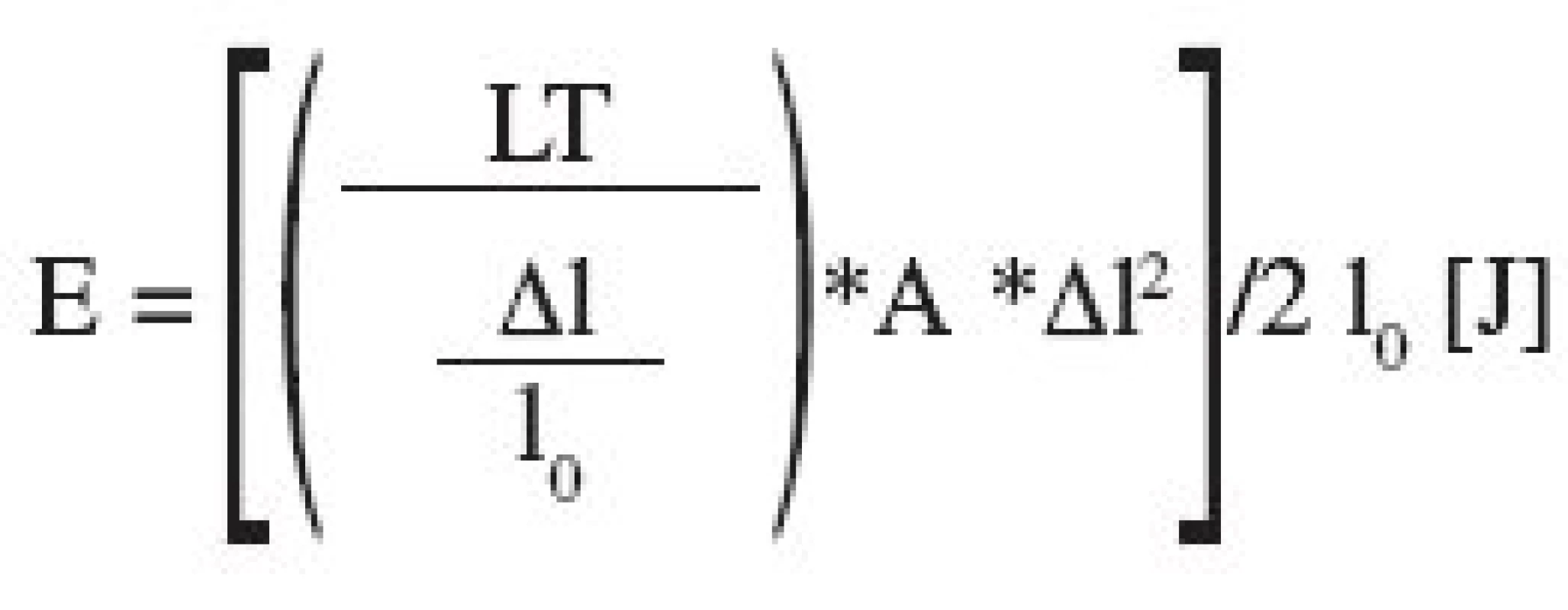-
Medical journals
- Career
- Contact
Characterization of celluloses by means of viscoelastic parameters
Authors: M. Řehula; R. Adámek
Authors‘ workplace: Charles University in Prague, Faculty of Pharmacy in Hradec Králové, Department of Pharmaceutical Technology
Published in: Čes. slov. Farm., 2008; 57, 215-220
Category: Original Articles
Overview
In tablet formulation it is necessary to start from viscoelastic parameters of the excipients employed. Plasticity and elasticity of excipients are influenced by the type of bonds which are being formed in the course of the compaction process. The present paper evaluates the viscoelastic properties of selected fillers intended for direct compaction of tablets. The determinations included cellulose powder, microcrystalline celluloses Avicel PH 101, Avicel PH 102, Avicel PH 103, Avicel PH 200, Avicel PH 301, and Ceolus KG 802. Elasticity of the excipients was evaluated by means of Young’s modulus of elasticity and differential elastic potential energy. Plasticity was evaluated by means of the stress relaxation test using the three-exponential equation following Maxwell’s model. The method was supplemented with a novel original parameter, total plasticity PT. The study examined the effect of particle size of fillers, density, moisture content, and molecular weight on elasticity and plasticity of celluloses. The results of the paper revealed that particle size of celluloses did not influence elasticity and plasticity of excipients. With increasing density of celluloses, elasticity was increased and at the same time plasticity was decreased. The above-mentioned viscoelastic parameters were influenced by the content of moisture in fillers. With increasing amount of moisture in fillers, elasticity was decreased and plasticity increased. With increasing molecular weight of cellulose, elasticity was decreased and plasticity increased.
Key words:
Young’s modulus of elasticity – differential elastic potential energy – three-exponential equation of plasticity – residual and total plasticity – cellulosesIntroduction
Elasticity and plasticity are usually considered to be the principal viscoelastic properties. Elastic deformation can be defined as a reversible change in the shape or volume of material resulting from force, when after the action of force is completed, material returns to its original shape 1).Elastic deformation is time-independent and fully restorable.
Plastic deformation can be defined as a permanent change in the shape of material resulting from applied tension 1). The same author further points out that viscoelasticity reflect the time-dependent character of deformation.
In the evaluation of viscoelastic properties of fillers, four groups of methods are employed; the method based on the “force-route” record 2, 3), elastic recovery 4), creep test 5), and stress relaxation 6).
The present study evaluated plasticity of fillers by means of the stress relaxation test. If during compaction after reaching the maximal compaction force the upper punch is stopped and the volume of the tablet is left constant for a certain period of time, we can observe an exponential decrease in the strength in the tablet. Stress relaxation can thus be defined as a decrease in compaction force in time while keeping a constant volume of the material under compaction 7). The extent of relaxation depends on the amount of energy stored in the tablet during compaction and also on bond formation 8).
For the evaluation of the decrease in strength during the test, one - to four-exponential equations are used 9). The authors studied the behaviour of relaxation to 360 s and found that the graph of the decrease in strength in dependence on time corresponded to Maxwell’s body 30 s after achieving the maximal strength. This model is composed of a spring and piston arranged in a series. The spring represents the elastic properties and the piston the plastic ones. The following equation corresponds to such a model:
F(t) = FMAX exp(t/T)
where F(t) is strength in time t and FMAX themaximal strength in time 0, T is the time constant.
Other authors 10) in their book present a simplified variant of the equation (E1–3 – modulus of elasticity):
F(t) = E1-t/T1 + E2-t/T2 + E3-t/T3
This study used the stress relaxation method to evaluate the viscoelastic characteristics of the fillers cellulose powder, and microcrystalline celluloses Avicel PH 101, Avicel PH 102, Avicel PH 103, Avicel PH 200, Avicel PH 301, and Ceolus 802.
Experimental part
Raw materials used
The model pharmaceutical fillers for direct compression were the microcrystalline celluloses Avicel PH 101 (lot 6902C), Avicel PH 103 (lot Z726C), Avicel 301 (lot P926C), all manufactured by the firm FMC Corporation, Belgium; cellulose powder Vitacel A 300 (lot 0708050429), J. Rettenmaier, Germany, Ceolus KG-802 (lot K3B1), Asahi Kasei Chemicals Corporation, Japan. All materials comply with the European Pharmacopoeia and were used without any adjustments.
Preparation of tablets
Tablets of a diameter of 13 mm and weight of 500 mg were compacted in a compaction preparation (Adamus HT, Machine Factory Group, Szczecin, Poland) in a device for testing the strength of materials under tension and pressure T1-FRO 50 (Zwick GmbH, Ulm, Germany). Adjustment of the device: distance of jaws, 117 mm, rate of the cycle, 2 mm/s, pre-load, 2 N, compaction forces, 250 N, 500 N, 1000 N, 2000 N, 3000 N, 4000 N, 5000 N, 7500 N, 10000 N, 12500 N, and 15000 N. For the determination of Young’s modulus of elasticity and elastic potential energy, tablets were compacted without a pause; for the determination of stress relaxation, tablets were compacted with a pause of 180 s. During the pause, the upper punch was stopped at the point where it reached the maximal strength, and the decrease in strength in the punch in dependence on time was recorded. In each compaction force, six tablets were evaluated.
When compaction was finished, the height of each tablet was measured (a digital micrometric screw Mitotuyo, Japan).
Calculation of Young’s modulus of elasticity
Young‘s modulus of elasticity was calculated according to the equation:
CP = EY *Δl/l ,
where CP is compaction pressure, EY Young’s modulus of elasticity, and Δl/ldeformation expressed as the ratio of the change in the length of the body to the original height. The term Δl is the difference of heights of the tablets 5 s after completion of compaction and the height at the maximal pressure, l is the height of the tablet at the maximal pressure. In the graphic representation of the dependence of CP on l/l, the gradient of the developed line is the Young’s modulus of elasticity which is searched for.
Calculation of elastic potential energy
The following equation served to calculate elastic potential energy, which causes the increase in height of the tablet after the completion of compaction 11):
where A is the area of the tablet (m2), other terms are explained above.
The differences in elastic potential energy of the tablets compacted without a pause and those with a pause yielded differential elastic potential energy (J).
Calculation of stress relaxation parameters
To calculate the parameters of the decrease in strength in the tablet at 180 s with a pause, the following three-exponential equation is employed:
CP = E1e-t/T1 + E2e-t/T2 + E3e-t/T3 [MPa]
Parameters of the above-mentioned equation were calculated using the programme OriginPro 7.5 by means of the function ExpDec3. The parameter CP (MPa) is the compaction pressure at a given moment in time t (s), E1 3 (N) is the amount of strength which was decreased in the given process, T1-3 is the relaxation constant which states the rate and the steep gradient of the process. The residual plasticity PR (MPas) is calculated from the following equation 10):
PRi = Ei * Ti [MPas]
for each compaction pressure. The total plasticity PT (MPas) is then equal to the area under the curve of the graph of the dependence of PR/CP on CP.
Results and discussion
The stress relaxation test was employed to evaluate plasticity. The results obtained in this test expressing the decrease in compaction pressure in dependence on time were evaluated by means of a three-exponential equation. This equation corresponds to three Maxwell’s models arranged in parallel10). The springs E1–3 represent the elastic modulus, the pistons PR1–3, the plastic modulus. After compaction of the material by a certain pressure, a certain value of the spring E and the zero value of PR are achieved.
The given relation divides the whole process of decrease in compaction pressure in dependence on time into three processes. According to the present authors’ idea, in the first process a high decrease in the modulus E1 is due to the extension of the spring in order to achieve greater mutual approximation of the surfaces of the particles. The given approximation does not result in the development of new bonds yet. That is why the increase in the value of the modulus of the residual plasticity PR1 is minimal. In the second process it can be assumed that by the action of smaller released elastic energy further approximation of the surfaces of the particles occurs and conditions are produced for the development of bonds. In the third process, the elastic modulus E3 possesses approximately the same value as the parameter E2 and at the same time a high value of the modulus of the residual plasticity PR3. This process is called the plastic process, in which deformation is not restorable and the process is time-dependent 12–14). In the third process, only a small amount of elastic energy suffices for further approximation of the surfaces of the particles and development of bonds.
Viscoelastic properties were studied in cellulose powder and in microcrystalline celluloses, which possess substantially smaller molecular weights than cellulose powder. The microcrystalline celluloses employed differ in the sizes of particles, densities, and moisture content.
The obtained results are shown in Tables 1 and 2 and in Figures 1–6. In the graphs there are obviously great standard deviations in some parameters. They are caused by close affinities of the excipients tested and further by the use of original methodologies producing greater variability of results.
1. Values of elastic parameters of celluloses. EY Young’s modulus of elasticity and EEP differential elastic potential energy (X arithmetic mean, s standard deviation) 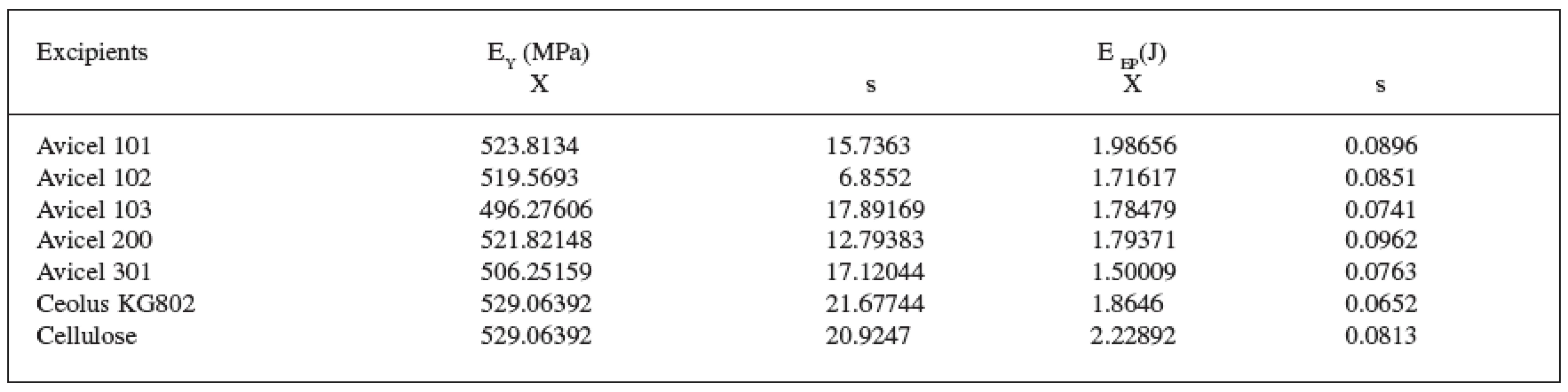
2. Value of total plasticity PT of celluloses (X arithmetic mean, s standard deviation) 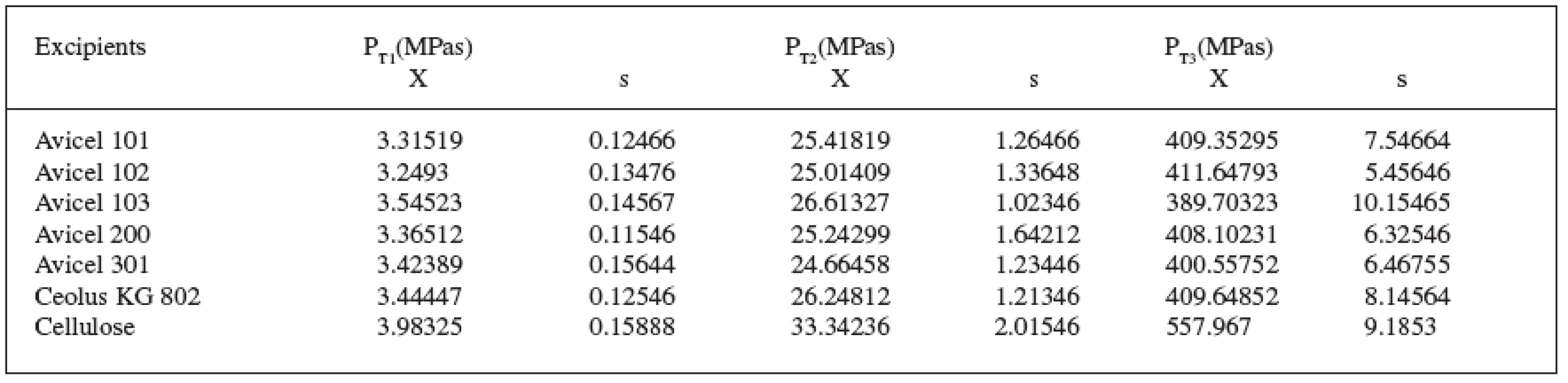
1. Relationship between compaction pressure and Δl/l0 
2. Effect of factors under study on Young’s modulus of elasticity in celluloses 
3. Effect of factors under study on E differential elastic potential energy in celluloses 
4. Effect of factors under study on total plasticity PT1 in celluloses 
5. Effect of factors under study on total plasticity PT2 in celluloses 
6. Effect of factors under study on total plasticity PT3 in celluloses 
The first marker under evaluation was molecular weight of the celluloses. Cellulose powder possesses the molecular weight of about 243000, microcrystalline celluloses only about 36000 15). For the evaluation of viscoelastic parameters, a comparison was made of the properties of cellulose powder and the microcrystalline cellulose Avicel PH 102. Young’s modulus of elasticity in cellulose powder in comparison with Avicel PH102 was higher by 10 MPa and differential elastic potential energy was higher by 0.51 J. The higher values in both cases mean lower elasticity. On the other hand, the values of plasticity in all three processes were higher in cellulose powder. The parameter PT1 was higher by 0.73 MPas, the parameter PT2 higher by 8.33 MPas, and the parameter PT3 higher by 146.32 MPas. Cellulose powder in contrast to Avicel PH 102 thus showed lower elastic properties and at the same time higher plasticity. These regularities are caused by the type and number of bonds which are being formed during compaction process. Cellulose powder, in contrast to Avicel PH 102, possesses a low crystalline share and at the same time a larger amorphous share, which on compaction readily forms hydrogen bonds. Also in cellulose powder, in contrast to Avicel PH 102, the principle of mechanical interlocking plays its role 16).
Another marker under evaluation is particle size. In this part of the study, Avicel PH 101 with a particle size of 50 μm, Avicel PH 102 with a particle size of 100 μm, and Avicel PH 200 with a particle size of 180 μm were compared. The values of Young’s modulus of elasticity ranged from 522 to 524 MPa, the values of differential elastic potential energy from 1.72 to 1.99 J, and the values of plasticity PT1 from 3.25 to 3.36 MPas, PT2 from 25.01 to 25.41 MPas, and PT3 from 408.10 to 411.65 MPas. The results cannot clearly demonstrate the effect of particle size on viscoelastic properties of microcrystalline celluloses. It is due to the method of production, when the primary needle-shaped objects of the size of about 20 μm granulate into the objects of varying particle sizes. The microcrystalline celluloses under study of varying sizes therefore possess the same compaction properties.
Another important factor is the density of microcrystalline celluloses. The comparison included Ceolus KG 802 with a density of 0.2 g/cm2, Avicel PH 101 with a density of 0.3 g/cm2, and Avicel PH 301 with a density of 0.4 g/cm215). Young’s modulus decreased with increasing density from 529 to 506 MPa and differential elastic potential energy decreased from 1.99 to 1.50 J. With a decrease in the values of the above-mentioned parameters, elasticity of microcrystalline celluloses was increased. The parameter of plasticity PT1 ranged from 0.44 to 3.32 MPas. With low values it is not possible to assume a significant influence of the factor under studies. The parameter PT2 decreased from the value of 26.25 MPas to the value of 24.66 MPas and the parameter PT3 also decreased from the value of 406.65 MPas to the value of 400.56 MPas. Plasticity of microcrystalline celluloses generally decreased with increasing density.
The final parameter under evaluation was the declared moisture content of microcrystalline celluloses, comparing Avicel PH101 with a moisture content of 5% and Avicel PH 103 with a moisture content of 3%.
Young’s modulus of elasticity in Avicel PH 101 was 524 MPa and in Avicel PH 103 496 MPa. Differential elastic potential energy in Avicel PH 101 was 1.99 J and in Avicel PH 103, 1.79 J. With a decreasing moisture content in the particles of microcrystalline cellulose, elasticity was increased. When comparing plasticities, with an increasing moisture content the parameter PT1 ranged insignificantly from 3.32 MPas to 3.55 MPas, the parameter PT2 ranged insignificantly from 25.41 MPas to 26.25 MPas. On the other hand, the principal parameter necessary for the formation of bonds PT3 decreased with decreasing moisture from 409.35 MPas to 389.70 MPas. A decreasing moisture content in microcrystalline celluloses decreases plasticity by decreasing the number of hydrogen bonds, which are being formed during compaction process.
An important characteristic of fillers is their plasticity. The present paper has demonstrated that cellulose powder possesses higher plasticity than other microcrystalline celluloses. Furthermore, it has been demonstrated that plasticity is not influenced by particle size of microcrystalline celluloses. Plasticity is further increased with decreasing density of microcrystalline celluloses and increasing moisture in the particles of microcrystalline celluloses.
The paper was supported by the Research Project MSM 0021620822.
Received 11 August 2008 / Accepted 20 August 2008
Address for correspondence:
Assoc. prof. RNDr. Milan Řehula, CSc.
Univerzita Karlova v Praze, Farmaceutická fakulta v Hradci Králové, Katedra farmaceutické technologie
Heyrovského 1203, 500 05 Hradec Králové
e-mail: milan.rehula@faf.cuni.cz
Sources
1. Brittain, H. G.: Physical characterization of pharmaceutical solids. New York, Marcel Dekker Inc., 1995; 288.
2. Stamm A., Mathis, C.: Acta Pharm. Technol. Suppl. 1, 1976a; 7–16.
3. Podczeck, F., Wenzel, U.: Pharm. Ind., 1989; 51, 524–527.
4. Krycer, I., Pope, D.G., Hersey, J.A.: Drug Develop. Ind. Pharm., 1982; 8, 307–342.
5. Tsardaka, K.D., Rees, J.E.: J. Pharm. Pharmacol. 1989; 41, 28P.
6. Cole, E.T., Rees, J, E., Hersey J.A.: Pharm. Acta Helv., 1975; 50, 28–32.
7. Lieberman, H. A., Rieger, M. M., Banker, G. S.: Pharmaceutical Dosage Forms: Disperse systems. Vol. 1., second edition. Marcel Dekker Inc. New York, 1996; 168.
8. Maarschalk, K. V., Zuurman, K., Vromans, H. et al.: Int. J. Pharm., 1997; 151, 27–34.
9. Rees, J. E., Rue, P. J.: J. Pharm. Pharmacol., 1978; 30, 601–607.
10. Manas, Ch., Salil, K. R.: Plastics Technology Handbook. New York, CRC Press, 2007; 260.
11. Wikipedia Encyclopedia: Young’s modulus. http://en.wikipedia.org/wiki/Young‘s_modulus 9.4.2008
12. Bonacucina, G., Di Martino, P., Piombetti, M. et al.: Int. J. Pharm., 2006; 313, 72–77.
13. Lum, S. K., Duncan-Hewitt, W. C.: J. Pharm. Sci., 1998; 88, 261–276.
14. Markwood, W. H., Spurlin, H. M.: Residual stresses and strains in molded plastics. Presented at the Annual Meeting of the Society of Rheology, Chicago, Illinois, 1951.
15. Rowe, R. C., Sheskey, P. J., Owen, S. C.: Handbook of Pharmaceutical Excipients, Fifth Edition. Londýn, Pharmaceutical Press, 2006; 330–343.
16. Aldeborn, G., Nyström, Ch.: Pharmaceutical powder compaction technology. Marcel Dekker Inc., New York, 1996; 7–8, 428–479.
Labels
Pharmacy Clinical pharmacology
Article was published inCzech and Slovak Pharmacy

2008 Issue 5-
All articles in this issue
- History and the present state of hypolipidaemic therapy
- Effect of montelukast on the treatment of asthma bronchiale in pediatric patients with perennial allergic rhinitis
- Impact of demographic factors on consumption of pharmaceuticals in the Czech Republic
- Medicinal preparations in Prague pharmacies at the end of the 16th century
- Therapeutic potential of phytocannabinoids and synthetic derivatives affecting human endocannabinoid system
- Characterization of celluloses by means of viscoelastic parameters
- Czech and Slovak Pharmacy
- Journal archive
- Current issue
- Online only
- About the journal
Most read in this issue- History and the present state of hypolipidaemic therapy
- Effect of montelukast on the treatment of asthma bronchiale in pediatric patients with perennial allergic rhinitis
- Medicinal preparations in Prague pharmacies at the end of the 16th century
- Impact of demographic factors on consumption of pharmaceuticals in the Czech Republic
Login#ADS_BOTTOM_SCRIPTS#Forgotten passwordEnter the email address that you registered with. We will send you instructions on how to set a new password.
- Career