-
Medical journals
- Career
Pulmonary fluid accumulation and its influence on the Impedance Cardiogram: CompariSON Between a Clinical Trial AND FEM Simulations
Authors: Mark Ulbrich 1; Jens Mühlsteff 2; Matthias Daniel Zink 3; Fabienne Wolf 3; Sören Weyer 1; Thomas Vollmer 4; Stefan Winter 4; Steffen Leonhardt 1; Marian Walter 1
Authors‘ workplace: Philips Chair for Medical Information Technology, RWTH Aachen University, Aachen, Germany 1; Philips Research, Eindhoven, The Netherlands 2; Dept. of Cardiology, Pneumology, Angiology and Intensive Care Medicine, RWTH University Hospital Aachen, Germany 3; Philips GmbH Innovative Technologies, Aachen, Germany 4
Published in: Lékař a technika - Clinician and Technology No. 4, 2014, 44, 28-34
Category: Original research
Overview
Impedance cardiography (ICG) is a simple and non-invasive method to assess hemodynamic parameters which, so far, unfortunately fails to provide accurate measurements in patients with heart failure. This study aimed to identify reasons for the inability of ICG to assess hemodynamic parameters in patients with lung edema or pleural effusion. For this, finite element simulations were conducted using a simplified simulation model based on human MRI data. This model includes volumetric changes of heart beat and aortic expansion, as well as changes during lung perfusion and erythrocyte orientation. To simulate fluid accumulations, lung tissue was stepwise substituted by body fluid. Moreover, the whole lung, as well as the left lung and right lung affected by fluid accumulation, were analyzed to establish their influence on the impedance cardiogram; the impact of changes in position was also included in the analysis. The results show a similar decrease of calculated and extracted values in all simulated measurement scenarios. In addition, the trend of these values was verified by means of a clinical trial. Using echocardiography, we confirmed that current models estimating stroke volume cannot be applied in patients with heart failure and with lung edema or pleural effusion.
Keywords:
bioimpedance, impedance cardiography, echocardiography, heart failure, pleural effusion, lung edema, recompensation, stroke volumeIntroduction
In Western Europe, the steadily aging society will pose increasing challenges on the healthcare systems. For example, the prevalence of age-related diseases will increase significantly whereas medical facilities will suffer from insufficient medical staff [1]. One of these diseases is heart failure (HF); the prevalence of HF in developed countries is about 2% and is about 10-20% among elderly persons aged ≥ 70 years. The diagnosis and treatment of HF is costly and the disease itself is associated with increased morbidity and mortality [2]. However, improved quality of life and life expectancy could be achieved with early diagnosis and treatment. The diagnosis usually comprises many different modalities for the classification and visualization of HF; this generally involves a con-siderable number of medical staff, as well as costly medical devices and treatments. In practice, early diagnosis is not possible since this usually takes place after a patient has been admitted to hospital with symptoms of HF.
Impedance cardiography (ICG) might be a valuable method to enable early diagnosis of decompensation among elderly persons, since this technique is inex-pensive, non-invasive and easy to use. It can be used in a home healthcare setting as an early warning system; moreover, no medical staff is required to perform the measurements. Unfortunately, however, ICG method is currently not considered to be reliable when monitoring patients with heart-related diseases [3] [4].
In this study, finite element method (FEM) simulation was used to identify factors that influence impedance measurements in patients with HF, in order to explain the reasons for inaccurate ICG measure-ements in this group. In addition, patients with HF were monitored during their recovery phase in hospital to analyze whether ICG is able to monitor the recovery process and verify the simulations.
Basics
Impedance cardiography
ICG is a non-invasive bioimpedance measurement technique used to assess hemodynamic parameters by means of standard adhesive surface electrodes (Ag/AgCl) placed on the neck over the carotid arteries and along the midaxillary line at the level of the xiphoid process (Fig. 1).
Fig. 1: Standard ICG electrode positions. 
To measure the impendance, a small alternating current is injected into the body by one pair of electrodes and the voltage drop over the area of interest is measured by another pair of electrodes. In this way, the continuous absolute bioimpedance at one frequency can be obtained by means of Ohm’s law:
Using the temporal derivative of the continuous impedance (|dZ(t)/dt|), characteristic points associated with physiologic events can be extracted (Fig. 1):
Fig. 2: Temporal derivative (ICG) of the measured bioimpedance with its characteristic points. 
The characteristic points of this derivative are associated as follows [5]:
- B: Opening of the aortic valve
- C: Maximal mechanical contraction
- X: Closure of the aortic valve
- O: Opening of the mitral valve
This information can be used to calculate the left ventricular ejection time (tLVET), which is defined as the time difference between point B and point X and, consequently, the stroke volume (SV) [6]:
This equation was introduced by Bernstein and Sramek in 1986 Chyba: Zdroj odkazu nenalezen. It includes a factor δ = (BMI/24 kg m−2)-2 defined as a constant proportional to the ratio of the patient’s body mass index (BMI) and the ideal BMI (24 kg m−2). H is the patient’s height and Z0 the static base impedance (offset of the continuous impedance).
Heart failure
Heart failure is a clinical syndrome describing a state in which the heart is unable to pump sufficient blood to the periphery to supply the organs [8]. HF often develops after other conditions have damaged or weakened the heart, such as atherosclerosis, myocardial infarction or hypertension; all these may lead to a cardiomyopathy. HF can be differentiated into left and right HF. An impaired pumping function of the left ventricle causes lung edema, whereas right HF generates excess fluid accumulation in the whole body and the periphery. Pleural effusion is excess fluid accumulation in the cavity between the lung and thoracic wall (pleura). It is similar to edema and can therefore be called ‘edema of the pleural cavity’. Although pleural effusion can develop due to left or right HF, it is more commonly observed in patients with biventricular HF [9]. Classification of the extent of HF can be made using the New York Heart Association (NYHA) functional classification (Tab. 1) as follows:
1. NYHA classification of the stages of HF [10]. ![NYHA classification of the stages of HF [10].](https://www.prolekare.cz/media/cache/resolve/media_object_image_small/media/image/c449510b641c28a54d77237b92a07312.png)
Basic treatment of HF is based on a change of lifestyle by reducing cardiovascular risk factors such as smoking, hyperlipidemia, hypertension, diabetes and overweight, as well as reducing dietary salt intake, getting daily physical activity, and use of medication to reduce high blood pressure and fluid retention. In the case of hospitalization due to acute HF, medication is used to remove excess fluid and achieve hemodynamic stabilization of the patient. Moreover, medical devices can be applied, such as left ventricular assist devices or a total artificial heart which temporarily supports the heart until transplantation. Cardiac transplantation is required for patients with end-stage HF (requiring a heart from a human donor).
Methods
To analyze the influence of fluid accumulation in the thorax on the impedance cardiogram, an appropriate FEM model for simulations was created. In addition, to validate the simulations, ICG was measured in patients with HF suffering from these symptoms. The simulation setup and the trial protocol are described below.
FEM simulations
To conduct FEM simulations, a FEM model is required that provides geometries resembling the shapes and organs of the human thorax. In addition, its temporal resolution must be high enough to analyze the influence of pathologies on time-dependent hemodynamic parameters, such as tLVET. As a geometric basis, MRI data of a human male served as an anatomic template. Simple geometric shapes (such as cylinders, frustums and spheres) were used to represent important organs of the thorax. This approach reduces computational time and enables to easily include geometric changes of organs to simulate physiological or pathophysiological changes. The dynamic changes implemented in this model are: aortic expansion, erythrocyte orientation, lung perfusion, and heart contraction. This FEM model produces excellent correlations with measured signals and is robust to conductivity changes of tissues and organ displacements [11].
To simulate a fluid accumulation, lung tissue was stepwise substituted by body water. Four scenarios were simulated: fluid accumulation in both lungs, as well as in the left lung and right lung (all in upright position). In addition, simulations with body fluid in both lungs in supine position were conducted, assuming that the fluid accumulation occurs primarily in the dorsal region of the lung The simulation software was CST EM Studio from Computer Simulation Technology (Darmstadt, Germany); this was used to compute the simulations on a personal computer with a 64 bit operating system, an Intel Xeon R 5240 processor with 2 cores and 24 GB RAM. The low frequency electroquasistatic solver (electroquasistatic Maxwell’s equations) was employed and each model was composed of 1.5 million tetrahedrons.
Instead of injecting a current and measuring the voltage, a voltage was defined and the total current I calculated by integrating the current density J and the electric displacement field D as follows:
Fig. 3 shows the simulation model in frontal view with lung (85% filled with body fluid), heart and aorta highlighted:
Fig. 3: Simulation model showing 85% of lung tissue substituted with body water (upright position). 
Clinical trial
Since it was thought not to be feasible to monitor patients at home whilst waiting for decompensation and hospitalization in the presented clinical trial, ICG was measured during an approximation of the ‘reverse process’ of decompensation (Ethical Committee approval no. NCT01775306, dated 29 September 2011). Decompensated HF patients were treated in hospital, mainly by ingestion of diuretics, normalizing heart-related parameters and leading to a reduction in body fluid to normal levels. As a result, this could lead to increased hemodynamic performance of the heart. Patients were requested to participate for at least 4 days in the study but, ideally, for their entire stay in the hospital. For the present trial, 46 patients with HF (males and females) were enrolled. Exclusion criteria were implants (such as pacemakers) or pregnancy. ICG was measured using standard electrode positions (Fig. 1). To keep other parameters influencing the impedance measurements as constant as possible, several measures were taken. The patient’s skin was cleaned with an antiseptic agent (based on alcohol) at the electrode positions to remove fat and other substances that might influence the skin-electrode interface impedance, and to ensure good adhesion of the electrodes. In addition, room temperature and air humidity were kept as constant as possible. Patients were measured each morning in the same position before getting up in order to exclude fluid redistribution in the body from the measurements. Nevertheless, because of the clinical routines, data of only 7 patients could be used due to, for example, other clinical examinations, patient transfers, or faulty measureements. Another reason is that the echocardi-ography data of only one third of the patients was of a sufficiently good quality to reliably assess the left ventricular SV.
In addition, a transthoracic echocardiogram (TTE) was assessed in apical four-chamber view to subsequently calculate the SV using the monoplane Simpson method. This method is used to estimate the left ventricular end-diastolic volume (EDV) and end-systolic volume (ESV) using the following equation:
In general, the volume V is calculated by subdividing the ventricle into i cylindrical slices with the radius ai. Here, L is the length of the ventricle between the mitral valve and the apex. The SV is then EVD-ESV [12].
Results
For every filling stage of the lung, 103 simulations were conducted, resulting in 1648 simulations for all scenarios. Fig. 4 shows simulated impedance curves with offset correction (|Z(t) − Z0|) for healthy state (0% filling) and for all filling stages; their behavior is representative for all simulated scenarios. Note that the SV ejected by the heart was kept constant for all filling stages.
Fig. 4: Simulated offset-corrected impedance curves of the thorax as a function of different filling stages of the lung. 
It can be seen that the peak-to-peak impedance Zpp decreases with increasing filling stage (maximum -54%). In addition, the morphology remains almost constant, so that no significant changes in tLVET can be assumed.
Fig. 5: Temporal derivatives of the simulated impedances with different filling stages of the lung. 
This impression is confirmed by the ICG curve (Fig. 5 showing no significant shift of characteristic points. In addition, the maximum of the ICG curve also decreases for each increasing filling stage (maximum -35%). Tab. 2 summarizes extracted values from the simulation results, assuming an upright position.
2. Simulation results for upright position. Analyzed values for each filling stage with whole lung fluid accumulation (upper half) and deviations for left side fluid accumulation (lower half). 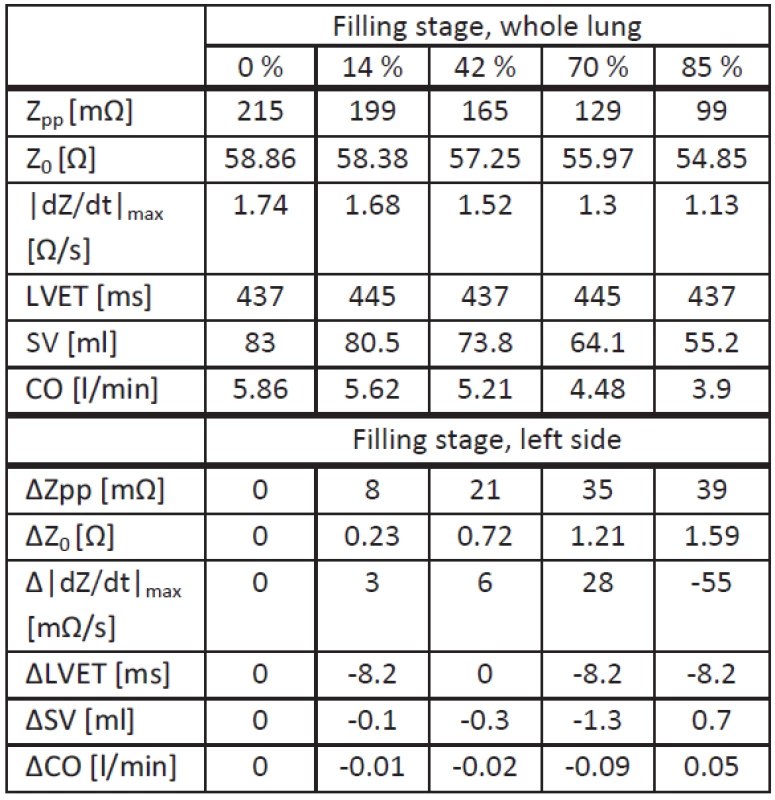
Note that here the X point was assumed to be the local minimum after the C point, and the B point the local minimum before the C point.
The upper half of Tab. 2 shows the values from simulations with whole lung fluid accumulation, and the lower half shows deviations from these values obtained with simulations with fluid accumulation at the left side. Comparing both scenarios, there are no significant differences in the behavior of tLVET or Z0, leading to a maximal SV difference of 1.3 ml. Concerning Zpp its decrease due to left side fluid accumulation is lower (maximum -36%). Right lung fluid accumulation show the same behavior as left lung fluid accumulation, despite an identical |dZ(t)/dt|max compared to whole lung fluid accumulation. The decrease for this value is higher with persistent left lung fluid accumulation (maximum -38%).
To establish whether the patient’s position has an influence on the ICG measurement, whole lung fluid accumulation simulations were compared in upright and supine position. Tab. 3 summarizes extracted and calculated parameters.
3. Simulation results for supine position. 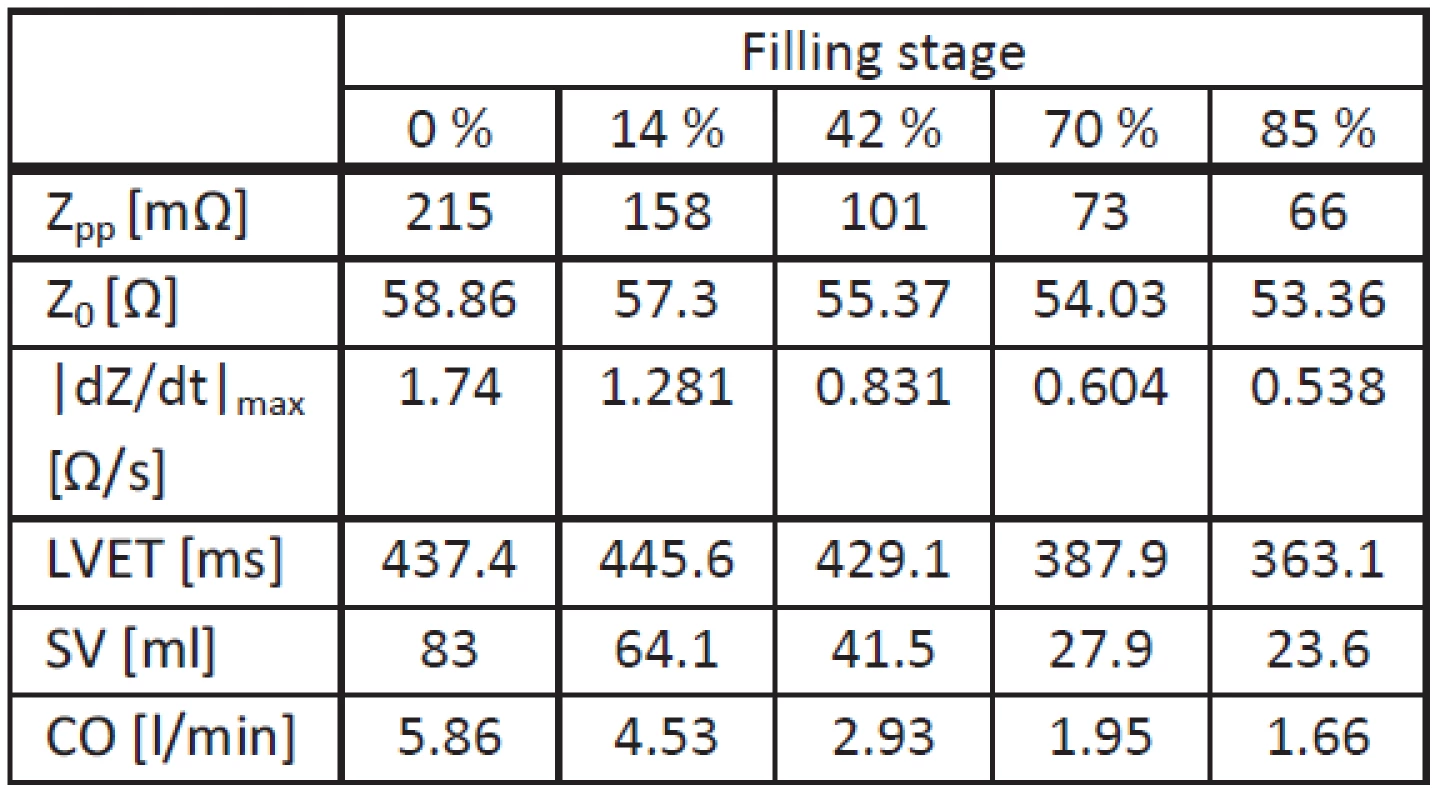
In supine position, all values (including tLVET) decrease with increasing filling stage. In addition, |dZ(t)/dt|max and Zpp show a higher decrease compared with the upright position. As a consequence, the SV decrease due to fluid accumulation is higher.
To summarize, a decrease of Zpp and Z0 is seen in all simulated scenarios influencing the calculated SV. In addition, it is seen that the injected current tends to flow through the well-conducting tissue with fluid accumulation. This is shown in Fig. 6 for left lung fluid accumulation:
Fig. 6: Simulated left lung fluid accumulation showing rerouted current flow. 
Here, the accumulation of lung fluid is shown in blue and the unaffected lung tissue in pink.
To verify whether these findings are congruent with measurements in clinical practice, the data of patients with HF were analyzed. Fig. 7 presents the measured impedance curves for one representative patient.
Fig. 7: Example of measured offset-corrected impedance curves of the thorax with different filling stages of the lung. 
This patient (age: 87 years, weight: 60 kg, height: 160 cm) was admitted to hospital with dyspnea under physical stress and valvular aortic stenosis (NYHA III-IV). He had pleural effusions affecting both lungs, which disappeared after treatment. The patient was monitored 7 times during his 9-day stay in the hospital. As shown in Fig. 7, Zpp increases with each day of measurement (equal to maximum -66%) as does (equal to maximum -66%). Interestingly, this behavior was observed only in patients with pleural effusion.
To evaluate the reliability of the bioimpedance measurements for patients showing the above-mentioned behavior, the temporal development of SV measured on echocardiography and with ICG was compared (Fig. 8).
Fig. 8: Stroke volume estimated on echocardiography (green) and on impedance cardiography (blue). 
Fig. 8 shows that SVs estimated with echocardiography and with ICG are not correlated (r=0.0675).
Conclusion
In this study, an FEM model of the human thorax was used to simulate thoracic bioimpedance for patients with HF and with accumulation of fluid affecting the lung. A model was created with the required dynamic sources with a high temporal resolution resulting in impedance curves which can be used to extract hemodynamic parameters. In this model, lung tissue was stepwise substituted with body fluid to simulate fluid accumulation in the lung resulting from lung edema or pleural effusion. The results show decreasing amplitudes of the impedance curve, the ICG curve and the base impedance. Similar results were obtained when comparing the whole lung, as well as accumulation of fluid in the left and right lung. The altered impedance dynamics is most likely caused by rerouting the injected current away from the blood-filled vessels and from the heart by fluid accumulation. This allowed to identify one reason for the inaccurate ICG measurements in patients with HF.
In addition, reference measurements using echocardiography show that the SV estimated by ICG does not correlate with the actual SV and can, therefore, be considered to be incorrectly estimated due to the patient’s pathology. Together with the findings from bioimpedance simulations and measurements (showing a decrease of Zpp and Z0), and the current flow visualized through tissue with fluid accumulation, this is another indication for a rerouting of the injected current leading to a misinterpreted SV on ICG.
In conclusion, current models for the estimation of SV with ICG cannot be applied in patients with HF since they cannot compensate a disproportionately high increase in tissue conductivity in the thorax. They will need to be modified. In addition, since deviations were observed concerning the trend of simulated values with altered body position, actual measurements should be performed using a standardized scenario.
Acknowledgements
The project was selected under the operational program co-financed by the European Regional Development Fund (ERDF) Objective 2 ’Regional Competitiveness and Employment’ (2007-2013), North Rhine-Westphalia, Germany and was partly supported by Philips Research Europe, Eindhoven, The Netherlands.
Mark Ulbrich
Philips Chair for Medical Information Technology
RWTH Aachen University
Pauwelsstrasse 20, D-52074 Aachen
E-mail: ulbrich@hia.rwth-aachen.de
Phone: +49 241 8023201
Sources
[1] Peter, W. F., Wilson, P. W. F., D’Agostino, R. B., Sullivan, L., Parise, H., and Kannel, W. B. Overweight and obesity as determinants of cardiovascular risk: the Framingham experience. Arch Intern Med, 2002, vol. 162, no. 16, p. 1867-1872.
[2] Dickstein, K., and Authors/Task Force Members. ESC Guidelines for the diagnosis and treatment of acute and chronic heart failure 2008. European Journal of Heart Failure, 2008, vol. 10, p. 933-989.
[3] Raaijmakers, E., Faes, T. J., Scholten, R. J., Goovaerts, H. G., and Heethaar, R. M. A meta-analysis of three decades of validating thoracic impedance cardiography. Critical care medicine, 1999, vol. 27, p. 1203-1213.
[4] Cotter, G., Impedance cardiography revisited, Physiological Measurement, 2006, vol. 27, p. 817-827.
[5] Summers, R. L., Shoemaker, W. C., Peacock, W. F., Ander, D. S., and Coleman, T. G. Bench to bedside: Electrophysiologic and clinical principles of noninvasive hemodynamic monitoring using impedance cardiography. Academic Emergency Medicine, 2003, vol. 10, p. 669-680.
[6] Bernstein, D. P., and Lemmens, H. J. M. Stroke volume equation for impedance cardiography. Medical & Biological Engineering & Computing, 2005, vol. 43, p. 443-450.
[7] Bernstein, D. P. A new stroke volume equation for thoracic electrical bioimpedance: theory and rationale. Critical Care Medicine, 1986, vol. 14, p. 904-909.
[8] McMurray, J. J. V., and Pfeffer, M. A. Heart failure. Lancet, 2005, vol. 365, no. 9474, p. 1877-1889.
[9] Porcel J. M., Light, R. W. Diagnostic approach to pleural effusion in adults. American Academy of Family Physicians, 2006, vol. 73, p. 1211-1220.
[10] The Criteria Committee of the New York Heart Association. (1994). Nomenclature and Criteria for Diagnosis of Diseases of the Heart and Great Vessels. (9th ed.). Boston: Little, Brown & Co. pp. 253–256.
[11] Ulbrich, M., Mühlsteff, J., Leonhardt, S., and Walter, M. Influence of physiological sources on the impedance cardiogram analyzed using 4D FEM simulations. Physiological Measurement, 2014, vol. 35, no. 7, p. 1451-1468.
[12] Flachskampf, F.A., Kursbuch Echokardiographie, Thieme, 2006.
Labels
Biomedicine
Article was published inThe Clinician and Technology Journal

2014 Issue 4-
All articles in this issue
- Solution of the Cross-talk problem in cell impedance analysis of cardiac myocytes
- Differences in sleep patterns among healthy sleepers and patients after stroke
- EFFECT OF THE PLACEMENT OF THE INERTIAL SENSOR ON THE HUMAN MOTION DETECTION
- Impact of different heart rates and arterial elastic moduli on pulse wave velocity in arterial system model
- Pulmonary fluid accumulation and its influence on the Impedance Cardiogram: CompariSON Between a Clinical Trial AND FEM Simulations
- REAL-TIME visualization of multichannel ECG signals using the parallel CPU threads
- The Clinician and Technology Journal
- Journal archive
- Current issue
- Online only
- About the journal
Most read in this issue- REAL-TIME visualization of multichannel ECG signals using the parallel CPU threads
- Differences in sleep patterns among healthy sleepers and patients after stroke
- Pulmonary fluid accumulation and its influence on the Impedance Cardiogram: CompariSON Between a Clinical Trial AND FEM Simulations
- EFFECT OF THE PLACEMENT OF THE INERTIAL SENSOR ON THE HUMAN MOTION DETECTION
Login#ADS_BOTTOM_SCRIPTS#Forgotten passwordEnter the email address that you registered with. We will send you instructions on how to set a new password.
- Career





