-
Medical journals
- Career
Determination of Human Gait Phase by Zero-moment Point
Authors: Slavka Viteckova 1; Patrik Kutilek 1; Zdenek Svoboda 2; Jan Kauler 1; Marcel Jirina 1
Authors‘ workplace: Czech Technical University in Prague, Faculty of Biomedical Engineering, Kladno, Czech Republic 1; Palacky University in Olomouc, Faculty of Physical Culture, Olomouc, Czech Republic 2
Published in: Lékař a technika - Clinician and Technology No. 3, 2012, 42, 21-24
Overview
This paper discuss approach to gait phase determination via fuzzy inference. The stability criteria applied to biped robots, namely Zero Moment Point (ZMP) have been employed. Designed fuzzy inference system uses data about the ZMP position. Gait phase is the output of our fuzzy system. Simplified human body model is introduced for computation of ZMP. Both inter - and intra-subject phase identification are examined. The developed fuzzy-rules based system is exemplified to show capability of different subjects gait data generalization. Results of designed fuzzy IF-THEN rules based system show that the proposed method is suitable for this type of task.
We designed system to identify gait phases, which could potentially help to assess the quality of walking. Although the method for studying ZMP in combination with fuzzy logic could contribute to the design of new prosthesis and the diagnosis of disorders, this issue has not been systematically studied in the past.Keywords:
gait phase, gait modeling, ZMP, zero-moment pointIntroduction
Many proposals attempt and full implementation to create human exoskeleton have been done. Exoskeletons are human oriented robots which run in parallel with the operator. We focused to those exoskeletons which are aimed to human lower extremities. This class of robots is used to assist the operator, support for ADL (Activities of Daily Life) or assist during rehabilitation process.
Control of such devices is complex task that uses information from various sensors (EMG, pressure, force sensors, accelerometers, gyroscopes, potentiometers, etc.) placed directly on operator or exoskeleton's construction.
To get operator's movement the BLEEX (Berkeley Lower Extremity EXoskeleton) [1] utilizes 45 sensors. The BLEEX actively supports 4 DoFs (Degree of Freedom) per limb (hip flexion/extension, hip abduction/adduction, knee and ankle flexion/extension) and was developed to strengthen an full body of operator.
For support of operator's weakened body, mobility and ADL the exoskeleton HAL (Hybrid Assistive Limb) [2] was developed. HAL uses EMG sensors, GRF sensors, potentiometers, gyroscopes and accelerometers. Informations obtained by the sensors are inputs to control systems which allows actively control the movement in hip and knee (both flexion/extension). The latest HAL version (no. 5) can be worn by single right/left medial part of the body [3].
Above mentioned robotic devices and most other require both fully or partially functional both lower extremities (except HAL-5). This is because that data from sensors are used to control ipsilateral lower limb (including HAL-5).
Such exoskeletons need accurate input signal processing to identify the type of operator's movement and to infer the necessary robotic's action. Crucial issue of lower limbs exoskeletal devices is stability determination. The stability criteria applied to biped robots, namely Zero Moment Point (ZMP), and its relation to human gait have been investigated previously [4]. Dynamic stability depends on the area of support polygon, and thus it is dependent on gait phase. That is why gait phase detection is important step to determine the stability. We employed artificial intelligence to gait phase determination.
At present, typical application areas of fuzzy logic are in process control, classification and pattern recognition. Fuzzy systems hallmark is the use of human empirical knowledge.
This paper is organized as follows. Next section describes the measured subjects (participants) and the process of data acquisition. Further it explains zero moment point, its importance and computation. Results and description of proposed fuzzy inference system are stated in section Application of the Method and Results. Finally, summary and concluding remarks are placed in the last section.
Methodology
Participants
Gait data was collected from 3 healthy subjects (2 male, 1 female) who were 31-49 years of age. The subjects had no prior gait disabilities. In the experiment, each participant was required to walk five successive trials under different walking speed. In each trial, data from the first two gait cycles for acceleration and two last gait cycles for deacceleration were excluded. Then, four gait cycles of the rest of acquired gait data were selected for analysis. It yielded a total number of 12 gait cycles for different speeds of all participants. We assume that the number is sufficient for a preliminary verification of the basic design of our fuzzy system.
Data Acquisition
In order to develop and verify predictive system the kinematic data of both lower limbs need to be recorded, especially data to determination of hip, knee, ankle and torso positions. While there are several different methods for capturing and extracting the desired joint positions, the accurate Vicon motion capture system sampled at 200 Hz was used. The location of markers followed Vicon marker set placement recommendation. Positions of the markers on the subject used to ZMP computation were as follows: seventh cervical vertebrae, left knee, left ankle, right knee, right ankle and lowest points of anterior superior iliac spines.
Zero-Moment Point and its Significance
Term Zero-Moment Point (ZMP) is the known and frequently used to control and planning bipedal robot movement. ZMP is the criterion of dynamic equilibrium.
The concept of ZMP is known to the scientific community since 1972, when it was first introduced by Miomir Vukobratovic [5]. Later, Goswami [6, 7] published a critical look at the ZMP, compared ZMP with the COP (Center of Pressure), extended the description of ZMP and thereby defined a new indicator of stability - FRI (Foot Rotation Indicator). In subsequent works Vukobratovic summarized the history of ZMP, emphasized the fundamental importance of the relationship illustrated ZMP and COP, and exactly defined the terminology used in the synthesis walk [8, 9].
To maintain subject's dynamic equilibrium the GRF (Ground Reaction Force) should act on the foot, so that all the forces acting on the body (inertia, gravity, centrifugal, Coriolis forces and the corresponding moments) remain balanced. If the coordinate system origin is located just to this GRF point, it is clear (from equilibrium conditions) that all moments acting around the horizontal axis (x and y) are equal to zero. According to this basic knowledge the point where the GRF acts on the foot is called ZMP.
FZMP (Fictitious ZMP)
As written above, there may be cases where the ZMP does not fall within the support polygon. Then, this point is called FZMT (Fictitious ZMP), also known as IZMP (Imaginary ZMP) and FRI (Foot Rotation Indicator [6, 7]). This is not a real ZMP, but the hypothetical point where the ZMP would be placed, if the support polygon was large enough.
Equations of ZMP/FZMP
From the basic knowledge of the ZMP several equations [10, 11] for the calculation of it were derived. Components of ZMP position can be calculated from equations (1) and (2). Detailed derivation of the calculation mentioned below can be found in [11].
where mtot is total mass, pCoMxand pCoMy mean components of pCoM; distance from the base-frame-origin to CoM, g is gravitational acceleration, Ṕz is z-component of time derivative of total linear momentum P, Ḣx and Ḣy are components of time derivative of total angular momentum H. For simplicity, component zZMP is assumed to be zero.
Calculation of total angular momentum is stated in (3).
where pi is distance from the base-frame-origin to CoM of i-th link, mi is mass of i-th link, H are inertia tensors i-th link, ωi is angular velocity of i-th link.
Calculation of total linear momentum P is stated in (4).
Application of the Method and Results
Simplification of human body structure had to be done to achieve less-time consuming calculation of ZMP. A kinematic model of human body is presented in Fig. 1. A simplified model is in the form of 6-element kinematic chain with 7 DoF. Head, arms and trunk were replaced by single rod whose mass is equal to the sum of masses of all its parts. The legs are without feet, shanks and thighs are replaced by rods too. Anthropomorphic data from standard tables were used to determine the mass fractions and the locations of the centers of mass of each body segment [12]. Origin of the Cartesian coordinate system is set to pelvis.
Fig. 1: Simplified kinematic model of human body. View in sagittal plane (left), view in frontal plane (right). Centers of mass are marked by orange circles. 
We derived the appropriate inertia tensor for each segment. A sample calculation of thigh inertia tensor is shown in (5), (6).
In order to identify human gait phase, the FIS (fuzzy inference system) with a Mamdani fuzzy IF-THEN inference mechanism was used. Input variables were time series of ZMP x-component, which were computed as discussed in previous section. Based on the knowledge that the shape of the ZMP curve varies among subjects and a curve can be shifted up or down (Fig. 2) we did not use any specific value to describe the position of ZMP. Instead, we used only the differences between the values i.e. ZMP x-components. Firstly, the fuzzyfication of each input variable has been done.
Fig. 2: Example of ZMP x-component and the time series of value differences. 
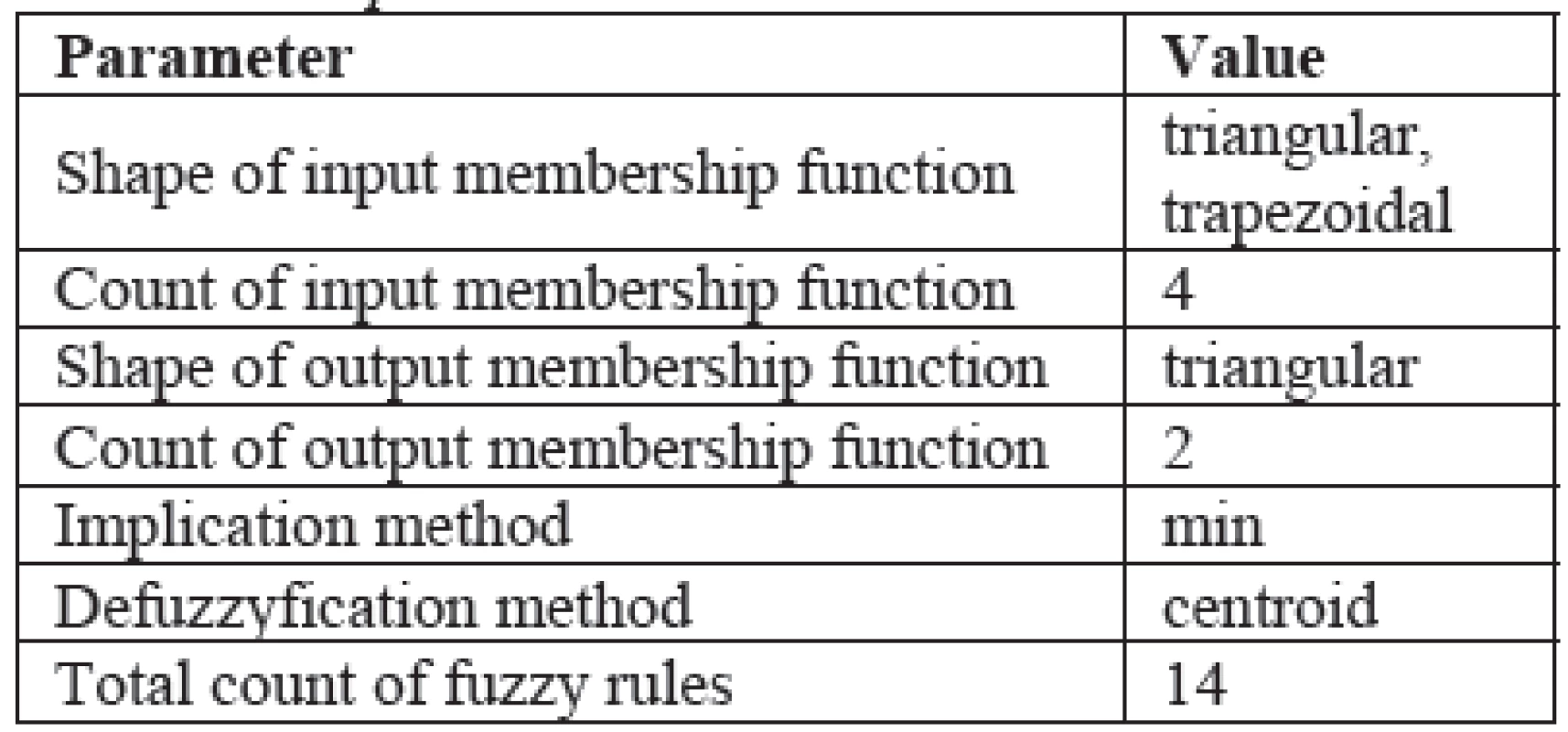
We used the Fuzzy Toolbox in MatLab to create the Mamdani Fuzzy Inference System. Parameters of developed FIS are summarized in the Table 1.
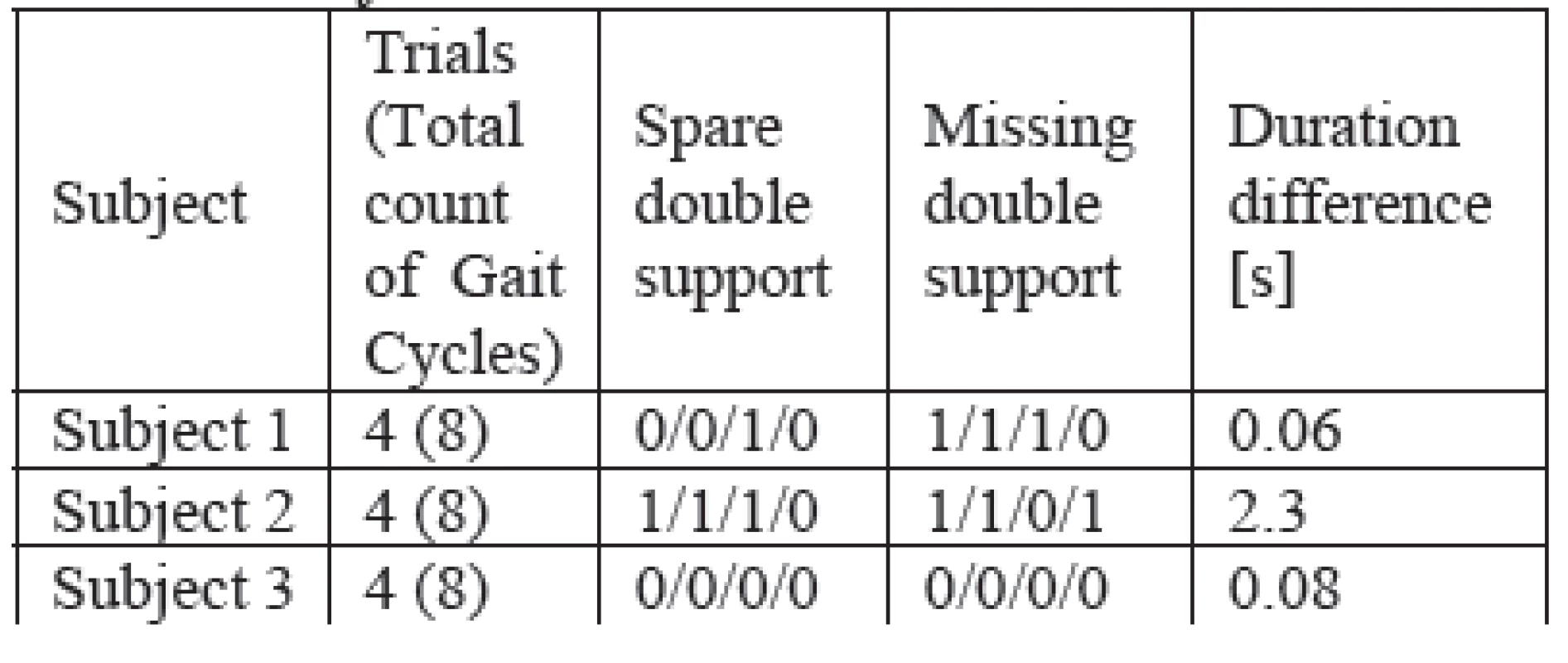
To verify the correct function of the designed FIS, we identified double support phases of four gait cycles of each subject (without prior knowledge of subject's ZMP x-component). Verification results of one trial for Subject 2 are graphically represented on Fig. 3. To evaluate the results we considered total count of spared double support phases, total count of missing double support phases and average difference in actual and identified double support phases duration as suitable parameters. Table 2 summarizes achieved results of each subject (notation explanation: Spare souble supp. cells and Missing double supp. cells contain 4-touples which mean <1st trial/2nd trial/3rd trail/4th trial>).
It can be seen that both the human and FIS predictions of the double/single support phase are in line with actual double/single support phases. Also, note that the double support phase duration is shorter the expected value for a normal gait cycle. For each of the other gait phase transitions, the FIS predictions are in-line with those made by human reasoning. In order to prevent any possible bias, the human analysis was performed before the FIS system was employed.
Verification result of Subject 2, trial 1. 
Conclusion
Human gait is quasi-periodic and similar among people. Therefore techniques of artificial intelligence seem to be very suitable to determination of human lower limbs movement's parameters.
Utilizing reflexive markers approach we obtained kinematic human body data during walking. We reasonably simplified human body model and computed zero moment point based on measured data. Then we designed fuzzy inference system for gait phase detection. ZMP time series are input to the designed system and information about the gait phase was the output.
Our new intelligent system can become new system for gait stability assessment. Further, this approach of quantitative assessment gives us new methods and algorithms which can be used to control robotic devices such as rehabilitation and assistive orthotics devices of lower limbs. Together with control of robotic lower limbs devices this system is intended to be used for gait planning and lower limbs movement synthesis.
Our future work will extend current system for gait phase identification to enable the identification of dynamic stability. Moreover, we consider computation of the ZMP acceleration to identify the control data to robotic lower limb actuators. It can be done via artificial intelligence too. In this case it will be necessary to take into account the loss of precision of the calculation and acceptable ratio between acceleration of calculation and loss of precision must be found. For this reason, our article shows only the beginning of our more complex work, and in this article, we primarily show the potential of our proposed method.
Acknowledgement
We acknowledge the support of the Grant No. SGS12/206/OHK4/3T/17.
Slávka Vítečková
Katedra biomedicínské informatiky
Fakulta biomedicínského inženýrství
České vysoké učení technické v Praze
nám. Sítná 3105, CZ-272 01 Kladno
E-mail: slavka.viteckova@fbmi.cvut.cz
Sources
[1] Zoss, A. and Kazerooni, H. (2006). Design of an electrically actuated lower extremity exoskeleton, Advanced Robotics, 20(9), 967-988.
[2] Kawamoto, H., Lee, S., Kanbe, S., and Sankai, Y. (2003). Power assist method for HAL-3 using EMG-based feedback controller, 2(), 1648-1653.
[3] Kawamoto, H., Hayashi, T., Sakurai, T., Eguchi, K., and Sankai, Y. (2009). Development of single leg version of HAL for hemiplegia, , (), 5038-5043.
[4] Mrozowski, J., Awrejcewicz, J., and Bamberski, P. (2007). Analysis of stability of the human gait, JOURNAL OF THEORETICAL AND APPLIED MECHANICSWARSAW, 45(1), 91.
[5] Vukobratović, M. and Stepanenko, J. (1972). On the stability of anthropomorphic systems, Mathematical Biosciences, 15(1-2), 1-37.
[6] Goswami, A. (1999). Postural Stability of Biped Robots and Foot Rotation Indicator (FRI) Point, International Journal of Robotic Research, 18(6).
[7] Goswami, A. (1999). Foot-Rotation Indicator (FRI) Point: A New Gait Planning Tool to Evaluate Postural Stability of Biped Robots, , (), 47-52.
[8] Vukobratović, M., Borovac, B., and Šurdilović, D. (2001). Zero-Moment Point - Proper Interpretation and New Applications.
[9] Vukobratović, M. and Borovac, B. (2004). ZERO-MOMENT POINT - THIRTY FIVE YEARS OF ITS LIFE, International Journal of Humanoid Robotics.
[10] Huang, Q., Yokoi, K., Kajita, S., Kaneko, K., Arai, H., Koyachi, N., and Tanie, K. (2001). Planning Walking Patterns for a Biped Robot, IEEE Transactions on Robotics and Automation, 17(), 280-289.
[11] Dekker, M. H. P. (2009). ZERO-MOMENT POINT METHOD FOR STABLE BIPED WALKING.
[12] Winter, D. A. (2005). Biomechanics and Motor Control of Human Movement.
Labels
Biomedicine
Article was published inThe Clinician and Technology Journal

2012 Issue 3-
All articles in this issue
- Physical Activity Prescription Based on Stress Test Examination
- ECMO ambulance and advanced emergency medical system
- Measurement of thermal symmetry of the human spine by the use of medical thermography
- Determination of Human Gait Phase by Zero-moment Point
- Leksell gamma knife past, present and future
- The Clinician and Technology Journal
- Journal archive
- Current issue
- Online only
- About the journal
Most read in this issue- Leksell gamma knife past, present and future
- Physical Activity Prescription Based on Stress Test Examination
- Measurement of thermal symmetry of the human spine by the use of medical thermography
- ECMO ambulance and advanced emergency medical system
Login#ADS_BOTTOM_SCRIPTS#Forgotten passwordEnter the email address that you registered with. We will send you instructions on how to set a new password.
- Career