-
Medical journals
- Career
- Contact
PERISTALTIC FLOW OF LITHOGENIC BILE IN THE VATERI’S PAPILLA AS NON-NEWTONIAN FLUID IN THE FINITE-LENGTH TUBE: ANALYTICAL AND NUMERICAL RESULTS FOR REFLUX STUDY AND OPTIMIZATION
Authors: Alex Kuchumov 1; Vadim Tuktamyshev 1; Marat Kamaltdinov 2
Authors‘ workplace: Department of Theoretical Mechanics and Biomechanics, Perm National Research Polytechnic University, Perm, Russia 1; Federal Scientific Center for Medical and Preventive Health Risk Management Technologies, Perm, Russia 2
Published in: Lékař a technika - Clinician and Technology No. 2, 2017, 47, 35-42
Category: Original research
Overview
Bile is one of 32 bio-fluids in the human body. Lithogenic bile (bile with tendency for the gallstones formation) is the pathological state of bile. Rheological properties of lithogenic bile differ from normal one. The Vateri’s papilla is the narrowest duct in the biliary system. Peristaltic motion plays important role in the bile flow in the Vateri’s papilla. In the literature, there are many papers devoted to peristaltic flow of fluids in the infinite length tubes. There are not many papers devoted to peristaltic flow of fluids in the finite length tubes. Modelling of peristaltic flow in the finite length tubes requires the imposing of boundary conditions on the ends of a tube. It leads to problem statement complication and to obtain the problem solution is getting harder. The current paper aims at developing mathematical model of the peristaltic bile transport flow through the duct at papillary stenosis as a tapered finite-length tube. It allows evaluating velocities and pressure distribution along the tube, and detecting choledochopancreatic reflux occurrence conditions. Adopting the perturbation method, the analytical solutions for velocities and pressures are obtained. Pressure distribution versus axial coordinate at different time instants are plotted for various values of Weissenberg number and amplitude ratio. It revealed that the amplitude ratio has more effect on the pressure distribution along the tube compared to the Weissenberg number. The values of the pressure gradient corresponding to reflux occurring are obtained. The comparison between developed model and numerical peristaltic model code implemented in ANSYS was made. Moreover, it is reported that the pressure drop value corresponding to average flow rate equal to zero may serve as reflux occurrence criterion. Moreover, channel shape optimization was made for subsequent stent installation to restore normal bile flow using Nelder-Mead method.
Keywords:
tapered tube, finite length tube, peristalsis, Carreau fluid, bile, papillary stenosis, the Vateri’s papilla, duct shape optimizationIntroduction
Physiological motion of most of bio-fluids (blood, bile, urine) is related to wavy contraction of walls of hollow organs i.e. peristalsis [1–3].
To the date, there are number of papers devoted to peristaltic flow since first papers in 1960-s [4–8].
Also, some clue studies devoted to bio-fluid peristaltic transport can be highlighted in papers of Eytan et al [9], Jimenez-Lozano et al [10], Misra and Pandey [11–16], Rao et al [3, 17–19], Park et al [20].
The peristalsis flow of bile as Newtonian fluid in the common bile duct is studied in paper of Maiti and Misra [1]. It was found that reflux starts, when critical pressure is rather small, but the number of gallstones is rather big. The gallstones presence sufficiently decreases the flow velocity. Kuchumov et al [21] found that lithogenic bile behaves like a Carreau fluid and found constitutive parameters for the lithogenic bile.
There are several papers devoted to peristaltic flow of Carreau fluid in the tubes with various geometry.
Hakeem et al [22] presented results of Carreau fluid in the tube with a constant cross section. The analytical conditions of the separation in the flow were found using the boundary layer theory, namely, the trapping region at the wall decreases with increasing volume flow rate. Nadeem et al [23] studied the peristaltic Carreau fluid flow between two eccentric cylinders with moving inner cylinder; the obtained streamlines allowed to evaluate the trapping regions; analytical solution was obtained by the perturbation method. The velocity profiles and pressure gradient versus flow rate dependence were compared with the results of Mekheimer et al [24]. Hayat et al [25] investigated two-dimensional Carreau fluid flow in a symmetric channel at various kinds of waveforms by analogy with Hariharan et al paper [26], whom considered Bingham fluid flow in the tube with divergent walls.
This paper presents a technique, which can be applied for the stent installation into the stenosed duct. To increase the lumen of the duct, the stents should be inserted, but the stent choice is subjective because the surgeons do not know initial shape of the channel in the healthy state. So, they choose the stent basing on their experience.
Our approach is described as follows (Fig. 1). First of all, it is necessary to evaluate the current shape of patient’s stenosed duct in vivo. Secondly, we should evaluate bile flow dynamics in the duct based on mathematical model. Finally, it is necessary to find an optimal shape of the duct adopting Nelder-Mead method.
On the basis of the solved problems, one can obtain the optimal channel shape for the subsequent stent insertion to restore this shape for the normal flow dynamics.
Fig. 1: Proposed approach to stenosed duct study. 
Materials and methods
Anatomical background
Bile is the bio-fluid secreted by the hepatocytes (cells of the liver), which is responsible for the emulsification of fats [27]. From fluid mechanics point of view, bile flow depends on the pressure gradient and the wall contraction. Peristalsis plays an important role in the normal and pathological flows. Choledochopancreatic reflux (i.е. pathological flow of the gallbladder bile coming out the common bile duct into the pancreatic duct instead of the duodenum) is known to be one of the reasons of the pancreatitis (inflammation of the pancreas) [28]. The Vateri’s papilla is formed by the union of the pancreatic duct and the common bile duct. The ampulla is specifically located at the major duodenal papilla [29]. It is believed that hypomotility of sphincter of Oddi (muscular valve that controls the flow of bile and pancreatic juice through the ampulla of Vater into the duodenum) has an influence on the bile flow and reflux occurring [30]. Recently, it has been also discussed that changes in the structure and geometry of the Vateri’s papilla due to stone presence or papillary stenosis plays significant role in the reflux occurring [31].
Anatomy of bifurcation of common bile duct and pancreatic duct in the Vateri’s papilla ampoule surrounded by the Oddi’s sphincter is presented in Fig. 2 [32]. Papillary stenosis is the duct lumen decrease due to the scar tissue formation in the papilla [33].
Fig. 2: Anatomy of the biliary system including Oddi’s sphincter and ampulla of Vater (Vateri’s papilla) (Reprinted from https://commons.wikimedia.org, under CC BY license). 
Current stenosed shape evaluation
To evaluate the shape of stenosed duct of the real patient (male, 60 years) in vivo, we used endoscopic retrograde cholangiopancreatography (ERCP) adopting contrast substance (Fig. 3). Obtained image was taken for evaluation of current duct shape. Image Tool (Union D, USA) software was used for evaluation. Firstly, the image was imported in the software. After that, the calibration of image dimensions was performed and six lines were plotted.
Fig. 3: X-ray image of stenosed duct obtained using ERCP. 
The aim of measuring was evaluation of inlet and outlet radii, slope, and channel length. The model of channel with plotted lines is shown in Fig. 4. The measured parameters are presented in Tab. 1. It was obvious that stenosed duct may considered as tapered tube with finite length. Measured parameters were put in the geometrical model to evaluate the peristaltic flow in the duct with papillary stenosis.
Fig. 4: Model of stenosed duct with plotted lines. 
1. Parameters of stenosed duct. 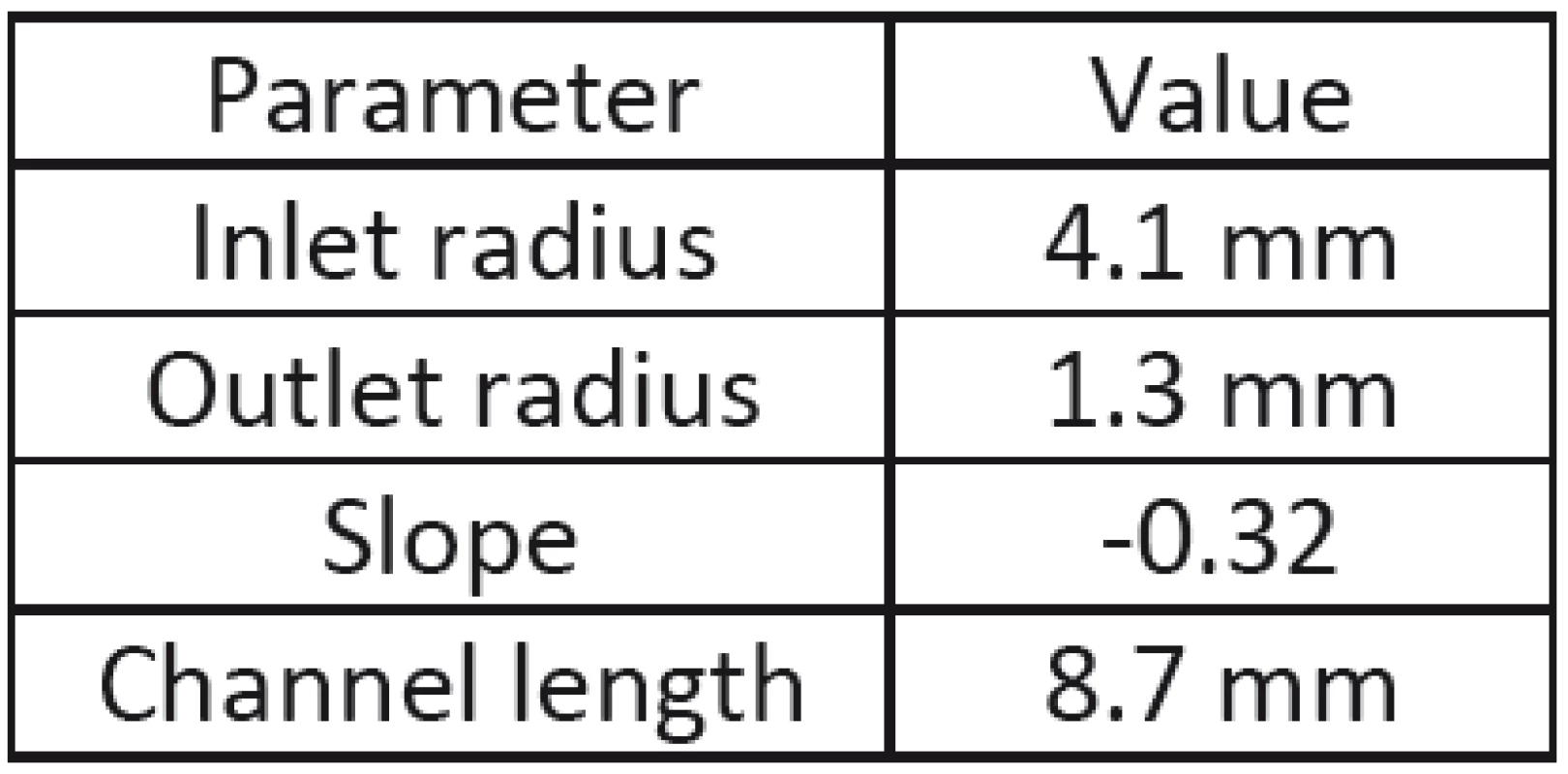
Mathematical modelling for peristaltic bile (as Carreau fluid) flow in tapered finite-length tube
We consider the peristaltic flow of a non-Newtonian fluid (Carreau fluid) in a tapered finite-length tube. Sinusoidal waves of constant speed propagate along the channel boundaries (Fig. 5). The wavelength is comparable with the channel length (L≈λ), thus the wave number is very small, and Reynolds number is negligible.
Boundary conditions are written as follows:
Fig. 5: Peristaltic flow in the tapered finite-length tube: problem sketch. 
The finite-length tube requires the pressures at two ends of the tube
In order to solve equations (1)–(3) and account for boundary conditions (4)–(9), the perturbation method is adopted and the solution is represented as an expansion over Weissenberg number (We):
where w0, w1, u0, u1, p0, p1 are solutions of zero and first order problems.
Zero order system solution
The axial and radial velocities as well as pressure difference can be found as follows:
where
First order system solution
The axial and radial velocities as well as pressure difference can be found as follows:
where
Velocity vectors at different time instants
Velocity vectors at different time instants of peristaltic wave propagation are plotted in Fig. 6 for We = 0.5 and φ = 0.1. The parameters were taken as follows: a = 0.006, λ = 0.5, l = 1, m = 0.56. Inlet and outlet pressures correspond to common bile duct pressure (1.12 kPa) and duodenum pressure (0.98 kPa) values [34]. Since the axisymmetric problem is considered, the velocities are plotted for the upper part of the tube only.
Fig. 6: Velocity vectors along the tube length at We = 0,5 and φ = 0.1 at different time instants: a - t = 0, b - t = 0.4, c - t = 0.8. 
Pressure versus flow rate
A relation between pressure drop and average flow rate under the effect of Weissenberg number and amplitude ratio is presented in Figs. 7, a–b. It is observed that the average flow rate grows up with an increasing magnitude of Weissenberg number and amplitude ratio. Weissenberg number strongly affects the pressure shift compared with the amplitude ratio. It should be noted that at = 0, the value of ∆p is maximal and after that the pressure gradient decreases when the flow rate increases.
Fig. 7: Dimensionless pressure difference vs. averaged flow rate: a is with variation of φ (φ = 0,1 [dash-dotted line], φ = 0,2 [dash line], φ = 0,3 [solid line]), b is with variation of We with variation of We (We = 0.1 [dash-dotted line], We = 0.5 [dash line], We = 0.9 [solid line]). ![Fig. 7: Dimensionless pressure difference vs. averaged flow rate: a is with variation of φ (φ = 0,1 [dash-dotted line], φ = 0,2 [dash line], φ = 0,3 [solid line]), b is with variation of We
with variation of We (We = 0.1 [dash-dotted line], We = 0.5 [dash line], We = 0.9 [solid line]).](https://pl-master.mdcdn.cz/media/image/84352f3eb75147c23cd5ebe33864140d.png?version=1537794987)
Moreover, it can be detected that at greater values of the pressure drop, the flow rate may have negative values that correspond to fluid flowing in the reverse direction (reflux) (condition Q < 0 is often regarded as reflux state). Thus, in our case the values of the pressure drop corresponding to Q = 0 may be called as choledochopancreatic reflux occurrence criteria.
Numerical simulation of peristaltic bile flow in tapered finite-length tube using ANSYS
To validate analytical model, we simulated peristaltic flow in the tapered tube using commercial package ANSYS Workbench (Canonsburg, USA).
Fig. 8: Velocity (a) and pressure distributions (b) at φ = 0.1. 
Fig. 9: Velocity (a) and pressure distributions (b) at φ = 0.3. 
The wall motion was controlled by a User Defined Function (UDF) where the midpoint was controlled by the function described in the UDF and is a sine function. The points on either side were prescribed by the function given in UDF and it is also a sine function.
The UDF was written in C code and put in the ANSYS Fluent to boundary conditions as moving wall.
The numerical validation showed good convergence with analytical model data.
Fig. 8–9 present velocity and pressure distributions at different values of φ=0.1 and 0.3.
Shape optimization of peristaltic Carreau fluid flow
For the proper stent installation, it is necessary to evaluate optimal values for inlet radius and slope to restore the flow rate in the healthy state. An average bile flow daily amount for a health adult person is approximately equal to 1500 ml [35]. Thus, it is necessary to formulate a shape optimization problem for the tapered finite-length tube at peristaltic Carreau fluid flow. Let us introduce objective function:
where Q is mean flow rate, Q* is an average bile flow daily amount.
The mean flow rate is defined as follows:
Varying inlet radius and slope (objective variables), let us minimize a deviation between Q and Q*. It corresponds to following problem solution by Nelder-Mead method:
It also should be noticed that the tube is need to be tapered anyway due to physiology. Nevertheless, we may control slope coefficient, but a limitation is that the tube can not be straight.
Results of optimization
The computed results for optimal parameters of slope coefficient and inlet radius are presented in Tab. 2. Velocity and pressure distributions for φ = 0,1 at different Weissenberg numbers (We = 0.1, We = 0.2, We = 0.3) The computed results showed that optimal parameters of the tapered tube at φ = 0,5 (for any Weissenberg number) and φ = 0,1 (for We = 0.1 and We = 0.2) provide rather glide flow. The results for velocities at φ = 0,1 and We = 0.1 and at φ = 0,1 We = 0.2 are approximately the same (Figs. 10, 12). The different velocity and pressure distribution may be observed at φ = 0,15 and We = 0.1 as well as φ = 0,1 and We = 0.3. In these cases, the optimum parameters of the tube are such that the outlet channel at certain time instants is almost closed. At the same time to provide the desired flow rate, the fluid rushes with higher velocities, which is accompanied by significant pressure fluctuations.
Fig. 10: Velocity distribution in the optimized tapered tube at We = 0.1 and φ = 0.1 at different time instants t = 0.4 (a), t = 0.8 (b), t = 1 (c). 
Fig. 11: Pressure distribution in the optimized tapered tube at We = 0.1 and φ = 0.1 at different time instants t = 0.4 (a), t = 0.8 (b), t = 1 (c). 
Fig. 12: Velocity distribution in the optimized tapered tube at We = 0.2 and φ = 0.1 at different time instants t = 0.4 (a), t = 0.8 (b), t = 1 (c). 
Fig. 13: Pressure distribution in the optimized tapered tube at We = 0.2 and φ = 0.1 at different time instants t = 0.4 (a), t = 0.8 (b), t = 1 (c). 
The pressure distributions for We = 0.1, We = 0.2, and We = 0.3 are shown in Figs. 11, 13, 15, respectively. It should be noticed that at first the pressure decreases slowly and finally rises sharply to meet the leading end of the bolus.
2. Optimal parameters of tapered tube at various Weissenberg number and amplitude ratio. 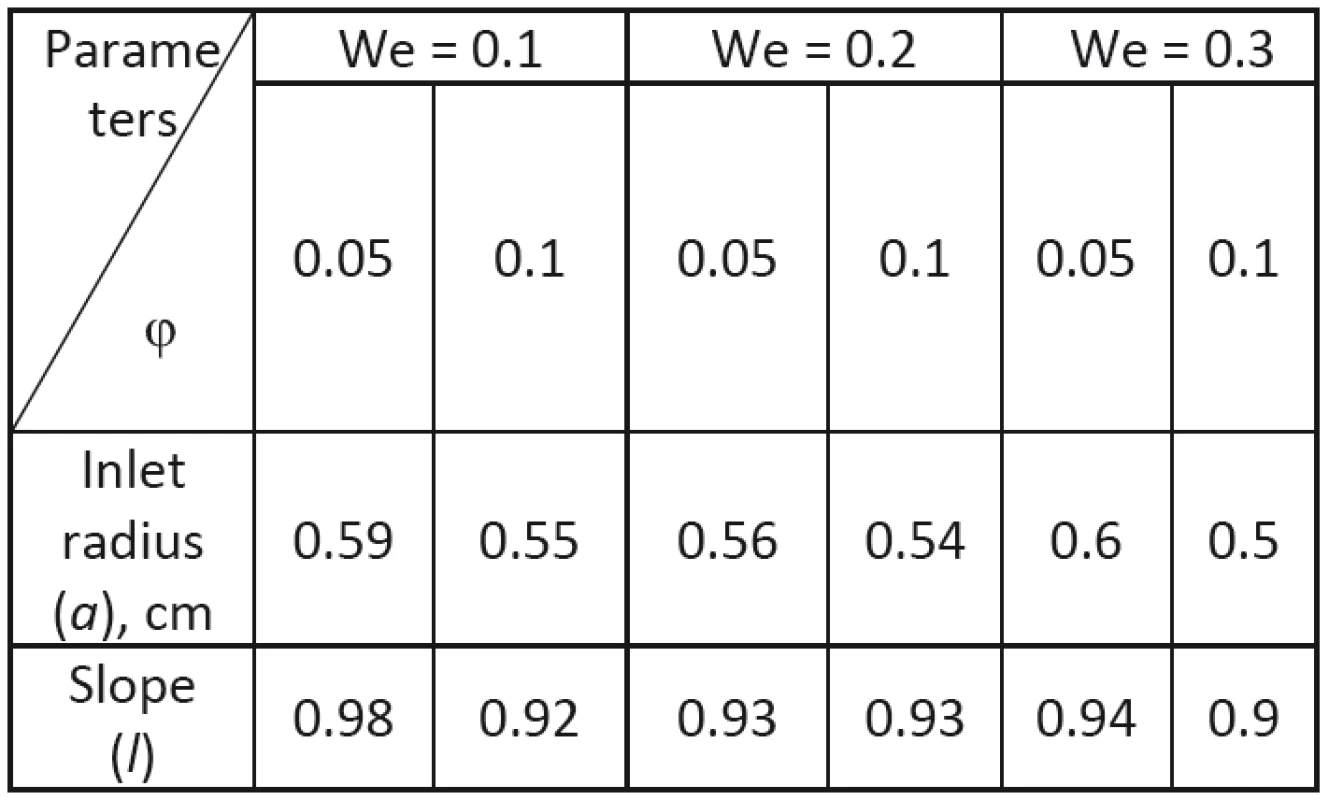
Fig. 14: Velocity distribution in the optimized tapered tube at We = 0.3 and φ = 0.1 at different time instants t = 0.4 (a), t = 0.8 (b), t = 1 (c). 
Thus, it should be noticed that peristaltic flow of Carreau fluid in the tapered finite-length tube is the mostly efficient at relatively low amplitude ratios of the peristaltic waves propagating along the Vateri’s papilla wall.
Fig. 15: Pressure distribution in the optimized tapered tube at We = 0.3 and φ = 0.1 at different time instants t = 0.4 (a), t = 0.8 (b), t = 1 (c). 
Conclusion
Papillary stenosis is a disease, which implies the narrowing of the Vateri’s papilla of making it like tapered tube. Peristalsis has an effect of the bile flow in that region. It should be noticed that peristaltic wave propagation and duct wall contraction is related to control signals from neural and endocrine systems.
A promising area of the research is to examine the sphincter modes at different stages of digestion and the providing of personal recommendations based on obtained results.Previously, it was shown that lithogenic bile can be regarded as non-Newtonian fluid. The flow of lithogenic bile as the Carreau fluid in the Vateri’s papilla modeled as a finite length tapered tube is discussed in the paper. Analytical solutions for axial and radial velocities and pressure difference are obtained. Pressure distribution versus axial coordinate at different time instants were plotted for various values of Weissenberg number and amplitude ratio. The values of the pressure gradient corresponding to reflux occurring are obtained. Moreover, it was shown that the pressure drop value corresponding to average flow rate Q = 0 may be called reflux occurrence criterion.
Numerical validation of peristalsis model is also presented. Computer modeling was performed in ANSYS Workbench. Velocity and pressure distributions showed good agreement between numerical and analytical data.
Moreover, shape optimization was performed using Nelder-Mead method. The aim of optimization was to obtain parameters of the tapered tube, which provide flow rate close to flow rate in the healthy state. Objective parameters were inlet radius and slope of duct wall. Influence of Weissenberg number on velocities and pressure drop in optimized tube geometries was also presented. The peristaltic flow is more efficient at low amplitude ratios.
The presented patient-specific approach can be implemented in the surgical practice during the planning of endobiliary interventions and stenting.
Acknowledgements
This work is supported by Russian Foundation for Basic Research, research project No. 16-08-00718 А. The work is partially supported by Russian Goverment Assignment (Project No. 19.7286.2017/8.9).
Alex Kuchumov, Ph.D.
Department of Theoretical Mechanics and Biomechanics
Faculty of Applied Mathematics and Mechanics
Perm National Research Polytechnic University
Komsomolskiy Prospect 29, 614990, Russia, Perm
E-mail: kychymov@inbox.ru
Phone: +7(342)237-17-02
Sources
[1] Maiti, S., Misra, J.C.: Peristaltic flow of a fluid in a porous channel: a study having relevance to flow of bile within ducts in a pathological state. International Journal of Engineering Science, 2011, vol. 49, no. 9, p. 950–966.
[2] Vahidi, B., Fatouraee, N.: A biomechanical simulation of ureteral flow during peristalsis using intraluminal morphometric data. Journal of Theoretical Biology, 2012, vol. 298, p. 42–50.
[3] Misra, M., Rao, A.R.: Peristaltic transport in a channel with a porous peripheral layer: model of a flow in gastrointestinal tract. Journal of Biomechanics, 2005, vol. 38, p. 779–789.
[4] Latham, T.W.: Fluid motion in a peristaltic pump. MS. Thesis, Massachusetts Institute of Technology, Cambridge, MA, 1966.
[5] Jaffrin, M.Y., Shapiro, A.H.: Peristaltic pumping. Annual Review of Fluid Mechanics, 1971, vol. 3, p. 13–35.
[6] Burns, J.C., Parkes, T.: Peristaltic motion. J. Fluid. Mech., 1967, vol. 29, no. 4, p. 731–743.
[7] Shapiro, A.H., Jaffrin, M.Y., Weinberg, S.L.: Peristaltic pumping with long wavelength at low Reynolds number. J. Fluid. Mech., 1969, vol. 37, p. 799–825.
[8] Fung, Y.C., Yih, C.S.: Peristaltic Transport. J. Appl. Mech., 1968, vol. 35, no. 4, p. 669–675.
[9] Eytan, O., Jaffa, A.J., Elad, D.: Peristaltic flow in a tapered channel: application to embryo transport within the uterine cavity. Med. Engng. Phy., 2001, vol. 23, p. 473–482.
[10] Jimenez-Lozano, J., Sen, M., Dunn, P.F.: Particle motion in unsteady two-dimensional peristaltic flow with application to the ureter. Phys. Rev. E., 2009, vol. 79, p. 041901-1–041901-15.
[11] Misra, J.C., Pandey, S.K.: Peristaltic transport of a non-Newtonian fluid with a peripheral layer. Int. J. Eng. Sci., 1999, vol. 37, p. 1841–1858.
[12] Misra, J.C., Pandey, S.K.: Peristaltic flow of a multi-layered power-law fluid through a cylindrical tube. Int. J. Eng. Sci., 2001, vol. 39, p. 387–402.
[13] Misra, J.C., Pandey, S.K.: Peristaltic transport of blood in small vessels: study of a mathematical model. Comput. Math. Appl., 2002, vol. 43, p. 1183–1193.
[14] Misra, J.C., Pandey, S.K.: Peristaltic transport of a particle-fluid suspension in a cylindrical tube. Comput. Math. Appl., 1994, vol. 28, p. 131–145.
[15] Misra, J.C., Pandey, S.K.: Peristaltic transport in a tapered tube. Math. Comput. Model., 1995, vol. 22, p. 137–151.
[16] Misra, J.C., Pandey, S.K.: A mathematical model for oesophegeal swallowing of a food-bolus. Math. Comput. Model., 2001, vol. 33, p. 997–1009.
[17] Usha, S., Rao, A.R.: Effect of curvature and inertia on the peristaltic transport in a two fluid system. Int. J. Engng. Sci., 2000, vol. 38, p. 1355–1375.
[18] Mishra M., Rao A.R.: Peristaltic transport of a Newtonian fluid in an asymmetric channel. ZAMP, 2003, vol. 54, p. 532–550.
[19] Rao, A.R., Mishra, M.: Peristaltic transport of a power law fluid in a porous tube. J. Non-Newtonian Fluid Mech., 2004, vol. 121, p. 163–174.
[20] Park, C.Y, Shur, M., Dewey, C.F.: A Study of fluid-membrane interactions that limit the output of peristaltic micropumps. J. Mech. Med. Biol., 2011, vol. 11, no. 2, p. 325–326.
[21] Kuchumov, A., Gilev, V., Popov, V., Samartsev, V., Gavrilov, V.: Non-Newtonian flow of pathological bile in the biliary system: experimental investigation and CFD simulations. Korea Australia Rheology Journal, 2014, vol. 26, no. 1, p. 81–90.
[22] Hakrem Abd, El., Naby Abd, El., Misery, A.E.M.El., Kareem, M.F.Abd El.: Separation in the flow through perisaltic motion of a Carreau fluid in uniform tube. Physica, 2004, vol. 343, p. 1–14.
[23] Nadeem, S., Riaz, A., Ellrhi, R., Akbar, N.S.: Series solution of unsteady peristaltic flow a Carrean fliud in eccentric cylinders. Ain shams Engineering Journal, 2013, vol. 27, p. 971–982.
[24] Mekheimer, Kh.S., Abdelmabond, Y., Abdellateef, A.I.: Peristaltic transport through an eccentric cylinders: mathematical model. Applied Bionics and Biomechanics, 2013, vol. 10, p. 19–27.
[25] Hayat, T., Saleem, N., Ali, N.: Peristaltic flow of Carreau fluid in a channel with different wave forms. Numerical Methods for partial differential equations, 2010, vol. 26, p. 519–534.
[26] Hariharan, P., Seshadri, V., Banerjee, R.K.: Peristaltic transport of non-Newtonian fluid in a diverging tube with different wave forms. Math. Comput. Model., 2008, vol. 48, p. 998–1017.
[27] Jian, C., Wang, G.: Biomechanical study of the bile duct system outside the liver. Biomed. Mater. Eng., 1991, vol. 1, no. 2, p. 105–113.
[28] Christopher, P., Armstrong, F.R.C.S., Taylor, T.V.: Pancreatic-duct reflux and acute gallstone pancreatitis. Ann. Surgery., 1986, vol. 15, p. 59–64.
[29] Allescher, H.D.: Papilla of Vater: structure and function. Endoscopy, 1989, vol. 21, p. 324–329.
[30] Zhang, Z.-H., Wu, S.-D., Wang, B. et al.: Sphincter of Oddi hypomotility and its relationship with duodenal-biliary reflux, plasma motilin and serum gastrin. World J. Gastroenterol., 2008, vol. 14, no. 25, p. 4077–4081.
[31] Kuchumov, A.G., Nyashin, Y.I., Samartsev, V.A.: Modelling of peristaltic bile flow in the papilla ampoule with stone and in the papillary stenosis case: application to reflux investigation. Proceedings of 7th WACBE World Congress on Bioengineering. Singapore, 2015, vol. 52, p. 158–161.
[32] Ballal, M.A., Sanford, P.A.: Physiology of the sphincter of Oddi – the present and the future. Part 2. The Saudi Journal of Gastroenterology, 2000, vol. 7, p. 16–21.
[33] Mallet-guy, P., Rose, J.: Pre-operative manometry and radiology in biliary tract disorders, Br. J. Surg., 1956, vol. 44, p. 128–136.
[34] Kuchumov, A.G., Nyashin, Y.I., Samarcev, V.A., Gavrilov, V.A., Mesnard, M.: Biomechanical approach to biliary system modelling as a step towards Virtual Physiological Human project. Russian Journal of Biomechanics, 2011, vol. 15, no. 2, p. 28–42.
[35] Adrian, T.: Motility and other disorders of the biliary tract. xPharm. The Comprehensive Pharmacology Reference, 2007, vol. 1, p. 1–6.
Labels
Biomedicine
Article was published inThe Clinician and Technology Journal

2017 Issue 2-
All articles in this issue
- PERISTALTIC FLOW OF LITHOGENIC BILE IN THE VATERI’S PAPILLA AS NON-NEWTONIAN FLUID IN THE FINITE-LENGTH TUBE: ANALYTICAL AND NUMERICAL RESULTS FOR REFLUX STUDY AND OPTIMIZATION
- /GD-TRACKER/ A SOFTWARE FOR BLOOD-BRAIN BARRIER PERMEABILITY ASSESSMENT
- EXPERIMENTAL ANALYSIS OF THE LUMBAR SPINE KINEMATICS
- RESPIRATORY SOUNDS AS A SOURCE OF INFORMATION IN ASTHMA DIAGNOSIS
- MEASUREMENT OF THE VALUES OF RADIOFREQUENCY ELECTROMAGNETIC FIELDS AROUND THE HEAD OF ADOLESCENTS
- The Clinician and Technology Journal
- Journal archive
- Current issue
- Online only
- About the journal
Most read in this issue- /GD-TRACKER/ A SOFTWARE FOR BLOOD-BRAIN BARRIER PERMEABILITY ASSESSMENT
- PERISTALTIC FLOW OF LITHOGENIC BILE IN THE VATERI’S PAPILLA AS NON-NEWTONIAN FLUID IN THE FINITE-LENGTH TUBE: ANALYTICAL AND NUMERICAL RESULTS FOR REFLUX STUDY AND OPTIMIZATION
- RESPIRATORY SOUNDS AS A SOURCE OF INFORMATION IN ASTHMA DIAGNOSIS
- MEASUREMENT OF THE VALUES OF RADIOFREQUENCY ELECTROMAGNETIC FIELDS AROUND THE HEAD OF ADOLESCENTS
Login#ADS_BOTTOM_SCRIPTS#Forgotten passwordEnter the email address that you registered with. We will send you instructions on how to set a new password.
- Career













